Угол наклона (крутизна ската) — это… Что такое Угол наклона (крутизна ската) в геодезии, определение

Уклон — Показатель крутизны склона; отношение превышения местности к горизонтальному протяжению, на котором оно наблюдается (например, уклон, равный 0,0I5, соответствует подъему I5 м на I 000 м расстояния).

Угол поворота трассы — Угол с вершиной, образованной продолжением направлений предыдущей стороны и направлением последующей стороны.

Уровенная поверхность — Во всех ее точках потенциал силы тяжести имеет одинаковое значение. Уровенная поверхность гравитационного поля Земли совпадает со средним уровнем воды Мирового океана.

Уравнивание — Совокупность математических операций, выполняемых для получения вероятнейшего значения геодезических координат точек земной поверхности и для оценки точности результатов измерений.

Уровень — Приспособление для проверки горизонтальности линий и поверхностей и измерения малых углов наклона. Основная часть — заполненная легкой жидкостью (за исключением небольшого объема «пузырька») стеклянная ампула.

Уклонение отвесных линий — Угол, образованный при несовпадении отвесной линии проведенной в точке на земной поверхности перпендикулярно геоиду с проведенной в этой же точке перпендикулярно к эллипсоиду нормалью.

Указатели склона — То же, что бергштрихи.

Универсальная программа обработки (спутниковых наблюдений) — Программа, позволяющая выполнять постобработку спутниковых определений, выполненных приемниками различных систем ГНСС, а также измерения выполненные другими системами (на­пример, системами лазерной локации спутников, системами длиннобазисной радиоинтерферометрии) (Bernes, GYPSY, GAMIT и др.).

Универсальный инструмент — Переносный угломерный инструмент для решения многих задач практической астрономии и геодезии, в частности для измерения координат (высот и азимутов) небесных светил и земных ориентиров.

как определить рекомендуемый угол ската и нагрузку

От того насколько правильно рассчитан угол наклона сооружаемой кровли зависит уровень надежности дома. В связи с этим при составлении проекта дома нельзя ориентироваться только на эстетические соображения. Особенности климата (большое количество снега зимой, сильный ветер) – это очень важный фактор при определении формы крыши. Универсальным считается значение наклона в пределах от 20 до 45º. Важно, что такой уклон позволяет использовать для изготовления крыш большинство кровельных материалов, которые предлагают современные производители.

Кроме того, следует знать, что определение оптимального уклона крыши невозможно без учета особенностей ее конструкции. Односкатная кровля является недорогой и простотой монтажа. Часто для формирования ее кровли используют профнастил. Так как чердака под такой крышей нет, особенно следует обратить внимание на создание системы вентиляции под такой кровлей.

Двускатные крыши с чердаками являются широко распространенными. Чердачное помещение под такой крышей позволяет осуществлять естественную вентиляцию. Возможно также обустройство чердака и создание под крышей жилого помещения. Уклон скатов крыши при этом – 11-45º. Значение угла наклона ската крыши обратно пропорционально значению нагрузок, которые возникают из-за действия дождя, снега и ветра. Чем большим будет наклон скатов, тем выше окажется парусность.

При устройстве вальмовых крыш, которые позволяют сооружать разнообразные крыши, скаты можно располагать под любым углом. За счет системы скатов кровельное покрытие в этом случае приобретает ломаную форму. В результате возможно сооружение мансардного этажа и жилого помещения в нем при проведении мероприятий по утеплению и пароизоляции крыши.

Особенности кровельного материала обязательно учитывают при проектировании и изготовлении крыши:

• Если применяется наборный штучный материал (например, натуральной черепицы), то минимальным считается угол более 22º.
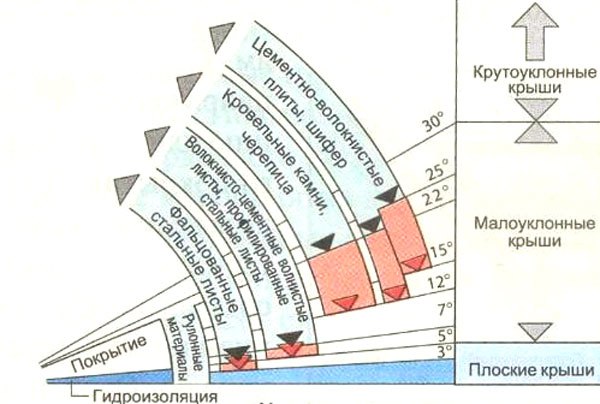
• Если используется рулонный материал, то угол наклона ската должен быть около 5º (трехслойное покрытие) или 15º (двухслойное покрытие).
• Профнастил рекомендуется укладывать на скате, наклон которого составляет 12º.
• При монтаже металлочерепицы наклона должен быть от 14º.
• Если для крыши в качестве кровельного покрытия используется ондулин, то наклон ската должен составлять 6º.

Угол наклона рельефа на местности: как измерить

Те пользователи, которые работают с рельефом в программе Наш Сад и используют для этого редактор Рельефа, знают: чтобы наклонить поверхность нужно задать угол ее наклона в градусах. Как же определить угол наклона рельефа подручными средствами, если в «кустах», случайно нет теодолита?

Метод вешек

Нам понадобятся: 3 колышка, шнур, рейка жесткая, уровень.
Вбиваем две вешки (колышка) по краям на перепаде высот (см. схему). Забиваем гвоздь или вкручиваем шуруп в произвольной точке С одной из вешек. Замеряем расстояние d от поверхности земли. Привязываем в этом месте шнур и с натяжением закрепляем его к другой вешке в точке А на том же, одинаковом расстоянии d от земли. Берем жесткую рейку, такую, чтобы не прогибалась и закрепляем на ней уровень. Устанавливаем рейку так, чтобы один ее конец находился в точке С, а другой лежал на еще одной вешке. Эту вешку забиваем в землю таким образом, чтобы она касалась натянутого шнура. Рейка на ней должна лежать горизонтально по уровню. Измеряем расстояние DE от шнура до рейки по вертикали и расстояние DС по горизонтали. Согласно схеме это длина рейки. Нам нужно найти значение угла β в градусах. Это и будет искомый угол наклона.


Мы легко можем измерить и вычислить соотношение DE/DC. В тригонометрии это тангенс угла – число, которое определяется соотношением противолежащего и прилежащего к этому углу катетов треугольника CDE. Зная это соотношение можно вычислить величину угла, например, воспользовавшись тригонометрической функцией, обратной тангенсу – арктангенсом.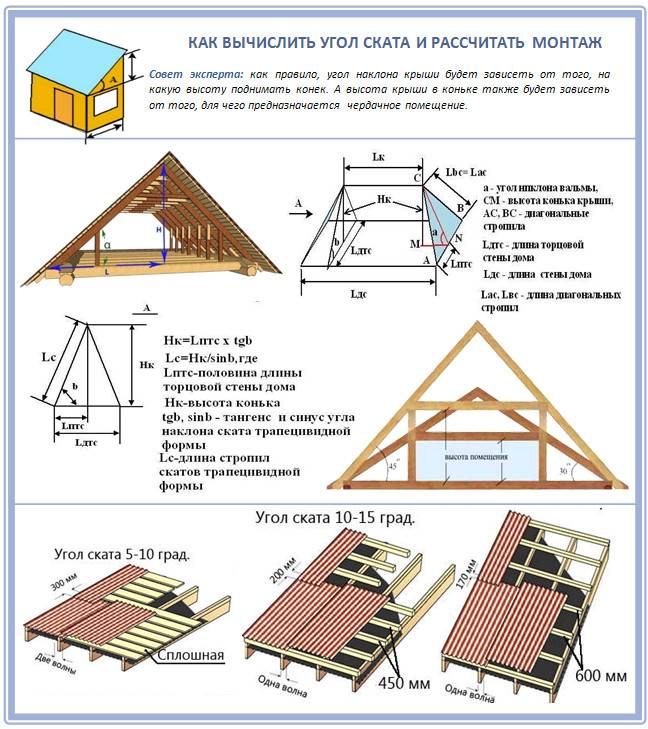

Вычисляем угол наклона на калькуляторе Windows

Значение арктангенса вычисляем, используя стандартный калькулятор из состава Windows. Щелкаем кнопку «Пуск», переходим в раздел «Все программы», находим «Стандартные» и жмем «Калькулятор». Этот же результат достигнем, нажав сочетание клавиш WIN + R, набрав в строке «Выполнить» команду calc и щелкнув кнопку «OK».
Переключаем калькулятор в режим вычисления тригонометрических функций. Для этого открываем меню «Вид» и находим пункт «Инженерный» или «Научный» (в зависимости от версии используемой операционной системы).
Вводим известное значение тангенса. Это делаем с клавиатуры или щелкая нужные кнопки интерфейса калькулятора.
При этом выбираем единицу измерения «Градусы» – DEG, чтобы получить результат вычисления именно в градусах, а не в радианах или градах. Ставим метку в checkbox (пустом квадратике) с надписью Inv. Так инвертируем значения вычисляемых функций, обозначенные на кнопках калькулятора. Если такого “квадратика” нет, зажимаем кнопку Shift или “↑”. На рисунке слева нужные нам параметры подчеркнуты красной линией.
Щелкаем кнопку с надписью tg или tan (тангенс) и далее « = ». Калькулятор вычисляет значение функции обратной тангенсу – арктангенс. Это значение и будет искомым углом.

Вместо Win-калькулятора можно использовать, например, онлайн-калькуляторы тригонометрических функций. Найти такие сервисы в интернете достаточно легко, задав поиск в браузере.

Важно помнить!

Измерения на местности проводим как можно точнее и рейку устанавливаем точно по уровню. Имейте в виду, что если длина рейки пусть даже полтора-два метра, а длина отрезка АВ метров 15-20, то даже незначительное отклонение уровня от горизонтали дает существенную погрешность. Тем не менее это разумный способ.  Он позволяет, пусть и не совсем точно, определить угол наклона рельефа местности.
Используя подобие треугольников АВС и СDЕ можно вычислить также перепад высот: h=АВ*DE/ DС.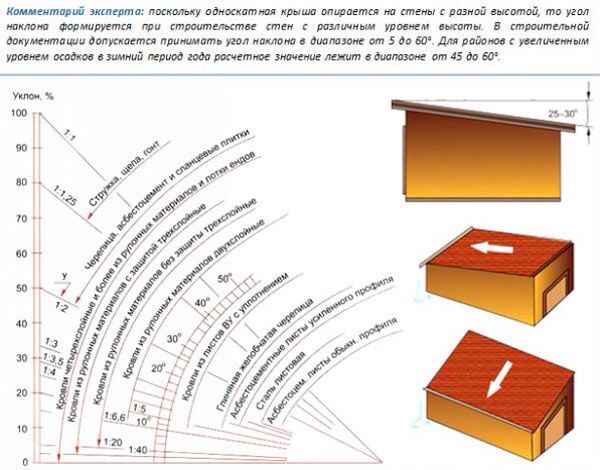

Расчёт угла наклона крыши

Поскольку от его величины зависит и количество кровельного материала, то выбор угла наклона и его предварительные расчеты производят до начала закупки выбранного кровельного материала.

Что на него влияет

В зависимости от величины уклона скатов крыши зависит особенность ее эксплуатации.

Принято выделять 4 типа крыш: высокие — с углом в 45–60 градусов; скатные — с наклоном от 30 до 45 градусов; пологие — с углом уклона 10–30 градусов; плоские — с углом 10 градусов и меньше.

На выбор величины этого параметра оказывают влияние, в первую очередь, природные факторы, которые характерны для данной местности.

Ветровая нагрузка

Сильный ветер самое большое давление оказывает на кровли высокие. Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы. И если вы решили устраивать именно высокую кровлю с очень большим уклоном, то следует позаботиться и об очень прочном основании. Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.

Нагрузка снеговая

Если в той местности, где строится дом, в холодное время года снегопад обильный, то следует строить кровлю с большим углом уклона. В этом случае высокая крыша вне конкуренции. На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.

). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах. Тем больший вес будет воздействовать на всю конструкцию. Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.

Выбираем уклон в зависимости от используемого кровельного материала

Прошли те времена, когда для покрытия использовали всего два вида кровельных материалов: черепицу и шифер. Каждый материал имеет свои индивидуальные технические характеристики и это при расчете необходимого значения угла наклона обязательно следует учитывать. Ведь может произойти так, что понравившийся вам материал по своим параметрам просто не подойдет.

Минимальный угол наклона

Существует понятие минимального значения этого параметра. Для каждого из материалов этот параметр свой. И если угол наклона, полученный в результате ваших расчетов, окажется меньше, чем минимальная величина для выбранного вами кровельного материала, то использовать его для устройства кровли нельзя.

В дальнейшем может возникнуть очень много проблем, если нарушить это правило:

• для любых штучных наборных кровельных материалов, таких как черепица или шифер, минимальная величина уклона составляет 22 градуса. Именно при таком значении на стыках не скапливается влага и внутрь крыши влага не просачивается;
• угол наклона для рулонных материалов (рубероид, бикрост и пр.) зависит от того, какое вы планируете укладывать количество слоев. Если три слоя, то уклон может составлять 2–5 градусов. Если же два слоя, то его требуется увеличить до 15 градусов;
• производители профнастила рекомендуют при устройстве кровли из этого материала устраивать угол уклона 12 градусов. Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком;
• для металлической черепицы значение этого параметра равняется 14;
• для ондулина — это величина в 6 градусов;
• минимальный уклон для мягкой черепицы равняется 11 градусам. 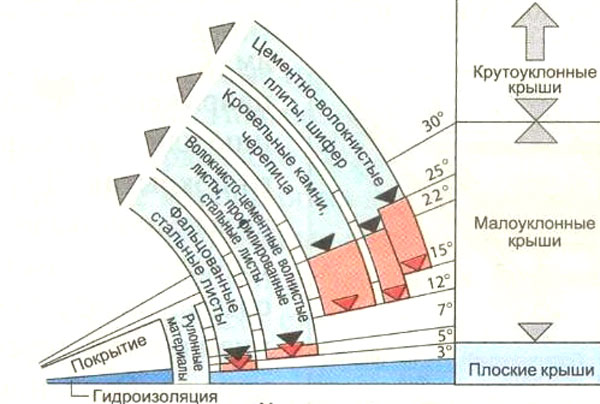Но при этом обязательное условие — сплошная обрешетка;
• для мембранных кровельных покрытий не существует жестких требований по минимальному значению этого параметра.

Это о минимальных величинах. Дадим совет — придерживайтесь этих правил, чтобы посреди зимы не пришлось всю кровлю перестилать.

Если в регионе дожди и снега случаются часто, то оптимальной будет крыша, угол наклона скатов у которой будет составлять 45 — 60 градусов. Ведь с кровли необходимо как можно скорее снимать нагрузку от воды и снега. Потому что прочность стропильной системы не беспредельна. А благодаря большому уклону кровли дождь и снег будут сходить максимально быстро.

Если в регионе, где построен дом, постоянно сильные ветра, то с крышей поступают иначе. При меньшем наклоне снижается ее парусность. И не возникает запредельных нагрузок на кровельный материал и стропила. Также не произойдет срывания крыши при резких порывах ветра. При этом оптимальный угол уклона кровли равняется 9–20 градусов.

Очень часто в регионе есть и снега, и ветер. Например, Оренбургская область. В таком случае выбирают среднее значение угла наклона. Как правило, его величина находится в диапазоне 20 — 45 градусов. Если вы обратите внимание, большинство скатных крыш имеют именно такое его значение.

Рассчитываем его величину

Для односкатной

Поскольку односкатная крыша опирается на стены, имеющие разную высоту, то формирование заданного угла наклона производят, просто поднимая одну из стен. Проводим вдоль стены перпендикуляр L сд, берущий свое начало в точке, где оканчивается короткая стена и опирающийся на стену, имеющую максимальную дину. В итоге образуется прямоугольный треугольник.

Для того, чтобы рассчитать длину стороны L bc, надо воспользоваться тригонометрической формулой.

Если длина стены L сд равняется 10 метрам, то, чтобы получить угол наклона 45 градусов, длина стены L bc должна ровняться 14.08 метра.

Для двускатной

Принцип расчета для двускатной крыши похож на предыдущий принцип.

Рассмотрим пример. Катет С — это половина ширины здания. Катет, а — это высота от перекрытия до конька. Гипотенуза является длиной ската. Если нам известны любые два параметра, то величину угла наклона можно легко рассчитать с использованием калькулятора.

Если ширина равна 8, а высота — 10 метров, то следует пользоваться формулой:
cos A = c+b

Ширина с = 8/2 = 4 метра.

В итоге формула выглядит так:

cos A = 4/10 = 0.4

По таблицам Брадиса находим значение угла, которому соответствует данная величина косинуса. Он равняется 66 градусов.

Для четырехскатной

И снова не обойтись без рулетки и таблиц Брадиса. Зная несколько параметров, можно без проблем вычислить другие. В том числе и угол наклона четырехскатной крыши. Следует помнить о том, что все размеры необходимо снимать максимально точно. А измерить уклон уже построенной крыши поможет специальный инструмент — уклономер. Ведь если вы ошибетесь, то углы наклона, длины и площади могут быть не верны. А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.

от чего зависит и как определить

Перед началом строительства необходимо тщательно и в мелочах продумать, как будет выглядеть будущий дом, а также каким функционалом он должен обладать. Одним из самых ответственных этапов являются расчеты кровельного покрытия. От того, какая форма крыши будет выбрана и какое помещение планируется непосредственно под ней, будет зависеть выбор материалов для кровли и определение угла наклона крыши. О том, как правильно рассчитать уклон кровли пойдет речь в этой статье.

Правильный расчет уклона кровли позволит не только определиться с необходимым количеством и типом материала, но и построить здание, соответствующее своему назначению. Оно будет теплым, влагонепроницаемым и крепким.

От каких параметров зависит уклон крыши?

Оптимальный уклон кровли выбирается с учетом многих факторов, основным из которых является воздействие погодных условий на кровельное покрытие. Рассмотрим три параметра, которые необходимо учитывать при выборе угла наклона кровли.

Ветер. Сильные ветра оказывают существенное давление на кровлю и постепенно могут ее разрушать. Для того чтобы снизить частоту ремонтов крыши или вовсе избежать их, необходимо, чтобы угол наклона крыши был небольшим. Чем меньше он будет, тем меньше парусности будет в крыше. Ей будет легче выдерживать порывы ветра. Остроконечные крыши, наоборот, берут на себя всю нагрузку, которую оказывает стихия. Они показали себя не практичными в тех местностях, где преобладают сильные ветра.

Если выбор сделан в пользу плоской крыши, необходимо помнить, что даже в такой кровле есть угол наклона. Он необходим для того, чтобы осадки могли скатываться к краю или к сливным отверстиям. В такой крыше минимальный уклон кровли может быть равен 1 градусу или 1,7%.

Осадки. В местности, где выпадает много осадков, рекомендуется сооружать крышу с углом наклона 45 градусов или выше, если речь идет о нижнем уровне мансардной крыше. Это позволит снегу скатываться с кровли. В противном случае снег накапливается на крыше и оказывает на нее дополнительную нагрузку. Из-за этого она может продавиться или же потерять свои гидроизоляционные свойства, когда снег начнет таять.

Материал кровли. Разные материалы обладают различным весом и свойствами. Например, покрытие из металлочерепицы может гнуться и отрываться, если подвергнуть его давлению ветра с торца. При выборе такого кровельного покрытия необходимо размещать скаты крыш в зависимости от преобладающего направления ветра так, чтобы он дул в покрытие кровли, а не в торец. Данное условие будет влиять и на угол наклона кровли, ведь ширина и длина дома могут быть разными. Кроме того, гладкие кровельные материалы позволяют осадкам беспрепятственно стекать с крыши, а те, которые имеют шершавую фактуру — задерживают их. Поэтому, если угол наклона кровли рассчитывается небольшим, то лучше выбрать более гладкие материалы, которые не будут скапливать на крыше дополнительный вес осадков. Существуют и другие параметры материалов, которые влияют на то, каким будет угол уклона кровли.

Угол уклона кровли в зависимости от материалов

Для кровли из металлочерепицы минимальный угол уклона будет составлять 15 градусов. При меньшем уклоне, влага начнет скапливаться, снижая срок службы крыши. Однако если угол наклона крови составляет 20 — 35 градусов, ей необходима усиленная гидроизоляция. Поскольку при таком уклоне снег может скапливаться на крыше.

Угол склона крыши из профнастила должен быть не менее 12 градусов, для мягкой кровли, гибкой черепицы, — 11 градусов, для материала на битумной основе — не менее 15 градусов. Черепичная или шиферная крыша будет тяжелой, поэтому очень важно правильно рассчитать систему стропил. А угол ее склона должен быть минимум 22 градусов. Эти данные соответствуют установленному ГОСТ образцу.

Как рассчитать угол уклона кровли?

Измерение склона кровли производится в градусах или процентах. Уклон плоской кровли имеет минимальный угол наклона 1 градус или 1,7 процента. Уклон остроконечной крыши может иметь, например, угол наклона 31 градус, тогда в процентном соотношении ее склон будет составлять 60 процентов. Максимальный угол наклона составляет 45 градусов и это равняется 100 процентам. Для того чтобы быстро определить показатели в процентах и градусах используют специальные таблицы. Измерение в градусах представляет собой определение угла, который образуется между плоским основанием и кровельным перекрытием. Уклон кровли в процентах часто используется в строительных чертежах.

Вычисления угла наклона можно произвести несколькими несложными способами. Если представить крышу в форме треугольника, то высота конька и основание крыши — это катеты, а скат кровли — гипотенуза. Необходимо определить угол между гипотенузой и одним из катетов — основанием крыши. Для этого необходимо разделить высоту конька на ширину второго катета. Ею в двухскатной крыше является величина, равная половине ширине дома. Полученное значение умножается на 100 и, таким образом переводится в проценты.

Сделаем для примера расчет угла склона двухскатной крыши при высоте конька 3 метра:

• высота конька 3 метра, катет равен 3 метрам.

• ширина дома 20 метров, катет равен 20/2 метра.

3/10=0,3

Коэффициент равен 0,3, что соответствует 30%. Угол наклона кровли равен примерно 22 градуса.

Также угол наклона кровли можно рассчитать с помощью электронных калькуляторов для расчета ската крыши, в которые задаются параметры высоты конька и ширины здания. В таком случае можно поучить не только коэффициент угла, но и расчеты стропил. Также можно использовать угломер,

инструмент, который безошибочно определяет нужный угол кровли в градусах или процентах непосредственно на месте строительства.

Чтобы достичь заданного угла наклона кровли можно менять высоту конька крыши или ее форму. В случае, если выбрана мансардная форма крыши, расчет уклона кровли производится обычным способом, но для этого необходимо разбить зоны крыши на треугольники и просчитать угол наклона для каждого в отдельности.

Факторы, которые определяют угол наклона кровли

Для того чтобы вывести идеальный угол наклона крыши, необходимо учесть несколько важных факторов. Среди них такие:

1. Климатические условия.

2. Функциональность помещения под крышей.

3. Используемый материал.

4. То, какую нагрузку способен выдерживать фундамент и строение в целом.

5. Экономичность.

6. Энергоэффективность.

Климат, который преобладает в месте постройки дома, является определяющим фактором, он играет одну основную роль в выборе формы и угла наклона крови. В местности с сильными ветрами рекомендуется устанавливать крыши с небольшим углом наклона. Но, в то же время, на такой крыше в большем объеме собираются осадки. Поэтому на территории с сильными ветрами и большим количеством осадков необходимо конструировать крышу с оптимальным углом наклона. Он будет индивидуальным для каждого конкретного дома.

После определения угла наклона кровли, необходимо решить, какой материал будет самым подходящим. Каждое покрытие имеет разный вес. Тяжелые кровельные материалы требуют запаса прочности фундамента и строения в целом, усиленной стропильной конструкции. Это в свою очередь сделает конструирование крыши более дорогостоящим. С учетом всех этих факторов определяется идеальный угол наклона кровли для каждого конкретного дома.

Однако, если откинуть прагматичную сторону вопроса, то на первый план выходит задумка застройщика и его намерения относительно эксплуатации помещения под крышей.

Если планируется построить дом с жилым мансардным этажом, то, чтобы определить, как правильно рассчитать наклон крыши, необходимо учесть требования к материалу кровли, его тепло- и гидроизоляции. Эти критерии встанут на первое место, а вопрос экономичности и соответствия климату — на второе. Также стоит отметить, что строительство дома с мансардным этажом будет более экономичным, чем строительство двухэтажного дома. Поэтому такое решение является достаточно популярным. Мансардный этаж — это полноценное жилое пространство, которое в определенных случаях является единственной альтернативой для создания нужного жилого пространства. Мансардный этаж не требует возведения стен и, соответственно, дополнительного запаса прочности для фундамента.

Профессиональный подход в конструировании кровли

Необходимый угол наклона кровли может моделироваться за счет изменения высоты конька, а также с учетом всех факторов для создания долговечного и комфортного дома. Чтобы грамотно определить уклон кровли, как того требуют стандарты качества, необходимо учесть все нюансы в расчетах и возведении кровли. Поэтому это дело нужно доверить профессионалам. Однако каждый дом начинается с бумаги. Благодаря необходимым знаниям и нехитрым расчетам, будущий застройщик может строить реалистичные и подходящие для него наброски своего будущего дома.

Видео

Добавить комментарий

Датчик угла наклона — Миэлта Технологии

Устройство предназначено для определения положения в пространстве и измерения углов отклонения как абсолютных, так и дифференциальных. Используется для контроля работы различных механизмов в автомобильной и сельхозтехнике.

Датчик угла наклона Mielta имеет несколько алгоритмов работы, что увеличивает сферу применения устройства: возможность работы с относительным углом наклона и в трехмерной системе координат.

• Специализированный алгоритм сглаживания данных дает более удобные для чтения данные.
• Корпус, отвечающий высоким требованиям по прочности и металл рукав длиной 1,5 м, дают возможность использовать датчик в зонах повышенной опасности.

• Характеристики

Напряжение питания	10 — 36 В
Потребляемый ток	40 мА
Измеряемые углы	0 — 180°
Интервал обновления данных	1 – 30 с
Частотный выход	500 – 680 Гц
Разрешение	1°/Гц
Дискретность	1°
Нагрузка на частотный выход (max)	+10/-100 мА
Скорость RS485	9600 бит/с
Протокол	Modbus
Нагрузка на дискретные выходы	-100 мА
Температура эксплуатации	-40 — +50 °С
Степень защиты	IP66
Вес	150 г

КОНФИГУРАТОР

Угол наклона крыши для металлочерепицы: как рассчитать оптимальный?

09. 01.2020

Уклон кровли – это угол, который образуют кровельный скат и плоскость перекрытий. Угол наклона крыши из металлочерепицы зависит от многих параметров. К примеру, производитель Компания Металл Профиль прямо указывает в инструкции, какой именно уклон рекомендован для того или иного профиля черепицы. В целом диапазон, в котором может находиться угол кровельного ската из металлочерепицы, довольно велик – от 12 до 90 градусов. Однако специалисты по монтажу указывают 22 градуса, как оптимальный угол. Если по каким-то причинам вы хотите сделать кровлю более крутой или более пологой, примите во внимание некоторые особенности того и другого вариантов.

Малый уклон

• Слишком малый наклон кровли затруднит использование мансардного пространства.
• Чем меньше угол ската, тем хуже с неё стекает вода и тем больше снега скапливается на кровле.
• Более пологая кровля даёт больше нагрузки на стропильную систему. В таком случае целесообразно изготавливать её из более толстых пиломатериалов или же уменьшать шаг между элементами.

Большой уклон

• Слишком большой уклон затруднит выход на крышу, её обслуживание и ремонт.
• С повышением угла ската увеличится и его площадь, а, следовательно, количество необходимых стройматериалов: металлочерепицы, древесины для обрешётки, гидро- и теплоизоляции. Также вырастет вес кровельного пирога в целом и стоимость работ по монтажу кровли.

Вычислить лучший угол наклона кровли из металлочерепицы лучше всего на этапе проектирования дома, чтобы адекватно рассчитать нагрузку на фундамент. При этом необходимо учесть ряд критериев.

Снеговая нагрузка

Чем больше снега выпадает в вашем регионе, тем круче должен быть минимальный уклон крыши из металлочерепицы. Ошибка может стоить вам обрушения всей стропильной конструкции, не выдержавшей снеговую массу.

Ветровая нагрузка

И напротив, наклон крыши для металлочерепицы желательно сделать минимальным в том случае, если сильные ветра и ураганы в регионе не редкость. Такая структура уменьшит парусность крыши.

Тип кровли

На выбор угла ската влияет также тип будущей кровли. Односкатной крыше достаточно 20-30 градусов, двускатную можно сделать покруче, с углом 20-45 градусов.
Таким образом, мы видим, что нельзя однозначно ответить на вопрос: какой минимальный угол наклона крыши для металлочерепицы? Довольно много параметров нужно учесть, чтобы получить надёжную и практичную кровлю. Поэтому лучше решение этой задачи доверить профессионалам.

Найдите оптимальный угол для установки солнечных панелей

Угол наклона и азимута: на какой угол мне наклонить солнечные панели?

«Угол наклона» или «угол возвышения» описывает вертикальный угол ваших солнечных панелей. «Азимутальный угол» — это их горизонтальная ориентация по отношению к экватору.

Солнечные панели должны быть направлены прямо на солнце, чтобы оптимизировать их мощность. В этой статье объясняется, как найти правильный угол наклона и азимута, чтобы получить максимальную производительность от вашего массива.

Добро пожаловать в очередной выпуск нашей продолжающейся серии Solar 101. Сегодня мы собираемся объяснить, как установить солнечные панели, чтобы получать от них максимум энергии.

Начнем с двух ключевых терминов: угол места и азимутальный угол (для краткости обычно сокращается до «угол» и «азимут»).

• Угол подъема: вертикальный наклон панелей.
• Азимутальный угол: горизонтальная ориентация панелей (в данном случае по отношению к экватору).

Солнечные панели работают лучше всего, когда они обращены прямо на солнце. Но эта задача усложняется тем, что солнце движется по небу в течение дня. Он также меняет угол в небе при смене времен года.

Итак, когда вы строите солнечную систему, возникает вопрос: под каким углом лучше всего устанавливать солнечные панели, чтобы получить максимальную отдачу?

Угол наклона и азимута относительно экватора.

Некоторые люди захотят установить его под одним углом и забыть об этом, в то время как другим нравится работать со своей системой и вносить коррективы для оптимизации вывода.

Вы также можете купить трекер, который автоматически отслеживает положение солнца в небе, чтобы получить максимальную отдачу от ваших панелей. Но трекеры редко бывают самым экономичным вариантом. Почти всегда дешевле купить еще несколько панелей, чем вкладывать деньги в трекер.

Оптимальный азимутальный угол для солнечных панелей

Для достижения наилучших результатов ваши солнечные панели должны быть обращены к экватору. Если вы живете в Северном полушарии, поверните их лицом на юг. Если вы живете в Южном полушарии, смотрите им на север.

(Поскольку мы американская компания, в следующем примере предполагается, что вы наведете свою систему на юг.)

В частности, вы должны направить панели на истинный юг , а не на показания компаса, которые магнитный юг .

Многие люди удивляются, узнав, что их компас не совсем точен. Это происходит потому, что магнитные силы в ядре Земли уводят стрелку компаса от истинного севера или истинного юга. В зависимости от вашего местоположения показания компаса могут быть неточными на целых 25 °!

FREE Solar Racking Guide

Разница между магнитным севером (показанием компаса) и истинным севером называется магнитным склонением.Это измерение того, сколько градусов вам нужно компенсировать по показаниям компаса, чтобы найти истинный север.

Положительное число представляет собой восточное склонение, то есть истинный север находится к востоку от показаний компаса. Отрицательное число представляет западное склонение, то есть истинный север находится к западу от показаний компаса.

Так как же рассчитать идеальный азимутальный угол для ваших панелей?

Сначала найдите свое магнитное склонение по одной из множества онлайн-карт или с помощью такого инструмента, как NOAA.калькулятор правительства.

Отрегулируйте облицовку панелей по значению магнитного склонения в вашем местоположении. Направление, в котором вы настраиваете панели, зависит от того, где вы живете:

В Северном полушарии:

• Если ваше магнитное склонение восточное (положительное), поверните панели на восток.
• Если ваше магнитное склонение западное (отрицательное), поверните панели на запад.

В Южном полушарии:

• Если ваше магнитное склонение восточное (положительное), поверните панели на запад.
• Если ваше магнитное склонение западное (отрицательное), поверните панели на восток.

Два примера, демонстрирующие разницу:

Если вы живете в Сан-Диего, Калифорния, ваше магнитное склонение составляет примерно 11 ° восточной долготы. Так как Сан-Диего находится в Северном полушарии, начните с поиска магнитного юга, затем отрегулируйте на 11 ° на восток .

Для сравнения: Кокран, Чили также имеет магнитное склонение около 11 ° восточной долготы. Но поскольку вы находитесь в Южном полушарии, вместо этого вы хотите направить свои панели на север.Таким образом, вы фактически должны отрегулировать на 11 ° на запад , чтобы найти идеальный азимут.

Выполняя эти настройки, вы будете обращены к своим панелям прямо на экватор, максимально увеличивая их воздействие солнечного света (и, соответственно, количество вырабатываемой солнечной энергии).

Поиск оптимального наклона для ваших солнечных панелей

Другая половина уравнения — это определение вертикального угла или наклона ваших солнечных панелей.

У вас есть несколько вариантов: выбрать один угол и оставить его в покое или отрегулировать наклон несколько раз в год для оптимизации сезонного производства.

В зависимости от ваших предпочтений, вот наш совет.

Оптимальный угол наклона (без регулировки)

Если вы никогда не хотите утруждать себя настройкой панелей, установите их под углом наклона, равным вашей широте.

Чтобы снова использовать приведенный выше пример, Сан-Диего расположен на широте 32,7157 ° северной широты. Вы будете в порядке, если установите панели под углом 33 ° и не трогаете их.

Одна деталь, которую следует учитывать, — это немного изменить угол наклона в пользу летнего или зимнего режима работы.Если вы тратите больше денег на работу кондиционера летом, возможно, вы захотите оптимизировать его для летнего производства. С другой стороны, если вы в конечном итоге излучаете жару во время суровых зим, вы можете настроить свои панели на зимнее производство.

Это имеет большее значение для автономных систем, поскольку вы храните собственную энергию. Если вы привязаны к сети, вы, скорее всего, захотите оптимизировать производство в летний период, поскольку коммунальная компания обычно дает вам кредит за любое перепроизводство. Летом вы будете производить больше, а в зимние месяцы можете получить в счет этого кредита.

Чтобы оптимизировать производство в целом в течение всего года, наклоняйте панели по своему усмотрению.

Чтобы увеличить производство летом, наклоните панели на вашу широту минус 10-15 ° .

Чтобы увеличить производительность зимой, наклоните панели на вашу широту плюс 10-15 ° .

Сезонная корректировка оптимального угла наклона

Если у вас есть регулируемое крепление и вы не против наклонять панели вручную, вы можете изменять угол несколько раз в год, чтобы увеличить производительность вашего массива.

Следует отметить, что это не особо распространенный выбор. Большинство наших клиентов просто обеспечивают себе 5-10% -ную амортизацию при выборе размера своей системы, поэтому им никогда не нужно вносить какие-либо изменения.

Основное исключение — участки с сильным снегом. Если на панелях будет скапливаться снег, целесообразно установить опоры на столб. Вы можете настроить их на более крутой угол наклона зимой, что не только улучшает производительность, но и сбрасывает снег с лицевой стороны панелей.

Сопутствующий продукт: General Specialties 10x Pole Mount

Если вы можете регулировать угол наклона солнечных панелей несколько раз в год, вот график регулировки, который мы рекомендуем:

• Пружина: наклоните панели на ваша широта .
• Лето: Наклоните панели на своей широты минус 15 ° .
• Падение: Наклоните панели на своей широты .
• Зима: Наклоните панели на своей широты плюс 15 ° .

Это общие рекомендации, но вы можете получить лучшие результаты, настроив график корректировок в зависимости от вашего местоположения. Для получения дополнительной информации прочитайте solarpaneltilt.com, старый, но все еще отличный справочник, в котором объясняется (очень подробно), как наклонять панели, чтобы максимизировать их производительность.

Примечание о трекерах

Трекеры автоматически настраивают вашу систему так, чтобы ваши панели всегда были обращены прямо на солнце. Идея состоит в том, чтобы выжать из ваших панелей как можно больше продукции.

Хотя идея прекрасно звучит в теории, трекеры редко имеют смысл в жилых системах. Оборудование для слежения стоит 600–1000 долларов за панель, и можно ожидать, что эти вложения принесут вам от 60 до 90 Вт дополнительной мощности на панели мощностью 300 Вт.

В качестве альтернативы, если вам нужно больше мощности, вы можете просто добавить еще одну панель на 300 Вт примерно за 160 долларов.Если у вас есть место, гораздо дешевле добавить больше панелей.

В коммерческих системах математика меняется, но в целом большинству людей трекеры не нужны. Прочтите полное объяснение здесь.

В конце концов, вам не нужно беспокоиться о тонкой настройке вашей системы, если только вам не грозит нехватка места для ее сборки. Трекеры часто бывают слишком дорогими, и, честно говоря, настройка панелей будет казаться утомительной, если вам не нравится практический подход DIY.

Если у вас много места, мы рекомендуем создать себе подушку, добавив несколько дополнительных панелей.Удобство того стоит.

Для получения дополнительной информации ознакомьтесь с нашим бесплатным руководством по стеллажам для солнечных батарей.

Самый быстрый словарь в мире: Vocabulary.com

Угол наклона: угол, под которым ракета изгибается по своей траектории относительно вертикали

телесный угол угол, образованный тремя или более плоскостями, пересекающимися в общей точке (вершине)

прерывисто, неустойчиво

прерывисто-прерывисто

красноречиво красноречиво

острый угол угол менее 90 градусов, но более 0 градусов

прямоугольник параллелограмм с четырьмя прямыми углами

под прямым углом Угол в 90 градусов между двумя перпендикулярными линиями

треугольник трехсторонний многоугольник

распутать разделить скрученную массу

пренебрежительно пренебрежительно

вводит в заблуждение вводящим в заблуждение способом

золотой орел большой орел горных районов северного полушария с золотисто-коричневой головой и шеей

умоляюще-умоляюще

усердно, неуклюже

прямоугольный треугольник треугольник с одним прямым углом

злорадно злорадно

покорно послушно

запутывание причина скручивания или захвата скрученной массы

задушить убить, сдавив горло так, чтобы отрезать воздух

как рассчитать угол наклона солнечной панели?

Узнайте, как рассчитать оптимальный угол для солнечной панели для вашей солнечной системы в зависимости от вашего местоположения и сезона.Объяснение двух методов расчета.

Как рассчитать угол наклона солнечной панели вашей солнечной системы?

Угол наклона солнечной панели вашей солнечной системы зависит от того, в какой части мира вы находитесь. Панели солнечных батарей дают максимальную выходную мощность, когда они обращены прямо к солнцу . Солнце движется по небу и может быть низким или высоким в зависимости от времени дня и сезона. По этой причине идеальный угол никогда не фиксируется. Чтобы в течение дня на панель попадало как можно больше солнечного света, необходимо определить, в каком направлении панели должны быть обращены, и рассчитать оптимальный угол наклона.Это будет зависеть от:

• Где вы живете
• В какое время года вам нужно больше всего солнечной энергии

Угол наклона солнечной панели

Расчет оптимального угла наклона солнечной панели

Как показывает практика, солнечные панели должны быть более вертикальными зимой, чтобы получать большую часть низкого зимнего солнца, и более наклонными летом , чтобы максимизировать мощность. Вот два простых метода расчета приблизительного угла наклона солнечной панели в зависимости от вашей широты.

Метод расчета один

Оптимальный угол наклона рассчитывается следующим образом: прибавляет 15 градусов к вашей широте зимой и вычитает 15 градусов от вашей широты летом. Например, если ваша широта составляет 34 °, оптимальный угол наклона солнечных панелей зимой будет 34 + 15 = 49 °. С другой стороны, оптимальный угол наклона летом будет 34-15 = 19 °.

Метод расчета два

Это улучшение общего метода, дающее лучшие результаты.В этом методе оптимальный угол наклона солнечных панелей в зимний период рассчитывается путем умножения широты на 0,9 и последующего добавления 29 °. В приведенном выше примере широты 34 ° угол наклона будет (34 * 0,9) + 29 = 59,6 °. Этот угол на 10 ° круче, чем в обычном методе, но очень эффективен при отражении полуденного солнца, которое является самым жарким в короткие зимние дни. Для лета угол наклона рассчитывается путем умножения широты на 0,9 и вычитания 23,5 °. В приведенном выше примере этот угол будет (34 * 0.9) — 23,5 = 7,1 °. Для получения оптимальных углов наклона весной и осенью из широты вычитается 2,5 °.

Как вы его нашли — и имеет ли это значение?

В этом сообщении блога мы исследуем, что означает изменение положения солнца для производства солнечной энергии, а также как можно расположить панели для максимальной производительности. Мы также объясним, как лучший угол наклона солнечной панели зависит от различных факторов. Наконец, мы исследуем, насколько на самом деле важно достичь оптимального угла.

Но прежде чем мы начнем, небольшое примечание: угол наклона солнечной панели также известен как наклон солнечной панели.Вы увидите, что термины используются как взаимозаменяемые как в этой статье, так и в Интернете.

Что означает «угол наклона солнечной панели»?

Угол наклона солнечной панели — это еще один способ описания вертикального наклона вашей фотоэлектрической системы. Когда солнечная система находится на уровне земли, у нее нет наклона. Если он стоит вертикально — перпендикулярно земле — он находится под углом 90 °.

Угол наклона панели солнечных батарей может влиять на количество вырабатываемой солнечной энергии и зависит от двух факторов: широты и времени года.

Оптимизация и регулировка наклона вашей солнечной панели в соответствии с этими факторами может помочь вам максимизировать производство солнечной энергии.

Какой угол наклона солнечной панели лучше всего подходит для вашей широты?

Угол наклона увеличивается с широтой — чем дальше ваш дом от экватора, тем выше должен быть угол наклона.

Например, в штатах, расположенных на более низких широтах (таких как Аризона и Гавайи), солнце находится выше в небе. В этих состояниях солнечные фотоэлектрические панели требуют небольшого наклона для улавливания прямых солнечных лучей.

Напротив, для штатов в более высоких широтах, таких как Миннесота и Орегон, солнце находится ниже в небе. В этих штатах солнечные фотоэлектрические панели следует устанавливать под большими углами наклона, чтобы получать максимальное количество солнечного света.

Наклон солнечной панели зависит от положения солнца. Изображение предоставлено EIA

Оптимальный угол наклона увеличивается с увеличением широты. Источник изображения: EIA

Как определить оптимальный угол наклона солнечных панелей для вашего штата?

Существует простое практическое правило для расчета наилучшего угла наклона для стационарных солнечных панелей.Вычтите 15 градусов из широты вашего местоположения летом и добавьте 15 градусов к своей широте зимой.

Чтобы получить точный метод, используйте вторую формулу на этой странице для вычисления угла наклона.

Например, в районе залива Сан-Франциско лучший угол наклона солнечной панели составляет 22–23 градуса. Для Лос-Анджелеса лучше всего подходит наклон панели солнечных батарей на 19 градусов.

Эти углы обеспечат наилучшую общую производительность в течение года, если вы собираетесь использовать фиксированную установку.На самом деле возможно увеличить производство энергии, отрегулировав солнечные панели в зависимости от сезона — мы объясним это в следующем разделе.

Рассчитайте, сколько будут стоить солнечные панели для вашего дома в зависимости от вашего местоположения

Какой угол наклона солнечной панели лучше всего подходит для каждого сезона?

Угол наклона солнца меняется не только в зависимости от широты, но и от времени года. Как показано на рисунке ниже, солнце ниже в зимние месяцы и выше в летние.

Это означает, что если вы хотите, чтобы ваши солнечные панели всегда располагались для максимального воздействия солнечного света, вам необходимо настраивать их для каждого сезона.

В таблице ниже показан оптимальный угол наклона солнечной панели для различных штатов США зимой, весной / осенью и летом.

Оптимальные углы наклона солнечных панелей для различных городов США

Государство	Город	Зима	Весна / Осень	Лето
Калифорния	LA	32 °	56 °	80 °
Нью-Йорк	Нью-Йорк	26 °	49 °	72 °
Аризона	Тусон	34 °	58 °	82 °
Флорида	Майами	40 °	64 °	88 °
Техас	Даллас	34 °	57 °	80 °
Нью-Джерси	Атлантик-Сити	28 °	51 °	74 °
Коннектикут	Гринвич	26 °	49 °	72 °
Вирджиния	Ричмонд	30 °	53 °	76 °
Мичиган	Редфорд	24 °	48 °	72 °

Система на 40 ° широты имеет значительный прирост энергии в 4 раза.1% при корректировке всего два раза в год.

Две дополнительные корректировки для весны и осени могут дать дополнительный выход 0,5% — см. Ниже.

Как изменение угла влияет на мощность солнечной панели

	Стационарная установка	Скорректировано на 2 сезона	Скорректировано 4 сезона
Выход в% от оптимума	71,1%	75.2%	75,7% *

Однако регулировка солнечных панелей четыре раза в год (или даже два раза) — непростая задача. В конце концов, большинство солнечных панелей устанавливаются под фиксированным углом крыши и не могут быть отрегулированы.

Единственный способ легко настроить солнечные панели — это использовать наземную систему и установить солнечные панели с отслеживанием оси. Однако у этого подхода есть большой недостаток: хотя он и увеличивает мощность солнечной энергии, он значительно увеличивает ваши расходы.В результате, трекеры солнечной оси в настоящее время не стоят вложений.

* Вам интересно, почему вы все еще получаете только 75,7% оптимальной производительности после корректировки для каждого сезона? Это потому, что оставшаяся сумма может быть достигнута только путем корректировки направления солнечной батареи в течение дня. Мы расскажем о направлении солнечных панелей в следующем блоге.

Каким образом пологая или крутая крыша влияет на выработку солнечной энергии?

Если вы сравните мощность, производимую солнечными панелями за год, вы обнаружите, что существует относительно небольшая разница между панелями, установленными на неглубокой (15 градусов) крыше и крутой (45 градусов) крыше.

Это потому, что разные поля будут сбалансированы в зависимости от сезона. Солнечные панели на неглубокой крыше улавливают больше солнечного света в летний сезон, тогда как солнечные панели на крутой крыше будут производить больше энергии зимой.

Несмотря на то, что вы можете использовать трекеры солнечных панелей, чтобы держать их под оптимальным углом в любое время, затраты и связанные с этим сложности в большинстве случаев не окупаются.

Таким образом, в штатах, благоприятных для использования солнечной энергии, таких как Калифорния, большинство домовладельцев считают, что солнечные системы стоят вложений, независимо от угла, под которым они установлены.

Об этом свидетельствует статистика солнечной энергии Калифорнии, как показано ниже на этой диаграмме, предоставленной Управлением энергетической информации.

Фиксированные уголки наклона солнечных панелей для домов в Калифорнии. Изображение предоставлено EIA.

Заключение: угол наклона солнечной панели имеет значение, но не так много

На производительность солнечных панелей влияет угол их наклона. Чтобы извлечь максимальную мощность из фотоэлектрической системы, вам придется отрегулировать угол в зависимости от широты и времени года.

В реальных ситуациях вам часто приходится иметь дело с фиксированными углами крыши, когда нет возможности отрегулировать или наклонить солнечные системы.

По этой причине солнечные системы устанавливаются под разными углами наклона, чтобы приспособиться к разным наклонам крыш домов, что эффективно экономит деньги домовладельцев.

Итог: Оптимальный угол наклона солнечной панели может увеличить производство, но неспособность достичь его не является решающим фактором.

Узнайте, сколько вы можете сэкономить, перейдя на солнечную батарею

Ключевые выносы

---

• Термин «угол солнечной панели» относится к вертикальному наклону вашей солнечной панели.
• Путь солнца по небу меняется каждый день, что влияет на мощность солнечных батарей.
• Оптимальный угол наклона солнечной панели зависит от географической широты.
• Изменение угла наклона солнечной панели в зависимости от сезона может увеличить выработку электроэнергии, но может значительно увеличить расходы.
• Солнечные панели можно установить на крышах под разными углами — или даже полностью плоско — и при этом сэкономить деньги домовладельцев.

Солнечное излучение на наклонной поверхности

Мощность, падающая на фотоэлектрический модуль, зависит не только от мощности солнечного света, но и от угла между модулем и солнцем. Когда поглощающая поверхность и солнечный свет перпендикулярны друг другу, плотность мощности на поверхности равна плотности мощности солнечного света (другими словами, плотность мощности всегда будет максимальной, когда фотоэлектрический модуль перпендикулярен солнцу) .Однако, поскольку угол между солнцем и неподвижной поверхностью постоянно меняется, плотность мощности на фиксированном фотоэлектрическом модуле меньше, чем у падающего солнечного света.

Количество солнечного излучения, падающего на наклонную поверхность модуля, представляет собой составляющую падающего солнечного излучения, которая перпендикулярна поверхности модуля. На следующем рисунке показано, как рассчитать излучение, падающее на наклонную поверхность (S _модуль ), учитывая либо солнечное излучение, измеренное на горизонтальной поверхности (S _{горизонт} ), либо солнечное излучение, измеренное перпендикулярно солнцу (S _{, падающее} ). .

Наклон модуля к падающему свету снижает мощность модуля.

Уравнения, связывающие модуль S , S _{горизонт} и инцидент S :

$$ S_ {горизонтальный} = S_ {инцидент} \ sin \ alpha $$

$$ S_ {модуль} = S_ {инцидент} \ sin (\ alpha + \ beta) $$

, где
α — угол места; и
β — угол наклона модуля, измеренный от горизонтали.

Угол возвышения ранее задавался как:

.

$$ \ alpha = 90- \ phi + \ delta $$

где \ (\ phi \) — широта; а
\ (\ delta \) — это угол склонения, ранее заданный как

$$ \ delta = 23.{\ circ} \ sin \ left [\ frac {360} {365} (284 + d) \ right] $$

, где d — день года. Обратите внимание, что из простой математики (284 + d) эквивалентно (d-81), которое использовалось ранее. В литературе два уравнения используются как взаимозаменяемые.

Из этих уравнений связь между модулем S и S _{горизонт} может быть определена как:

$$ S_ {module} = \ frac {S_ {Shorizontal} \ sin (\ alpha + \ beta)} {\ sin \ alpha} $$

Следующие активные уравнения показывают расчет падающего и горизонтального солнечного излучения и модуля.Введите только один из S _{, модуль} , S _{горизонт} и S _{инцидент} , и программа вычислит остальные.

Угол наклона существенно влияет на падающее на поверхность солнечное излучение. Для фиксированного угла наклона максимальная мощность в течение года достигается, когда угол наклона равен широте местоположения. Однако более крутые углы наклона оптимизированы для больших зимних нагрузок, в то время как более низкие углы наклона используют большую часть света летом.В приведенном ниже моделировании рассчитывается максимальное количество солнечной инсоляции как функция широты и угла модуля.

Влияние широты и наклона модуля на солнечную радиацию, полученную в течение года в Вт.ч. ^-2 .day ^-1 без облачности. На оси абсцисс день — это количество дней с 1 января. Мощность модуля — это солнечное излучение, падающее на наклоненный модуль. Угол наклона модуля отсчитывается от горизонтали. Падающая мощность — это солнечное излучение, перпендикулярное солнечным лучам, которое будет восприниматься модулем, который идеально отслеживает солнце.Power on Horizontal — это солнечное излучение, падающее на землю, и это то, что может получить модуль, лежащий на земле. Эти значения следует рассматривать как максимально возможные значения в конкретном месте, поскольку они не включают влияние облачного покрова. Предполагается, что модуль обращен на юг в северном полушарии и на север в южном полушарии. Для некоторых углов свет падает с задней части модуля, и в этих случаях мощность модуля падает до 0.

Как видно из приведенной выше анимации, для модуля наклона 0 ° мощность модуля и мощность в горизонтальном положении равны, поскольку модуль лежит на земле.При наклоне модуля 80 ° модуль почти вертикальный. Мощность модуля меньше падающей мощности, за исключением случаев, когда модуль перпендикулярен солнечным лучам и значения равны. Модуль ориентирован на экватор, так что он смотрит на север в Южном полушарии и на юг в Северном полушарии. Когда модуль перемещается из северного в южное полушарие (широта = 0 °), модуль поворачивается лицом в противоположном направлении, и поэтому кривая мощности модуля переворачивается. Когда свет падает с задней стороны модуля, мощность модуля падает до нуля.Попробуйте установить широту своего местоположения, а затем изменить наклон модуля, чтобы увидеть влияние на количество энергии, получаемой в течение года.

Оптимальное расположение и влияние угла наклона на характеристики солнечных фотоэлектрических панелей

1.

Хачича А.А., Аль-Савафта И., Саид З. Влияние пыли на работу солнечных фотоэлектрических систем в погодных условиях Объединенных Арабских Эмиратов. Возобновляемая энергия. 2019; 141: 287–97.

Артикул Google Scholar

2.

Афзал А., Сами АДМ, Разак Р.КА., Рамис М.К., Анализ установившихся и переходных состояний при сопряженной ламинарной принудительной конвекционной теплопередаче. Arch Comput Methods Eng. 2018; 1–36.

3.

Афзал А, Мохаммед Сами А.Д., Абдул Разак РК, Рамис МК. Влияние расстояния на тепловые характеристики литий-ионных аккумуляторных элементов. J Therm Anal Calorim. 2019; 135 (3): 1797–811.

CAS Статья Google Scholar

4.

Грегг А., Паркер Т., Свенсон Р.«Реальное» исследование конструкции и производительности фотоэлектрической системы. В протоколе конференции тридцать первой конференции специалистов по фотовольтаике IEEE; 2005.

5.

Мондол Дж. Д., Йоханис Ю. Г., Нортон Б. Оптимальный размер массива и инвертора для фотоэлектрических систем, подключенных к сети. Sol Energy. 2006. 80 (12): 1517–39.

CAS Статья Google Scholar

6.

Тонуи Дж. К., Трипанагностопулос Ю. Повышение производительности фотоэлектрических солнечных коллекторов с естественным потоком воздуха.Sol Energy. 2008. 82 (1): 1–12.

Артикул Google Scholar

7.

Мусазаде Х., Кейхани А., Джавади А., Мобли Х., Абриния К., Шарифи А. Обзор принципа и методов отслеживания солнца для максимального увеличения производительности солнечных систем. Renew Sustain Energy Rev.2009; 13 (8): 1800–18.

Артикул Google Scholar

8.

Ли С.Й., Чжоу П.С., Чан СМ, Линь С.Ф. Системы слежения за солнцем: обзор.Датчики. 2009; 9: 3875–90.

Артикул PubMed Google Scholar

9.

Мани М., Пиллаи Р. Влияние пыли на работу солнечных фотоэлектрических (ФЭ): состояние исследований, проблемы и рекомендации. Renew Sustain Energy Rev.2010; 14 (9): 3124–31.

Артикул Google Scholar

10.

Чанг Ю.П. Алгоритм гибридной дифференциальной эволюции направления муравьев при определении угла наклона фотоэлектрических модулей.Expert Syst Appl. 2010. 37 (7): 5415–22.

Артикул Google Scholar

11.

Armstrong S, Hurley WG. Тепловая модель фотоэлектрических панелей в различных атмосферных условиях. Appl Therm Eng. 2010. 30 (11–12): 1488–95.

Артикул Google Scholar

12.

Park KE, Kang GH, Kim HI, Yu GJ, Kim JT. Анализ тепловых и электрических характеристик полупрозрачного фотоэлектрического модуля.Энергия. 2010. 35 (6): 2681–7.

CAS Статья Google Scholar

13.

Seme S, Štumberger G. Новый алгоритм прогнозирования солнечных углов с использованием солнечного излучения и дифференциальной эволюции для двухосного отслеживания солнца. Sol Energy. 2011. 85 (11): 2757–70.

Артикул Google Scholar

14.

Ван Ю.Дж., Сюй ПК. Исследование частичного затенения фотоэлектрических модулей с различными конфигурациями подключения фотоэлементов.Энергия. 2011; 36 (5): 3069–78.

Артикул Google Scholar

15.

Берингер С., Шильке Х., Лозе И., Секмайер Г. Пример из практики, показывающий, что угол наклона фотоэлектрических установок почти не имеет значения. Sol Energy. 2011. 85 (3): 470–6.

Артикул Google Scholar

16.

Zogou O, Stapountzis H. Энергетический анализ улучшенной концепции интегрированных фотоэлектрических панелей в офисном здании в центральной Греции.Appl Energy. 2011. 88 (3): 853–66.

Артикул Google Scholar

17.

Хатиб Т., Мохамед А., Сопиан К. Оптимизация фотоэлектрической / ветровой микросети для электрификации сельского жилья с использованием гибридного итеративного / генетического алгоритма: тематическое исследование Куала-Теренггану, Малайзия. Энергетика. 2012; 47: 321–31.

Артикул Google Scholar

18.

Хаммон М., Денхольм П., Марголис Р.Влияние фотоэлектрической ориентации на ее относительную экономическую ценность на оптовых рынках энергии; 2012.

19.

Khare A, Rangnekar S. Обзор оптимизации роя частиц и ее применения в солнечных фотоэлектрических системах. Appl Soft Comput J. 2013; 13 (5): 2997–3006.

Артикул Google Scholar

20.

Эндрюс Р.В., Пирс Дж. М.. Влияние спектрального альбедо на работу солнечных фотоэлектрических устройств из аморфного кремния и кристаллического кремния.Sol Energy. 2013; 91: 233–41.

CAS Статья Google Scholar

21.

Ядав А.К., Чандель С.С. Оптимизация угла наклона для максимального увеличения падающего солнечного излучения: обзор. Renew Sustain Energy Rev.2013; 23: 503–13.

Артикул Google Scholar

22.

Кумар М., Афзал А, Рамис МК. Исследование физико-химических и трибологических свойств наносмазочного масла TiO2 различной концентрации.Трибол финский J Трибол. 2017; 35 (3): 6–15.

Google Scholar

23.

Афзал А., Мохаммед Сами А.Д., Абдул Дж., Ахамед Шафван С., Аджинас П.В., Ахаммедул Кабир К.М. Анализ теплопередачи гладких трубок и труб с ямочками с разным расстоянием между ними ». Теплопередача. Res. 2018; 47 (3): 556–68.

Артикул Google Scholar

24.

Афзал А, Сами АДМ, Разак РКА. Сравнительный анализ тепловых характеристик воды, охлаждающей жидкости двигателя и наножидкости MWCNT-W в радиаторе.Модель Meas Control B. 2018; 87 (1): 1–6.

Артикул Google Scholar

25.

Афзал А, Сами АДМ, Разак РКА, Рамис МК. Характеристики теплопередачи наножидкости MWCNT в прямоугольных мини-каналах. Int J Heat Technol. 2018; 36 (1): 222–8.

Артикул Google Scholar

26.

Афзал А, Мохаммед Сами А.Д., Абдул Разак РК. Экспериментальное термическое исследование наножидкости CuO – W в круговом миниканале.Модель Meas Control B. 2017; 86 (2): 335–44.

Артикул Google Scholar

27.

Каплани Э., Капланис С. Тепловое моделирование и экспериментальная оценка зависимости температуры фотоэлектрического модуля от скорости и направления ветра, ориентации и наклона модуля. Sol Energy. 2014; 107: 443–60.

Артикул Google Scholar

28.

Bianchi C, Smith AD. Влияние освещенности и температуры окружающей среды на инструмент для принятия решений по выбору размеров фотоэлектрических панелей на крышах коммерческих зданий.В: 10-я международная конференция ASME 2016 по устойчивому развитию энергетики, совмещенная с энергетической конференцией ASME 2016 и 14-й международной конференцией ASME 2016 по науке, технике и технологиям топливных элементов. Американское общество инженеров-механиков; 2016.

29.

Hsu PC, et al. Влияние схемы переключения на производительность гибридной солнечной фотоэлектрической системы. Возобновляемая энергия. 2016; 96: 520–30.

Артикул Google Scholar

30.

Wu Y, Wu S, Xiao L. Характеристики рассеивания тепла от фотоэлектрических элементов в разделенной или неразделенной застекленной полости в ветреную среду. Возобновляемая энергия. 2018; 127: 642–52.

Артикул Google Scholar

31.

Zsiborács H, et al. Изменение реального и смоделированного производства энергии некоторыми фотоэлектрическими технологиями в зависимости от ориентации, угла наклона и двухосного слежения за солнцем. Пример из Венгрии.Поддерживать. 2018; 10 (5): 1–19.

Артикул Google Scholar

32.

Notton G, Muselli M, Louche A. Два метода оценки среднемесячного часового суммарного облучения наклонных поверхностей на основе среднемесячного дневного горизонтального облучения на основе данных солнечной радиации в Аяччо, Корсика. Sol Energy. 1996; 57 (2): 141–53.

Артикул Google Scholar

33.

Soulayman SS. Об оптимальном наклоне пластин солнечного поглотителя.Возобновляемая энергия. 1991; 1 (3): 551–4.

CAS Статья Google Scholar

34.

Krauter S. Повышенный выход электроэнергии за счет потока воды через переднюю часть фотоэлектрических панелей. Sol Energy Mater Sol Cells. 2004. 82 (1–2): 131–7.

CAS Статья Google Scholar

35.

Ройн А., Дей С.Дж. Конструкция устройства струйного охлаждения для плотно упакованных фотоэлементов при высокой концентрации.Sol Energy. 2007. 81 (8): 1014–24.

CAS Статья Google Scholar

36.

Solanki CS, Sangani CS, Gunashekar D, Antony G. Улучшенное рассеивание тепла фотоэлектрических модулей с V-образным желобом для повышения производительности. Sol Energy Mater Sol Cells. 2008. 92 (12): 1634–8.

CAS Статья Google Scholar

37.

Ван И, Фанг З., Чжу Л., Хуанг К., Чжан Ю., Чжан З. Характеристики кремниевых солнечных элементов, работающих в жидкостях.Appl Energy. 2009. 86 (7–8): 1037–42.

CAS Статья Google Scholar

38.

Maiti S, Vyas K, Ghosh PK. Работоспособность кремниевого фотоэлектрического модуля при усиленном освещении и селективной фильтрации падающего излучения с одновременным охлаждением. Sol Energy. 2010. 84 (8): 1439–44.

CAS Статья Google Scholar

39.

Malvi CS, Dixon-Hardy DW, Crook R.Модель баланса энергии комбинированной фотоэлектрической солнечно-тепловой системы, включающей материал с фазовым переходом. Sol Energy. 2011. 85 (7): 1440–6.

CAS Статья Google Scholar

40.

Ким Дж. П., Лим Х, Сон Дж. Х., Чанг Й. Дж., Чон Ч. Численный анализ тепловых характеристик фотоэлектрического модуля при изменении температуры окружающей среды. Sol Energy Mater Sol Cells. 2011; 95 (1): 404–7.

CAS Статья Google Scholar

41.

Лю Л., Чжу Л., Ван И, Хуанг Ц., Сунь Ю., Инь З. Характеристики рассеивания тепла кремниевых солнечных элементов за счет прямого погружения в диэлектрическую жидкость при интенсивном освещении. Sol Energy. 2011; 85 (5): 922–30.

CAS Статья Google Scholar

42.

Керцманн Т., Шефер Л. Системное моделирование линейной концентрирующей фотоэлектрической системы с активной системой охлаждения. Возобновляемая энергия. 2012; 41: 254–61.

Артикул Google Scholar

43.

Teo HG, Lee PS, Hawlader MNA. Активная система охлаждения для фотоэлектрических модулей. Appl Energy. 2012; 90 (1): 309–15.

Артикул Google Scholar

44.

Tina GM, Rosa-Clot M, Rosa-Clot P, Scandura PF. Оптические и тепловые характеристики погруженной фотоэлектрической солнечной панели: SP2. Энергия. 2012. 39 (1): 17–26.

CAS Статья Google Scholar

45.

Rustemli S, Dincer F, Unal E, Karaaslan M, Sabah C.Анализ систем слежения за солнцем и охлаждения для фотоэлектрических панелей. Renew Sustain Energy Ред. 2013; 22: 598–603.

Артикул Google Scholar

46.

Кахул Н., Уабес М., Садок М. Оценка раннего ухудшения характеристик фотоэлектрических модулей в регионе Сахары. Energy Convers Manag. 2014; 82: 320–6.

Артикул Google Scholar

47.

Карами Н., Рахими М.Повышение теплопередачи в гибридном микроканальном фотоэлектрическом элементе с использованием наножидкости Boehmite. Int Коммунальный тепломассообмен. 2014; 55: 45–52.

CAS Статья Google Scholar

48.

Nižetić S, Arıcı M, Bilgin F, Grubišić-Čabo F. Исследование свиного жира как потенциально нового материала с фазовым переходом для пассивного охлаждения в фотовольтаике. J Clean Prod. 2018; 170: 1006–16.

Артикул Google Scholar

49.

Arıcı M, Bilgin F, Nižetić S, Papadopoulos AM. Охлаждение фотоэлектрической панели на основе материала с фазовым переходом: упрощенная численная модель для оптимизации слоя материала с фазовым переходом и общей экономической оценки. J Clean Prod. 2018; 189: 738–45.

Артикул Google Scholar

50.

Пепелышев А., Стеланд А., Авеллан-Хампе А. Планы приемочного контроля фотоэлектрических модулей с двусторонними пределами спецификации.Prog Photovolt Res Appl. 2014. 22 (6): 603–11.

Артикул Google Scholar

51.

Карами Н., Рахими М. Улучшение теплопередачи в фотоэлектрической ячейке с использованием наножидкости Boehmite. Energy Convers Manag. 2014; 86: 275–85.

CAS Статья Google Scholar

52.

Wu S, Xiong C. Технология пассивного охлаждения фотоэлектрических панелей для жилых домов. Int J Low-Carbon Technol.2014. 9 (2): 118–26.

Артикул Google Scholar

53.

Irwan YM, et al. Проведение испытаний фотоэлектрической панели методом водяного охлаждения в помещении, об. 79. Хобокен: Эльзевир; 2015.

Google Scholar

54.

Рахман М.М., Хасануззаман М., Рахим Н.А. Влияние различных параметров на мощность и КПД фотоэлектрического модуля. Energy Convers Manag. 2015; 103: 348–58.

Артикул Google Scholar

55.

Sahay A, Sethi VK, Tiwari AC, Pandey M. Обзор солнечных фотоэлектрических панельных систем охлаждения с особым акцентом на наземную систему охлаждения центральной панели (GC-CPCS). Renew Sustain Energy Rev.2015; 42: 306–12.

Артикул Google Scholar

56.

Хасануззаман М., Малек АБМА, Ислам М.М., Пандей А.К., Рахим Н.А. Глобальное развитие технологий охлаждения для фотоэлектрических систем: обзор. Sol Energy. 2016; 137: 25–45.

Артикул Google Scholar

57.

Лю Б., Джордан Р. Ежедневная инсоляция поверхностей, наклоненных к экватору. ASHRAE J. 1961; 10.

58.

Цалидес П., Танаилакис А. Прямое вычисление оптимального угла наклона массива в фотоэлектрических системах с постоянным наклоном. Sol Cells. 1985. 14 (1): 83–94.

Артикул Google Scholar

59.

Якуп МАХМ, Малик AQ. А.К. Малик (2001) Оптимальный угол наклона и ориентация солнечного коллектора в Брунее-Даруссаламе. Обновить.Энергия. 2001. 24 (9): 223–34.

CAS Статья Google Scholar

60.

Ульген К. Оптимальный угол наклона для солнечных коллекторов. Источники энергии Часть A Восстановление Util Environ Effic. 2006. 28 (13): 1171–80.

CAS Статья Google Scholar

61.

Гунерхан Х., Хепбасли А. Определение оптимального угла наклона солнечных коллекторов для строительства. Сборка Environ.2007. 42 (2): 779–83.

Артикул Google Scholar

62.

Чанг ТП. Исследование оптимального угла наклона солнечного коллектора в зависимости от различных типов излучения. Int J Appl Sci Eng. 2008. 6 (2): 151–61.

Google Scholar

63.

Чжао К., Ван П., Гоэль Л. Оптимальный угол наклона фотоэлектрической панели на основе прогноза солнечной радиации. В: 2010 г. 11-я Международная конференция IEEE по вероятностным методам, применяемым к энергетическим системам (PMAPS 2010), 2010 г .; С. 425–430.

64.

Tang R, Gao W, Yu Y, Chen H. Оптимальные углы наклона полностью стеклянных вакуумных солнечных коллекторов. Энергия. 2009. 34 (9): 1387–95.

Артикул Google Scholar

65.

Даут И., Ирванто М., Ирван Ю.М., Гомеш Н., Ахмад Н.С. Глобальное солнечное излучение в ясном небе по углам наклона фотоэлектрического модуля в Перлисе, Северная Малайзия. В: INECCE 2011: 1-я международная конференция по электротехнике, контролю и вычислительной технике, 2011 г .; С. 445–450.

66.

Pour HSS, Beheshti HK, Rahnama M. Прирост энергии под оптимальными углами солнечных панелей в течение года в Исфахане, Иран. Источники энергии Часть A Восстановление Util Environ Effic. 2011; 33 (13): 1281–90.

Артикул Google Scholar

67.

Elhab BR, et al. Оптимизация углов наклона и ориентации солнечных панелей для Куала-Лумпур, Малайзия. Sci Res Essays. 2012. 7 (42): 3758–67.

Google Scholar

68.

Сандеран П., Исмаил А., Сингх Б. Оптимальный угол наклона и ориентация автономных фотоэлектрических систем производства электроэнергии для электрификации сельских районов. J Appl Sci. 2011; 11 (7): 1219–24.

Артикул Google Scholar

69.

Т. Хатиб, А. Мохамед и К. Сопиан, «Об оптимальном месячном угле наклона солнечной панели для пяти объектов в Малайзии. В: 2012 Международная конференция по энергетике и оптимизации IEEE (PEOCO) 2012 — Материалы конференции., нет. Июнь 2012 г .; С. 7–10.

70.

Agarwal A, Vashishtha VK, Mishra SN. Сравнительный подход к оптимизации угла наклона для получения максимального излучения. Int J Eng Res Technol. 2012; 1 (5): 1–9.

Google Scholar

71.

Sun L, Lu L, Yang H. Оптимальный дизайн фотоэлектрических облицовок, интегрированных в здание, с различными углами азимута поверхности. Appl Energy. 2012; 90 (1): 233–40.

Артикул Google Scholar

72.

Хорасанизаде Х., Мохаммади К., Мостафаейпур А. Создание модели рассеянного солнечного излучения для определения оптимального угла наклона солнечных поверхностей в Табассе, Иран. Energy Convers Manag. 2014; 78: 805–14.

Артикул Google Scholar

73.

Друри Э., Лопес А., Денхольм П., Марголис Р. Относительные характеристики отслеживания по сравнению с фотоэлектрическими системами с фиксированным наклоном в США. Prog Photovoltaics Res Appl. 2014; 22: 1302–15.

Google Scholar

74.

Khoo YS, Reindl T, Aberle AG, Member S. Оптимальная ориентация и угол наклона для максимального увеличения солнечного излучения в плоскости для фотоэлектрических систем в Сингапуре. IEEE J Photovolt. 2014. 4 (2): 647–53.

Артикул Google Scholar

75.

Hartner M, Ortner A, Hiesl A, Haas R. С востока на запад — оптимальный угол наклона и ориентация фотоэлектрических панелей с точки зрения энергосистемы. Appl Energy. 2015; 160: 94–107.

Артикул Google Scholar

76.

Деспотович М., Недич В. Сравнение оптимальных углов наклона солнечных коллекторов, определенных на годовом, сезонном и месячном уровнях. Energy Convers Manag. 2015; 97: 121–31.

Артикул Google Scholar

77.

Фархан С., Таббассум К., Талпур С., Букс М. Оценка ресурсов солнечной энергии путем создания эмпирических моделей рассеянного солнечного излучения на наклонной поверхности и анализа оптимального угла наклона для перспективного местоположения в южном регионе Синда, Пакистан.Int J Electr Power Energy Syst. 2015; 64: 1073–80.

Артикул Google Scholar

78.

Сулейман С., Саббаг В. Оптимальный наклон и ориентация солнечного коллектора. Откройте J Renew Sustain Energy. 2015; 2 (1): 1–9.

Артикул Google Scholar

79.

Нижегородов Н., Деван К.РС, Джейн П.К., Карлссон С. Модели пропускания атмосферы и пластины поглотителя, ориентированные по-разному на любой широте.Возобновляемая энергия. 1994. 4 (5): 529–43.

Артикул Google Scholar

80.

Calabrò E. Алгоритм определения оптимального угла наклона. J Renew Energy. 2013; 2013: 12.

Google Scholar

81.

Ахлаги С., Сангроди Х., Сарайлоо М., Резаиахари М. Эффективная работа бытовых солнечных панелей с определением оптимального угла наклона и оптимальных интервалов на основе модели прогнозирования.IET Renew Power Gener. 2017; 11: 1261–7.

Артикул Google Scholar

82.

Трипати М., Ядав С., Садху П.К., Панда С.К. Определение оптимального угла наклона и точной инсоляции панели BIPV под влиянием неблагоприятного влияния тени. Возобновляемая энергия. 2017; 104: 211–23.

Артикул Google Scholar

83.

Ядав С., Панда С.К., Трипати М. Характеристики построения интегрированной фотоэлектрической тепловой системы с фотоэлектрическим модулем, установленным под оптимальным углом наклона и подверженным влиянию тени.Возобновляемая энергия. 2018; 127: 11–23.

Артикул Google Scholar

84.

Conceição R, Silva HG, Fialho L, Lopes FM, Collares-Pereira M. Конструкция фотоэлектрической системы с эффектом загрязнения для оптимального угла наклона. Возобновляемая энергия. 2019; 133: 787–96.

Артикул Google Scholar

85.

Shariah A, Al-Akhras MA, Al-Omari IA. Оптимизация угла наклона солнечных коллекторов. Возобновляемая энергия.2002; 26: 587–98.

Артикул Google Scholar

86.

Hussein HMS, Ahmad GE, El-Ghetany HH. Оценка производительности фотоэлектрических модулей при различных углах наклона и ориентации. Energy Convers Manag. 2004. 45 (15–16): 2441–52.

CAS Статья Google Scholar

87.

Calabrò E. Определение оптимальных углов наклона фотоэлектрических панелей в типичных северных тропических широтах.J Renew Sustain Energy. 2009; 1 (3): 033104.

Артикул Google Scholar

88.

Бенганем М. Оптимизация угла наклона солнечной панели: тематическое исследование для Медины, Саудовская Аравия. Appl Energy. 2011. 88 (4): 1427–33.

Артикул Google Scholar

89.

Ахмад М.Дж., Тивари, штат Джорджия. Оптимизация угла наклона солнечного коллектора для получения максимального излучения. Открытая возобновляемая энергия J.2009; 2: 19–24.

Артикул Google Scholar

90.

Роулендс И.Х., Кемери Б.П., Босолей-Моррисон И. Оптимальный угол наклона и азимут солнечной фотоэлектрической системы: тематическое исследование Онтарио (Канада). Энергетическая политика. 2011. 39 (3): 1397–409.

Артикул Google Scholar

91.

Бодич М., Бигот Д., Миранвиль Ф., Парведи-Пату А., Радулович Я. Оптимизация характеристик фотоэлектрических систем на острове Реюньон — угол наклона.Prog Photovolt Res Appl. 2011. 20 (8): 923–35.

Артикул CAS Google Scholar

92.

Эмам М., Оокавара С., Ахмед М. Исследование характеристик и анализ наклонной концентрированной системы материалов с фотоэлектрическим фазовым переходом. Sol Energy. 2017; 150: 229–45.

Артикул Google Scholar

93.

Родс Дж. Д., Апшоу К. Р., Коул В. Дж., Холкомб К. Л., Уэббер М. Е.. Многоцелевая оценка влияния ориентации и наклона солнечных панелей на производство энергии и экономику системы.Sol Energy. 2014; 108: 28–40.

Артикул Google Scholar

94.

Gharakhani Siraki A, Pillay P. Исследование оптимальных углов наклона солнечных панелей в различных широтах для городских приложений. Sol Energy. 2012. 86 (6): 1920–8.

Артикул Google Scholar

95.

Даффи Дж., Бекман В. Солнечная инженерия тепловых процессов. 3-е изд. Нью-Йорк: Уайли; 1980.

Google Scholar

96.

Варгас О., Пинилла Г., Васкес Дж. Определение размеров и изучение производства энергии в фотоэлектрической системе, привязанной к сети, с использованием программного обеспечения PV syst. TECCIENCIA. 2017; 12 (22): 27–32.

Google Scholar

97.

Кханна С., Редди К.С., Маллик Т.К. Анализ производительности наклонной фотоэлектрической системы, интегрированной с материалом с фазовым переходом, в различных рабочих условиях. Энергия. 2017; 133: 887–99.

Артикул Google Scholar

98.

Лу Х., Чжао В. Влияние размеров частиц и углов наклона на характеристики осаждения пыли наземной солнечной фотоэлектрической системы. Appl Energy. 2018; 220 (2018): 514–26.

Артикул Google Scholar

99.

Лау К.Й., Тан CW, Ятим АХМ. Влияние температуры окружающей среды, углов наклона и ориентации на гибридные фотоэлектрические / дизельные системы в условиях экваториального климата. Renew Sustain Energy Rev.2018; 81 (июнь): 2625–36.

Артикул Google Scholar

100.

Али Морад А.М., Аль-Сайяб АКС, Абдулвахид М.А. Оптимизация углов наклона фотоэлектрического элемента для определения максимальной генерируемой электроэнергии: на примере некоторых иракских городов. Case Stud Therm Eng. 2018; 12: 484–8.

Артикул Google Scholar

101.

Якобсон М.З., Джадхав В. Мировые оценки оптимальных углов наклона и отношения солнечного света, падающего на наклонные и отслеживаемые фотоэлектрические панели, относительно горизонтальных панелей. Sol Energy.2017; 169: 55–66.

Артикул Google Scholar

102.

Кумар Н.М., Динния ФС. Влияние угла наклона на выработку энергии и коэффициенты производительности фотоэлектрических генераторов, подключенных к сети в Юго-Восточной Азии. Prog Ind Ecol Int J. 2019; 13 (3): 264.

Артикул Google Scholar

103.

Аль Гарни Х.З., Авасти А., Райт Д. Оптимальные углы ориентации для максимизации выхода энергии для солнечных фотоэлектрических систем в Саудовской Аравии.Возобновляемая энергия. 2019; 133: 538–50.

Артикул Google Scholar

104.

Асл-Сулеймани Э, Фарханги С., Забихи МС. Влияние угла наклона и загрязнения воздуха на работу фотоэлектрических систем в Тегеране. Возобновляемая энергия. 2001. 24 (3–4): 459–68.

CAS Статья Google Scholar

105.

Kacira M, Simsek M, Babur Y, Demirkol S. Определение оптимальных углов наклона и ориентации фотоэлектрических панелей в Шанлыурфе, Турция.Возобновляемая энергия. 2004. 29 (8): 1265–75.

Артикул Google Scholar

106.

Эльхассан ЗАМ, Заин MFM, Сопиан К., Авадалла А. Выходная энергия фотоэлектрического модуля, направленная под оптимальным углом наклона, в Куала-Лумпуре, Малайзия. Res J Appl Sci. 2011; 6 (2): 104–9.

Артикул Google Scholar

107.

Xu R, Ni K, Hu Y, Si J, Wen H, Yu D. Анализ оптимального угла наклона для загрязненной фотоэлектрической панели.Energy Convers Manag. 2017; 148: 100–9.

Артикул Google Scholar

108.

Fahl P, Ganapathisubbu SG. Отслеживание выгод для солнечных коллекторов, установленных в Бангалоре. J Renew Sustain Energy. 2011; 3 (2): 1–12.

Артикул Google Scholar

109.

Sun LL, Li M, Yuan YP, Cao XL, Lei B, Yu NY. Влияние угла наклона и режима подключения PVT-модулей на энергоэффективность системы горячего водоснабжения многоэтажных жилых домов.Возобновляемая энергия. 2016; 93: 291–301.

Артикул Google Scholar

110.

Абдин Э., Ораби М., Хасанин Э. Оптимальный угол наклона фотоэлектрической системы в условиях пустыни. Sol Energy. 2017; 155: 267–80.

Артикул Google Scholar

111.

Чжи Чжан Л., Цзян Пан А., Ронг Кай Р., Лу Х. Эксперименты по уменьшению осаждения пыли на стекле солнечных элементов с помощью прозрачного супергидрофобного покрытия с разными углами наклона.Sol Energy. 2019; 188: 1146–55.

Артикул CAS Google Scholar

112.

Asowata O, Swart J, Pienaar C. Оптимальные углы наклона фотоэлектрических панелей в зимние месяцы в треугольнике ваал, Южная Африка. Smart Grid Renew. Энергия. 2012; 03 (02): 119–25.

Артикул Google Scholar

113.

Лю Х. Расчет и анализ оптимального угла наклона для гибридного коллектора PV / T.В: Материалы международной конференции 2012 г. по интеллектуальному проектированию и применению систем (ISDEA) 2012 г .; С. 791–795.

114.

Калделлис Дж., Зафиракис Д. Экспериментальное исследование оптимального угла наклона фотоэлектрических панелей в летний период. Энергия. 2012. 38 (1): 305–14.

Артикул Google Scholar

115.

Eldin SAS, Abd-elhady MS, Kandil HA. Возможность использования солнечных систем слежения для фотоэлектрических панелей в горячих и холодных регионах.Возобновляемая энергия. 2016; 85: 228–33.

Артикул Google Scholar

116.

Каддура ТО, Рамли МАМ, Аль-Турки Я.А. Об оценке оптимального угла наклона фотоэлектрической панели в Саудовской Аравии. Renew Sustain Energy Ред. 2016; 65: 626–34.

Артикул Google Scholar

117.

Malek NAAA, Chew JM, Naamandadin NA. Исследование связи между углом наклона, воздействием солнечной инсоляции и мощностью солнечной фотоэлектрической панели с использованием 3D-моделирования BIM.В: Сеть конференций MATEC (ICRMCE 2018), 2018; т. 195, 06009, стр. 11.

118.

Уллах А., Имран Х., Максуд З., Батт, Новая Зеландия. Исследование оптимальных углов наклона и влияния загрязнения на производство фотоэлектрической энергии в Пакистане. Возобновляемая энергия. 2019; 139: 830–43.

Артикул Google Scholar

Алгоритм для определения оптимального угла наклона солнечной панели на основе глобального горизонтального солнечного излучения

В этой статье предлагается алгоритм для расчета оптимального угла наклона солнечных панелей с помощью данных глобального горизонтального солнечного излучения, полученных с Земли. метеостанции.Это математическое моделирование основано на максимизации теоретического выражения глобального солнечного излучения, падающего на наклонную поверхность, относительно наклона и ориентации панели и солнечного часового угла. В результате получился ряд превосходных уравнений, решения которых дают оптимальный наклон и ориентацию солнечной панели. Моделирование проводилось с использованием данных глобального горизонтального солнечного излучения из Европейского атласа солнечной радиации и некоторых эмпирических моделей диффузного солнечного излучения.Полученный оптимальный угол наклона был связан с широтой линейной регрессией со значительными коэффициентами корреляции. Стандартная ошибка средних значений значительно увеличивалась с увеличением широты, что позволяет предположить, что ненадежные значения могут быть получены в высоких широтах.

1. Введение

Большинство стран мира осознали необходимость сокращения выбросов газов, чтобы противостоять неблагоприятным глобальным климатическим изменениям, поощряя использование возобновляемых и устойчивых источников энергии.Действительно, большие количества углекислого газа, азота и оксидов серы выбрасываются в мир обычными источниками энергии, которые выбрасываются в атмосферу Земли, способствуя изменению климата.

Кроме того, в мире скоро закончатся традиционные энергетические ресурсы из-за быстрого истощения запасов ископаемого топлива. Этот сценарий будущего и риски, связанные с выбросами CO ₂ и глобальным потеплением, повысили интерес к возобновляемым источникам энергии.

Основные системы возобновляемых источников энергии включают фотоэлектрические (PV), солнечные тепловые, ветровые, биомассовые, гидроэлектрические и геотермальные.Однако среди различных возобновляемых источников энергии фотоэлектрическая технология для выработки электроэнергии считается хорошо подходящей технологией, особенно для распределенной выработки электроэнергии.

Солнечные панели являются основным компонентом преобразования энергии фотоэлектрических систем или солнечных коллекторов. Солнечные панели используют световую энергию солнца для выработки электроэнергии за счет фотоэлектрического эффекта, тогда как солнечные тепловые системы вырабатывают тепло.

Количество электроэнергии, производимой фотоэлектрическими системами, связано с количеством солнечного излучения, проецируемого на модули.Следовательно, для оценки тепловой и электрической мощности, получаемой при архитектурном планировании, следует учитывать глобальное солнечное излучение на наклонных поверхностях, обращенных в разные стороны.

В литературе указано, что солнечная энергия, подаваемая модулями, зависит от многих внешних факторов, таких как уровень солнечного излучения, температура, условия нагрузки и ориентация панели.

Солнечная радиация также зависит от характера и степени облачности и содержания водяного пара в атмосфере, поскольку солнечная радиация, попадающая в атмосферу Земли, рассеивается атмосферными газами, аэрозолями и облаками.

Действительно, метеорологические параметры, используемые в качестве предикторов, включают количество и распределение облаков или другие наблюдения, такие как относительное количество солнечного света и содержание воды [1, 2].

Аэрозоли могут поглощать или рассеивать излучение и изменять энергетический баланс Земли, особенно при ясном небе [3].

Эти параметры, очевидно, не могут быть изменены, в то время как другие переменные могут быть изменены, чтобы максимизировать солнечную энергию, получаемую панелью. Фактически, конструкция модуля солнечной энергии включает в себя сложные компромиссы из-за взаимодействия нескольких факторов, таких как характеристики солнечных элементов, требования к источнику питания и особенности управления питанием встроенной системы, поведение приложения, наклон и ориентация панель.

Следовательно, важно понимать и использовать эти факторы, чтобы максимизировать энергоэффективность солнечного модуля.

В частности, для неподвижных поверхностей поглотителя получение солнечной энергии строго связано с наклоном и азимутальным углом солнечной панели.

Глобальное солнечное излучение для наклонных поверхностей может быть рассчитано по значениям прямого и рассеянного солнечного излучения на соответствующей горизонтальной поверхности. Чтобы узнать горизонтальную глобальную солнечную радиацию, необходимы метеорологические данные из всех частей мира, а для некоторых регионов данные измерений могут применяться только в радиусе примерно 50 км от метеостанций.Это обстоятельство приводит к интерполяции параметров между станциями.

Кроме того, спектральная энергетическая освещенность обычно не измеряется рутинно, поэтому мгновенное производство энергии солнечной установкой должно основываться на соответствующих моделях.

В противном случае пользователям необходимы точные вычисления наклона и ориентации солнечных панелей, чтобы максимизировать солнечную энергию, собираемую фиксированными солнечными панелями.

Преимущества стационарных солнечных панелей в основном связаны с их устойчивостью к смещению, так как примерно 20% падающего солнечного излучения представляет собой рассеянный свет, доступный под любым углом смещения по отношению к прямому солнцу.

Напротив, основным преимуществом систем слежения является сбор солнечной энергии в течение самого длительного периода дня с наиболее точным выравниванием, поскольку положение солнца меняется в зависимости от времени года. Действительно, дневная солнечная энергия, собираемая солнечной панелью с одной осевой системой слежения «восток-запад», была на 19–24% выше, чем стационарной системой [4].

Тем не менее, поскольку солнечные системы слежения требуют высоких затрат на эксплуатацию и техническое обслуживание и не всегда применимы, часто бывает удобно установить солнечный коллектор на фиксированное значение оптимального угла наклона [5].

Однако недавно были предложены некоторые алгоритмы минимизации потерь энергии, генерируемых приводным исполнительным механизмом [6, 7].

В противном случае увеличение рассеянной солнечной радиации на низких широтах в некоторых местах по сравнению с высокими широтами делает фиксированные солнечные панели конкурентоспособной альтернативой другим источникам энергии, главным образом в этих местах [8].

Таким образом, возникает следующий главный вопрос относительно конструкции стационарных солнечных панелей.

Какой наклон и ориентацию солнечной панели нужно выбрать, чтобы максимизировать солнечное излучение?

Солнечное излучение, падающее на наклонную поверхность, можно разделить на прямое, диффузное и отраженное от земли.Следовательно, чтобы ответить на этот фундаментальный вопрос, необходимо изучить метод определения этих величин для каждой широты.

Рассеянная солнечная составляющая — это самая сложная величина для определения, потому что распределение рассеянной по небу яркости строго зависит от местных условий неба.

Одним из способов оценки рассеянной солнечной составляющей является изучение регрессии между глобальным и рассеянным солнечным излучением в местах, где имеются соответствующие данные, создание моделей, которые можно использовать для прогнозирования рассеянного солнечного излучения.

Лю и Джордан выполнили первые исследования по этому вопросу, определив взаимосвязь между дневной диффузной и глобальной радиацией на горизонтальной поверхности, предполагая изотропное распространение солнечного излучения в небе [9].

Erbs et al. использовал базу данных, полученную с четырех метеостанций США, состоящую из часового прямого нормального излучения и глобального излучения, для разработки оценки диффузной доли среднечасового, дневного и месячного среднего глобального излучения [10].

Кроме того, [11, 12] использовали также два предиктора для их корреляций: индекс ясности и высоту Солнца.

Гаррисон предложил модель для представления зависимости диффузной фракции от альбедо поверхности, атмосферных осадков, мутности атмосферы, высоты Солнца и глобального горизонтального излучения [13].

Reindl et al. рассмотрены еще два важных предиктора, температура окружающей среды и относительная влажность [14], уменьшающие стандартную ошибку моделей типа Лю и Джордана.

С другой стороны, [15] разработал экспоненциальную модель для оценки излучения прямого нормального пучка от глобального излучения, названную моделью диска.Затем эта модель была улучшена в [16].

Однако точное математическое моделирование глобального и рассеянного солнечного излучения, которое использовалось для моделирования в этом исследовании, предлагается в следующем разделе.

В литературе приводятся различные оптимальные значения угла наклона для фиксированных солнечных панелей.

Например, Цю и Риффат предложили установить угол наклона солнечного коллектора в пределах оптимального угла наклона ± 10 ° как приемлемую практику [17].

Прочие вычисления привели к значениям [18], [19], [20] и [21], где обозначает географическую широту, а знаки + и — относятся к зимним и летним месяцам соответственно.

Расхождение между этими значениями может быть вызвано двумя основными причинами: (1) во-первых, разными методами расчета, которые использовались для определения оптимального значения наклона солнечной панели; (2) во-вторых, разными эмпирическими моделями которые учитывались для определения рассеянной солнечной яркости и ее связи с количеством глобальной солнечной радиации.

Целью этого исследования было предложить алгоритм для определения оптимального наклона и ориентации солнечной панели с использованием математической модели, основанной на ориентации общей поверхности по отношению к положению солнца на небе.Другие физические переменные и эмпирическая модель рассеянного солнечного излучения последовательно рассматриваются в алгоритме, связывая его с конкретным местоположением.

2. Математическое моделирование глобального и диффузного солнечного излучения

В литературе представлено несколько методов оценки глобального и рассеянного солнечного излучения с использованием климатологических параметров.

Типичной эмпирической моделью является уравнение регрессии типа Ангстрема [22] где — среднемесячная дневная глобальная солнечная радиация, падающая на горизонтальную поверхность в определенном месте, — это среднемесячная дневная радиация на горизонтальной поверхности в отсутствие атмосферы, — это среднемесячное значение суточного числа часов наблюдаемого солнечного сияния, — среднемесячное значение продолжительности светового дня в интересующем населенном пункте, а «» и «» — константы регрессии, определенные по климатологическим данным.Это соотношение часто называют «процентом возможного солнечного сияния».

Коэффициенты регрессии «» и «» могут быть получены из некоторых соотношений, предложенных в [23, 24].

Статистически во всем мире среднее снижение глобальной солнечной радиации на 5,3%, с наибольшим снижением между 45 ° и 30 ° с.ш., было обнаружено путем анализа данных, собранных на 45 актинометрических станциях в 1958, 1965, 1975 и 1985 годах [25] . Значительное уменьшение среднегодовой глобальной солнечной радиации между 1964 и 1990 годами при полной облачности было обнаружено в некоторых местах Германии [26].

Наблюдаемые изменения в радиации при ясном небе могут быть связаны с восстановлением вследствие извержения вулканов частиц субмикронного аэрозоля с одновременным уменьшением массовой концентрации аэрозоля и увеличением поглощения городским аэрозолем.

Следовательно, данные о глобальном горизонтальном солнечном облучении следует обновлять и отдавать предпочтение эмпирическим выражениям, таким как (1).

В противном случае суточное внеземное излучение на горизонтальной поверхности, названное, может быть вычислено для дня по следующему уравнению [27]: где — солнечная постоянная (1367 Вт / м ² ), — номер дня, — склонение Солнца и — географическая широта.Часовой угол восхода солнца был выражен как функция уравнения Купера.

Отношение солнечной радиации на поверхности Земли к внеземной радиации называется индексом ясности со средним месячным индексом ясности, определяемым как где — среднемесячная дневная солнечная радиация на горизонтальной поверхности.

Глобальное горизонтальное солнечное облучение, обеспечиваемое метеорологическими станциями, включает горизонтальное облучение прямым пучком и горизонтальное рассеянное облучение неба.

Некоторые модели могут преобразовывать глобальное горизонтальное облучение в прямое лучевое облучение и диффузное облучение неба в горизонтальной плоскости с помощью эмпирических соотношений.

Heliosat — это алгоритм, который был разработан для оценки глобальной горизонтальной освещенности на уровне земли с использованием изображений спутников Meteosat, сделанных в видимом диапазоне.

Некоторые прогностические модели для оценки глобального солнечного излучения должны использоваться для получения солнечного излучения на наклонной поверхности, чтобы можно было оценить взаимосвязь между глобальным солнечным излучением на горизонтальных плоскостях и на наклонных плоскостях [9, 28–31 ].

К сожалению, никакая теоретическая взаимосвязь между горизонтальным рассеянным излучением неба и горизонтальным глобальным солнечным излучением не может быть точно определена. Действительно, необходимо решить двойной интеграл, подобный уравнению (5) из [32], который не может быть вычислен даже в простейшем случае однородного и изотропного рассеянного солнечного излучения на небе, поскольку распределение солнечной освещенности по небу трудно представить. адекватно.

Прямая и рассеянная составляющие солнечной радиации могут быть оценены с помощью эмпирических соотношений с помощью индекса четкости.

Некоторые из этих алгоритмов, требующие в качестве входных данных прямого нормального и рассеянного излучения на горизонтальной поверхности, могут давать очень разные оценочные результаты в разных местах [33].

Действительно, наиболее значительная причина ошибки в вычислении оптимального наклона и ориентации солнечной панели зависит от модели рассеянного солнечного излучения, которая используется.

Muneer [34] рекомендует модель, предложенную [35] для пустынь и тропиков: Для умеренного климата и мест вне тропиков можно использовать уравнение (5) из [36]: Ежедневное горизонтальное диффузное облучение и облучение прямым пучком также может быть получено с помощью (4) и (5).

3. Алгоритм максимизации глобального солнечного излучения на фиксированной наклонной поверхности

3.1. Случай изотропной диффузии

Глобальное солнечное излучение на наклонной поверхности состоит из ежедневного прямого солнечного излучения, рассеянного солнечного излучения и излучения, отраженного от земли.

Суточная солнечная радиация на наклонной поверхности для данного месяца может быть оценена следующим образом [9]: Ежедневное прямое излучение на наклонной поверхности может быть получено с помощью отношения среднего дневного прямого излучения на наклонной плоскости к таковому в горизонтальной плоскости и связанных с ним параметров [37]: где — наклон панели относительно горизонтальной плоскости, — азимут, — часовой угол Солнца, — широта, и — угол падения Солнца на рассматриваемую плоскость и зенитный угол Солнца, соответственно.

Если мы рассмотрим равномерное и изотропное распределение диффузного солнечного излучения по полусфере неба, то легко будет получено с помощью простого приближения [9]: Оценка отраженного от земли диффузного излучения зависит от. В большинстве исследований считается, что процесс отражения от земли является в идеале изотропным, и конкретный случай можно упростить следующим образом: где представляет собой коэффициент диффузного отражения земли (также называемый альбедо земли ).

Наконец, дневное глобальное солнечное излучение на склонах можно выразить как сумму (7), (9) и (10).

Глобальное солнечное излучение, падающее на наклонную поверхность, зависит от положения солнца на его дневной траектории (представленной солнечным углом) и от ориентации панели (представленной наклоном и азимутом).

Остальные величины, фигурирующие в (6), (7), (8), (9) и (10), зависят от местных условий и могут считаться фиксированными параметрами.

Предлагаемый здесь алгоритм основан на предположении, что дневное солнечное излучение, падающее на собирающую поверхность, является максимальным по углам, и, где — наклон панели относительно горизонтальной плоскости, — азимут, и — солнечный часовой угол соответственно.

Это физическое условие для максимизации солнечной радиации, получаемой солнечной панелью, может быть представлено математическими выражениями [8]: Их приложение к изотропной модели [9] дает следующие выражения [8]: Эта система уравнений может быть решена относительно углов, и [8]: Трансцендентные уравнения (13), (14) и (15) могут быть решены итерационными методами в отношении углов, и, которые обеспечивают, соответственно, оптимальный наклон и ориентацию солнечной панели, а также угловое положение панели. солнце в небе, где происходит максимальное увеличение солнечного излучения на панели.

3.2. Случай анизотропной диффузии

Рассеянное солнечное излучение влияет на эффективность большинства технологий солнечной энергии. Фактически, рассеивающие атмосферные процессы перераспределяют солнечную энергию из прямого луча в диффузное излучение. Фотовольтаические системы, как и плоские коллекторы, имеют особенность использовать как прямые, так и диффузные формы излучения, тогда как системы солнечных концентраторов могут использовать только прямое излучение.

К сожалению, планетарная сеть станций измерения рассеянного солнечного излучения оставляет желать лучшего, в то время как глобальные данные о солнечной радиации доступны для многих мест.

Тем не менее, эмпирические корреляции между диффузным и глобальным отношениями и диффузным и прямым солнечным излучением могут быть использованы для уменьшения ошибок в вычислении полусферического излучения на основе оценок прямого и рассеянного излучения, особенно в отношении условий неясного неба.

Помимо изотропной модели диффузного солнечного излучения, описанной в [9], было предложено несколько моделей для представления анизотропии диффузной составляющей с помощью эмпирических соотношений, которые должны модифицировать выражения (12) и относительные решения (13), (14) и (15).

Предположение, что диффузное излучение полностью исходит от солнечного диска, дает соотношение что является моделированием, противоположным изотропному из [9].

Ле Кер [38] и Хэй и Дэвис [39] предложили модель диффузной солнечной компоненты как комбинацию двух компонентов, то есть (9) и (16), где выражает степень анизотропии.

Это значение было предложено [38], тогда как [39] приняло отношение прямого земного излучения к внеземному излучению как степень анизотропии.

Клучер [40] предложил модель, в которой изотропная составляющая (изо) умножается на два фактора, которые представляют как околосолнечное, так и повышение яркости горизонта: где параметр выражает степень анизотропии как модулирующую функцию количества прямого излучения, принимаемого поверхностью (эта модель сводится к изотропной модели Лю-Жордана, если отношение диффузного излучения к глобальному близко к единице).

В литературе были предложены другие модели для определения анизотропии диффузного солнечного излучения с помощью некоторых коэффициентов, полученных на основе статистического анализа эмпирических данных для конкретных мест [41–43].

Тем не менее, здесь были учтены анизотропные модели [38–40], так как они легко применимы в любом месте. Кроме того, это широко проверенные модели, которые преобразуют полусферические данные на горизонтальной поверхности в полусферические данные на наклонной поверхности, вычисляя рассеянное солнечное излучение.

Математические условия (11), примененные к моделям [38, 39], дали следующие решения: Уравнения (19), (20) и (21) могут быть решены итерационными методами относительно углов β , γ и ω .Математические условия (11), примененные к модели из [40], представленной (18), давали следующие выражения: где Эта система уравнений может быть решена только с помощью итерационных методов.

4. Применение алгоритма максимизации к набору данных глобального горизонтального солнечного излучения

Данные, собранные в Европейском атласе солнечной радиации (доступном на Интернет-сайте HelioClim), были использованы для тестирования предложенного здесь алгоритма.

В частности, глобальная горизонтальная солнечная радиация относительно Триполи, Афин, Рима, Парижа, Лондона и Стокгольма, расположенных от 32 ° до 59 ° северной широты, была рассмотрена путем усреднения значений на ежемесячной основе с 1985 по 1989 год и был использован для этого моделирования.

Расчеты, и проводились каждый месяц, поскольку их изменением во времени нельзя пренебречь [44].

Значения склонения Солнца вычислялись в середине каждого месяца по уравнению Купера, которое также использовалось для расчета часового угла заката [37]. Ежедневное внеземное излучение на горизонтальной поверхности было вычислено в тот же день [27]; уравнение (5) из [39] использовалось как связь между и. Альбедо земли было зафиксировано на типичном значении.

Изотропная модель [9] и анизотропная модель [38–40] использовались для расчета диффузной солнечной компоненты.

Решения (14), (15), (20), (21), (23) и (24) дали значения и, подтверждая, что оптимальная ориентация солнечной панели — на юг, где на самом деле солнечный часовой угол в солнечный полдень должен быть равен нулю, как это определено.

Тем не менее, другие модели солнечной диффузной компоненты могут дать другие значения.

Оптимальные значения угла наклона, полученные из решений (13), (19), (22), указаны в таблицах 1, 2, 3, 4, 5 и 6.

9018 435 9153 915 9153 9153 915 9153 9153 915 915 9153 9153 915 915 9153 Солнечное склонение. (градус) Изотропная модель Модель Ле Кере Модель Хэя и Дэвиса Модель Клучера Значения SEM (градус) (МДж / м 2 (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) = −21.269 ​​ 50,7 12,44 55,3 13,05 53,3 12,73 57,0 18,54 1,17 1,26 46,0 17,59 48,7 21,56 0,95 0,87 = −2,819 33,7 22,54 3718 23,0 3718 23,50 61 35,8 23,18 37,4 24,06 0,72 0,28 = 9,415 21,9 27,08 24,3 27,08 24,3 24,3 0,45 0,42 = 18,792 12,9 29,26 14,3 30,16 13,8 29,83 13,6 27.56 0,25 0,50 = 23,314 8,6 30,92 9,5 31,53 9,2 31,34 9153 31,34 9153 918 10,6 31,92 11,4 32,55 11,2 32,39 10,9 30,00 0,15 0,50 = 13.784 18,4 30,71 19,8 31,58 19,4 31,35 19,4 28,77 0,25 0,55 0,25 0,55 0,25 0,55

31,2 26,43 32,0 25,90 0,50 0,22 = -9,599 40,9 20,16 44,0 20.99 43,0 20,69 44,9 23,73 0,75 0,69 = -19,148 48,5 13,26 9153 918 918 9180 918 918 918 918 918 918 9180 1,18 1,13 = −23,335 51,8 10,64 57,2 11,21 54,5 10,87 58,9 1635054 1,35 1,23

---

903 Солнечный склон. (градус) Изотропная модель Модель Ле Кере Модель Хэя и Дэвиса Модель Клучера Значения SEM (градус) (МДж / м 2 (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) = −21.269 ​​ 50,1 6,58 60,5 7,42 53,5 6,73 60,2 9,89 2,22 0,66 90 −315,22 0,66 90 −315,22 0,66 90 −3152 45,8 9,68 52,2 12,16 2,19 0,54 = −2,819 33,0 13,16 42,4 94 36,2 13,59 40,9 14,65 1,87 0,37 = 9,415 24,7 20,47 3018 9183 50 20,47 3018 9183 950 20,47 3018 9183 950 30,2 1,03 0,47 = 18,792 17,1 24,75 20,5 26,65 18,7 25,56 18,9 23.23 0,61 0,62 = 23,314 13,6 28,03 15,8 29,58 14,8 28,82 3 14,6 26350 28,82 3 14,6 26350 950 950 950 15,7 29,27 17,7 30,82 16,9 30,15 16,8 26,97 0,36 0,73 = 13.784 22,9 27,03 25,9 28,83 24,7 28,03 25,3 25,33 0,55 0,65 9155 0,65 34 9155 36,0 22,62 38,2 22,39 0,90 0,31 = -9,599 43,2 14,21 49,5 15.64 46,2 14,77 50,6 17,48 1,45 0,62 = -19,148 48,2 7,38 5818 9183 1018350 7,38 5818 9183 7,38 5818 9183 7,38 2,19 0,65 = -23,335 52,3 5,92 62,5 6,67 55,6 6,06 62,2 62,2 35 2,18 0,69

9152 9153 9153 9153 9153 9153 9153 915 915 915 9153333 Солнечный склон. (градусы) Изотропная модель Модель Ле Кере Модель Хэя и Дэвиса Модель Клучера Значения SEM (градусы) (МДж / м 2 ) ) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж) / м 2 ) = −21.269 ​​ 57,5 ​​ 6,93 64,6 7,93 60,4 7,21 65,8 11,47 1,66 0,91 1,66 0,91 52,7 11,02 58,1 14,38 1,71 0,74 = −2,819 40,1 16,05 46,7 .15 43,1 16,82 47,4 18,12 1,47 0,44 = 9,415 28 20,02 34,3 50 34,3 50 34,3 50 34,3 50 1,22 0,56 = 18,792 20,2 24,07 24,6 26,66 22,2 25,07 23 22.46 0,79 0,76 = 23,314 16,8 27,14 20 29,45 18,4 28,17 18,5 2415350 18,5 2150 19 28,82 21,9 31,08 20,7 29,98 20,9 26,21 0,52 0,90 = 13.784 26,5 26,82 30,1 29,19 28,6 28,07 29,7 24,99 0,70 0,78 0,78 0,78 39,2 20,80 42,3 20,75 1,15 0,40 = -9,599 49 15,29 53,6 16.83 51,6 16,04 55,3 19,35 1,17 0,76 = -19,148 55,7 8,01 62,6 918 8,01 62,6 918 62,6 918 950 950 950 1,63 0,90 = −23,335 61,5 7,05 66,7 7,94 64 7,38 68,4 12.76 1,31 1,15

7,53 9155 9153000 903 1750 50 903 1750 95015 Солнечный склон. (градусы) Изотропная модель Модель Ле Кере Модель Хэя и Дэвиса Модель Клучера Значения SEM (градусы) (МДж / м 2 ) ) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж) / м 2 ) = −21.269 ​​ 56,7 3,98 68,1 4,94 59,9 4,10 66,5 6,54 2,33 0,51 0,51 9155 50,4 6,25 58 8,21 2,74 0,44 = −2,819 38,3 10,30 50,2 12.66 41,7 10,73 48,3 11,94 2,41 0,47 = 9,415 28,7 15,74 38189 18950 9,74 3818 3818 3 1,80 0,64 = 18,792 20,4 17,66 28,4 21,00 22,8 18,36 24,5 16.94 1,45 0,76 = 23,314 18,3 22,16 23,9 25,46 20,4 23,11 21,2350 23,11 21,2350 21,2 21,1 24,83 25,9 28,13 23,3 26,05 24,2 22,76 0,87 0,97 = 13.784 27,8 21,73 33,9 25,06 30,5 22,92 32,9 20,72 1,17 0,80 1,17 0,80 0,80 0,80 42 18,50 46,2 18,67 1,46 0,49 = -9,599 48,7 10,22 57,1 12.14 52 10,75 57,9 13,32 1,88 0,60 = -19,148 58,1 5,93 66,3 718350 5,93 66,3 718350 95015 66,3 718350 95015 66,3 66,3 718350 950 1,83 0,73 = −23,335 62,6 4,31 70,3 5,22 65,3 4,50 70,6 8.02 1,70 0,74

34 34 147,17 147,17 147,17 Солнечн. (градусы) Изотропная модель Модель Ле Кере Модель Хэя и Дэвиса Модель Клучера Значения SEM (градусы) (МДж / м 2 ) ) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж) / м 2 ) = −21.269 ​​ 61,8 2,24 73,8 3,10 64,7 2,32 70,6 4,00 2,36 0,36 0,36 55,5 4,56 63 6,26 2,80 0,41 = −2,819 41,4 7,79 55,9 10.46 44,9 8,14 52,6 9,26 2,90 0,52 = 9,415 32 13,31 44 9,31 44 9,31 2,33 0,80 = 18,792 25,8 18,88 34,6 23,65 28,6 19,96 31,7 17.86 1,45 1,09 = 23,314 20,7 17,87 29,9 22,55 23,1 18,71 25183 16350 18,71 25183 16350 18,71 25183 16350 21,7 16,61 31,7 21,20 24,2 17,37 26,7 15,83 1,84 1,03 = 13.784 28,2 14,54 39,6 18,85 31,2 15,29 35,8 14,44 2,17 0,90 0,90 0,90 0,90 42,6 11,63 49,3 12,24 2,43 1,13 = -9,599 54,9 8,65 62,9 10.84 58 9,23 63,8 11,86 1,82 1,13 = -19,148 63,1 3,68 4,8 72,0 903 915 950 72,0 903 950 72,0 903 950 1,85 1,06 = −23,335 64,2 1,73 75,8 2,41 66,8 1,78 72,2 3.31 2,26 0,32

9153 Солнечн. (градус) Изотропная модель Модель Ле Кере Модель Хэя и Дэвиса Модель Клучера Значения SEM (градусы) (МДж / м 2 ) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) (градус) (МДж / м 2 ) = −21.269 ​​ н.у. н.у. н.у. н.у. н.у. н.у. = -13,289 67,1 5,18 73,2 6,99 69,5 5,65 73,8 8,79 1,37 8,79 1,37 1,37 0 1,37 0 1,37 63,1 13,77 57,9 11,15 63,8 12.56 1,88 0,68 = 9,415 43,1 18,64 51,3 24,32 46,4 20,37 3 183 18350 20,37 3 51,850 950955 33,0 21,99 41,8 29,10 36,2 23,88 40,7 19,95 1,77 1,70 = 23.314 29,5 25,39 37,3 32,92 32,4 27,54 35,9 22,19 1,52 1,95 1,52 1,95 1,52 1,95 915,89	32,9	23,59	37,0	19,68	1,78	1,75
= 13,784	33,8	14,17	46.5	20,12	37,2	15,15	43,4	13,98	2,50	1,25
= 2,217	46,3	10,25 903	50 56,9	11,52	2,44	0,79
= -9,599	60,5	5,65	69,5	7,93	63,5	6,09	69.3	8,25	1,92	0,56
= −19,148	н.у.		н.у.		н.у.		н.у.		н.у.	н.у.
= −23,335	н.у.		н.у.		н.у.		н.у.		н.у.	н.у.

Соответствующее среднемесячное дневное глобальное солнечное излучение (измеренное в МДж / м ² ), собираемое поверхностью, наклоненной на каждое значение β , указано в таблицах 1–6 , также.Такое значение можно считать представительным для эффективности преобразования фотоэлектрического модуля из-за линейной зависимости от интенсивности солнечного излучения [45].

Результаты привели к следующим соображениям. (1) Было подтверждено, что оптимальные значения угла наклона солнечных панелей, определенные для зимних месяцев, сильно отличаются от значений, рекомендованных для летних месяцев. (2) Значение было подтверждено как оптимальное. значение ориентации для солнечной панели. (3) Разногласия между моделями диффузного солнечного излучения в результате были актуальны для зимних месяцев (представленных солнечными склонениями и, соответствующими первым трем и последним трем строкам таблиц 1–6) и привело к увеличению с увеличением широты.

Кроме того, оптимальные значения угла наклона были усреднены для каждого месячного склонения Солнца и представлены как функция широты в Таблице 7. Полученные средние значения углов наклона в значительной степени связаны с широтами. Была изучена корреляция между этими двумя наборами переменных с применением линейной зависимости для прогнозирования значения оптимального угла наклона для данной географической широты.

β () β () β () β () 5 936 936 936 936 () 0 0 β () β () Коэффициенты Корреляция 54.07 56,08 62,07 62,80 67,72 — 31,33 0,68 0,953 46,45 48,25 903 48,25 48,25 950 0,944 35,97 38,13 44,32 44,62 48,70 59,87 0.84 0,957 23,37 27,70 31,57 33,55 38,03 48,15 0,87 0,975 0,87 0,975 0,87 0,975 9153 9155

9185 9155 37,92 0,87 0,978 9,05 14,70 18,42 20,95 24.73 33,77 0,87 0,985 11,03 16,78 20,62 23,62 26,08 34,67 34,67 34,67 9183 28,72 31,27 33,70 40,22 0,75 0,989 31,15 36,40 39.95 43,22 45,53 52,75 0,77 0,993 43,20 47,37 52,37 53,93 5918350 52,37 53,93 9153 9153 53,9350 9153 51,90 54,13 60,20 63,10 68,07 — 0,84 0,977 55.60 58,15 65,15 67,20 69,75 — 0,76 0,968

---

по методу регрессии по наименьшему квадрату , чтобы сделать сумму квадратов разностей между ординатами точек и точек на прямой как можно меньшей. Был рассчитан коэффициент корреляции «» переменных, который определяется как их ковариация (которая измеряет, как две переменные линейно связаны), деленная на произведение их индивидуальных стандартных отклонений.Кроме того, считался доверительный интервал, чтобы узнать, насколько точна регрессия.

Линейные регрессии с 95% доверительным интервалом обеспечили коэффициенты корреляции от 0,944 до 0,993, указанные в последнем столбце таблицы 7 (более высокие значения корреляции были обнаружены для летних месяцев). Две типичные подгонки для двух склонений Солнца показаны на рисунках 1 (a) и 1 (b).

Этот результат показывает, что оптимальный угол наклона солнечной панели может быть легко получен как функция географической широты с помощью коэффициентов и линейной регрессии.Коэффициенты и, полученные с помощью регрессии, зависят от использованного склонения Солнца.

Кроме того, применение алгоритма показало, что различия между значениями угла наклона, вычисленными с использованием различных моделей диффузного солнечного излучения, увеличиваются с увеличением географической широты, что предполагает дальнейшие эмпирические корреляции между диффузным и глобальным отношениями и диффузным и прямым солнечная радиация должна быть исследована, особенно в высоких широтах.

Наконец, стандартная ошибка среднего (SEM) углов наклона и среднемесячного значения дневных значений глобального солнечного излучения была вычислена и указана в последнем столбце таблиц 1–6 для количественной оценки разногласий между различными здесь использованы модели диффузного солнечного излучения.

Средние значения этих значений SEM были рассчитаны отдельно для летних и зимних месяцев и представлены в таблице 8.

Широта (градусы) Средние значения значений SEM Летние месяцы Зимние месяцы 32.95 0,30 0,44 1,01 0,91 37,96 0,64 0,57 2,01 0,59 0,59 0,59 0,59 902 48,85 1,26 0,75 2,15 0,58 51,53 2,02 0,92 2,33 0,46 28 1,96 1,44 н.у. н.у. Коэффициент корреляции 0,956 0,935 0,835 −0,789

Значительная корреляция между средними значениями SEM и средними значениями для летних месяцев этих месяцев была обнаружена. Фактически, линейная регрессия с 95% доверительным интервалом предоставила коэффициенты корреляции, а также для углов наклона и среднемесячного значения дневных значений глобального солнечного излучения, соответственно.Эти линейные регрессии представлены на рисунках 2 (а) и 2 (б).

Что касается зимних месяцев, были обнаружены более низкие корреляции (см. Таблицу 8). Тем не менее, значения, полученные для зимних месяцев, можно считать менее надежными, поскольку уменьшение интенсивности прямого и рассеянного солнечного излучения в зимние месяцы приводит к увеличению относительной ошибки для оценки углов наклона и среднемесячного дневного глобального солнечного излучения. значения.

5. Выводы

Предложенный здесь метод максимизации глобального солнечного излучения позволил учесть набор уравнений, которые можно решить относительно наклона β и азимута γ собирающей поверхности и к солнечному часовому углу ω .Предложенный алгоритм был применен к некоторым моделям диффузного солнечного излучения с использованием данных глобального горизонтального солнечного излучения из Европейского атласа солнечной радиации. Относительные уравнения предоставили набор углов β , γ и ω в зависимости от других физических параметров. Была подтверждена лучшая ориентация солнечных панелей на юг и большая зависимость оптимального угла наклона от времени, что предполагает использование полужестких панелей на строительных конструкциях.

Решения системы уравнений обеспечили углы наклона и среднемесячные суточные значения глобального солнечного излучения, строго связанные с использованной моделью диффузного солнечного излучения.

Полученные вычисленные углы наклона были существенно связаны со значением широты, потому что линейные регрессии с 95% доверительным интервалом обеспечивали коэффициенты корреляции в диапазоне от 0,944 до 0,993. Этот результат позволяет оценить оптимальный угол наклона солнечной панели в зависимости от широты с помощью линейной регрессии, коэффициенты которой зависят от данных глобального горизонтального солнечного излучения.

Тем не менее, соответствующие различия между среднемесячным значением дневной глобальной солнечной радиации и значениями угла наклона, полученными с использованием различных моделей рассеянного солнечного излучения, были выявлены при моделировании, выполненном отдельно для летних и зимних месяцев.

Стандартная ошибка среднего таких значений привела к значительному увеличению с увеличением широты в летние месяцы, что привело к выводу, что значения, недостоверные для оптимального угла наклона солнечной панели, могут быть получены с помощью моделей рассеянного солнечного излучения при высоких температурах.