Стереометрия. Площадь сечения через площадь проекции сечения.
Если сечение сложной формы, то не стоит пытаться найти его площадь “в лоб”. Умный гору обойдет… И мы обойдем: определим площадь проекции сечения (обычно это очень просто) и угол наклона плоскости сечения к плоскости основания. Потом воспользуемся известной формулой. Но об этом – дальше.
Задача 1. В прямоугольном параллелепипеде  с ребрами
с ребрами  ‚
‚  и
и 
 и
и  -середины ребер
-середины ребер  и
и  соответственно. Плоскость
соответственно. Плоскость  пересекает ребро
пересекает ребро  в точке
в точке  .
.а) Докажите, что  ;
;
б) Найдите площадь сечения этого параллелепипеда плоскостью  .
.

Рисунок 1 – к задаче 1
Построим сечение. Построим прямую 
 и
и  принадлежат одной грани. Построим прямую
принадлежат одной грани. Построим прямую  и найдем точку пересечения прямой
и найдем точку пересечения прямой  и прямой
и прямой  – точку
– точку  .
. 
Рисунок 2 – к задаче 1
Эта точка принадлежит как плоскости грани  , так и плоскости грани
, так и плоскости грани  . Проведем прямую
. Проведем прямую  и определим точку пересечения этой прямой с ребром
и определим точку пересечения этой прямой с ребром 
 .
. 
Рисунок 3 – к задаче 1
Построим линии, по которым сечение «режет» грани параллелепипеда:  .
.

Рисунок 4 – к задаче 1
Теперь построим прямую 
 – точка
– точка  пересечения лежит в плоскости верхней грани, и это позволяет соединить ее с точкой
пересечения лежит в плоскости верхней грани, и это позволяет соединить ее с точкой  . Теперь найдем место пересечения отрезка
. Теперь найдем место пересечения отрезка  с ребром
с ребром 
 , и можно обводить и штриховать сечение:
, и можно обводить и штриховать сечение: 
Рисунок 5 – к задаче 1
Докажем пункт а). Рассмотрим треугольники  и
и  . Они подобны, так как образованы параллельными прямыми:
. Они подобны, так как образованы параллельными прямыми: 
 , то коэффициент подобия этих треугольников –
, то коэффициент подобия этих треугольников –  . Тогда
. Тогда  . Так как треугольники
. Так как треугольники  и
и 
 , то
, то  . Но треугольники
. Но треугольники  и
и  равны по 2 признаку, следовательно,
равны по 2 признаку, следовательно,  , или
, или  , то есть
, то есть  .
.б) Определим площадь сечения. Для этого можно определить площадь проекции этого сечения, и косинус угла между плоскостью и основанием параллелепипеда. Сначала найдем площадь проекции. Отрежем два треугольника от основания параллелепипеда, тогда оставшееся – и есть площадь проекции (многоугольник  – выделено голубым цветом).
– выделено голубым цветом).

Рисунок 6 – к задаче 1
Площадь основания параллелепипеда равна 12, отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,

Отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,

Тогда площадь проекции равна

Теперь найдем угол наклона плоскости сечения к плоскости основания, вернее, его косинус. Нужно найти косинус угла – или любую другую тригонометрическую функцию – угла  . Рассмотрим треугольник
. Рассмотрим треугольник  . Он прямоугольный, катет
. Он прямоугольный, катет  (равен высоте параллелепипеда). Длина отрезка
(равен высоте параллелепипеда). Длина отрезка  может быть найдена из треугольника
может быть найдена из треугольника  :
:

По ранее доказанному  ,
,  .
.


Тогда

Площадь сечения равна

Ответ:  .
.
Задача 2. В правильной четырехугольной призме  сторона
сторона  основания равна 6, а боковое ребро
основания равна 6, а боковое ребро  равно
равно  . На ребрах
. На ребрах  и
и  отмечены точки
отмечены точки  и
и  соответственно, причем
соответственно, причем  .
.
а) Пусть  – точка пересечения плоскости
– точка пересечения плоскости  с ребром
с ребром  . Докажите, что
. Докажите, что  – квадрат;
– квадрат;
б) Найдите площадь сечения призмы плоскостью  .
.

Рисунок 1 – к задаче 2
Проведем прямую  и через точку
и через точку  – параллельную ей прямую, так как плоскость сечет противоположные грани параллелепипеда (прямой призмы) по параллельным прямым:
– параллельную ей прямую, так как плоскость сечет противоположные грани параллелепипеда (прямой призмы) по параллельным прямым:

Рисунок 2 – к задаче 2
Найдем точку пересечения прямой  и
и  – точку
– точку  . Эта точка принадлежит плоскости грани
. Эта точка принадлежит плоскости грани  . Поэтому ее можно соединить с точкой
. Поэтому ее можно соединить с точкой  отрезком, который пересечет ребро
отрезком, который пересечет ребро  в точке
в точке  . Найдем точку пересечения прямой
. Найдем точку пересечения прямой  и
и  – точку
– точку  . Эта точка принадлежит плоскости грани
. Эта точка принадлежит плоскости грани  . Поэтому ее можно соединить с точкой
. Поэтому ее можно соединить с точкой  отрезком, который пересечет ребро
отрезком, который пересечет ребро  в точке
в точке  .
.

Рисунок 3 – к задаче 2

Рисунок 4 – к задаче 2
Соединяя точки  ,
,  ,
,  ,
,  ,
,  ,
,  , получим искомое сечение.
, получим искомое сечение.
Докажем, что  – квадрат.
– квадрат.

Рисунок 5 – к задаче 2
Так как отрезки  и
и  принадлежат одной плоскости (плоскости сечения) и одновременно параллельным плоскостям верхнего и нижнего оснований призмы, то они параллельны. Также
принадлежат одной плоскости (плоскости сечения) и одновременно параллельным плоскостям верхнего и нижнего оснований призмы, то они параллельны. Также  .
.
 и
и  – диагонали прямых правильных призм со стороной основания 1 и высотой
– диагонали прямых правильных призм со стороной основания 1 и высотой  . Тогда
. Тогда

Получается,  – как минимум, ромб. И по признаку параллелограмма, так как противоположные стороны попарно равны, то
– как минимум, ромб. И по признаку параллелограмма, так как противоположные стороны попарно равны, то  – квадрат.
– квадрат.
б) Определим площадь сечения. Для этого можно определить площадь проекции этого сечения, и косинус угла между плоскостью и основанием параллелепипеда. Сначала найдем площадь проекции. Отрежем два треугольника от основания параллелепипеда, тогда оставшееся – и есть площадь проекции (многоугольник  – выделено фиолетовым цветом).
– выделено фиолетовым цветом).

Рисунок 6 – к задаче 2
Площадь основания призмы равна 36, отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,

Отрезаем треугольник  :
:  по условию,
по условию,  по доказанному отношению из пункта а). Следовательно,
по доказанному отношению из пункта а). Следовательно,

Тогда площадь проекции равна

Теперь найдем угол наклона плоскости сечения к плоскости основания, вернее, его косинус. Нужно найти косинус угла – или любую другую тригонометрическую функцию – угла  . Рассмотрим треугольник
. Рассмотрим треугольник  . Он прямоугольный, катет
. Он прямоугольный, катет  (равен высоте параллелепипеда). Длина отрезка
(равен высоте параллелепипеда). Длина отрезка  может быть найдена из треугольника
может быть найдена из треугольника  :
:

По ранее доказанному  ,
,  .
.


Тогда

Площадь сечения равна

Ответ:  .
.
| Фигура | Формула вычисления площади | Примечания | Вычислить площадь |
|---|---|---|---|
| Квадрат | $$a^2$$ | a длина стороны квадрата. | |
| Равносторонний треугольник | $$\frac{\sqrt{3}}{4}a^2$$ | a – длина одной из сторон | |
| Треугольник | $$\sqrt{s(s-a)(s-b)(s-c)}$$ | где s = 1/2 (a + b + c), a,b,c – длины сторон треугольника | |
| $$\frac{1}{2}b\cdot h_b$$ | где b – длина стороны треугольника hb – высота, проведённая на сторону b | ||
| $$\frac{1}{2} a b \sin \gamma $$ | где a и b – длина сторон треугольника [math]\gamma[/math] – угол между ними в ° | ||
| Правильный шестиугольник | $$\frac{3\sqrt{3}}{2}s^2$$ | s – сторона шестиугольника | |
| Правильный восьмиугольник | $$2\left(1+\sqrt{2}\right)s^2$$ | s – сторона восьмиугольника R – радиус описанной окружности $$s={R\over\sqrt{1+{\sqrt{2}/2}}} ≈ {R\over 1.3066}$$ | |
| Прямоугольник | $$a\cdot b$$ | a и b стороны прямоугольника (длина и ширина) | |
| Параллелограмм | $$b\cdot h$$ | b – длина одной из основ параллелограмма h – высота параллелограмма | |
| Трапеция | $$\frac{a+b}{2}\cdot h $$ | a и b длины параллельных сторон, а h – высота (расстояние между параллельными сторонами) | |
| Правильный многоугольник (это многоугольник, у которого все углы и все стороны равны между собой) | $$\frac{ns^2} {4 \cdot \tan(\pi/n)} $$ | s -длина стороны, а n число сторон. | |
| Круг | $$\pi r^2 \text{ или } \frac{\pi d^2}{4} $$ | r – радиус, а d – диаметр | |
| Эллипс | $$\pi ab $$ | a и b – большая и малая полуоси эллипса, соответственно. | |
| Сектор (часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга) | $$\frac{1}{2} r^2 \theta $$ | r и [math]\theta[/math] – радиус и угол (в радианах), соответственно | |
| $$\frac{1}{2} r^2 \frac{\theta \pi}{180} $$ | r и [math]\theta[/math] – радиус и угол (в ° ), соответственно |
особенности величины, как найти её для круга
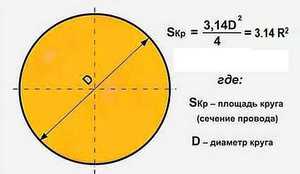 В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
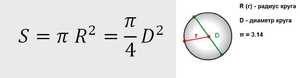
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
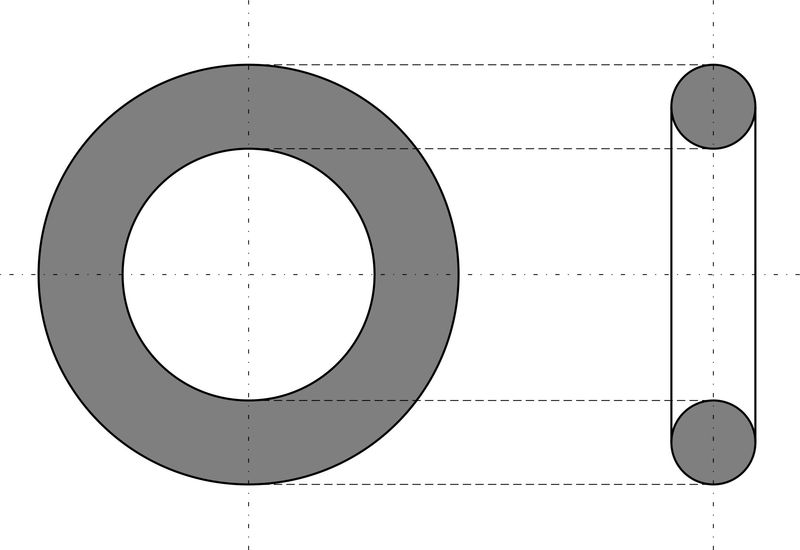
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Площадь сечения треугольника формула — Морской флот
Открытый банк заданий по теме площадь сечения. Задания C2 из ЕГЭ по математике (профильный уровень)
Задание №1186
Условие
В правильном тетраэдре DABC с ребром 5 на рёбрах AD , BD и AC выбраны точки K , L и M соответственно так, что KD=MC=2, LD=4.
а) Постройте сечение тетраэдра плоскостью KLM .
б) Найдите площадь этого сечения.
Решение
а) Так как AK=AM=5-2=3, то riangle AKM равнобедренный.
Так как в этом равнобедренном треугольнике angle KAM=60^<circ>, то он равносторонний, то есть
KM=3. Тогда KM parallel DC, так как равны соответственные углы при прямых KM , DC и секущей AD .
Построим LN parallel DC. Так как в этом случае LN parallel KM, то точки K , L , N и M лежат в одной плоскости, то есть трапеция KLNM есть искомое сечение.
б) 1. riangle BLN sim riangle BDC, так как LN parallel DC. Следовательно, riangle BLN является равносторонним и LN=BN=BL =BD-LD=5-4=1.
2. riangle DKL= riangle CMN, так как DK=CM =2, DL=CN=4 и angle KDL=angle MCN=60^<circ>. Значит, KL=MN и KMNL — равнобедренная трапеция.
Опустим в ней высоту LH . Отсюда, KH =frac2=frac<3-1>2=1.
3. По теореме косинусов для riangle KDL получим:
KL^2= KD^2+DL^2-2cdot KDcdot DLcdot cos 60^<circ>= 2^2+4^2-2cdot 2cdot 4cdot frac12= 12.
4. По теореме Пифагора LH= sqrt = sqrt <12-1>= sqrt <11>.
5. S_= frac12(KM+LN)cdot LH= frac12(3+1)cdot sqrt <11>= 2sqrt <11>.
Ответ
Задание №1185
Условие
В правильной четырёхугольной призме ABCDA_1B_1C_1D_1 сторона основания равна 9 , боковое ребро равно 14 . Точка K принадлежит ребру A_1B_1 и делит его в отношении 2:7, считая от вершины A_1.
а) Докажите, что сечение призмы плоскостью, проходящей через точки A , C и K , является равнобедренной трапецией.
б) Найдите площадь этого сечения.
Решение
а) Плоскость сечения пересекает плоскость верхнего основания по прямой, проходя-щей через точку K и параллельной AC (по свойству параллельности плоскостей). Тогда плоскость AKC пересекает ребро B_1C_1 в точке L так, что KL parallel AC. Следовательно, искомым сечением будет трапеция AKLC .
KB_1parallel AB, B_1Lparallel BC, KLparallel AC. Значит, треугольники KB_1L и ABC подобны и являются равнобедренными прямоугольными треугольниками. Тогда KB_1=B_1L и A_1K=C_1L. Треугольники AA_1K и CC_1L равны, следовательно, AK=CL и трапеция AKLC — равнобедренная.
б) Найдём площадь трапеции AKLC .
A_1K=frac29A_1B_1 =frac29cdot 9=2.
Из riangle AA_1K,, AK = sqrt = sqrt <14^2+2^2>= 10sqrt 2.
AC=ABsqrt 2=9sqrt 2; KL =frac79AC=frac79cdot 9sqrt 2=7sqrt 2.
Так как трапеция AKLC — равнобедренная, имеем
Из riangle AKH,, KH= sqrt = sqrt <200-2>= sqrt <198>.
S_=frac2cdot KH,= 8sqrt 2cdot sqrt <198>=48sqrt <11>.
Ответ
Задание №1180
Условие
В правильной четырёхугольной призме ABCDA_1 B_1C_1 D_1 сторона основания равна 7 , а боковое ребро — 12 . На рёбрах A_1D_1, C_1D_1 и CB взяты точки F, К, L соответственно так, что A_1F=C_1K=CL=3.
а) Пусть P — точка пересечения плоскости FKL с ребром AB . Докажите, что FKLP — прямоугольник.
б) Найдите площадь сечения призмы плоскостью FKL.
Решение
а) Найдём положение точки P . Эта точка пересечения плоскости FKL и ребра AB, лежащего в плоскости ABCD.
Плоскость ABCD параллельна плоскости A_1B_1C_1D_1, в которой лежит отрезок KF. Плоскость FKL пересекает параллельные плоскости ABCD и A_1B_1C_1D_1 по параллельным прямым, отсюда KF parallel LP. Прямоугольные треугольники KD_1F и LBP равны по катету и острому углу D_1F=LB=4 и angle D_1FK=angle BLP как острые с соответственно параллельными сторонами).
Чтобы доказать, что четырёхугольник FKLP — прямоугольник, найдём длины его сторон и диагонали.
PF= LK = sqrt = sqrt <9+144+9>= sqrt <162>= 9sqrt 2. Противоположные стороны четырёхугольника попарно равны, значит, это параллелограмм. Проведём A_1A_2 parallel LF, тогда LF= A_1A_2 = sqrt <(LB-FA_1)^2+AB^2+AA_1^2>= sqrt <(BP-C_1K)^2+CB^2+CC_1^2>= PK. Диагонали параллелограмма равны, следовательно, FKLP — прямоугольник.
б) Пусть Q и R — точки пересечения прямой KF и прямых B_1C_1 и A_1B_1. Проведём прямые RL и QP , они пересекут рёбра CC_1 и AA_1 в точках M и N соответственно. Тогда RC_1=KC_1=CL, поэтому можно доказать, что равны треугольники RC_1M и MCL. Прямая RL , а значит, и плоскость FKL пересекают ребро CC_1 в его середине — точке M . Аналогично плоскость FKL пересекает ребро AA_1 в его середине —точке N .
В диагональном сечении CC_1A_1A, которое является прямоугольником, отрезок MN — средняя линия. В прямоугольнике MCAN противоположные стороны равны: MN=CA=7sqrt 2.
Сечение FKMLPN состоит из двух равных трапеций MKFN и MLPN , причём
мы доказали, что LK perp KF и LK perp LP. Высота каждой из этих трапеций равна frac2=frac<9sqrt 2>2.
S_< ext<сечения>>= 2S_= 2cdot frac2cdot frac2= (4sqrt 2+7sqrt 2)cdot frac<9sqrt 2>2= 99.
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR 2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
где 2а – значение хорды, расчета площади поперечного сечения.
 В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
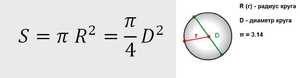
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
расчет поперечного сечения, как рассчитать, как найти проходное сечение
Содержание:
Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.

Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
S=π×R2, где
π – постоянное число, равное 3,14;
R – величина радиуса;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.

В результате вычисления производятся так:
S=π×(D/2-N)2, где
D – значение внешнего сечения трубы;
N – толщина стенок.
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.

Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N)2=3,14×(1/2-0,01)2=0,754 м2.
Физические характеристики труб
Стоит знать, что показатели площади поперечного сечения трубы напрямую влияют на скорость транспортировки газообразных и жидких веществ. Поэтому крайне важно заложить в проект трубы с правильным сечением. Кроме того, на выбор диаметра трубы будет влиять еще и рабочее давление в трубопроводе. Читайте также: «Как посчитать площадь трубы – способы и формулы расчета».

Также в процессе проектирования трубопроводов стоит учитывать химические свойства рабочей среды, а также ее температурные показатели. Даже если вы знакомы с формулами, как найти площадь сечения трубы, стоит изучить дополнительный теоретический материал. Так, информация относительно требований к диаметрам трубопроводов под горячее и холодное водоснабжение, отопительные коммуникации или транспортировку газов, содержатся в специальной справочной литературе. Значение имеет также сам материал, из которого произведены трубы.
Выводы
Таким образом, определение площади сечения трубы является очень важным, однако, в процессе проектировки нужно обращать внимание на характеристики и особенности системы, материалы трубных изделий и их прочностные показатели.
Площадь сечения. Задание С2
В последнее время в вариантах для подготовки к ЕГЭ по математике в Задании С2 часто стали появляться задачи на нахождение площади сечения. Рассмотрим решение такой задачи:
В прямоугольном параллелепипеде 
 ,
,  . Сечение параллелепипеда проходит через точки
. Сечение параллелепипеда проходит через точки  и
и  и образует с плоскостью
и образует с плоскостью  угол
угол  . Найдите площадь сечения.
. Найдите площадь сечения.
Как мы уже видели, часто бывает удобно находить площадь сечения через площадь его ортогональной проекции.
Нахождение площади треугольника через площадь его ортогональной проекции легко иллюстрируется таким рисунком:
 — высота треугольника
— высота треугольника  ,
,  — высота треугольника
— высота треугольника  , который является ортогональной проекцией треугольника
, который является ортогональной проекцией треугольника  . Из прямоугольного треугольника
. Из прямоугольного треугольника  :
:  .
.
Площадь треугольника  равна
равна  .
.
Площадь треугольника  равна
равна  .
.
Cледовательно, площадь треугольника  равна площади треугольника
равна площади треугольника  деленной на косинус угла между плоскостями треугольника
деленной на косинус угла между плоскостями треугольника  и треугольника
и треугольника  , который является ортогональной проекцией треугольника
, который является ортогональной проекцией треугольника  :
:

Поскольку площадь любого многоугольника можно представить в виде суммы площадей треугольников, площадь многоугольника равна площади его ортогональной проекции на плоскость деленной на косинус угла между плоскостями многоугольника и его проекции.
Используем этот факт для решения задачи:
В прямоугольном параллелепипеде 
 ,
,  .Сечение параллелепипеда проходит через точки
.Сечение параллелепипеда проходит через точки  и
и  и образует с плоскостью
и образует с плоскостью  угол
угол  . Найдите площадь сечения.
. Найдите площадь сечения.
План решения такой:
А) Строим сечение.
Б) Находим его ортогональную проекцию на плоскость основания.
В) Находим площадь ортогональной проекции.
Г) Находим площадь сечения.
Итак.
1. Сначала нам нужно построить это сечение.
Очевидно, что отрезок  принадлежит плоскости сечения и плоскости основания, то есть принадлежит линии пересечения плоскостей:
принадлежит плоскости сечения и плоскости основания, то есть принадлежит линии пересечения плоскостей:
Угол между двумя плоскостями — это угол между двумя перпендикулярами, которые проведены к линии пересечения плоскостей и лежат в этих плоскостях.
 . Пусть точка
. Пусть точка  — точка пересечения диагоналей основания.
— точка пересечения диагоналей основания.  — перпендикуляр к линии пересечения плоскостей, который лежит в плоскости основания:
— перпендикуляр к линии пересечения плоскостей, который лежит в плоскости основания:
2. Определим положение перпендикуляра, который лежит в плоскости сечения. (Помним, что если прямая перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Ищем наклонную по ее проекции (  ) и углу между проекцией и наклонной). Найдем тангенс угла
) и углу между проекцией и наклонной). Найдем тангенс угла  между
между  и
и  :
:


 , следовательно, угол
, следовательно, угол  между плоскостью сечения и плоскостью основания больше, чем между
между плоскостью сечения и плоскостью основания больше, чем между  и
и  . То есть сечение расположено как-то так:
. То есть сечение расположено как-то так:


 — точка пересечения
— точка пересечения  и
и 
 ||
|| .
.
Итак, вот наше сечение:
3. Найдем проекцию сечения  на плоскость основания. Для этого найдем проекции точек
на плоскость основания. Для этого найдем проекции точек  и
и  .
.
Четырехугольник  — проекция сечения
— проекция сечения  на плоскость основания.
на плоскость основания. 
4. Найдем площадь четырехугольника  . Для этого из площади треугольника
. Для этого из площади треугольника  вычтем площадь треугольника
вычтем площадь треугольника 
Найдем площадь треугольника  . Треугольник
. Треугольник  подобен треугольнику
подобен треугольнику  . Найдем коэффициент подобия. Для этого рассмотрим треугольники
. Найдем коэффициент подобия. Для этого рассмотрим треугольники  и
и  :
:
 . Следовательно,
. Следовательно,  и площадь треугольника
и площадь треугольника  составляет
составляет  площади треугольника
площади треугольника  (отношение площадей подобных фигур равно квадрату коэффициента подобия).
(отношение площадей подобных фигур равно квадрату коэффициента подобия).
Тогда площадь четырехугольника  равна
равна  площади треугольника
площади треугольника  и равна
и равна

5. Теперь найдем  .
.

6. И, наконец, получаем: 
Ответ: 112
И.В. Фельдман, репетитор по математике.


площадь поперечного сечения — это… Что такое площадь поперечного сечения?
- площадь поперечного сечения
3.5 площадь поперечного сечения (cross-sectional area): Площадь, которую нужно рассматривать после разрушения или разрезания.
3.6 площадь поперечного сечения (cross-sectional area): Площадь, которую нужно рассматривать после разрушения или разрезания.
1 — направление рентгеновского излучения; 2 — элемент объема с 4 порами; 3 — шестислойная толщина;
Рисунок 1 — Рентгенографические пленки образцов с идентичной распространенностью пор на единицу объема
Смотри также родственные термины:
3.7 площадь поперечного сечения арматуры Fa, мм2: Площадь поперечного сечения равновеликого по массе круглого гладкого образца, определяется по формуле
(1)
где т — масса образца, г;
l -длина образца, мм.
Определения термина из разных документов: площадь поперечного сечения арматуры Fa, мм2
Площадь поперечного сечения болта (шпильки) по внутреннему диаметру резьбы, мм2
fб
Определения термина из разных документов: Площадь поперечного сечения болта (шпильки) по внутреннему диаметру резьбы, мм2
Площадь поперечного сечения кольца жесткости, мм2 (см2)
Ак
Площадь поперечного сечения образца после разрыва Fк
Минимальная площадь поперечного сечения рабочей части образца после разрыва
Определения термина из разных документов: Площадь поперечного сечения образца после разрыва Fк
Площадь поперечного сечения распорного кольца, мм2 (см2)
Fк
3.21 площадь поперечного сечения трубопровода «в свету»: Площадь полости поперечного сечения трубопровода (ограниченная внутренним диаметром трубы).
Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.
- Площадь поперечного кольца жесткости, мм2
- площадь поперечного сечения арматуры Fa, мм2
Смотреть что такое «площадь поперечного сечения» в других словарях:
площадь поперечного сечения — A — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы A EN cross sectional area … Справочник технического переводчика
площадь поперечного сечения — skerspjūvio plotas statusas T sritis fizika atitikmenys: angl. cross sectional area; sectional area vok. Querschnitsfläche, f rus. площадь поперечного сечения, f pranc. aire de la section, f; aire de la section transversale, f … Fizikos terminų žodynas
Площадь поперечного сечения образца после разрыва Fк — Минимальная площадь поперечного сечения рабочей части образца после разрыва Источник: ГОСТ 1497 84: Металлы. Методы испытаний на растяжение оригинал документа … Словарь-справочник терминов нормативно-технической документации
Площадь поперечного сечения арматуры — Fa, мм2 – площадь поперечного сечения равновеликого по массе круглого гладкого образца, определяется по формуле где т – масса образца, г; l – длина образца, мм. [ГОСТ 10922 2012] Рубрика термина: Виды арматуры Рубрики… … Энциклопедия терминов, определений и пояснений строительных материалов
площадь поперечного сечения фильтра — Площадь фильтра перпендикулярная движению воды. [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN filter area … Справочник технического переводчика
площадь поперечного сечения арматуры — Аs — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы Аs EN cross sectional area of reinforcement … Справочник технического переводчика
площадь поперечного сечения бетона — Аc — [Англо русский словарь по проектированию строительных конструкций. МНТКС, Москва, 2011] Тематики строительные конструкции Синонимы Аc EN cross sectional area of concrete … Справочник технического переводчика
площадь поперечного сечения в месте разрушения — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN area of fracture … Справочник технического переводчика
площадь поперечного сечения вверх по потоку — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN upstream area … Справочник технического переводчика
площадь поперечного сечения вниз по потоку — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN downstream area … Справочник технического переводчика
