2. Закон Ома для участка и полной цепи
Закон Ома для участка цепи: сила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
Формула
закона: I=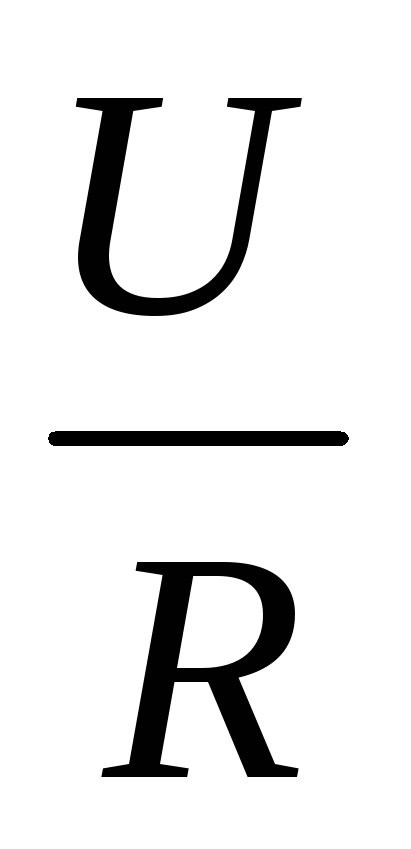 .
Отсюда запишем формулыU= IR и R
=
.
Отсюда запишем формулыU= IR и R
=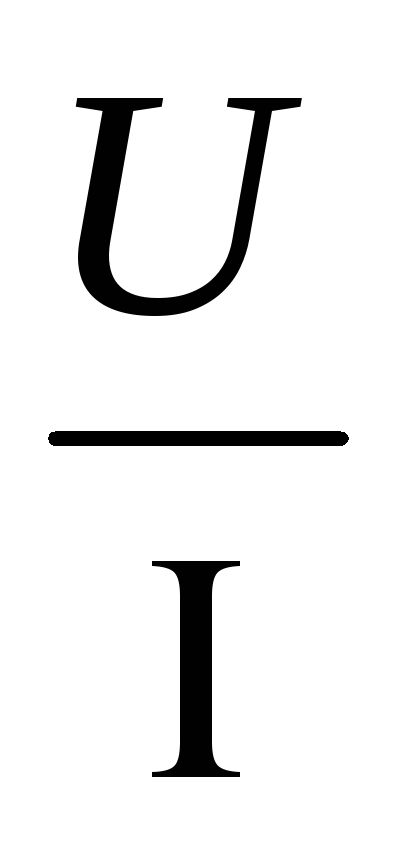 .
.
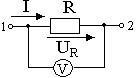 Рис.1.Участок
цепи
Рис.1.Участок
цепи 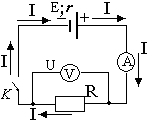
Закон
Ома для полной цепи: сила
тока I полной электрической цепи равна ЭДС
(электродвижущей силе) источника тока Е,
деленной на полное сопротивление цепи (R
+ r). Полное
сопротивление цепи равно сумме
сопротивлений внешней цепи R и внутреннего r источника тока. Формула
закона I
= 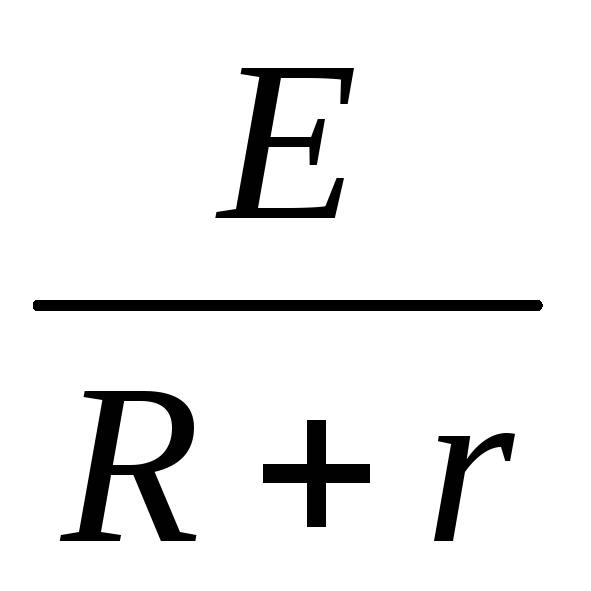 . На
рис. 1 и 2 приведены схемы электрических
цепей.
. На
рис. 1 и 2 приведены схемы электрических
цепей.
3. Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно. Смешанное соединение сочетает оба эти соединения.
Сопротивление, при включении которого вместо всех других проводников, находящихся между двумя точками цепи, ток и напряжение остаются неизменными,
называют эквивалентным сопротивлением этих проводников.Последовательное соединение
Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.
Как следует из первого правила Кирхгофа, при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).
1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I1 = I2 = I3 = I
Рис. 1. Последовательное соединение двух проводников.
2. Согласно закону Ома, напряжения U1 и U2 на проводниках равны U1 = IR1, U2 = IR2, U3 = IR3.
Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.
U = U1 + U2 + U3
По закону Ома, напряжения U1,U2на проводниках равны U1 = IR1, U2 = IR2, В соответствии вторым правилом Кирхгофа напряжение на всем участке:
U = U1 + U2 = IR1+ IR2 = I(R1+ R2)= I·R. Получаем: R = R1 + R2
Общее напряжение U на проводниках равно сумме напряжений U1, U2 ,U3 равно: U
где RЭКВ – эквивалентное сопротивление всей цепи. Отсюда: RЭКВ = R1 + R2 + R3
При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R ЭКВ= R1 +
R2 + R3+…Этот результат справедлив для любого числа последовательно соединенных проводников.
Из закона Ома следует: при равенстве сил тока при последовательном соединении:
I = 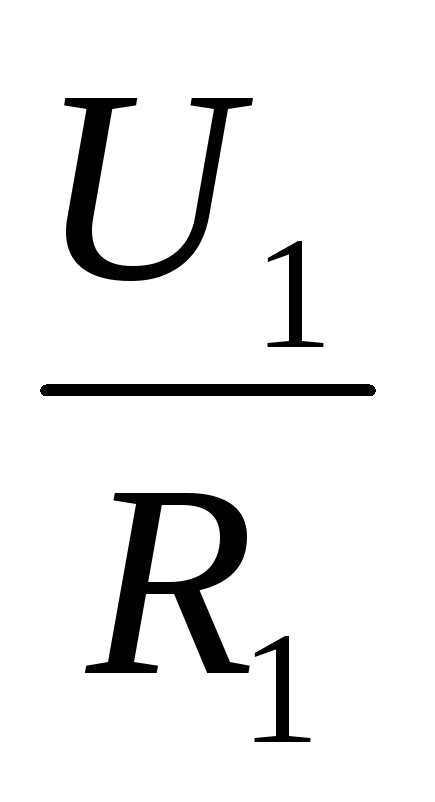 ,I =
,I = 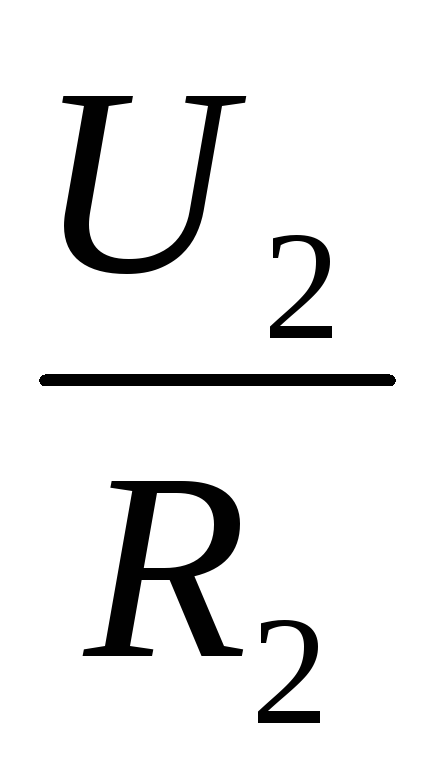 .
Отсюда
.
Отсюда  =
= 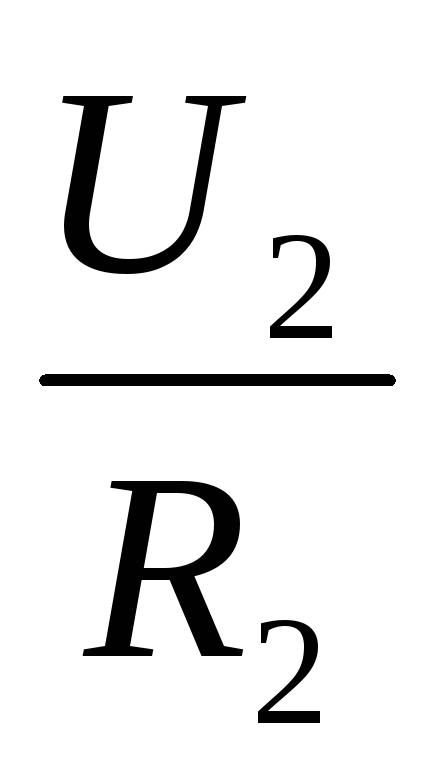 или
или 
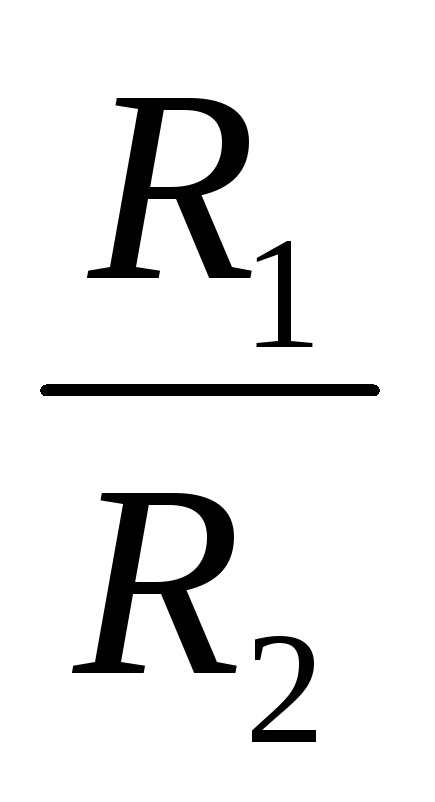 ,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.
,
т. е. напряжения на отдельных участках
цепи прямо пропорциональны сопротивлениям
участков.
При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U1 на их количество n:
UПОСЛЕД= n ·U1. Аналогично для сопротивлений: RПОСЛЕД = n· R1
При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.
studfile.net
для участка цепи, для полной цепи +ВИДЕО
Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга.
Содержание статьи
Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Разбираемся что такое ток и сопротивление
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.

Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.

Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Что изменится для полной цепи
В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.

Полная цепь включает в себя источник питания
Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).
Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:
Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.
Вроде не слишком сложно, но можно попробовать еще проще:
- Чем выше ЭДС источника тока, тем больше ток.
- Чем больше суммарное сопротивление, тем ток меньше.
Как найти сопротивление, напряжение
Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.

Формула напряжения и сопротивления по закону Ома
Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.
С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
elektroznatok.ru
Последовательное и параллельное соединение проводников
Проводники в электрических цепях могут соединяться последовательно и параллельно.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
I1 = I2 = I. | |
| |
Рисунок 1.9.1. Последовательное соединение проводников | |
По закону Ома, напряжения U1 и U2 на проводниках равны
U1 = IR1, U2 = IR2. |
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
U = U1 + U2 = I(R1 + R2) = IR, |
где R – электрическое сопротивление всей цепи. Отсюда следует:
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U1 и U2 на обоих проводниках одинаковы:
Сумма токов I1 + I2, протекающих по обоим проводникам, равна току в неразветвленной цепи:
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Например, к узлу A за время Δt подтекает заряд IΔt, а утекает от узла за то же время заряд I1Δt + I2Δt. Следовательно, I = I1 + I2.
|
Рисунок 1.9.2. Параллельное соединение проводников |
Записывая на основании закона Ома
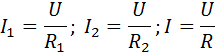
где R – электрическое сопротивление всей цепи, получим
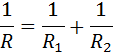
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
|
Рисунок 1.9.3. Расчет сопротивления сложной цепи. Сопротивления всех проводников указаны в омах (Ом) |
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
|
Рисунок 1.9.4. Пример электрической цепи, которая не сводится к комбинации последовательно и параллельно соединенных проводников |
Цепи, подобные изображенной на рис. 1.9.4, а также цепи с разветвлениями, содержащие несколько источников, рассчитываются с помощью правил Кирхгофа.
questions-physics.ru
Электрическая цепь с последовательным соединением элементов
|
|
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U1 + U2 + U3 или IRэкв = IR1 + IR2 + IR3,
откуда следует
Rэкв = R1 + R2 + R3.
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением Rэкв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
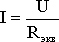 ,
,
и по вышеприведенным формулам рассчитывают падение напряжений U1, U2, U3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).

Рис. 1.6
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I1 + I2 + I3, т.е.
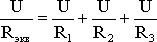
откуда следует, что
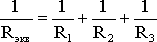 .
.
В том случае, когда параллельно включены два сопротивления R1 и R2, они заменяются одним эквивалентным сопротивлением
(1.7)
 .
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
gэкв = g1 + g2 + g3.
По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление Rэкв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IRэкв = I1R1 = I2R2 = I3R3.
Отсюда следует, что
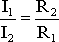 ,
,
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

Рис. 1.7
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R1=R2=R3=R4=R5=R. Сопротивления R4 и R5 включены параллельно, тогда сопротивление участка цепи cd равно:
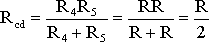 .
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
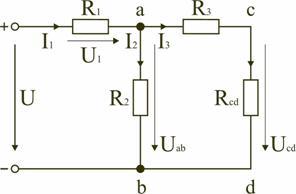
Рис. 1.8
На схеме (рис. 1.8) сопротивление R3 и Rcd соединены последовательно, и тогда сопротивление участка цепи ad равно:
 .
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
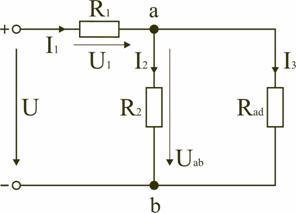
Рис. 1.9
На схеме (рис. 1.9) сопротивление R2 и Rad соединены параллельно, тогда сопротивление участка цепи аb равно
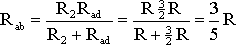 .
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R1 и Rab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
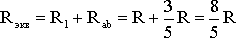 .
.
|
|
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением Rэкв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока
Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.
Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б).
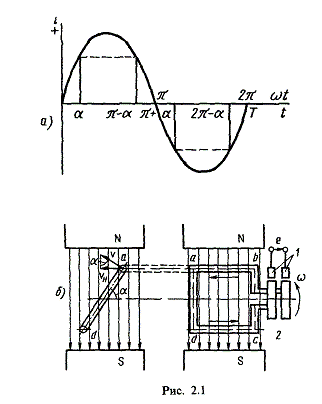
Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е. Нагрузку подключают к генератору с помощью щеток 1, прижимающихся к двум контактным кольцам 2, которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В, размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля vн:
e = Blvн (2.1)
где В и l — постоянные величины, a vн — переменная, зависящая от угла α. Выразив скорость vн через линейную скорость катушки v, получим
e = Blv·sinα (2.2)
В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α.
Если угол α = π/2, то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. Em = Blv. Поэтому выражение (2.2) можно записать в виде
e = Emsinα (2.3)
Так как α есть угол поворота за время t, то, выразив его через угловую скорость ω, можно записать α = ωt, a формулу (2.3) переписать в виде
e = Emsinωt (2.4)
где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.
Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е, напряжений и и токов i справедливы законы постоянного тока.
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е’.
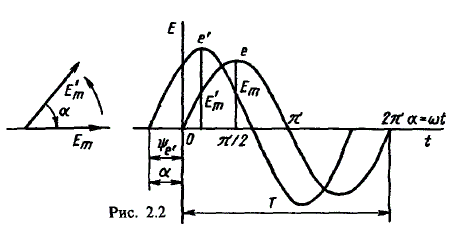
Если число пар полюсов магнитов p ≠ 1, то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,
f = Pn / 60
Из рис. 2.2 видно, что ωТ = 2π, откуда
ω = 2π / T = 2πf (2.5)
Величину ω, пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.
Графически изображенные на рис. 2.2 э. д. с. е и е’ можно описать выражениями
e = Emsinωt; e’ = E’msin(ωt + ψe’).
Здесь ωt и ωt + ψe’ — фазы, характеризующие значения э. д. с. e и e’ в заданный момент времени; ψe’ — начальная фаза, определяющая значение э. д. с. е’ при t = 0. Для э. д. с. е начальная фаза равна нулю (ψe = 0). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt), а отрицательную фазу — вправо.
Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.
Разность углов φ, равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α. Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).
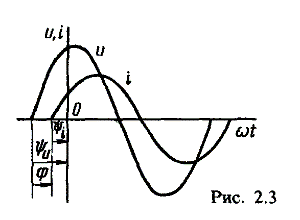
Когда для синусоидальных величин разность фаз равна ±π, то они противоположны по фазе, если же разность фаз равна ±π/2, то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.
Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:
u = Umsin(ωt + ψu); i = Imsin(ωt + ψi), (2.6)
причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψu — ψi.
Уравнения (2.6) можно записать иначе:
u = Umsin(ωt + ψi + φ); i = Imsin(ωt + ψu — φ),
поскольку ψu = ψi + φ и ψi = ψu — φ.
Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ).
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = Im·sin(ω·t + ψi), u = Um·sin(ω·t + ψu), e = Em·sin(ω·t + ψe),
где I, u, e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
Im, Um, Em – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψi, ψu, ψe – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.
Графики мгновенных значений тока и напряжения показаны на рис. 2.3
Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψu > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψi < 0. Алгебраическая величина, равная разности начальных фаз двух синусоид, называется сдвигом фаз φ. Сдвиг фаз между напряжением и током
φ = ψu – ψi = ψu – ( — ψi) = ψu + ψi.
Применение аналитической формы для расчёта цепей является громоздкой и неудобной.
На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением
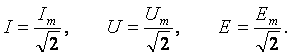
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
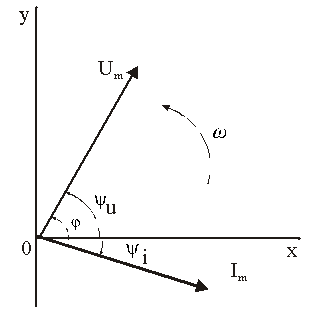 Рис.
2.4
Рис.
2.4
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4
3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
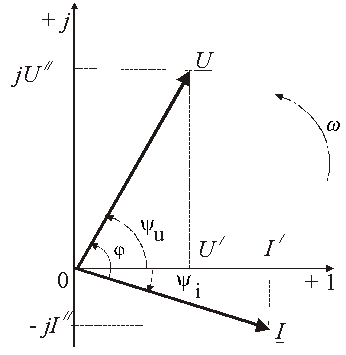 Рис.
2.5
Рис.
2.5
Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:
а). Алгебраической
U = U’+ jU«
I = I’ – jI«,
где U‘, U«, I‘, I» – проекции векторов на оси действительных и мнимых чисел.
б). Показательной
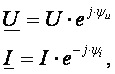
где U, I – модули (длины) векторов; е – основание натурального логарифма;  поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
поворотные
множители, т. к. умножение на них
соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
в). Тригонометрической
U = U·(cosψu + jsinψu)
I = I·(cosψi – jsinψi).
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
еj·ψ = cosψ + jsinψ.
Неразветвлённые электрические цепи
studfile.net
Параллельное соединение
Параллельным называется соединение проводников, при котором одни их концы образуют узел А, а другие – узел В.
 Узловые
точки (узлы)
– это точки, в которых сходятся не
менее трех проводников.
Узловые
точки (узлы)
– это точки, в которых сходятся не
менее трех проводников.
Параллельно соединенные проводники составляют разветвление, а каждая из них называется ветвью.
1. При параллельном соединении напряжения на всех ветвях и на всем разветвлении одинаковы, (как разности потенциалов двух точек А и В): U1=U2=U.
По первому правилу Кирхгофа (алгебраическая сумма токов, сходящихся в одном узле, равно нулю), имеем:
2. Сумма токов I1 + I2, протекающих по ветвям, равна силе тока I в неразветвленной части цепи: I = I1 + I2
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Следовательно, I = I1 + I2
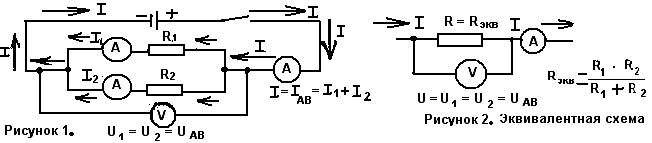
3. Токи
в отдельных ветвях разветвления обратно пропорциональны сопротивлениям этих
ветвей: 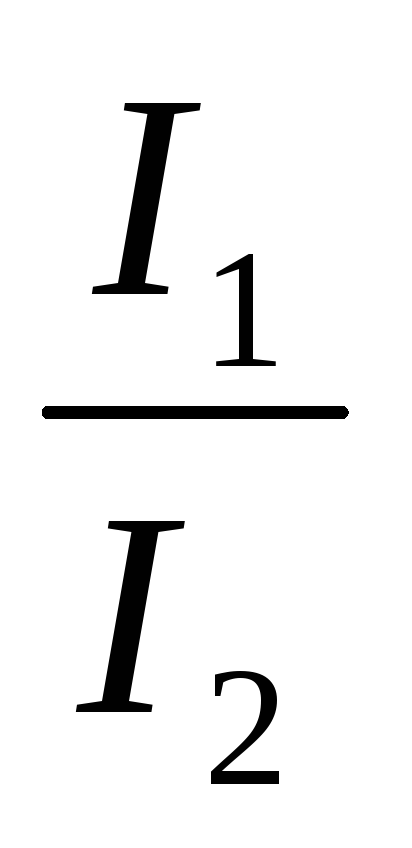 =
= 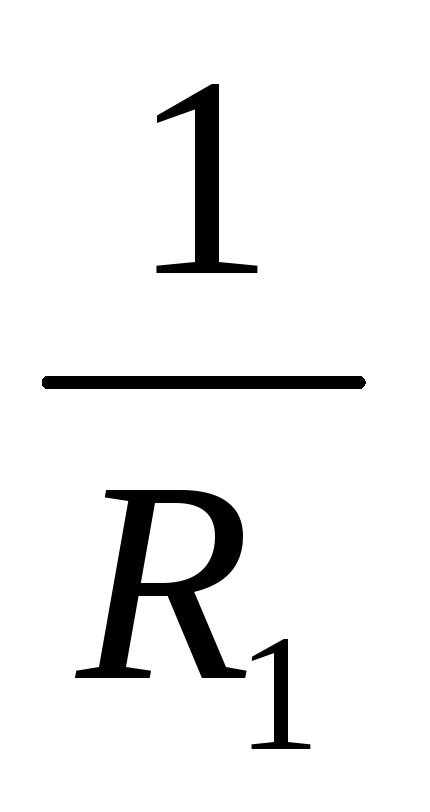 /
/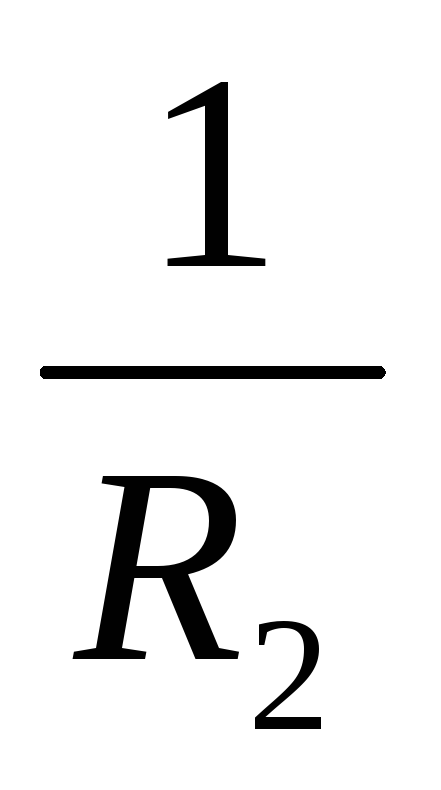
На
основании закона Ома: U1 = I1·R1, U2 = I2·R2 и учитывая,
что напряжения на ветвях одинаковы U1 = U2 = U, имеем: I1 R1 = I2 R2 или 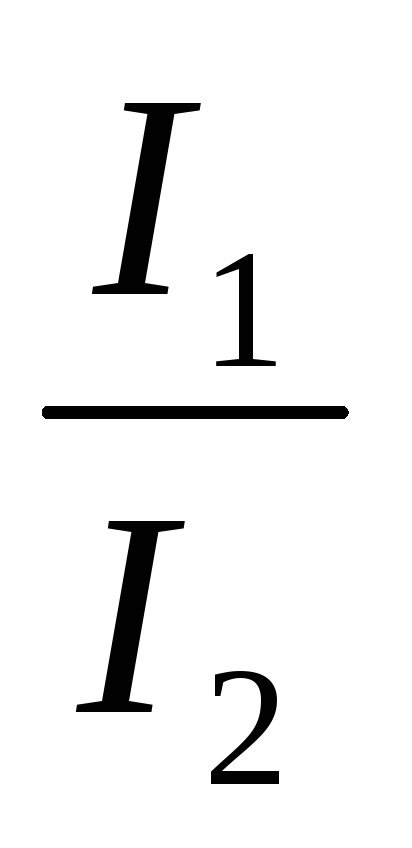 =
= 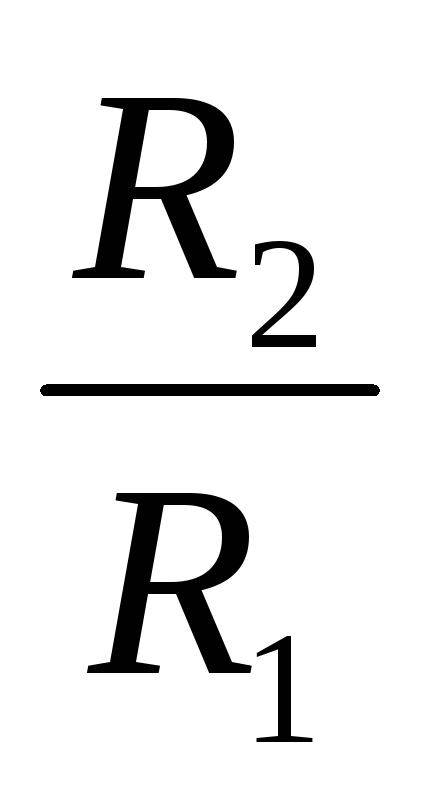 , т.
е.
, т.
е. 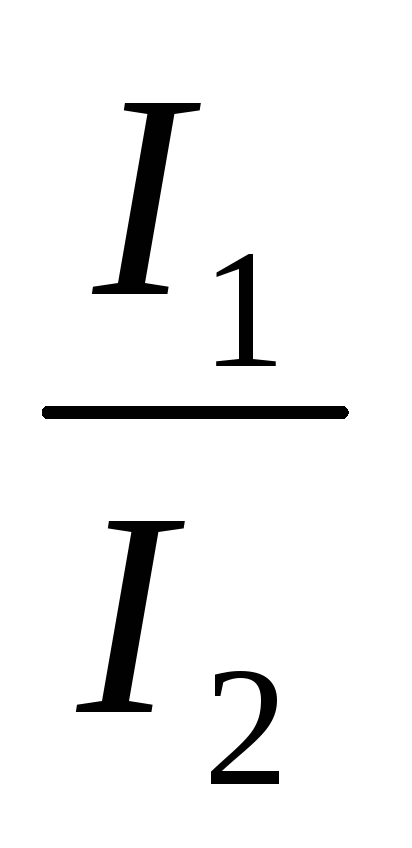 =
= 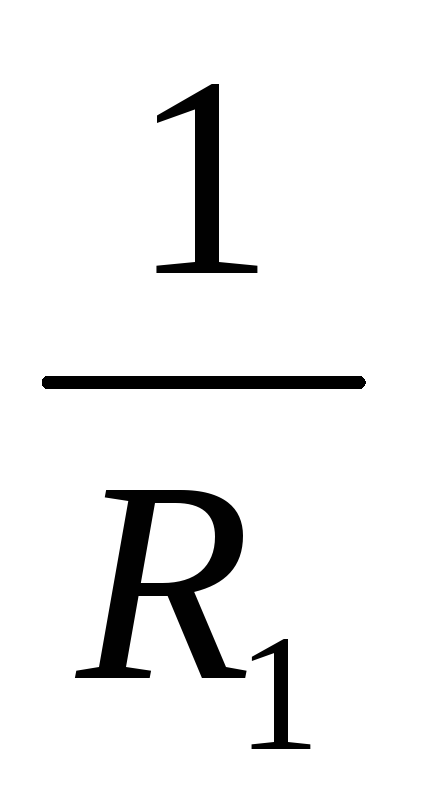 /
/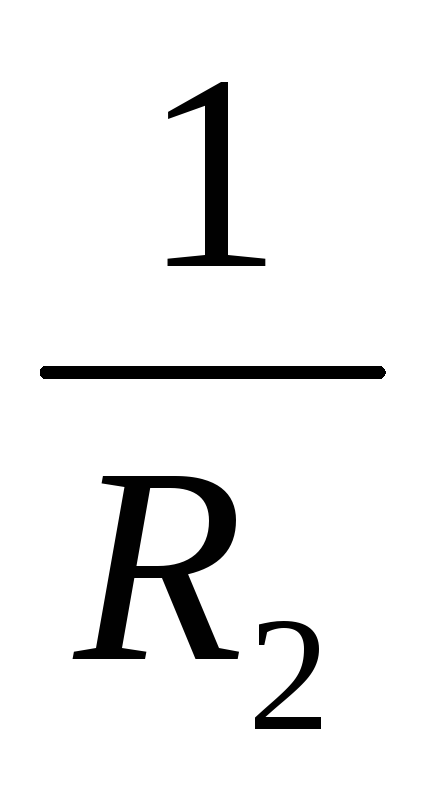
5. При параллельном соединении проводников величина, обратная эквивалентному (полному) сопротивлению участка цепи, равна сумме величин, обратных сопротивлению отдельных проводников.
Записывая
на основании закона Ома: 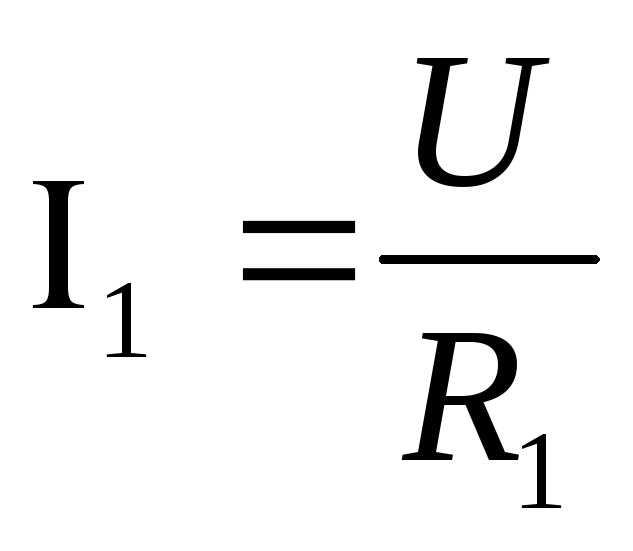 ,
,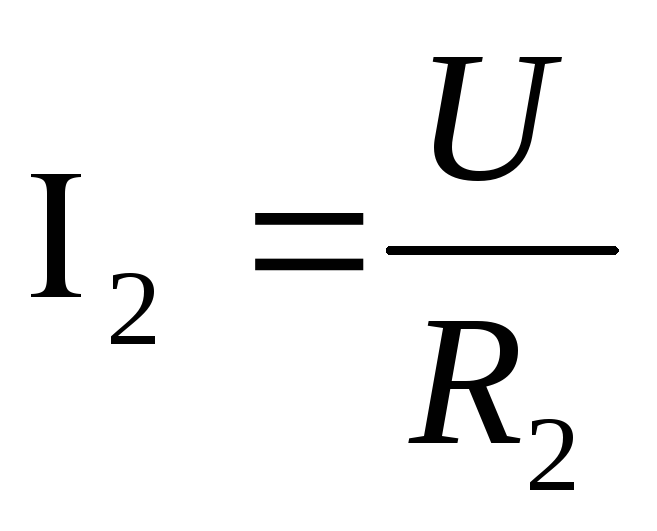 ,
,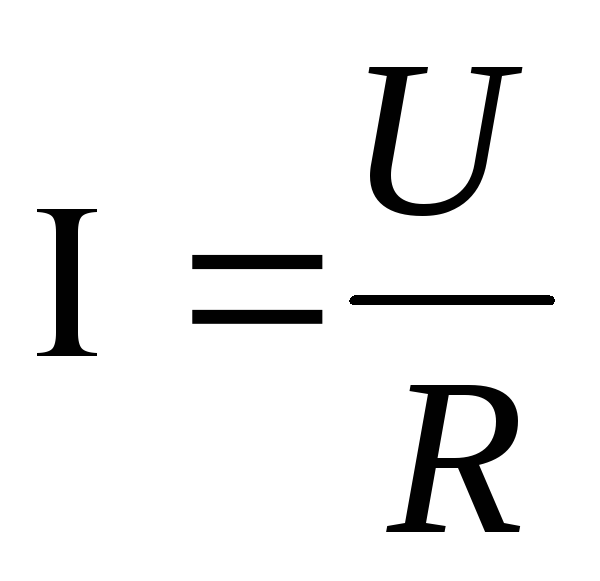 ,
где R – электрическое сопротивление всей
цепи (из двух ветвей), получим, учитывая,
что напряжения одинаковы на ветвях:
,
где R – электрическое сопротивление всей
цепи (из двух ветвей), получим, учитывая,
что напряжения одинаковы на ветвях: 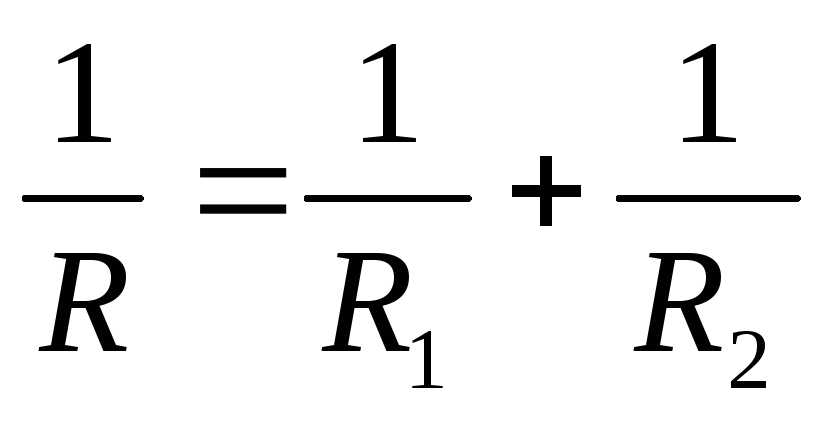 .
Для трех проводников:
.
Для трех проводников: 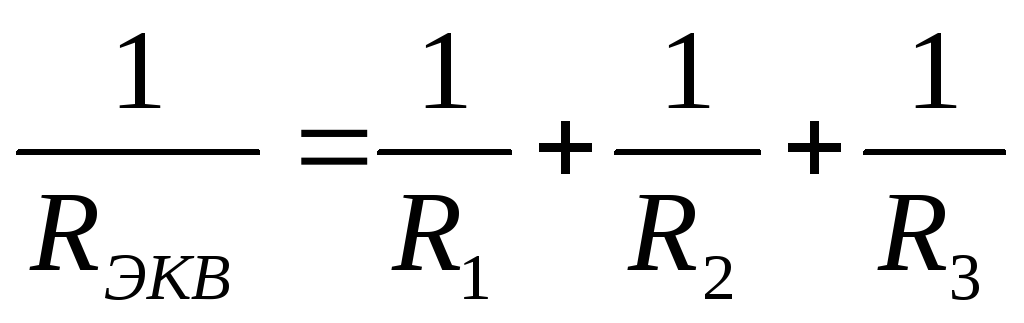 или: RЭКВ=
или: RЭКВ= 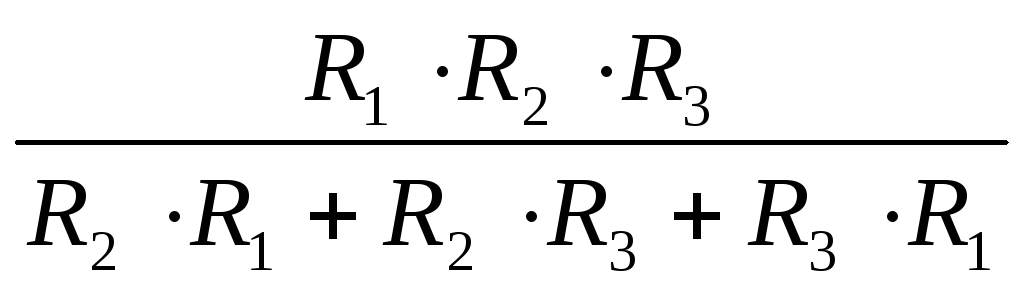
При
параллельном соединении двух проводников
формула упрощается: RЭКВ. =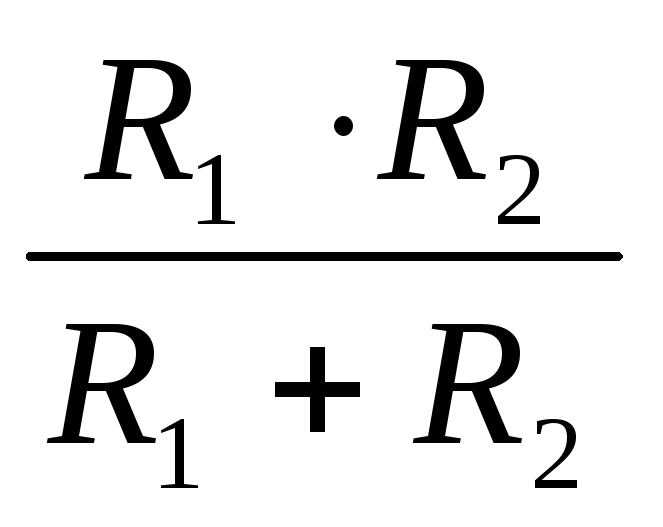
Этот результат справедлив для любого числа параллельно включенных проводников.
Величина,
обратная сопротивлению, называется проводимостью проводников: g = 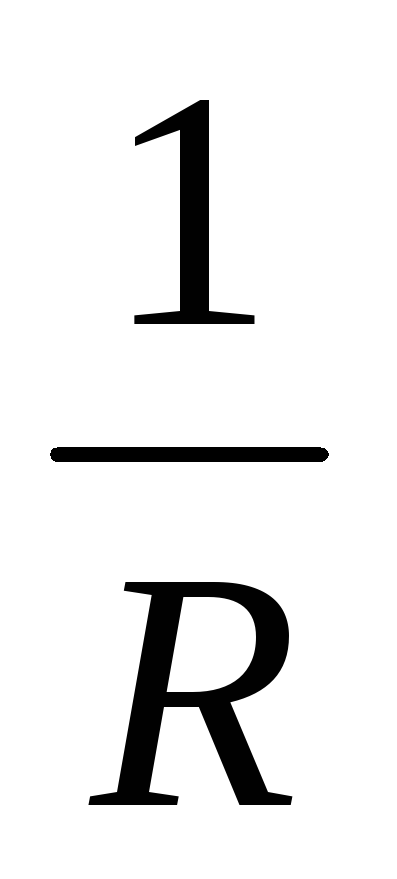 .
Тогда:gПАР= g1 + g2 + g3.
.
Тогда:gПАР= g1 + g2 + g3.
Единица проводимости – сименс, См. 1 См = 1 Ом -1. Сименс – электрическая проводимость проводника сопротивлением в 1 Ом.
Если
соединены параллельно n одинаковых проводников, то эквивалентное
сопротивление равно величине одного,
деленное на число ветвей разветвления n: RПАР = .
При параллельном соединении проводников эквивалентное
сопротивление меньше
наименьшего из сопротивлений. При этом общий ток
в цепи равен: IПАР= I1 ·n
.
При параллельном соединении проводников эквивалентное
сопротивление меньше
наименьшего из сопротивлений. При этом общий ток
в цепи равен: IПАР= I1 ·n
Если напряжение между узлами остается постоянным, то токи в ветвях не зависят друг от друга. Из этого следует, что на практике для потребителей удобнее пользоваться параллельным соединением.
4. Расширение пределов измерения амперметра и вольтметра
Задача. Предел измерения амперметра Iа = 2А. Каким образом можно измерить силу тока I = 10 А, если внутреннее сопротивление амперметра равен Rа = 0,4 Ом?
Решение. А) Для расширения предела измерения параллельно к амперметру присоединяют шунт сопротивлением Rш, через который будет проходить ток, равный Iш = I – Iа. Напряжение на шунте и амперметре будут одинаковы и равны U = Iа ·Rа = Iш·Rш
Отсюда
получаем: Rш =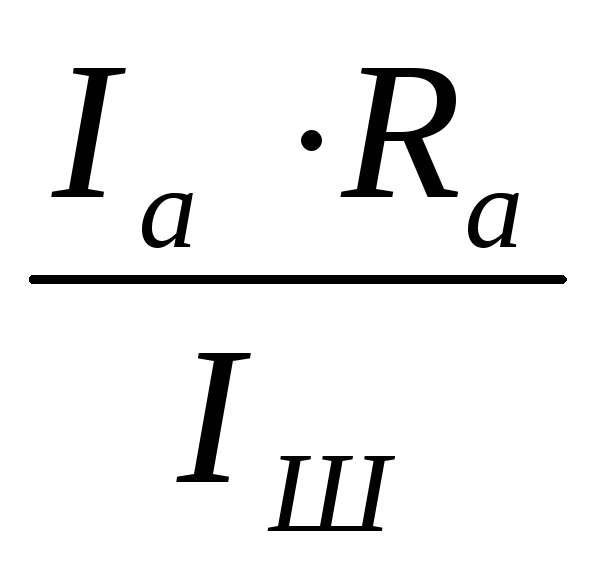 ; Rш=
; Rш=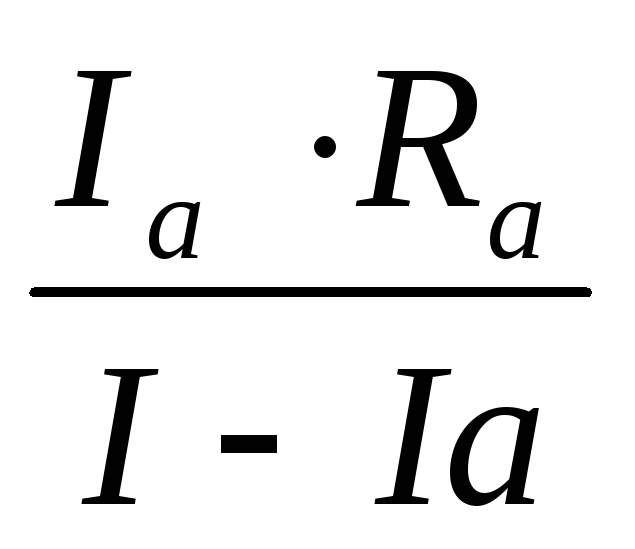 Разделим числитель и знаменатель наIа,
обозначим n =
Разделим числитель и знаменатель наIа,
обозначим n = 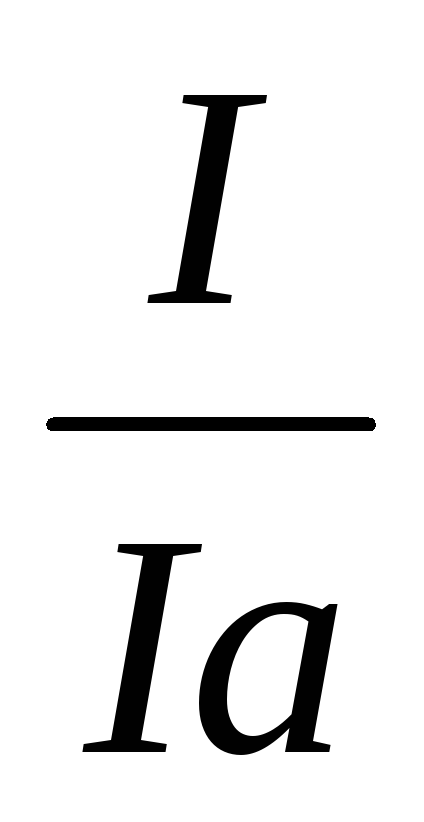 ,
тогда получим: Rш
=
,
тогда получим: Rш
= 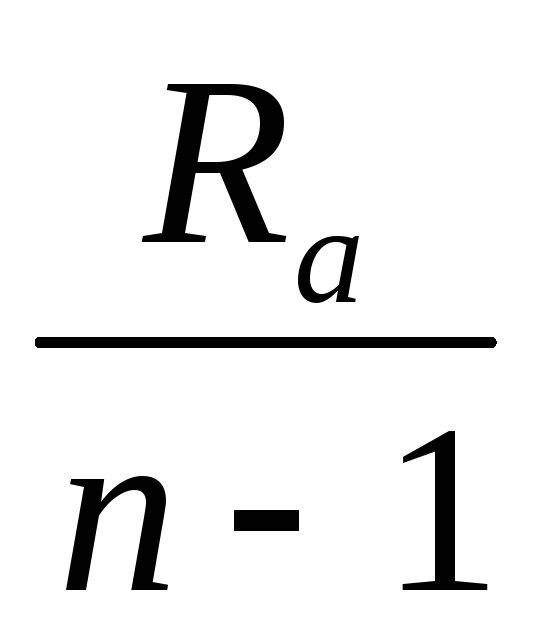
Подставив
числовые значения, получаем Rш= 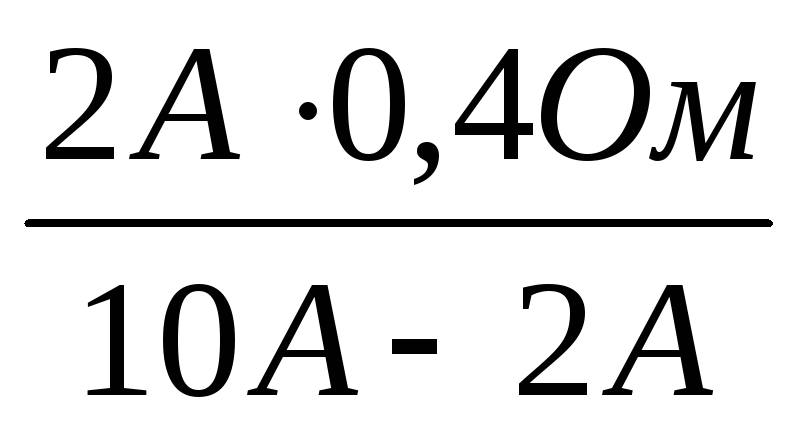 = 0,1 Ом
= 0,1 Ом
В) Или решаем по готовой формуле Rш=  ,
где n =
,
где n = 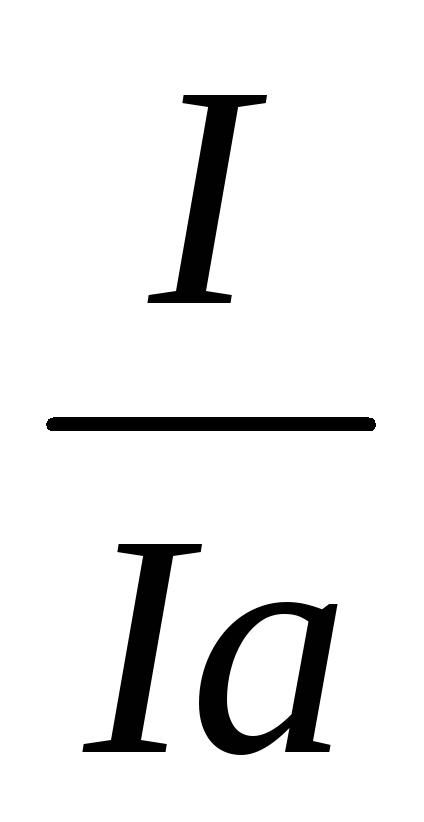 .
Вычислим: n =
.
Вычислим: n = 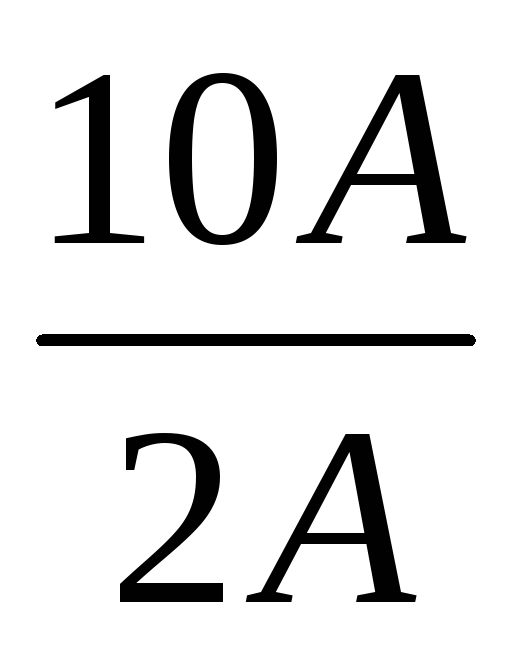 =
5; Rш
=
=
5; Rш
=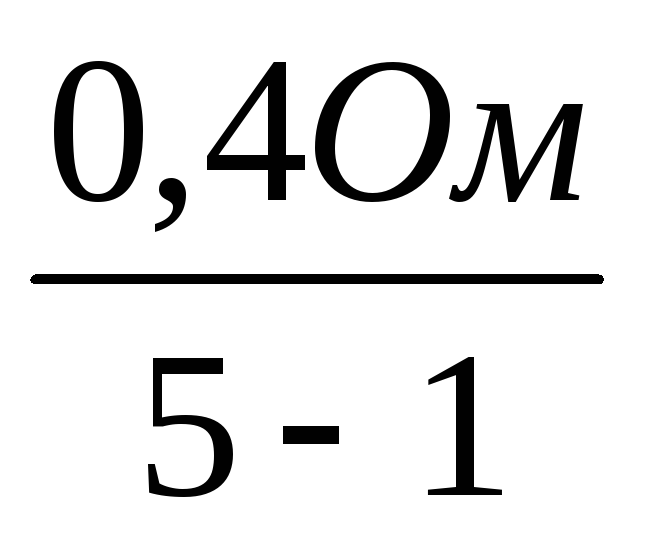 ==
0,1 Ом
==
0,1 Ом
Ответ. Параллельно к амперметру присоединить шунт сопротивлением RШ= 0,1Ом

Задача. А) Сопротивление вольтметра Rв=400 Ом, предел измерения Uв= 6В. Что необходимо сделать, чтобы данным вольтметром можно было измерить напряжение до U = 42 В?
Решение. А) Для расширения предела измерений к вольтметру присоединяют дополнительное сопротивление Uд = U – Uв
Сила тока, проходящего через вольтметр и дополнительное сопротивление, одинакова. Из закона Ома для участка цепи имеем:
I =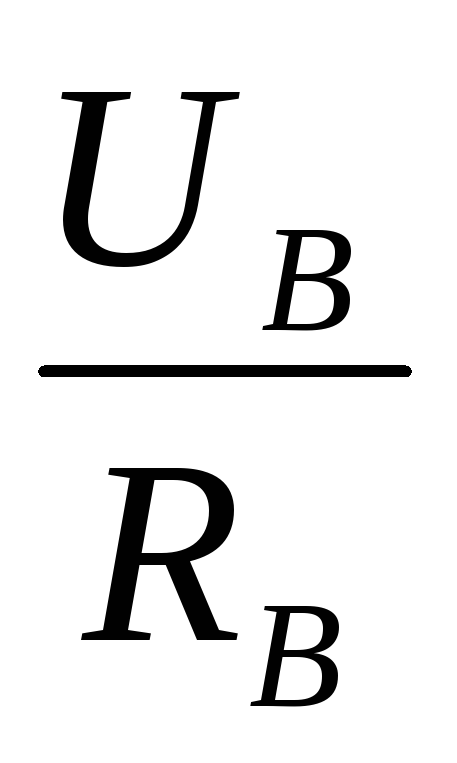 ; I =
; I = 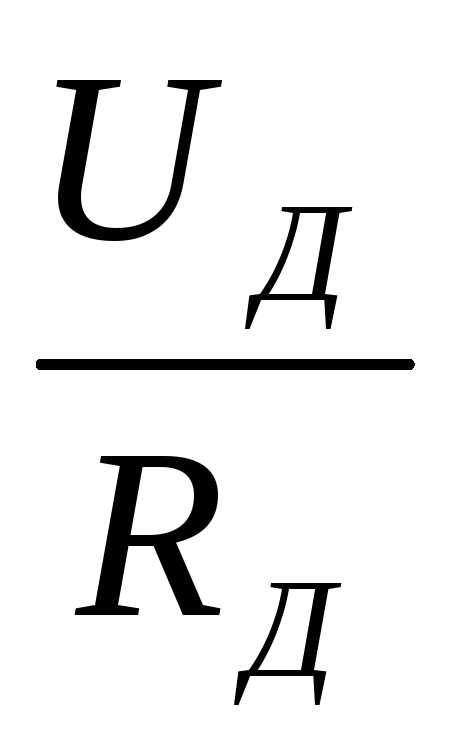 = I =
= I = 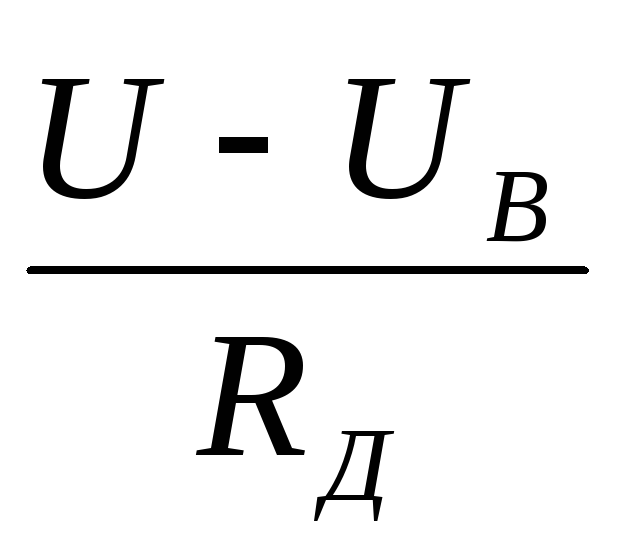 Отсюда:
Отсюда: 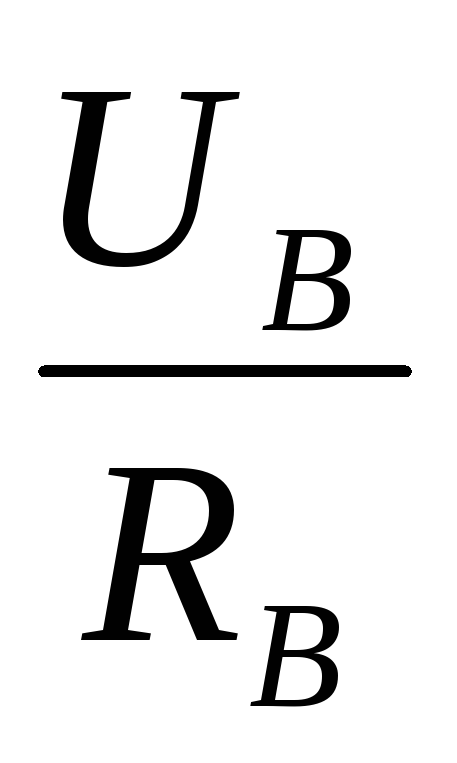 =
=  и Rд=
и Rд=
Разделим на Uв
числитель и знаменатель. Обозначим n =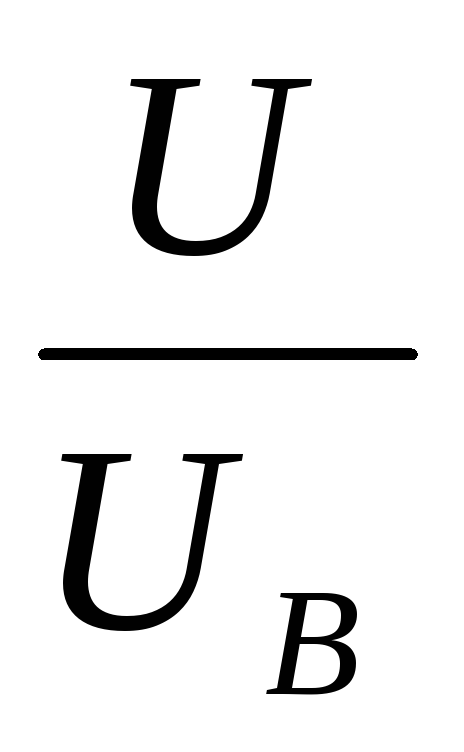 .
Тогда
получим: Rд
=Rв · (n – 1) Rд =
.
Тогда
получим: Rд
=Rв · (n – 1) Rд = 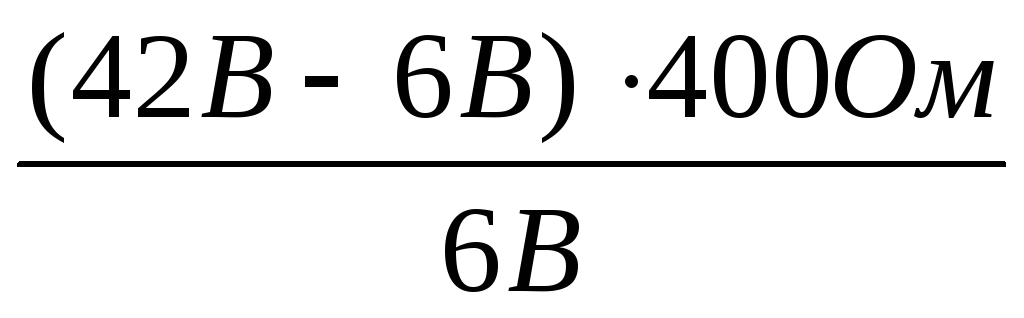 = 2400 Ом
= 2400 Ом
В) Или по формуле:
Rд
= Rв
· (n
– 1), где n
= 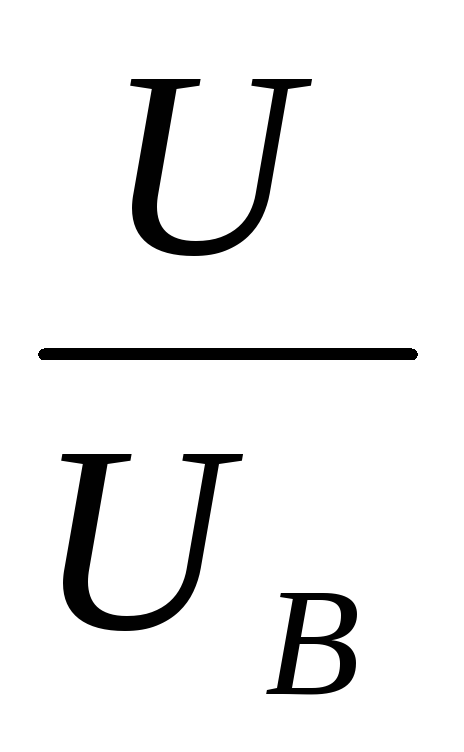 .
Вычислим:
n
=
.
Вычислим:
n
=  =
7;Rд
= 400 В ·(7– 1) = 2400 Ом; Rд =
2400 Ом
=
7;Rд
= 400 В ·(7– 1) = 2400 Ом; Rд =
2400 Ом
Ответ. Последовательно с вольтметром надо присоединить (добавку) резистор с сопротивлением RД = 2400 Ом
studfile.net
ФИЗИКА: ЗАДАЧИ на Параллельное соединение
Задачи на Параллельное соединение
проводников с решениями
Формулы, используемые на уроках «Задачи на Параллельное соединение проводников»
Название величины | Обозначение | Единица измерения | Формула |
Сила тока | I | А | I = U / R |
Напряжение | U | В | U = IR |
Сопротивление | R | Ом | R = U / I |
Сила тока на участке цепи | I | A | I = I1 + I2 |
Напряжение на концах участка | U | B | U = U1 = U2 |
Сопротивление участка цепи | R | Ом |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Два проводника сопротивлением 200 Ом и 300 Ом соединены параллельно. Определить полное сопротивление участка цепи.

Задача № 2. Два резистора соединены параллельно. Сила тока в первом резисторе 0,5 А, во втором — 1 А. Сопротивление первого резистора 18 Ом. Определите силу тока на всем участке цепи и сопротивление второго резистора.

Задача № 3. Две лампы соединены параллельно. Напряжение на первой лампе 220 В, сила тока в ней 0,5 А. Сила тока в цепи 2 А. Определите силу тока во второй лампе и сопротивление каждой лампы.

Задача № 4. Определите показания амперметра и вольтметра, если по проводнику с сопротивлением R1 идёт ток силой 0,1 А. Сопротивлением амперметра и подводящих проводов пренебречь. Считать, что сопротивление вольтметра много больше сопротивлений рассматриваемых проводников.

Задача № 5. В цепи батареи параллельно включены три электрические лампы. Нарисуйте схему включения двух выключателей так, чтобы один управлял двумя лампами одновременно, а другой — одной третьей лампой.
Ответ: 
Задача № 6. Лампы и амперметр включены так, как показано на рисунке. Во сколько раз отличаются показания амперметра при разомкнутом и замкнутом ключе? Сопротивления ламп одинаковы. Напряжение поддерживается постоянным.


Задача № 7. Напряжение в сети 120 В. Сопротивление каждой из двух электрических ламп, включенных в эту сеть, равно 240 Ом. Определите силу тока в каждой лампе при последовательном и параллельном их включении.

Задача № 8. Две электрические лампы включены параллельно под напряжение 220 В. Определите силу тока в каждой лампе и в подводящей цепи, если сопротивление одной лампы 1000 Ом, а другой 488 Ом.

Задача № 9. В цепь включены две одинаковые лампы. При положении ползунка реостата в точке В амперметр А1 показывает силу тока 0,4 А. Что показывают амперметры А и А2 ? Изменятся ли показания амперметров при передвижении ползунка к точке А?


Задача № 10. ОГЭ В сеть напряжением U = 24 В подключили два последовательно соединённых резистора. При этом сила тока составила I1 = 0,6 А. Когда резисторы подключили параллельно, суммарная сила тока стала равной I2 = 3,2 А. Определить сопротивления резисторов.

Задача № 11. ЕГЭ Миллиамперметр, рассчитанный на измерение тока до IА = 25 мА, имеющий внутреннее сопротивление RA = 10 Ом, необходимо использовать как амперметр для измерения токов до I = 5 А. Какое сопротивление должен иметь шунт?

Краткая теория для решения Задачи на Параллельное соединение проводников.

Это конспект по теме «ЗАДАЧИ на Параллельное соединение проводников». Выберите дальнейшие действия:
uchitel.pro
Урок решения задач по теме «Закон Ома для участка цепи, последовательное и параллельное соединения»
Цель урока: Закрепить изученный материал путем решения задач.
Задачи:
Образовательные:
- Научить учащихся решать задачи на последовательное и параллельное соединение проводников;
- Углубить и расширить знания о данных видах соединения проводников;
- Научить определять силу тока, напряжение, сопротивление при последовательном и параллельном соедини проводников;
- Научить решать задачи на смешанное соединение проводников;
- Научить учащихся разбираться в схемах электрических цепей.
Воспитательные:
- Развить личные качества учащихся: аккуратность, внимание, усидчивость;
- Воспитывать культуру общения при работе в группах.
Развивающие:
- Продолжить развитие навыков решения задач на данную тему;
- Продолжить развитие умений анализировать условия задач и ответов, умений делать выводы, обобщения;
- Продолжить развитие памяти, творческих способностей.
План урока
| № | Этап | Время | Метод |
| Организационный момент | 2 мин | Словесный | |
| I | Актуализация знаний | 5 мин | Письменная работа в парах |
| II | Вводная часть | 2 мин | Слово учителя, опрос учащихся |
| III | Решение задач | 45-50 мин | Работа учителя, учащихся у доски |
| IV | Работа учащихся в группах | 20 мин | Групповой работы, устный, письменный |
| V | Итог урока | 1-2 мин | Словесный метод |
Оформление класса: Проектор с экраном, доска с мелом. Раздаточный материал.
Слайд 1 включен в начале урока. Урок начинается с физического диктанта.
I. Актуализация знаний.
На слайде физический диктант. (Слайд 2). Учащимся выдается таблица для заполнения.
1. Заполнить двенадцать ячеек таблицы на карточке:
| Ученый | Физическая величина | Формула | Единица измерения |
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| Выполнил ______________ Проверил __________ Оценка__________ | |||
2. После заполнения таблиц учащиеся меняют карточками с соседом по парте, проверяют вместе с учителем и выставляют оценку:
| Кол-во ошибок | 1 | 2-3 | 4-6 | 7 и более |
| Оценка | 5 | 4 | 3 | 2 |
II. Вводное слово.
Сегодня на уроке мы с вами будем решать задачи на закон Ома, на последовательное и параллельное соединение проводников. (Слайд 3).
Запишите тему урока. (Слайд 4).
Для этого вспомним формулы и законы, которые нам пригодятся при решении задач.
III. Решение задач.
(3 ученика выходят к доске и записывают: первый закон Ома и выражает и него напряжение и сопротивление; второй – формулы справедливые для последовательного соединения; третий – формулы справедливые для последовательного соединения).
Задача 1. Для начала решим устную задачу на запоминание закона Ома. (Слайд 5)
a) U = 20B,R=10Om,I-?
б) I=10A,R = 5Om, R-?
в) I = 5A,U=15B,R-?
Ответ: а) I = 2А; б) U= 50 Ом; в) R = 3 Ом.
Задача 2. (Решает учитель с использованием презентации) Слайд 6.
Рассчитать силу тока, проходящую по медному проводу длиной 100м, площадью поперечного сечения 0,5мм2, если к концам провода приложено напряжение 6,8B.
Дано:
I=100м
S=0,5мм2
U=6,8В
I-?
Решение:
Ответ: Сила тока равна 2А.
Вопросы: Что известно из условия задачи? Какую величину необходимо определить? По какому закону будем определять силу тока? Какие величины нам неизвестны для нахождения силы тока и как их найти? ( – берется из таблицы). Теперь найдем R и полученное значение подставим в формулу для нахождения силы тока. (Перевод S в м2 не нужно делать, т.к. в единицах измерения плотности тоже присутствуют тоже мм2)
Задача 3. (Решает у доски сильный ученик) Условия задачи Слайд 7.
В электрическую цепь включены последовательно резистор сопротивлением 5 Ом и две электрические лампы сопротивлением 500 Ом. Определите общее сопротивление проводника.
Дано:
RAB=5 Ом
RBC=500 Ом
RCD=500 Ом
RAD-?
Решение:
Ответ: Общее сопротивление проводника равно 1005 Ом.
Вопросы: Какие элементы цепи нам даны? Как найти общее сопротивление?
Задача 4. (Класс делится на 2 группы, каждая из которой решает задачу своим способом (одни находя силу тока используя закон Ома, вторые используя формулу параллельного соединения). Затем по одному представителю пишут решения на доске) Условия задачи Слайд 8.
Два резистора сопротивлением r 1 = 5 Ом и r2= 30 Ом включены, как показано на рисунке, к зажимам источника тока напряжением 6В. Найдите силу тока на всех участках цепи.
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех участках цепи равна 1,4 А.
Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? Как найти I0? Что для этого неизвестно? Как найти I 1 и I2?
Второй способ решения данной задачи:
Дано:
r1=5 Ом
r2=30 Ом
U=6B
I0-?
Решение:
Ответ: Сила тока на всех участках цепи равна 1,4А.
Вопросы: Какой тип соединения рассматривается в задаче? Что известно из условия? Какие величины необходимо найти? По какой формуле будем находить общий ток в цепи? Какая величина нам неизвестна при нахождении силы тока и как ее найти?
Задача 5. (Решает ученик, можно вызвать два ученика по очереди). Определите полное сопротивление цепи и токи в каждом проводнике, если проводники соединены так, как показано на рисунке, а r1=1 Ом, r2=2 Ом, r3= 3 Ом, UAC = 11В. Условие задачи Слайд 9.
Дано:
r1=1 Ом
r2=2 Ом
r3=3 Ом
UAB=11B
RAC-?
I1-?
I2-?
I3-?
Решение:
Ответ: RАС =2,2 Ом, I1=2A, I2=3 А, I3=2A.
Вопросы: Какие типы соединения изображены на рисунке? Что нужно определить? Как найти полное сопротивление и величины в него входящие? Как найти силу тока в цепи? Как определить I1 и 12? Как определить UBC?
Задача 6. Условия задачи Слайд 10. (Вопросы 1,2,5 решаются устно. 3,4 – два ученика).
- Какому значению силы тока и напряжения соответствует точка А?
- Какому значению силы тока и напряжения соответствует точка В?
- Найдите сопротивление в точке А и в точке В.
- Найдите по графику силу тока в проводнике при напряжении 8 В и вычислите сопротивление в этом случае.
- Какой вывод можно проделать по результатам задачи?
Ответ:
- Сила тока = 0,4 А, напряжение – 4В.
- Сила тока = 0,6 А, напряжение – 6В.
- Сопротивление в т.А – 10 Ом, в т.В – 10 Ом.
- Сила тока = 0,8А, сопротивление – 10 Ом.
- При изменении силы тока и напряжения на одинаковую величину, сопротивление остается постоянным.
IV. Самостоятельная работа в группах.
Учащиеся делятся на 4 группы и каждой группе дается карточка с заданием.
Учитель объясняет критерии выставления оценок:
Во время работы в группах ведется наблюдение за более и менее активными участниками группы. Соответственно это будет влиять на более или менее высокую оценку при проверке записей в тетради, также будет учитываться уровень сложности решенных задач. Тетради с записями сдаются в конце урока. Время для решения задач ограниченное.
Задание 1. Слайд 11. (8 мин.)
Вопросы к карточкам:
- Перечислите все элементы цепи.
- Какие виды соединения используются?
- Рассчитайте напряжение на лампе.
- Рассчитайте напряжение на реостате.
- Рассчитайте силу тока на всем участке цепи.
Задание 2. Слайд 12. (4 мин.)
Определить общее сопротивление в цепи.
R1 = 2 Ом, R2 = 102 Ом, R 3 = 15 Ом, R4 = 4 Ом.
Задание 3. Слайд 13. (3 мин.)
Определите силу тока I при заданных U и R.
| Группа | R, Ом | U, В | I, А |
| I | 2 | 55 | ? |
| II | 14,2 | 87,4 | ? |
| III | 21 | 100 | ? |
| IV | 0,16 | 0,28 | ? |
Задание 4. Слайд 14. (5 мин)
Моток проволоки имеет сопротивление R и длину l .
Вычислить площадь поперечного сечения S.
| Группа | Материал | Параметры | ||
| Сопротивление | Длина проводника | Удельное сопротивление | ||
| R, Ом | l, мм2 | p, Ом·мм2/м | ||
| I | Медь | 0,83 | 33,9 | 1,7·10-2 |
| II | Алюминий | 16,1 | 83,1 | 2,8·10-2 |
| III | Серебро | 0,39 | 0,234 | 1,6·10-2 |
| IV | Сталь | 23,2 | 3,06 | 12·10-2 |
После выполнения заданий группами, тетради сдаются учителю.
V. Итог урока.
На сегодня все. Мы с вами научились решать задачи на последовательное и параллельное соединение проводников, закрепили знания о законе Ома для участка цепи.
Домашнее задание. Повторить все формулы и физические величины.
urok.1sept.ru

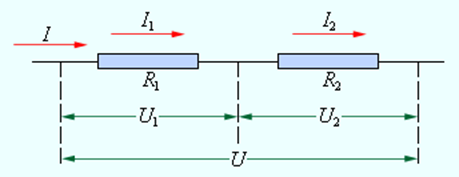
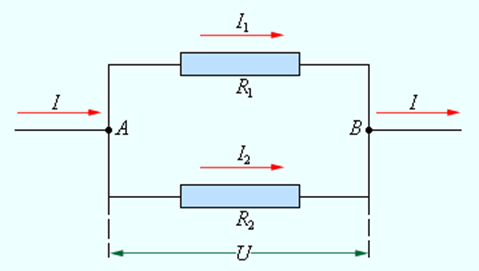
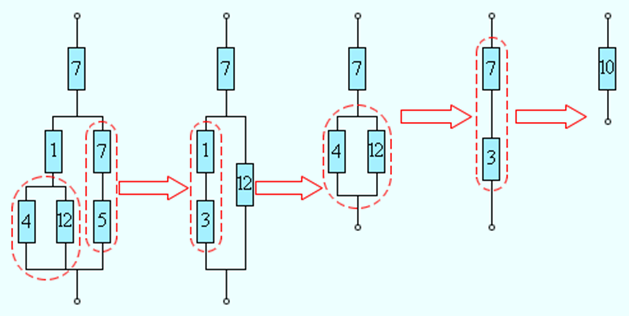
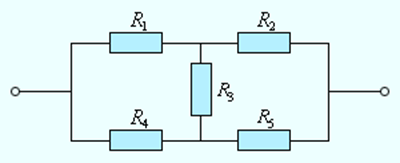
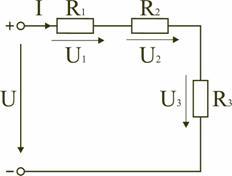 Рис.
1.4
Рис.
1.4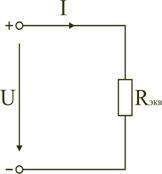 Рис.
1.5
Рис.
1.5 Рис.
1.10
Рис.
1.10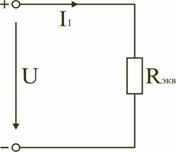 Рис.
1.11
Рис.
1.11