Селективный автоматический выключатель — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 декабря 2013; проверки требуют 7 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 17 декабря 2013; проверки требуют 7 правок. Селективный автоматический выключатель АББ S753DR E63, трехполюсной, 63 А

Селективный автоматический выключатель (англ. Selective Main Circuit Breaker) — это автоматический выключатель, имеющий в соответствии с немецким стандартом DIN VDE 0641-21 особую функцию селективности и исполняющий её независимо от напряжения сети. Это означает, что автомат не требует дополнительного питания для размыкания, замыкания контактов и для выполнения защитной функции (то есть устройство является чисто электро-механическим). Селективный автоматический выключатель полностью селективен нижестоящим модульным (миниатюрным) автоматическим выключателям.

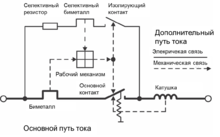Схема внутреннего устройства селективного автоматического выключателя

Появление селективного автоматического выключателя изначально планировалось, как выпуск устройства защиты, имеющего наилучшие характеристики с точки зрения выполнения функций вводного устройства защиты. Выше было отмечено, что это подразумевает обеспечение полной селективности. Это означает селективность между вводным и отходящими автоматическими выключателями во всём диапазоне токов короткого замыкания (вплоть до отключающей способности нижестоящего автомата) и при любых номинальных токах вводного автомата не меньше номинальных токов отходящего.

Такая функциональность обеспечивается конструкцией селективного автоматического выключателя (приведена на рисунке). На схеме видны два токовых пути. Один из них основной, имеющий те же элементы, что и обычный автоматический выключатель: электромагнитную катушку (мгновенный расцепитель), биметалл (расцепитель перегрузки) и блок основных контактов. Дополнительный токовый путь также имеет контакты. Помимо этого можно отметить наличие селективного биметалла. Рассмотрим процессы, происходящие внутри селективного автоматического выключателя в случае аварии.

Представим систему, в которой в качестве вводного устройства защиты используется селективный автоматический выключатель, а в качестве нижестоящего устройства защиты — миниатюрный автоматический выключатель. Возможны два случая. Первый — авария (короткое замыкание) происходит в нагрузке (за отходящим автоматом). Второй — авария происходит между вводным и отходящим автоматами.

В первом случае в момент короткого замыкания отработают расцепители миниатюрного автоматического выключателя и основного токового пути селективного автоматического выключателя. Однако, при этом ток продолжит протекать в дополнительном токовом пути вводного автомата. Поскольку авария устранена, пружина снова замкнет блок основных контактов. Таким образом обеспечивается непрерывное протекание тока и бесперебойность питания нагрузок, то есть селективность.

Во втором случае в момент аварии также разомкнутся основные контакты селективного автоматического выключателя. Далее, поскольку авария продолжит существовать, селективный биметалл также разомкнет контакты и дополнительном токовом пути, при этом заблокировав пружину и не позволив ей замкнуть основные контакты. Таким образом, разомкнутыми остаются и основной, и дополнительный токовый пути, тем самым обеспечивая защиту от короткого замыкания.

В итоге можно отметить, что селективный автоматический выключатель и обеспечивает селективность, и защищает от токов короткого замыкания.

Селективные автоматические выключатели предлагаются рядом немецких производителей. Из крупнейших брендов можно выделить ABB с их серией S750DR. Линейка Включает в себя автоматы от 0,5 до 63 А, существуют исполнения с характеристиками срабатывания Е и К.

Для применения на территории Российской Федерации селективные автоматические выключатели должны соответствовать нижеприведенным стандартам.

DIN VDE 0641-21[править | править код]

Основной стандарт, описывающий селективные автоматические выключатели. Появился в Германии в 2005 году. В данном нормативном документе приведены основные требованиям к параметрам, технические данные и описания испытаний.

ГОСТ Р 50030.2-2010[править | править код]

Аналог МЭК 60947-2-2006. Предъявляет общие требования к низковольтным (до 1000 В) автоматическим выключателям.

• DIN VDE 0641-21
• ГОСТ Р 50030.2-2010

Обсуждение:Автоматический выключатель — Википедия

Материал из Википедии — свободной энциклопедии

А как выбрать- сколькиполюсной выключатель нужен? 78.138.138.132 12:48, 7 мая 2010 (UTC)

«Минимальный ток, при котором должен срабатывать тепловой расцепитель, составляет 1,45 от номинального тока предохранителя.» — Почему??? Например, если сделать ток 1.2*Iном то автоматический выключатель сработает, но через более длительный промежуток времени!

1,45 от номинального тока — это ток, при котором автомат гарантированно сработает. При меньшем токе автомат может вообще не срабатывать, и это будет нормально (ГОСТ Р 50345-99, раздел 8.6.1.). —Кae 10:37, 20 января 2010 (UTC)

Коэффициент отключения[править код]

А почему в РФ 4500 считается нормой? В таком случае надо увеличивать толщину кабеля (к примеру, на 1,5 мм² меди тогда уже будет ограничение 13А, а для плиты уже 2,5 мм² меди не обойдёшься). В ЕС нижняя планка уже давно поднята до 6000, а нормой считается 10000, у вас же средства защитного отключения сами могут явится причиной пожара… Dmitry G 13:12, 30 июня 2008 (UTC)

• No comment 🙂 Chabrez 09:34, 25 июня 2010 (UTC)
  • к примеру, на 1,5 мм² меди тогда уже будет ограничение 13А, а для плиты уже 2,5 мм² меди не обойдёшься И таки да, вы правы! На 1,5 квадрата меди автомат нужно выбирать ещё меньше — 6 или 10 ампер. И для варочной поверхности таки да, нужен кабель с сечением 6 квадратов меди. Ваш Кэп Очевидность. —Зимин Василий 17:41, 22 ноября 2015 (UTC)

Эта статья неполная и описывает в основном модульные (бытовые) выключатели. Мало упомянуто о промышленных автоматических выключателях по ГОСТ Р 50030.2, хоть и есть ссылка на устаревший ГОСТ9098. — Sykorsky 08:35, 23 июня 2010 (UTC)

Если вы владеете информацией, то пишите! —Кae 09:12, 23 июня 2010 (UTC)

Авгиевы конюшни. Необходимо привести терминологию в соответствие с ГОСТ 17703—72. Чернышев Д. В. 11:03, 22 мая 2012 (UTC)

Здесь просто секция про модульные автоматы, это даже не статья. И даже черновой вариант к этой статье сложно сделать, дабы придётся из каждой секции выдирать по предложению. Будем стараться, главное чтобы администраторы отнеслись с пониманием. 90.191.190.76 10:58, 15 декабря 2012 (UTC)

Максимально поправил, но вообще статью надо разбить на низкое напряжение, среднее напряжение и высокое напряжение; пока что ещё статья написана про модульные автоматы низкого напряжения. Просто надо дня на два засесть за написание статьи, а у меня такого большого количества времени нет, да и после работы голова не так хорошо варит. 90.191.190.76 12:45, 16 декабря 2012 (UTC)

Закоментировал раздел селективность так как в данном виде это ОРИСС в чистом виде. Информация в разделе ошибочна и нуждается в куче уточнений и дополнений. В данном виде использовать нельзя. Но возможно имеет смысл оставить как заготовку.188.168.92.212 06:08, 29 апреля 2013 (UTC)

Перенесено из статьи:

В отличие от плавких предохранителей, автомат защиты линии имеет более сложную селективность. Это связано с наличием магнитного расцепителя. Селективности можно достичь следующими способами:

Сторона питания	Сторона потребителя	Описание
Плавкий предохранитель	Автомат	В таком случае время срабатывания плавкого предохранителя больше, чем у автомата, соответственно быстрее сработает автомат защиты.[источник не указан 2512 дней]
Автомат с характеристикой E	Автомат с характеристикой B, C или D	В таком случае время срабатывания автомата с характеристикой E больше, чем у автомата с характеристикой B, C или D, соответственно быстрее сработает автомат защиты с характеристикой B, C или D.
Автомат с характеристикой K	Автомат с характеристикой B или C	В таком случае время срабатывания автомата с характеристикой K больше, чем у автомата с характеристикой B или C, соответственно быстрее сработает автомат защиты с характеристикой B или C.
Автомат с характеристикой B, C или D	Автомат с характеристикой B, C или D	Селективность будет достигнута только в одном единственном случае: если ток короткого замыкания на стороне потребителя будет недостаточен для срабатывания магнитного расцепителя на стороне питания. На практике желаемый результат достигается крайне редко.
Автомат защиты	Плавкий предохранитель	Возможно только с автоматическими выключателями в литом корпусе, у которых имеется возможность настроить кривую отключения. При использовании модульных автоматов защиты, селективность достигнута не будет.

—MMH 23:59, 21 ноября 2015 (UTC)

Выключатели с зависимым включением[править код]

В некоторых стабилизаторах напряжения используются двухмодульные автоматические выключатели. Речь об СНВТ-3000\1 ( E — NEXT )Левый — «ШУНТ» правый — » СТАБИЛИЗАТОР » Возможные положения либо оба выключены, либо включен только один из них. Т. е. если у Вас включен » СТАБИЛИЗАТОР «, а Вы пытаетесь включить «ШУНТ»= включенный автомат » СТАБИЛИЗАТОР » немедленно отстреливается. Я бы сказал, что это мощный аналог проходного выключателя. По моему мнению такие автоматы следует класифицировать как

 " Двухмодульные  автоматические выключатели с зависимым включением "
82.207.35.20 12:46, 5 сентября 2016 (UTC)

В тексте «Устройство» указаны цифры в круглых скобочках. Так понимаю, что это из какого-то описания. Думаю эти цифры надо или удалить или добавить фотографию которой они соответствуют.— Estimata698 (обс.) 10:22, 25 ноября 2019 (UTC)

Автоматический выключатель постоянного тока — Википедия

Материал из Википедии — свободной энциклопедии

Быстродействующий выключатель ВАБ-49

Автоматические выключатели постоянного тока нужны чтобы отключать электрические цепи под нагрузкой. На тяговых подстанциях выключатели служат для отключения питающих линий в при перегрузках и токах короткого замыкания и для отключения обратного тока у выпрямителей при обратных зажиганиях или пробое вентилей. Гашение электрической дуги происходит на дугогасительных рогах или в дугогасительной камере. Удлинение дуги может быть выполнено при помощи магнитного дутья или в камерах с узкими щелями. Во всех случаях отключения цепи и возникновения электрической дуги происходит естественное движение дуги вверх вместе с движением нагретого воздуха, другими словами тепловое дутье.

Дугогасительная камера быстродействующего выключателя ВАБ-49

• Тяговые подстанции: учебник для вузов ж.-д. транспорта/ Бей Ю. М., Мамошин Р. Р. и др.-1986
• Руководство к лабораторным работам по дисциплине «Тяговые и трансформаторные подстанции»/ А. Н. Штин, Г. С. Кузнецова — Екатеринбург: Издательство УрГУПС, 1999
• Проектирование тяговых и трансформаторных подстанций: учебно-методическое пособие/ А. Н. Штин, Т. А. Несенюк — Екатеринбург: Издательство УрГУПС, 2014

Автоматический выключатель, управляемый дифференциальным током, со встроенной защитой от сверхтока

Материал из Википедии — свободной энциклопедии

Автоматический выключатель, управляемый дифференциальным током, со встроенной защитой от сверхтока (АВДТ) (residual current operated circuit-breaker with integral overcurrent protection, RCBO) или Дифференциальный автомат: Коммутационное устройство, управляемое дифференциальным током, предназначенное выполнять функции защиты от перегрузок и (или) коротких замыканий ^[1]. Изготавливают по стандарту IEC 61009-1. Residual current operated circuit-breakers with integral overcurrent protection for household and similar uses (RCBOs) – Part 1: General rules.

АВДТ с отключающим дифференциальным током IΔn 0,03 А

1. Состоит из двух электрически и механически связанных между собой частей:
   • двух- или четырёхполюсного автоматического выключателя с механизмом независимого расцепления и рейкой сброса внешним механическим усилием;
   • модуля защиты от поражения током МДЗ, обеспечивающим обнаружение дифференциального тока на землю, его преобразование, усиление и механическое воздействие на рейку сброса выключателя.
2. Электрический выключатель и МДЗ включены последовательно, чем обеспечивается питание электронного усилителя МДЗ и поддерживается его рабочий режим.
3. Для проверки функционирования дифавтомата в эксплуатации предусмотрена цепь контроля с кнопкой «Тест». (рис 2) Внутреннее устройство блока «МДЗ», от АД14, номинальный ток 32 А
4. МДЗ содержит датчик — дифференциальный трансформатор Д (рис 2, 1), осуществляющий обнаружение остаточного тока и расположенный на силовых проводах (рис 2, 2), электронный усилитель А (рис 2, 3), на выходе которого включена катушка электромагнитного сброса (рис 2, 4).
5. При установке рычага управления (рис 1, 4) подключенного к сети выключателя в положение «ВКЛ», получает питание усилитель А, вход которого подключен к информационной (вторичной) обмотке III датчика Д.
6. При протекании по силовым проводам МДЗ тока нагрузки, в магнитопроводе датчика (рис 2, 1) создаются равные, противоположно направленные магнитные потоки и в обмотке III практически не наводится напряжение. Выключатель остается во включенном положении.
7. При появлении дифференциального тока (в результате повреждения изоляции токоведущих частей или через тело прикоснувшегося человека), равенство потоков нарушается и в обмотке III наводится напряжение, примерно пропорциональное дифференциальному току. Это напряжение прикладывается ко входу усилителя А.
8. При определенном значении этого напряжения (уставка срабатывания), усилитель А открывается и подает ток от дополнительного источника питания на катушку К электромагнита сброса (рис 2, 4).
9. Электромагнит сброса сдергивает защелку механизма независимого расцепления (рис 2, 5) выключателя. Происходит принудительное размыкание его контактов. Тот же процесс имеет место при обрыве цепи обмотки III. Аналогично размыкаются контакты выключателя под воздействием защиты от сверхтоков и превышении напряжения сети максимального установленного значения.

1. ↑ ГОСТ IEC 60050-442—2015. Международный электротехнический словарь. Часть 442. Электрические аксессуары

Выключатели автоматические дифференциального тока со встроенной защитой от сверхтоков АВДТ32. Руководство по монтажу и эксплуатации. 3421-010-18461115-2008РЭ.

Выключатели автоматические дифференциального тока со встроенной защитой от сверхтоков АД12, АД14. Руководство по монтажу и эксплуатации. АГИЕ.641243.039РЭ.

Теория автоматов — Википедия

Материал из Википедии — свободной энциклопедии

Теория автоматов — раздел дискретной математики, изучающий абстрактные автоматы — вычислительные машины, представленные в виде математических моделей — и задачи, которые они могут решать.

Теория автоматов наиболее тесно связана с теорией алгоритмов: автомат преобразует дискретную информацию по шагам в дискретные моменты времени и формирует результат по шагам заданного алгоритма.

Символ — любой атомарный блок данных, который может производить эффект на машину. Чаще всего символ — это буква обычного языка, но может быть, к примеру, графическим элементом диаграммы.

• Слово — строка символов, создаваемая через конкатенацию (соединение).
• Алфавит — конечный набор различных символов (множество символов)
• Язык — множество слов, формируемых символами данного алфавита. Может быть конечным или бесконечным.

Автоматы

Автоматы могут быть детерминированные и недетерминированные.

Детерминированный конечный автомат (ДКА) — последовательность (кортеж) из пяти элементов (Q,Σ,δ,S0,F){\displaystyle (Q,\Sigma ,\delta ,S_{0},F)}, где:

Недетерминированный конечный автомат (НКА) — последовательность (кортеж) из пяти элементов (Q,Σ,Δ,S,F){\displaystyle (Q,\Sigma ,\Delta ,S,F)}, где:

• Q{\displaystyle Q} — множество состояний автомата
• Σ{\displaystyle \Sigma } — алфавит языка, который понимает автомат
• Δ{\displaystyle \Delta } — отношение перехода, Δ={<q,a,p>:q,p∈Q,a∈Σ∪{e}}{\displaystyle \Delta =\{<q,a,p>:q,p\in Q,a\in \Sigma \cup \{e\}\}}, где {e}{\displaystyle \{e\}} — пустое слово. То есть, НКА может совершить скачок из состояния q в состояние p, в отличие от ДКА, через пустое слово, а также перейти из q по a несколько состояний (что опять же в ДКА невозможно)
• S⊆Q{\displaystyle S\subseteq Q} — множество начальных состояний
• F⊆Q{\displaystyle F\subseteq Q} — множество конечных состояний.

Слово

Автомат читает конечную строку символов a₁,a₂,…., a_n , где a_i ∈ Σ, которая называется входным словом. Набор всех слов записывается как Σ*.

Принимаемое слово

Слово w ∈ Σ* принимается автоматом, если q_n ∈ F.

Говорят, что язык L читается (принимается) автоматом M, если он состоит из слов w на базе алфавита Σ{\displaystyle \Sigma } таких, что если эти слова вводятся в M, по окончанию обработки он приходит в одно из принимающих состояний F:

L={w∈Σ⋆|δ^(S0,w)∈F}{\displaystyle L=\{w\in \Sigma ^{\star }|{\hat {\delta }}(S_{0},w)\in F\}}

Обычно автомат переходит из состояния в состояние с помощью функции перехода δ{\displaystyle \delta }, читая при этом один символ из ввода. Есть автоматы, которые могут перейти в новое состояние без чтения символа. Функция перехода без чтения символа называется ϵ{\displaystyle \epsilon }-переход (эпсилон-переход).

Теория автоматов лежит в основе всех цифровых технологий и программного обеспечения, так, например, компьютер является частным случаем практической реализации конечного автомата.

Часть математического аппарата теории автоматов напрямую применяется при разработке лексических и синтаксических анализаторов для формальных языков, в том числе языков программирования, а также при построении компиляторов и разработке самих языков программирования, описания аппаратуры, а также разметки.

Другое важнейшее применение теории автоматов — математически строгое нахождение разрешимости и сложности задач.

Типовые задачи[править | править код]

• Построение и минимизация автоматов — построение абстрактного автомата из заданного класса, решающего заданную задачу (принимающего заданный язык), возможно, с последующей минимизацией по числу состояний или числу переходов.
• Синтез автоматов — построение системы из заданных «элементарных автоматов», эквивалентной заданному автомату. Такой автомат называется структурным. Применяется, например, при синтезе цифровых электрических схем на заданной элементной базе.

• Виктор Михайлович Глушков. Синтез цифровых автоматов. — М.: Государственное издательство физико-математической литературы, 1962. — С. 476.

• Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман. Введение в теорию автоматов, языков и вычислений = Introduction to Automata Theory, Languages, and Computation. — М.: Вильямс, 2002. — С. 528. — ISBN 0-201-44124-1.
• Касьянов В. Н. Лекции по теории формальных языков, автоматов и сложности вычислений. — Новосибирск: НГУ, 1995. — C. 112.

Автомат (механизм) — Википедия

Материал из Википедии — свободной энциклопедии

У этого термина существуют и другие значения, см. Автомат.

Автома́т — машина, самостоятельно действующее устройство (или совокупность устройств), выполняющее по жёстко заданной программе, без непосредственного участия человека, процессы получения, преобразования, передачи и использования энергии, материала и информации. Автоматы применяются для обеспечения комфортных условий жизни человека, повышения производительности, облегчения и обеспечения безопасности его труда.

Автоматы известны с древности, первые автоматы представляли собой движущиеся фигуры людей и животных.

Автоматические устройства XVIII—XIX веков основывались на принципах и методах классической механики. Развитие электротехники, практическое использование электричества в военном деле, связи и на транспорте привели к ряду открытий и изобретений, послуживших научной и технической базой для новых типов автоматов, действующих при помощи электричества. Важное значение имели работы русских учёных: изобретение П. Л. Шиллингом магнитоэлектрического реле (1830) — одного из основных элементов электроавтоматики, разработка Ф. М. Балюкевичем, В. М. Тагайчиковым и др. в 80-х годах XIX века ряда устройств автоматической сигнализации на железнодорожном транспорте, создание С. М. Апостоловым-Бердичевским совместно с М. Ф. Фрейденбергом первой в мире автоматической телефонной станции (1893—1895), и многие другие.

Начало промышленного использования автоматов относится к периоду промышленной революции XVIII века. К автоматическим устройствам этого времени, имевшим в основном экспериментальный характер, относятся: в России — автоматический суппорт Андрея Нартова для токарно-копировальных станков (1820-е годы), поплавковый регулятор уровня воды в котле И. И. Ползунова (1765), в Англии — центробежный регулятор Дж. Уатта (1784), во Франции — ткацкий станок с программным управлением от перфокарт для выработки крупноузорчатых тканей Ж. Жаккара (1808) и др.

Возникновение электроники привело к появлению принципиально новых электронных автоматических устройств и целых комплексов — от электронного реле до управляющих вычислительных машин.

По мере развития автоматов расширялись их возможности и области применения, они превратились в сложные автоматические устройства, успешно выполняющие функции контроля, регулирования и управления. Вместо отдельных автоматов стали применяться автоматические комплексы с использованием ЭВМ.

Суффиксный автомат — Википедия

Суффиксный автомат (англ. suffix automaton, directed acyclic word graph, DAWG) — детерминированный конечный автомат (ДКА), принимающий все суффиксы слова S=s1s2…sn{\displaystyle S=s_{1}s_{2}\dots s_{n}} и только их, и обладающий наименьшим возможным числом состояний среди всех таких автоматов. Суффиксный автомат был впервые описан Блумером и др. в 1983 году, они же показали, что размер автомата линеен по длине S{\displaystyle S}, а также предложили онлайн-алгоритм^[en] для его построения с линейным временем работы^[1].

В дальнейших работах на эту тему была обнаружена тесная связь суффиксного автомата с суффиксными деревьями^[2][3], а сама концепция суффиксного автомата подверглась различным обобщениям. Так были введены сжатый суффиксный автомат, получаемый из исходного процедурой сжатия, аналогичной той, которая применяется к суффиксному бору для получения суффиксного дерева^[4], а также обобщённый суффиксный автомат, который строится для набора слов S1,S2,…,Sk{\displaystyle S_{1},S_{2},\dots ,S_{k}} и принимает слова, являющиеся суффиксами хотя бы одного из данных^[5].

С помощью суффиксного автомата можно эффективно решать такие задачи как поиск подстроки в строке, определение наибольшей общей подстроки двух и более строк и другие^[6]. Суффиксные автоматы нашли своё применение в таких прикладных задачах, как сжатие данных^[7], идентификация музыки по записанным фрагментам^[8][9] и сопоставление геномных последовательностей^[10].

Дэвид Хаусслер Ансельм Блумер, на доске изображён CDAWG для строк ababc и abcab

Концепция суффиксного автомата была представлена группой учёных из Денверского и Колорадского университетов Ансельмом Блумером, Анджеем Эренфехтом^[en], Дэвидом Хаусслером^[en], Россом МакКоннеллом и Джанет Блумер в 1983 г., хотя связанные с ним структуры встречались ранее в работах Вайнера^[11], Пратта^[12] и Слисенко^[en][13], посвящённых алгоритмам построения суффиксных деревьев. В той же работе Блумер и др. показали, что построенный по слову S{\displaystyle S} автомат содержит не больше 2|S|−1{\displaystyle 2|S|-1} состояний и не больше 3|S|−4{\displaystyle 3|S|-4} переходов, а также привели линейный алгоритм для его построения^[1].

В 1983 г. Чен и Сейферас независимо разработали алгоритм построения суффиксного автомата, показывающий, что алгоритм Вайнера^[11], предложенный в 1973 г. для построения суффиксного дерева слова S{\displaystyle S}, также строит суффиксный автомат для обращённого слова SR{\textstyle S^{R}} в качестве вспомогательной структуры^[3]. В 1987 г. Блумер и др. по аналогии с суффиксным деревом описали сжатый суффикный автомат (англ. compact directed acyclic word graph, CDAWG)^[4], получаемый из суффиксного автомата удалением состояний с полустепенью исхода, равной единице, а в 1997 г. Крошемор и Верин разработали линейный алгоритм для его непосредственного построения^[14]. В 2001 г. Иненага и др. разработали линейный онлайн-алгоритм для построения сжатого суффиксного автомата^[2], а также линейный алгоритм для построения сжатого суффиксного автомата для набора слов, заданного префиксным деревом^[5].

При описании суффиксных автоматов и связанных с ними фактов и теорем часто используются обозначения из теории формальных языков в целом и теории автоматов в частности^[15]:

• Алфавит — конечное множество Σ{\displaystyle \Sigma }, из которого могут состоять слова. Его элементы называются символами;
• Слово — конечная последовательность символов алфавита: ω=ω1ω2…ωn{\displaystyle \omega =\omega _{1}\omega _{2}\dots \omega _{n}}, где ωk∈Σ{\displaystyle \omega _{k}\in \Sigma } для k=1..n{\displaystyle k=1..n}. Длина слова ω{\displaystyle \omega } обозначается как |ω|=n{\displaystyle |\omega |=n};
• Множество всех слов обозначается как Σ∗{\displaystyle \Sigma ^{*}}(здесь символ «*» несёт смысл звезды Клини), пустое слово (слово нулевой длины) — символом ε{\displaystyle \varepsilon };
• Конкатенация (произведение) слов α=α1α2…αn{\displaystyle \alpha =\alpha _{1}\alpha _{2}\dots \alpha _{n}} и β=β1β2…βm{\displaystyle \beta =\beta _{1}\beta _{2}\dots \beta _{m}} обозначается как α⋅β{\displaystyle \alpha \cdot \beta } или αβ{\displaystyle \alpha \beta } и равна слову, получаемому приписыванием β{\displaystyle \beta } к α{\displaystyle \alpha } справа, то есть, αβ=α1α2…αnβ1β2…βm{\displaystyle \alpha \beta =\alpha _{1}\alpha _{2}\dots \alpha _{n}\beta _{1}\beta _{2}\dots \beta _{m}};
• Если слово ω∈Σ{\displaystyle \omega \in \Sigma } представимо в виде ω=αγβ{\displaystyle \omega =\alpha \gamma \beta }, где α,β,γ∈Σ∗{\displaystyle \alpha ,\beta ,\gamma \in \Sigma ^{*}}, то слова α{\displaystyle \alpha }, β{\displaystyle \beta } и γ{\displaystyle \gamma } называют префиксом, суффиксом и подсловом (подстрокой) слова ω{\displaystyle \omega } соответственно;
• Правым контекстом слова ω{\displaystyle \omega } относительно языка L{\displaystyle L} называют множество [ω]R={α:ωα∈L}{\displaystyle [\omega ]_{R}=\{\alpha :\omega \alpha \in L\}}. То есть это множество слов α{\displaystyle \alpha }, при приписывании которых к слову ω{\displaystyle \omega } справа получается слово из языка L{\displaystyle L};
• Правые контексты индуцируют естественное отношение эквивалентности ≡R{\displaystyle \equiv _{R}} на множестве всех слов такое что α≡Rβ⟺[α]R=[β]R{\displaystyle \alpha \equiv _{R}\beta \iff [\alpha ]_{R}=[\beta ]_{R}}. Если α≡Rβ{\displaystyle \alpha \equiv _{R}\beta }, то про них говорят, что они правоэквивалентны.

Как и любой конечный автомат, суффиксный автомат, заданный формальной пятёркой A=(Σ,Q,q0,F,δ){\displaystyle {\mathcal {A}}=(\Sigma ,Q,q_{0},F,\delta )}, может быть представлен в виде ориентированного графа (диаграммы) такого что^[16]:

• Множество вершин графа соответствует множеству состояний автомата Q{\displaystyle Q},
• В графе выделена некоторая вершина, соответствующая начальному состоянию q0∈Q{\displaystyle q_{0}\in Q},
• В графе выделен набор вершин, соответствующих множеству финальных состояний F⊂Q{\displaystyle F\subset Q},
• Множество дуг в графе соответствует множеству переходов δ⊂Q×Σ×Q{\displaystyle \delta \subset Q\times \Sigma \times Q}, которое состоит из троек (q1,σ,q2){\displaystyle (q_{1},\sigma ,q_{2})}, где q1,q2∈Q{\displaystyle q_{1},q_{2}\in Q} и σ∈Σ{\displaystyle \sigma \in \Sigma } (см. декартово произведение),
• При этом переходу (q1,σ,q2)∈δ{\textstyle (q_{1},\sigma ,q_{2})\in \delta } соответствует дуга из q1{\displaystyle q_{1}} в q2{\displaystyle q_{2}}, помеченная символом алфавита σ{\displaystyle \sigma }. Такой переход также обозначают как q1σ⟶q2{\textstyle q_{1}{\begin{smallmatrix}{\sigma }\\[-5pt]{\longrightarrow }\end{smallmatrix}}q_{2}}.

В таком графе вершины и дуги отождествляются с состояниями и переходами автомата соответственно. В таком естественном представлении автомат принимает слово ω=ω1ω2…ωm{\displaystyle \omega =\omega _{1}\omega _{2}\dots \omega _{m}} в том и только том случае, если существует путь из начального состояния q0{\displaystyle q_{0}} в некоторое финальное состояние q∈F{\displaystyle q\in F} такой, что если сконкатенировать символы, встретившиеся на этом пути, то получится слово ω{\displaystyle \omega }^[15].

Состояния автомата[править | править код]

Для конечных автоматов имеет место утверждение, следующее из теоремы Майхилла — Нероуда^[17][18]:

В случае суффиксного автомата язык L{\displaystyle L} состоит из суффиксов слова S=s1s2…sn{\displaystyle S=s_{1}s_{2}\dots s_{n}}, поэтому правый контекст слова ω{\displaystyle \omega } состоит из слов α{\displaystyle \alpha } таких что ωα{\displaystyle \omega \alpha } — суффикс S{\displaystyle S}. Это позволяет сформулировать следующую лемму^[19][20]:

Из этого следует ряд структурных свойств состояний суффиксного автомата и слов, которые ими принимаются. Пусть |α|≤|β|{\displaystyle |\alpha |\leq |\beta |}, тогда^[20]:

Таким образом, любое состояние q=[α]R{\displaystyle q=[\alpha ]_{R}} суффиксного автомата принимает некоторую непрерывную цепочку вложенных друг в друга суффиксов наибольшей строки из этого состояния^[20].

Левым расширением α←{\displaystyle {\overset {\scriptstyle {\leftarrow }}{\alpha }}} строки α{\displaystyle \alpha } называют самую длинную строку ω{\displaystyle \omega }, имеющую тот же правый контекст. Длину |α←|{\displaystyle |{\overset {\scriptstyle {\leftarrow }}{\alpha }}|} самой длинной строки, принимаемой состоянием q=[α]R{\displaystyle q=[\alpha ]_{R}}, обозначают как len(q){\displaystyle len(q)}.

Cуффиксной ссылкой link(q){\displaystyle link(q)} от состояния q=[α]R{\displaystyle q=[\alpha ]_{R}} называют указатель на состояние p{\displaystyle p}, содержащее наибольший суффикс α{\displaystyle \alpha }, который не принимается состоянием q{\displaystyle q}.

В таких обозначениях можно сказать, что состояние q=[α]R{\displaystyle q=[\alpha ]_{R}} принимает в точности все суффиксы α←{\displaystyle {\overset {\scriptstyle {\leftarrow }}{\alpha }}}, которые длиннее len(link(q)){\displaystyle len(link(q))} и не длиннее len(q){\displaystyle len(q)}. Кроме того, верно следующее^[21]: