Логический вентиль — Википедия

Материал из Википедии — свободной энциклопедии

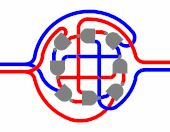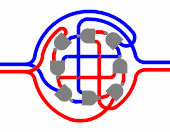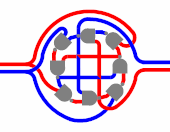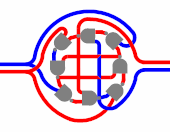Пример работы схемы двухступенчатого T-триггера с парафазным входом на двух парафазных D-триггерах на восьми логических вентилях 2И-НЕ. Слева — входы, справа — выходы. Синий цвет соответствует 0, красный — 1

Логи́ческий ве́нтиль — базовый элемент цифровой схемы, выполняющий элементарную логическую операцию^[1], преобразуя таким образом множество входных логических сигналов в выходной логический сигнал. Логика работы вентиля основана на битовых операциях^[2] с входными цифровыми сигналами в качестве операндов. При создании цифровой схемы вентили соединяют между собой, при этом выход используемого вентиля должен быть подключён к одному или к нескольким входам других вентилей. В настоящее время в созданных человеком цифровых устройствах доминируют электронные логические вентили на базе полевых транзисторов, однако в прошлом для создания вентилей использовались и другие устройства, например, электромагнитные реле, гидравлические устройства, а также механические устройства. В поисках более совершенных логических вентилей исследуются квантовые устройства

[3]^[4], биологические молекулы^[5], фононные тепловые системы^[6].

В цифровой электронике логический уровень сигнала представлен в виде уровня напряжения (попадающего в один из двух диапазонов) или в виде значения тока. Это зависит от типа используемой технологии построения электронной логики^[7]. Поэтому любой тип электронного вентиля требует наличия питания для приведения выходного сигнала к необходимому уровню.

Впервые математически точно двоичная система счисления была подробно описана немецким математиком Готфридом Вильгельмом Лейбницем (публикация от 1705 года). Он также разъяснил, как с помощью этой системы можно объединить принципы арифметики и логики.

Первые логические вентили были реализованы механически. В 1837 году английский изобретатель Чарльз Бэббидж разработал вычислительную машину, названную им аналитической (англ. Analytical Engine), которая считается прообразом современного компьютера.

В 1847 году английский математик и логик Джордж Буль в своём трактате «Математический анализ логики» (англ. The Mathematical Analysis of Logic) заложил основы современной алгебры логики, связав её с логикой высказываний. При этом он ввёл свою алгебраическую систему, которая содержала следующие функции: конъюнкция (логическое умножение, оператор «AND»), дизъюнкция (логическое сложение, оператор «OR») и отрицание (оператор «NOT»). Впоследствии данная алгебра была названа булевой.

В том же 1847 году шотландский математик и логик Огастес де Морган опубликовал правила, связывающие пары логических операций при помощи логического отрицания (Законы де Моргана).

В 1881 г. американский математик и логик Чарльз Сандерс Пирс теоретически доказал, что функция «инверсия дизъюнкции» является универсальной и позволяет заменить все другие логические функции. Данная функция получила имя «функция Пирса», знак операции — стрелка Пирса ↓. Позже, элемент, реализующий данную функцию, стали называть

элементом Пирса или «ИЛИ-НЕ» (англ. NOR gate, см. таблицу). Данная работа была опубликована только в 1933 году.

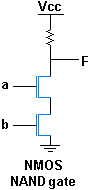
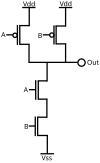
В 1913 г. американский математик и логик Генри Морис Шеффер теоретически доказал, что функция «инверсия конъюнкции» является универсальной и позволяет заменить все другие логические функции. Данная функция получила имя «функция Шеффера», знак операции — штрих Шеффера |. Позже элемент, реализующий данную функцию, стали называть элементом Шеффера или «И-НЕ» (англ. NAND gate, см. таблицу).

В 1927 г. российский советский математик и логик Иван Иванович Жегалкин представил алгебру логики как арифметику вычетов по модулю 2. Данная универсальная функция получила позднее название «полином Жегалкина», а знак операции — ⊕{\displaystyle \oplus }. Позже элемент, реализующий данную функцию, стали называть «исключающее ИЛИ» (англ. XOR gate).

В 1935 г. немецкий инженер Конрад Цузе разрабатывает для своей вычислительной машины Z1 первые действующие электромеханические вентили.

В 1906 г. американский изобретатель Ли де Форест вводит в вакуумную лампу Джона Флеминга третий электрод — управляющую сетку и получает триод, который может работать не только в качестве усилителя электрических сигналов, но и в качестве простейшего переключателя (вентиля).

В 1947 г. Уильям Шокли, Джон Бардин и Уолтер Браттейн в лабораториях Bell Labs впервые создают действующий биполярный транзистор. Позднее транзисторы заменили вакуумные лампы в большинстве электронных устройств, совершив революцию в создании интегральных схем.

ТТЛ 2И-НЕ вентиль

КМОП 2И-НЕ вентиль на кристалле в микросхеме

1. ↑ gpntb.ru — Термины микроэлекроники
2. ↑ Например: 2И-НЕ (NAND), XOR (исключающее ИЛИ) и другие.
3. ↑ scientific.ru — Квантовый логический вентиль на сверхпроводниках
4. ↑ pereplet.ru — Спиновые логические вентили на основе квантовых точек
5. ↑ skms.impb.psn.ru — Электронный логический вентиль XOR на основе ДНК.
6. ↑ Wang, Lei and Li, Baowen.
   Thermal Logic Gates: Computation with Phonons (англ.) // Physical Review Letters. — APS, 2007. — Vol. 99, no. 17.
7. ↑ Наиболее известные это КМОП, ТТЛ, N-МОП, ЭСЛ, ДТЛ, РТЛ.

6 Лекция: Логические вентили, схемы, структуры

Рассматриваются основные теоретические (математические, логические) понятия и сведения, касающиеся базовых логических элементов и структур – логических вентилей, логических (переключательных) схем, логической базы аппаратуры ЭВМ и их оптимальной структуры, оптимизации их структур.

Любой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит их простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых

вентилей (логических устройств, базовых логических схем), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули.

Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам.

Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов (вентилей, логических схем или так называемых переключательных схем). Они воспроизводят функции полупроводниковых схем.

Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике).

Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором.

Логическая функция «инверсия», или отрицание, реализуется логической схемой (вентилем), называемой инвертор.

Принцип его работы можно условно описать следующим образом: если, например, «0» или «ложь» отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или «истина», которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт.

Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт («истина»), то на выходе инвертора будет сниматься 0 вольт, то есть «ложь» (схемы на рисунке 1 ).

Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рис. 2), в которой замкнутая цепь соответствует 1 («истина») или х = 1, а размыкание цепи соответствует 0 («ложь») или х = 0.

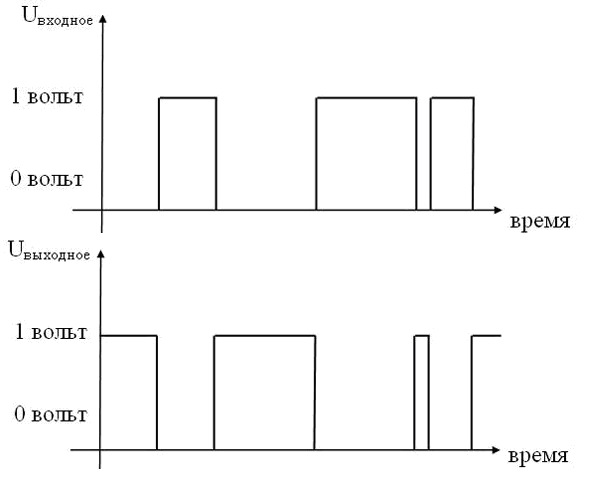
Рис. 1.  Принцип работы инвертора

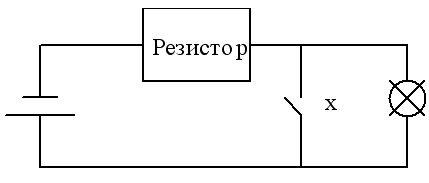
Рис. 2.  Электрический аналог схемы инвертора

Дизъюнкцию реализует логическое устройство (вентиль) называемое дизьюнктор (рис. 3):

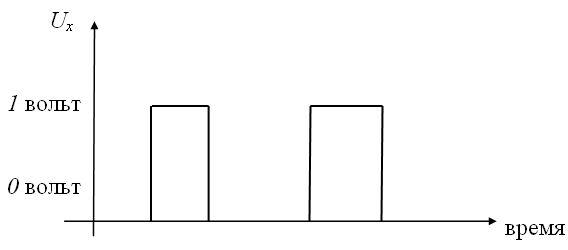
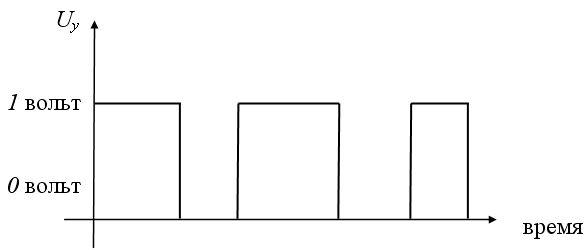
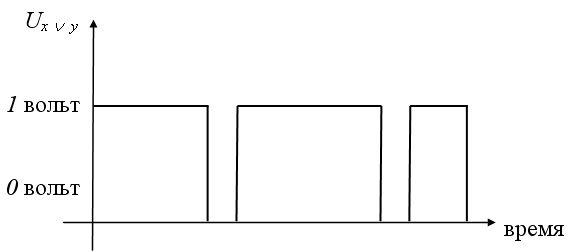
Рис. 3.  Принцип работы дизъюнктора

Дизъюнктор условно изображается схематически электрической цепью вида (рис. 4)

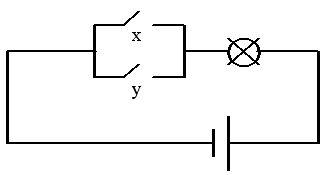
Рис. 4.  Электрический аналог схемы дизъюнктора

Конъюнкцию 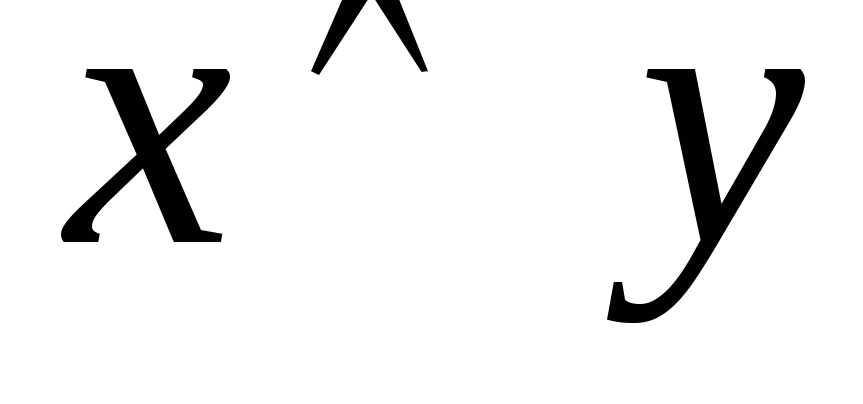реализуетлогическая схема (вентиль), называемая конъюнктором (рис. 5):

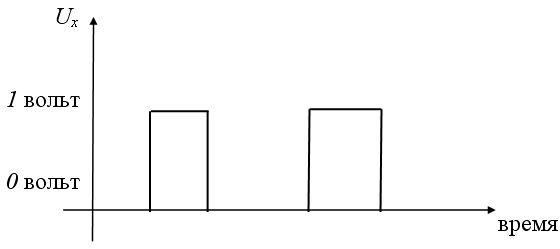
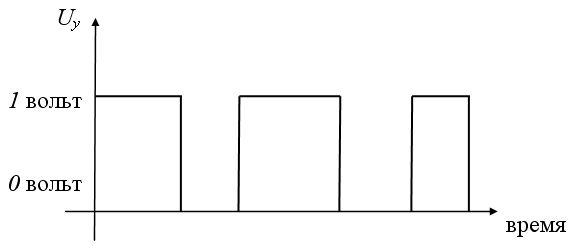
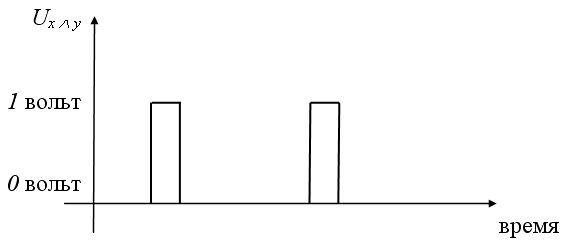
Рис. 5.  Принцип работы конъюнктора

Конъюнктор можно условно изобразить схематически электрической цепью вида (рис. 6.6)

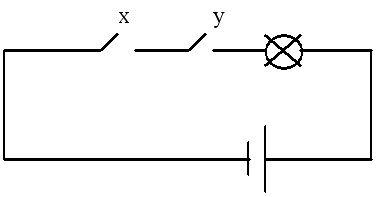
Рис. 6.  Электрический аналог схемы конъюнктора

Схематически инвертор, дизъюнктор и конъюнктор на логических схемах различных устройств можно изображать условно следующим образом (рис. 7). Есть и другие общепринятые формы условных обозначений.

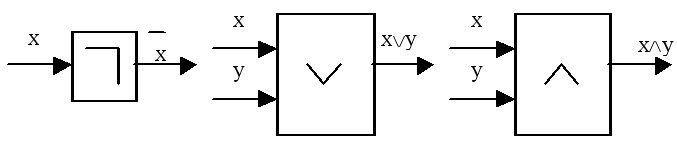
Рис. 7.  Условные обозначения вентилей (вариант)

Из указанных простейших базовых логических элементов собирают, конструируют сложные логические схемы ЭВМ, например, сумматоры, шифраторы, дешифраторы и др. Большие (БИС) и сверхбольшие (СБИС) интегральные схемы содержат в своем составе (на кристалле кремния площадью в несколько квадратных сантиметров) десятки тысяч вентилей. Это возможно еще и потому, что базовый набор логических схем (инвертор, конъюнктор, дизъюнктор) является функционально полным (любую логическую функцию можно представить через эти базовые вентили), представление логических констант в них одинаково (одинаковы электрические сигналы, представляющие 1 и 0) и различные схемы можно «соединять» и «вкладывать» друг в друга (осуществлять композицию и суперпозицию схем).

Таким способом конструируются более сложные узлы ЭВМ – ячейки памяти, регистры, шифраторы, дешифраторы, а также сложнейшие интегральные схемы.

Пример. В двоичной системе таблицу суммирования цифры x и цифры y и получения цифры z с учетом переноса p в некотором разряде чисел x и y можно изобразить таблицей вида

x	y	z	p
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Эту таблицу можно интерпретировать как совместно изображаемую таблицу логических функций (предикатов) вида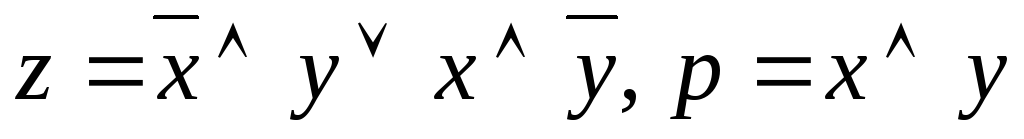

Логический элемент, соответствующий этим функциям, называется одноразрядным сумматором и имеет следующую схему (обозначим ее как или– если мы хотим акцентировать именно выбранный, текущийi-й разряд) (рис. 8):

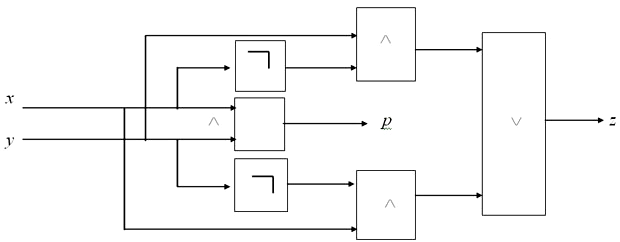
Рис. 8.  Схема одноразрядного сумматора

Пример. «Черным ящиком» называется некоторое закрытое устройство (логическая, электрическая или иная схема), содержимое которого неизвестно и может быть определено (идентифицировано) только по отдельным проявлениям входа/выхода ящика (значениям входных и выходных сигналов). В «черном ящике» находится некоторая логическая схема, которая в ответ на некоторую последовательность входных (для ящика) логических констант выдает последовательность логических констант, получаемых после выполнения логической схемы внутри «черного ящика». Определим логическую функцию внутри «черного ящика» (рис. 9), если операции выполняются с логическими константами для входных последовательностей (поразрядно). Например, х = 00011101 соответствует последовательности поступающих значений: «ложь», «ложь», «ложь», «истина», «истина», «истина», «ложь», «истина».

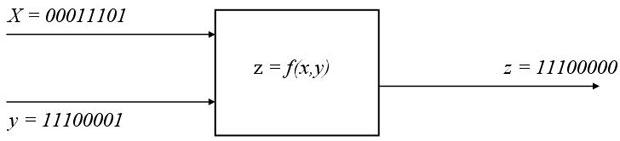
Рис. 9.  Схема «черного ящика 1»

Из анализа входных значений (входных сигналов) х, у и поразрядного сравнения логических констант в этих сообщениях с константами в значении z – результате выполнения функции в «черном ящике», видно, что подходит, например, функция вида .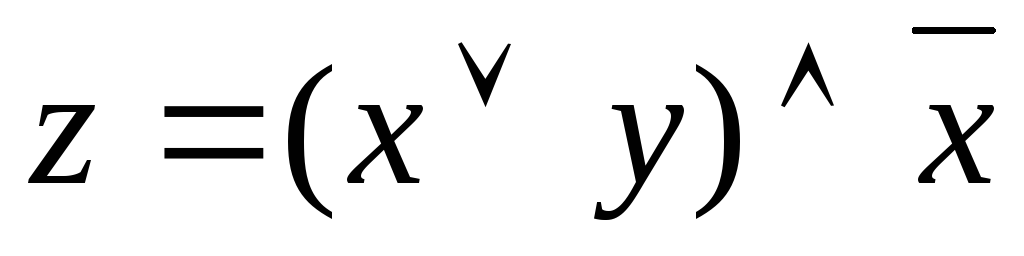

Действительно, в результате «поразрядного» сравнения сигналов (последовательностей значений «истина», «ложь») получаем следующие выражения (последовательности логических констант):

.

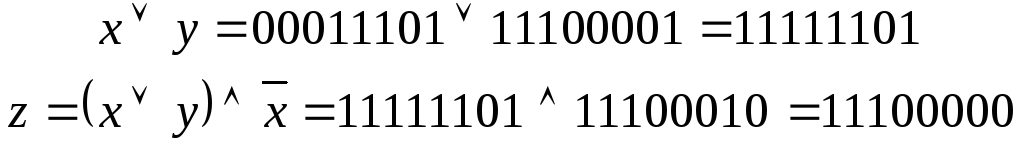Пример. Попробуйте самостоятельно выписать функцию для «черного ящика»? указанного на рис. 10:

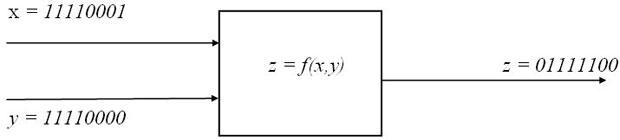
Рис. 10.  Схема «черного ящика 2»

Важной задачей (технической информатики) является минимизация числа вентилей для реализации той или иной схемы (устройства), что необходимо для более рационального, эффективного воплощения этих схем, для большей производительности и меньшей стоимости ЭВМ.

Эту задачу решают с помощью методов теоретической информатики (методов булевой алгебры).

Пример. Построим схему для логической функции 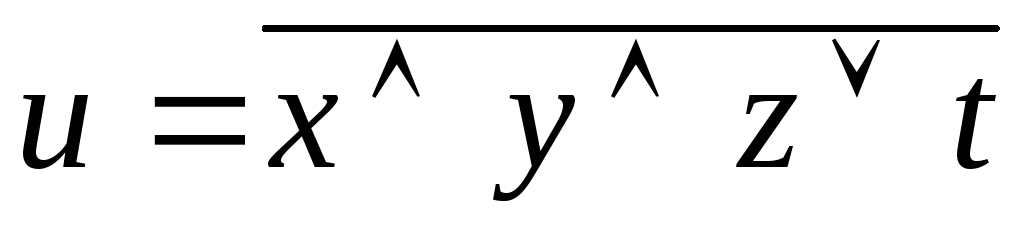. Схема, построенная для этой логической функции, приведена на рис. 11.

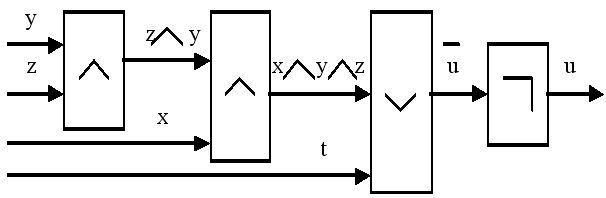
Рис. 11.  Схема для функции 1

Пример. Определим логическую функцию 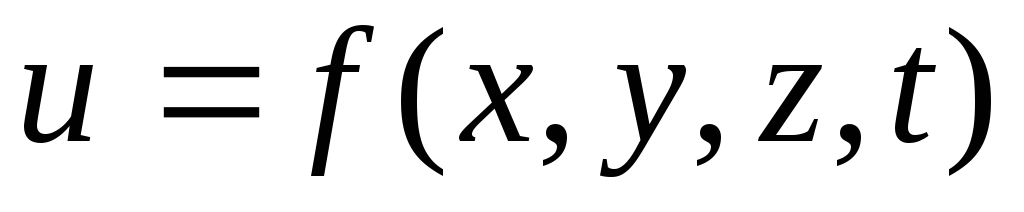, реализуемую логической схемой вида (рис. 12):

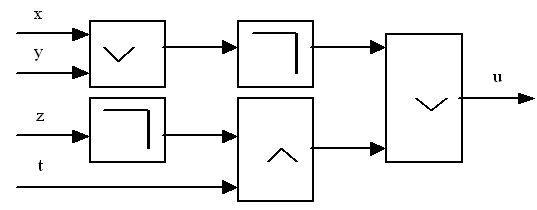
Рис. 12.  Схема для функции 2

Искомая логическая функция, если выписать ее последовательно, заполняя «верх» каждой стрелки, будет иметь следующий вид: .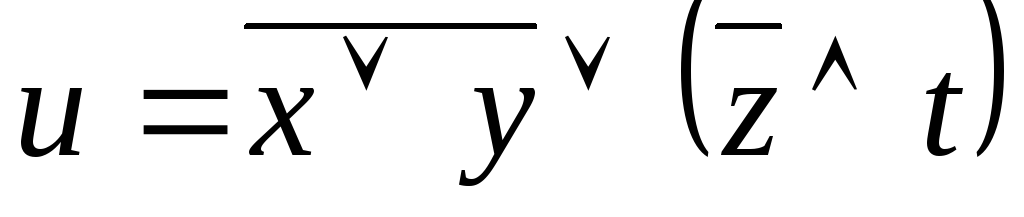

Логические вентили | Теория

Символы и таблицы истинности для базовых логических вентилей показаны на рисунке. Таблица истинности описывает, какой комбинации входных сигналов будет соответствовать определенный выходной сигнал.

Схема «И» (AND) будет генерировать выходной логический сигнал «1», сели оба входных сигнала также имеют уровень «1». Другими словами: выход равен «1», когда входные сигналы в выражении «А И В» равны «1».

Рис. Логические вентили и их таблицы истинности

Схема «ИЛИ» (OR) формирует выход «1» по выражению «А ИЛИ В», когда один или оба входных сигнала равны «1». Опять же для этой схемы могут быть использованы более двух входов.

Схема «НЕ» (NOT) является очень простым прибором, где выходной сигнал всегда будет находиться в противоположном логическом состоянии, нежели входной сигнал. В этом случае вход и выход связаны как «А = NOT В» и, конечно же, этот прибор имеет только один вход и один выход.

Каждая из схем И и ИЛИ может бить скомбинирована с вентилем НЕ, чтобы образовать схему И-НЕ (NAND) и схему ИЛИ-НЕ (NOR), соответственно. Оказалось, что эти две схемы являются наиболее универсальными и позволяют конструировать сложные логические цепи. Выходной сигнал этих схем есть инверсия выходного сигнала первоначальных схем И и ИЛИ.

Наконец, схема, известная как «исключающее ИЛИ» (XOR), может иметь только два входа. Эта схема будет формировать выходной сигнал «1», когда выполнятся условие А ИЛИ В, но при этом ни один из входных сигналов не равен другому.

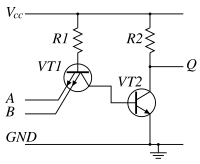
Презентация на тему: Вентиль «И-НЕ», NAND

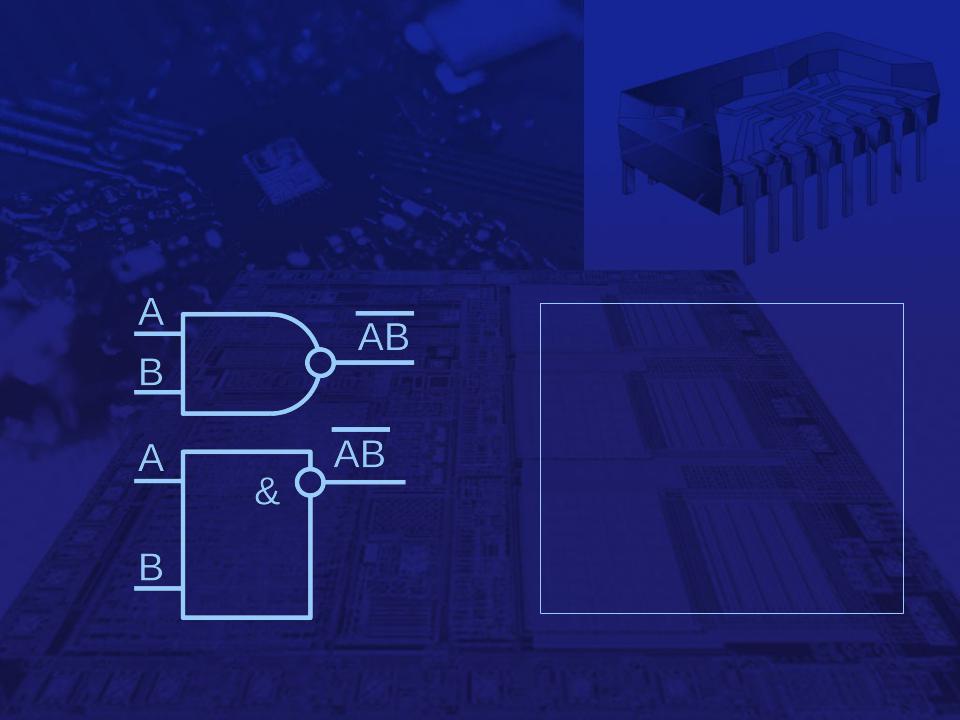
Графическое

обозначение

Таблица

истинности

A	В
		AВ
0	0	1
0	1	1
1	0	1
1	1	0

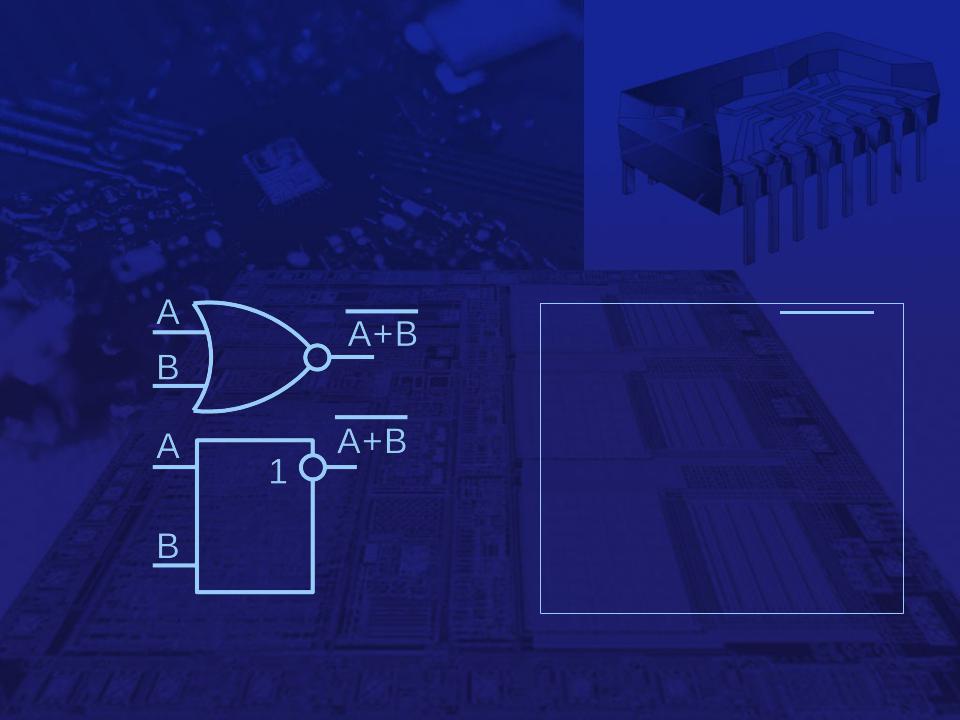
Вентиль «ИЛИ-НЕ», NOR

Графическое

обозначение

Таблица

истинности

AВ A+В

Универсальные вентили «И-НЕ», «ИЛИ-НЕ»

	НЕ
И-НЕ	И
	ИЛИ
	НЕ
ИЛИ-НЕ	И
	ИЛИ

A = AA

AB = (AB) = (AB)(AB)

A + B = AB = (AA)(BB)

A = A + A

AB = A+B = (A+A)+(B+B) A+B = (A+B) = (A+B)+(A+B)

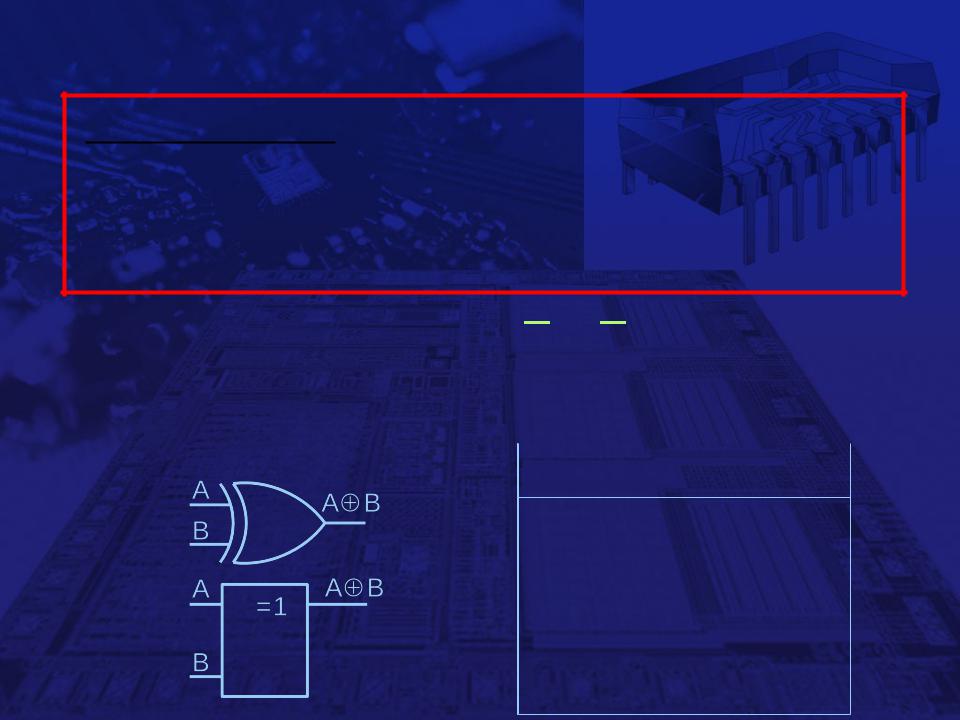
Вентиль «Исключающее ИЛИ»

Определение: результат операции исключающее ИЛИ (Exclusive OR), выполняемой над двумя переменными А и В, равен 0, если А=В, иначе результат равен 1.

A В = AB + AB

Графическое обозначение Таблица истинности

A	В	A В
0	0	0
0	1	1
1	0	1
1	1	0

Вентиль «Исключающее ИЛИ-НЕ»

Определение: результат операции исключающее ИЛИ-НЕ (Exclusive NOR), выполняемой над двумя переменными А и В, равен 1, если А=В, иначе результат равен 0.

(A В) = AB + AB

	Графическое	Таблица истинности
	обозначение
		A	В	A В
		0	0	1
		0	1	0
		1	0	0
		1	1	1

Коммутативные функции

A B F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 F13 F14 F15

0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

F1 – операция И

F6 – операция исключающее ИЛИ

F7 – операция ИЛИ

F8 – операция ИЛИ-НЕ

F9 – операция исключающее ИЛИ-НЕ

F14 – операция И-НЕ

Итоги:

Входе лекции изучены:

–Базовые логические функции и вентили: И, ИЛИ, НЕ

–Основные тождества и правила булевой алгебры.

–Положительная и отрицательная логика.

–Принцип дуализма логических функций и правило де Моргана.

–Универсальные вентили: И-НЕ, ИЛИ-НЕ

–Функции «Исключающего ИЛИ» и «Исключающего ИЛИ-НЕ»

–Полный набор логических функция для двух переменных.

Логический вентиль — Википедия

Материал из Википедии — свободной энциклопедии

Пример работы схемы двухступенчатого T-триггера с парафазным входом на двух парафазных D-триггерах на восьми логических вентилях 2И-НЕ. Слева — входы, справа — выходы. Синий цвет соответствует 0, красный — 1

Логи́ческий ве́нтиль — базовый элемент цифровой схемы, выполняющий элементарную логическую операцию^[1], преобразуя таким образом множество входных логических сигналов в выходной логический сигнал. Логика работы вентиля основана на битовых операциях^[2] с входными цифровыми сигналами в качестве операндов. При создании цифровой схемы вентили соединяют между собой, при этом выход используемого вентиля должен быть подключён к одному или к нескольким входам других вентилей. В настоящее время в созданных человеком цифровых устройствах доминируют электронные логические вентили на базе полевых транзисторов, однако в прошлом для создания вентилей использовались и другие устройства, например, электромагнитные реле, гидравлические устройства, а также механические устройства. В поисках более совершенных логических вентилей исследуются квантовые устройства^[3][4], биологические молекулы^[5], фононные тепловые системы^[6].

В цифровой электронике логический уровень сигнала представлен в виде уровня напряжения (попадающего в один из двух диапазонов) или в виде значения тока. Это зависит от типа используемой технологии построения электронной логики^[7]. Поэтому любой тип электронного вентиля требует наличия питания для приведения выходного сигнала к необходимому уровню.

История

Впервые математически точно двоичная система счисления была подробно описана немецким математиком Готфридом Вильгельмом Лейбницем (публикация от 1705 года). Он также разъяснил, как с помощью этой системы можно объединить принципы арифметики и логики.

Первые логические вентили были реализованы механически. В 1837 году английский изобретатель Чарльз Бэббидж разработал вычислительную машину, названную им аналитической (англ. Analytical Engine), которая считается прообразом современного компьютера.

В 1847 году английский математик и логик Джордж Буль в своём трактате «Математический анализ логики» (англ. The Mathematical Analysis of Logic) заложил основы современной алгебры логики, связав её с логикой высказываний. При этом он ввёл свою алгебраическую систему, которая содержала следующие функции: конъюнкция (логическое умножение, оператор «AND»), дизъюнкция (логическое сложение, оператор «OR») и отрицание (оператор «NOT»). Впоследствии данная алгебра была названа булевой.

В том же 1847 году шотландский математик и логик Огастес де Морган опубликовал правила, связывающие пары логических операций при помощи логического отрицания (Законы де Моргана).

В 1881 г. американский математик и логик Чарльз Сандерс Пирс теоретически доказал, что функция «инверсия дизъюнкции» является универсальной и позволяет заменить все другие логические функции. Данная функция получила имя «функция Пирса», знак операции — стрелка Пирса ↓. Позже, элемент, реализующий данную функцию, стали называть элементом Пирса или «ИЛИ-НЕ» (англ. NOR gate, см. таблицу). Данная работа была опубликована только в 1933 году.

В 1913 г. американский математик и логик Генри Морис Шеффер теоретически доказал, что функция «инверсия конъюнкции» является универсальной и позволяет заменить все другие логические функции. Данная функция получила имя «функция Шеффера», знак операции — штрих Шеффера |. Позже элемент, реализующий данную функцию, стали называть элементом Шеффера или «И-НЕ» (англ. NAND gate, см. таблицу).

В 1927 г. российский советский математик и логик Иван Иванович Жегалкин представил алгебру логики как арифметику вычетов по модулю 2. Данная универсальная функция получила позднее название «полином Жегалкина», а знак операции — ⊕{\displaystyle \oplus }. Позже элемент, реализующий данную функцию, стали называть «исключающее ИЛИ» (англ. XOR gate).

В 1935 г. немецкий инженер Конрад Цузе разрабатывает для своей вычислительной машины Z1 первые действующие электромеханические вентили.

В 1906 г. американский изобретатель Ли де Форест вводит в вакуумную лампу Джона Флеминга третий электрод — управляющую сетку и получает триод, который может работать не только в качестве усилителя электрических сигналов, но и в качестве простейшего переключателя (вентиля).

В 1947 г. Уильям Шокли, Джон Бардин и Уолтер Браттейн в лабораториях Bell Labs впервые создают действующий биполярный транзистор. Позднее транзисторы заменили вакуумные лампы в большинстве электронных устройств, совершив революцию в создании интегральных схем.

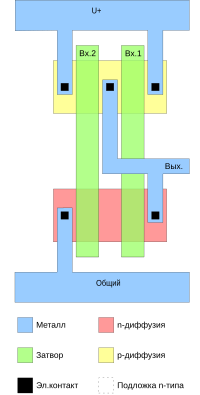
Логические вентили

Реализация

ТТЛ 2И-НЕ вентиль

КМОП 2И-НЕ вентиль на кристалле в микросхеме

Примечания

1. ↑ gpntb.ru — Термины микроэлекроники
2. ↑ Например: 2И-НЕ (NAND), XOR (исключающее ИЛИ) и другие.
3. ↑ scientific.ru — Квантовый логический вентиль на сверхпроводниках
4. ↑ pereplet.ru — Спиновые логические вентили на основе квантовых точек
5. ↑ skms.impb.psn.ru — Электронный логический вентиль XOR на основе ДНК.
6. ↑ Wang, Lei and Li, Baowen. Thermal Logic Gates: Computation with Phonons (англ.) // Physical Review Letters. — APS, 2007. — Vol. 99, no. 17.
7. ↑ Наиболее известные это КМОП, ТТЛ, N-МОП, ЭСЛ, ДТЛ, РТЛ.

См. также

НОУ ИНТУИТ | Лекция | Логические вентили, схемы, структуры

Аннотация: Рассматриваются основные теоретические (математические, логические) понятия и сведения, касающиеся базовых логических элементов и структур – логических вентилей, логических (переключательных) схем, логической базы аппаратуры ЭВМ и их оптимальной структуры, оптимизации их структур.

Любой, самый примитивный компьютер – сложнейшее техническое устройство. Но даже такое сложное устройство, как и все в природе и в технике, состоит из простейших элементов. Любой компьютер, точнее, любой его электронный логический блок состоит из десятков и сотен тысяч так называемых вентилей (логических устройств, базовых логических схем ), объединяемых по правилам и законам (аксиомам) алгебры вентилей в схемы, модули.

Логический вентиль (далее – просто вентиль) – это своего рода атом, из которого состоят электронные узлы ЭВМ. Он работает по принципу крана (отсюда и название), открывая или закрывая путь сигналам.

Логические схемы предназначены для реализации различных функций алгебры логики и реализуются с помощью трех базовых логических элементов ( вентилей, логических схем или так называемых переключательных схем ). Они воспроизводят функции полупроводниковых схем.

Работу вентильных, логических схем мы, как и принято, будем рассматривать в двоичной системе и на математическом, логическом уровне, не затрагивая технические аспекты (аспекты микроэлектроники, системотехники, хотя они и очень важны в технической информатике).

Логические функции отрицания, дизъюнкции и конъюнкции реализуют, соответственно, логические схемы, называемые инвертором, дизъюнктором и конъюнктором.

Логическая функция «инверсия», или отрицание, реализуется логической схемой ( вентилем ), называемой инвертор.

Принцип его работы можно условно описать следующим образом: если, например, «0» или «ложь» отождествить с тем, что на вход этого устройства скачкообразно поступило напряжение в 0 вольт, то на выходе получается 1 или «истина», которую можно также отождествить с тем, что на выходе снимается напряжение в 1 вольт.

Аналогично, если предположить, что на входе инвертора будет напряжение в 1 вольт («истина»), то на выходе инвертора будет сниматься 0 вольт, то есть «ложь» ( схемы на рисунках 6.1 а, б).

Рис. 6.1. Принцип работы инвертора

Функцию отрицания можно условно отождествить с электрической схемой соединения в цепи с лампочкой (рис. 6.2), в которой замкнутая цепь соответствует 1 («истина») или х = 1, а размыкание цепи соответствует 0 («ложь») или х = 0.

Рис. 6.2. Электрический аналог схемы инвертора

Дизъюнкцию реализует логическое устройство ( вентиль ) называемое дизьюнктор (рис. 6.3 а, б, в):

Рис. 6.3a.
Рис. 6.3b.
Рис. 6.3c. Принцип работы дизъюнктора

Дизъюнктор условно изображается схематически электрической цепью вида (рис. 6.4)

Рис. 6.4. Электрический аналог схемы дизъюнктора

Конъюнкцию реализует логическая схема ( вентиль ), называемая конъюнктором (рис. 6.5 а, б, в):

Рис. 6.5a.
Рис. 6.5b.
Рис. 6.5c. Принцип работы конъюнктора

Гидравлические и пневматические схемы — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2018; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 ноября 2018; проверки требует 1 правка. Простейшая принципиальная гидравлическая схема гидропривода (код Г3)

Гидравли́ческая (пневмати́ческая) схе́ма — это технический документ, содержащий в виде условных графических изображений или обозначений информацию о строении изделия, его составных частях и взаимосвязи между ними, действие которого основывается на использовании энергии сжатой жидкости (газа). Гидравлическая схема является одним из видов схем изделий и обозначаются в шифре основной надписи литерой «Г» (пневматическая — литерой «П»)^[1].

Гидравлические и пневматические схемы в зависимости от их основного назначения подразделяются на следующие типы^[2]:

Структурные гидравлические (пневматические) схемы[править | править код]

На структурной схеме элементы и устройства изображают в виде прямоугольников, внутри которых вписывают наименование соответствующей функциональной части. Все элементы связаны между собой линиями взаимосвязи (сплошные основные линии), на которых принято указывать направления потоков рабочей среды по ГОСТ 2.721-68^[3] Графическое построение схемы должно давать как можно более наглядное представление о последовательности взаимодействия функциональных частей в изделии.

При большом количестве функциональных частей допускается вместо наименований, типов и обозначений проставлять порядковые номера справа от изображения или над ним, как правило, сверху вниз в направлении слева направо. В этом случае наименования, типы и обозначения указывают в таблице, которую располагают на полях схемы. Этот вид схем обозначаются в шифре основной надписи символами Г1 (или П1, для пневматических).

Принципиальные гидравлические (пневматические) схемы[править | править код]

На принципиальной схеме изображают все гидравлические (пневматические) элементы или устройства, необходимые для осуществления и контроля в изделии заданных гидравлических (пневматических) процессов, и все гидравлические (пневматические) связи между ними. При этом используются графические условные обозначения:

Каждый элемент должен иметь позиционное обозначение, которое состоит из литерного обозначения и порядкового номера. Литерное обозначение должно представлять собой укороченное наименование элемента, составленное из его начальных или характерных букв, например: клапан — К, дроссель — ДР. Порядковые номера элементов (устройств) следует присваивать, начиная с единицы, в границах группы элементов (устройств), которым на схеме присвоено одинаковое литерное позиционное обозначение, например, Р1, Р2, Р3 и т.д., К1, К2, К3 и т.д.

Литерные позиционные обозначения основных элементов^[2]:

На принципиальной схеме должны быть однозначно обозначены все элементы, входящие в состав изделия и изображённые на схеме.

Данные об элементах должны быть занесены в перечень элементов. При этом связь перечня с условными графическими обозначениями элементов должна осуществляться через позиционные обозначения. Перечень элементов размещают на первом листе схемы или выполняют в виде самостоятельного документа.

Эти схемы обозначаются в шифре основной надписи символами Г3 (П3′).

На схемах соединений кроме всех гидравлических и пневматических элементов показывают также трубопроводы и элементы соединений трубопроводов. При этом соединения трубопроводов показывают в виде упрощённых внешних очертаний, а сами трубопроводы — сплошными основными линиями.

Расположение графических обозначений элементов и устройств на схеме должно приблизительно отвечать действительному размещению элементов и устройств в изделии. Допускается на схеме не показывать расположение элементов и устройств в изделии, если схему выполняют на нескольких листах или расположение элементов и устройств на месте эксплуатации неизвестно.

На схеме возле графических обозначений элементов и устройств указывают позиционные обозначения, присвоенные им на принципиальной схеме. Возле или внутри графического обозначения устройства и рядом с графическим обозначением элемента допускается указывать его наименование и тип и (или) обозначение документа, на основании которого устройство использовано, номинальные значения основных параметров (давление, подача, расход и т.п.).

Эти схемы обозначаются в шифре основной надписи символами Г4 (П4).

1. ↑ ГОСТ 2.701-2008 Единая система конструкторской документации. Схемы. Виды и типы. Общие требования к выполнению.
2. ↑ ^{1 2} ГОСТ 2.704-76 Единая система конструкторской документации. Правила выполнения гидравлических и пневматических схем.
3. ↑ ГОСТ 2.721-68 Единая система конструкторской документации. Обозначения условные графические в схемах. Обозначения общего применения.
4. ↑ ГОСТ 2.780-68 Единая система конструкторской документации. Обозначения условные графические. Кондиционеры рабочей среды, емкости гидравлические и пневматические
5. ↑ ГОСТ 2.781-96 Единая система конструкторской документации. Обозначения условные графические. Аппараты гидравлические и пневматические, устройства управления и приборы контрольно-измерительные
6. ↑ ГОСТ 2.782-96 Единая система конструкторской документации. Обозначения условные графические. Машины гидравлические и пневматические.

• Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/ Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др. — 2-е изд., перераб. — М.: Машиностроение, 1982.