Что такое электрическая схема, ветвь, узел, контур.


Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов в рассматриваемой электрической цепи.
Простым языком электрическая схема это упрощенное изображение электрической цепи.
Для отображение электрических компонентов (конденсаторов, резисторов, микросхем и т. д.) в электрических схемах используются их условно графические обозначения.
Для отображения электрических соединений (дорожек, проводов, соединения между радиоэлементами) применяют простую линию соединяющие два условно графических обозначения. Причём все ненужные изгибы дорожек удаляют.
В состав электрической схемы входят: ветвь и условно графические обозначение электрических элементов так же могут входить контур и узел.
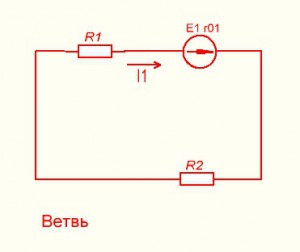

Ветвь – участок цепи состоящий из одного или нескольких элементов вдоль которого ток один и тот же.
Ветви присоединённые к одной паре узлов называются параллельными.
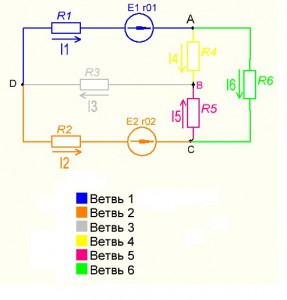

Любой замкнутый путь, проходящий по нескольким ветвям называется контуром. На верхнем рисунке, контурами можно считать ABD; BCD; ABC.
Узел – место соединения трёх и 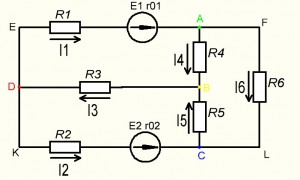
 более ветвей.
более ветвей. - Узел A
- Узел B
- Узел C
- Узел D
Точки К и Е не являются узлами.
8.Электрическая схема, её ветви, узлы, контуры.
Электрическая схема представляет собой графическое изображение электрической цепи. Она показывает, как осуществляется соединение элементов рассматриваемой электрической цепи
Ветвь образуется одним или несколькими последовательно соединенными элементами цепи.
Узел — место соединения трех или большего числа ветвей.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром
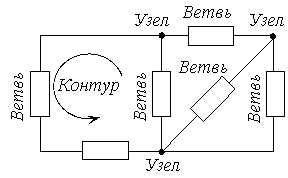
9.Последовательное и параллельное соединение элементов. Устранимый узел.
Под последовательным сопротивлением понимают такое соединение, при котором через все элементы проходит один и тот же ток.
Ветви, присоединенные к 1-ой паре узлов – параллельные ветви. Напряжение на всех параллельных ветвях одинаково.
Узел – место соединения 3-ех и большего числа ветвей.
Устранимый узел – место соединения 2-ух ветвей.
10.Закон Ома для пассивного и активного участка электрической цепи. Применение закона Ома
Закон Ома для пассивного участка электрической цепи.
При
протекании электрического тока через
сопротивление R, напряжение U и ток I на
этом участке связаны между собою согласно
закону Ома: 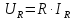 Сопротивление
R
— это коэффициент пропорциональности
между током и напряжением.
Сопротивление
R
— это коэффициент пропорциональности
между током и напряжением.
Закон
Ома можно записать через разность
потенциалов: 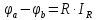
Закон Ома для активного участка цепи между точками а и в имеет вид:

Напряжение на участке электрической цепи Uab и ЭДС берутся со знаком «плюс», если их направление совпадает с направление протекания тока. Напряжение (разность потенциалов) и источник электродвижущей силы берутся со знаком «минус», если их направление не совпадает с направлением протекания тока.
Пример составления уравнения по закону Ома
Рассмотрим пример решения задачи на составления уравнения по закону Ома для участка линейной электрической цепи с двумя источниками ЭДС.
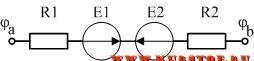
Пусть в данной электрической цепи направление тока будет из точки «a» в точку «b». Напряжение Uab Направляется всегда из первой буквы («a») к последней («b»).
Согласно правилу составления уравнения по закону Ома источник ЭДС E1 берем со знаком «плюс», т.к. его направление (направление стрелочки) совпадает с направлением протекающего тока.
Источник ЭДС E2 берем со знаком «минус», т.к. его направление (направление стрелочки) не совпадает с направлением протекающего тока.
Напряжение Uab или разность потенциалов φa — φb берем со знаком «плюс», т.к. его направление совпадает с направление протекающего тока.
Сопротивление R1 и R1 соединены последовательно. При последовательном соединении сопротивлений их эквивалентное значение равно сумме.
В результате составленное уравнение по закону Ома будет иметь вид:
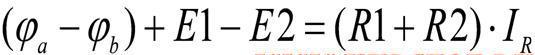
Пусть потенциал в данной задаче потенциал точки «а» равен 10 вольт, потенциал точки «b» = 7 вольт, E1=25 В, E2=17 В, R1=5 Ом, R2=10 Ом. Рассчитаем величину тока:

Полученный ток равен 1 Ампер.
11. Потенциальная диаграмма и ее построение
Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме. 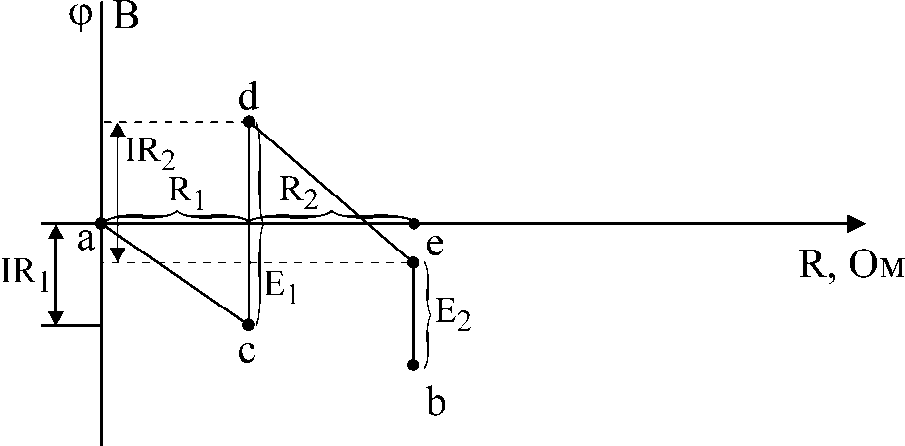
Потенциальная диаграмма построена, начиная с точки a, которая условно принята за начало отсчета. Потенциал aпринят равным нулю.
Точка цепи, потенциал которой условно принимается равным нулю, называется базисной.
Если в условии задачи не оговорено, какая точка является базисной, то можно потенциал любой точки условно приравнивать к нулю. Тогда потенциалы всех остальных точек будут определяться относительно выбранного базиса.
3.Раскройте понятия схема электрической цепи, узел, ветвь, контур. Приведите пример. Укажите количество узлов, ветвей и независимых контуров в электрической цепи (рисунок 1)
Графическое изображение электрической цепи, содержащее условные обозначения ее элементов, называется схемой электрической цепи.
Участок, вдоль которого ток один и тот же, называется ветвью электрической цепи.
Место соединения ветвей называется узлом электрической цепи.
Узел образуется при соединении в одной точке не менее трех ветвей, например на схеме рис. 3.16 к узлу 6 подключены четыре ветви.Всего узлов четыре 1,3,4,6.
Ветви, не содержащие источников электрической энергии, называются пассивными, а ветви, в которые входят источники,—активными.
Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром электрической цепи.
Контур не включающий в себя остальные называется назависимым контуром электрической цепи.На рис. 3.16 таких контуров четыре:1-2-3-1; 1-3-6-1; 3-4-6-3, 4-5-6-4.
На схемах стрелками отмечаются положительные направления ЭДС напряжений и токов. Направление ЭДС может быть указано обозначением полярности зажимов источника: внутри источника ЭДС направлена от отрицательного зажима к положительному (так же как и ток).
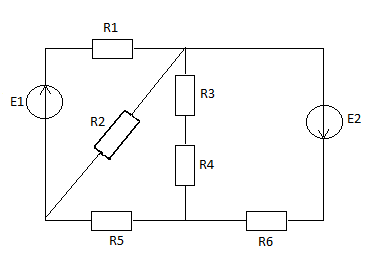
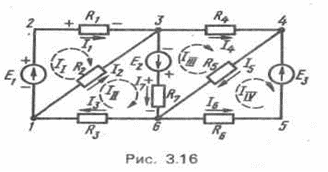
Рисунок 1-Схема электрической цепи
В предложенной схеме (рисунок 1)
количество узлов 3
количество независимых контуров3
4.Сформулируйте первый и второй законы Кирхгофа. Приведите примеры в общем виде.
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлу электрической цепи: алгебраическая сумма токов в ветвях соединённых в один узел равна нулю:
∑ I = 0 , (1)
где I – ток в ветви,А.
В эту сумму токи входят с разными знаками, в зависимости от направления их по отношению к узлу. На основании первого закона Кирхгофа для каждого узла можно составить уравнение токов. Например для схемы 1 уравнения имеют вид:
Узел 1: — I1 – I2 + I3 =0
Узел 3: I1 + I2 – I7 – I4 = 0
Узел 4: I4 – I5 + I6 = 0
Узел 6: — I3 + I7 + I5 – I6 = 0
Этот закон следует из принципа непрерывности тока. Если допустить преобладание в узле токов одного направления, то заряд одного знака должен накапливаться, а потенциал узловой точки непрерывно изменяться, что в реальных цепях не наблюдается.
Пример:
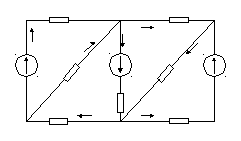
2 R1 3 R4 4
I1 I7 I4
I2 I5
E1 R2 E2 R5 E3
R3 I3 R7 I6 R6
1 6 5
Рисунок 1-Схема электрической цепи
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрических цепей: в контуре электрической цепи алгебраическая сумма ЭДС , входящих в контур,равна алгебраической сумме падений напряжений на пассивных элементах этого контура:
где I – ток в ветви,А;
Е-ЭДС,В;
R-сопротивление, Ом.
При этом положительными считаются токи и ЭДС, направление которых совпадает с направлением обхода.
Согласно этому правилу, запишем уравнения для двух других контуров схемы, представленной на схеме 1:
для 1-2-3-1
I1R1 – I2R2 = E1
для 3-4-6-3
I4R4 + I5R5 – I7R7 = -E2
для 1-3-6-1
I7R7 + I2R2 + I3R3 = E2
для 6-5-4-6
I6R6 + I5R5 = E3
3.Топологические элементы электрической цепи (ветвь, узел, контур). Положительные направления тока, напряжения и эдс.
Ветвь – это участок электрической цепи от одного узла до другого узла. Ветвь обычно содержит один или несколько последовательно соединенных элементов цепи: сопротивления, источники ЭДС или источники тока.
Узел – это участок электрической цепи, содержащий соединения трех или более числа ветвей. Ветви, которые подключены к одной паре узлов называются параллельными. Параллельные ветви или параллельное соединение ветвей всегда находится под общим (одинаковым по величине) напряжением.
Контур — это замкнутый участок электрической цепи. Любой замкнутый путь, проложенный через ветви цепи и есть замкнутый контур
За положительные направления ЭДС источника принимают направления от концов фаз к их началам. Как это обычно делается для источников, фазные токи направляют согласно с ЭДС, а фазные напряжения — в противоположную сторону.
Линейные напряжения направляют следующим образом: напряжение Uab — от а к b, Ubc — отb к с, Uca — от с к а.
Фазные напряжения и токи приемников направляют в одну и ту же сторону, как это обычно делается для приемников. Ток нейтрального провода IN направляют от приемника к источнику
4. Закон Ома.
Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника.
Закон
Ома для полной цепи 
Другая
запись формулы 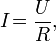
Формулировка: Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи
5.Законы Кирхгофа
Первое правило Кирхгофа:
Алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
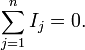
Второе правило Кирхгофа:
Алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС, то суммарное падение напряжений равно нулю:
для постоянных напряжений:
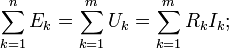
для
переменных напряжений: 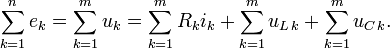
6.Свойства последовательного и параллельного соединения
Свойства последовательного соединения
А)При последовательном соединении проводников сила тока в них одинакова
Б) Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике
В) Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника
Свойства параллельного соединения
А) Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
Б) Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви
В) Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей
7.Расчет цепи постоянного тока с единственным источником
8.Метод контурных токов
Метод контурных токов — метод сокращения размерности системы уравнений, описывающей электрическую цепь
Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми.
Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно.
При составлении уравнений необходимо помнить следующее:
— сумма сопротивлений, входящих в i-й контур;
— сумма сопротивлений, общих для i-го и k-го контуров, причем ;
-члены на главной диагонали всегда пишутся со знаком “+”;
-знак “+” перед остальными членами ставится в случае, если через общее сопротивление i-й и k- й контурные токи проходят в одном направлении, в противном случае ставится знак “-”;
-если i-й и k- й контуры не имеют общих сопротивлений, то ;
-в правой части уравнений записывается алгебраическая сумма ЭДС, входящих в контур: со знаком “+”, если направление ЭДС совпадает с выбранным направлением контурного тока, и “-”, если не совпадает
Топология электрической цепи (Лекция N 2)
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Представленные схемы различны и по форме, и по назначению, но каждая из указанных цепей содержит по 6 ветвей и 4 узла, одинаково соединенных. Таким образом, в смысле геометрии (топологии) соединений ветвей данные схемы идентичны.
Топологические (геометрические) свойства электрической цепи не зависят от типа и свойств элементов, из которых состоит ветвь. Поэтому целесообразно каждую ветвь схемы электрической цепи изобразить отрезком линии. Если каждую ветвь схем на рис. 1 и 2 заменить отрезком линии, получается геометрическая фигура, показанная на рис. 3.
Условное изображение схемы, в котором каждая ветвь заменяется отрезком линии, называется графом электрической цепи. При этом следует помнить, что ветви могут состоять из каких-либо элементов, в свою очередь соединенных различным образом.
Отрезок линии, соответствующий ветви схемы, называется ветвью графа. Граничные точки ветви графа называют узлами графа. Ветвям графа может быть дана определенная ориентация, указанная стрелкой. Граф, у которого все ветви ориентированы, называется ориентированным.
Подграфом графа называется часть графа, т.е. это может быть одна ветвь или один изолированный узел графа, а также любое множество ветвей и узлов, содержащихся в графе.
В теории электрических цепей важное значение имеют следующие подграфы:
1. Путь – это упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются на этом пути только один раз. Например, в схеме на рис. 3 ветви 2-6-5; 4-5; 3-6-4; 1 образуют пути между одной и той же парой узлов 1 и 3. Таким образом, путь – это совокупность ветвей, проходимых непрерывно.
2. Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути. Например, для графа по рис. 3 можно определить контуры, образованные ветвями 2-4-6; 3-5-6; 2-3-5-4. Если между любой парой узлов графа существует связь, то граф называют связным.
3. Дерево – это связный подграф, содержащий все узлы графа, но ни одного контура. Примерами деревьев для графа на рис. 3 могут служить фигуры на рис. 4.
Рис.4
4. Ветви связи (дополнения дерева) – это ветви графа, дополняющие дерево до исходного графа.
Если граф содержит m узлов и n ветвей, то число ветвей любого дерева , а числа ветвей связи графа .
5. Сечение графа – множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых, в частности, может быть отдельным узлом.
Сечение можно наглядно изобразить в виде следа некоторой замкнутой поверхности, рассекающей соответствующие ветви. Примерами таких поверхностей являются для нашего графа на рис. 3 S1 иS2 . При этом получаем соответственно сечения, образованные ветвями 6-4-5 и 6-2-1-5.
С понятием дерева связаны понятия главных контуров и сечений:
- главный контур – контур, состоящий из ветвей дерева и только одной ветви связи;
- главное сечение – сечение, состоящее из ветвей связи и только одной ветви дерева.
Топологические матрицы
Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы: узловую матрицу, контурную матрицу и матрицу сечений.
1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.
Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу АН , принимая, что элемент матрицы (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим
Данная матрица АН записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы АН всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.
Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы АН путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим
Число строк матрицы А равно числу независимых уравнений для узлов , т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.
Первый закон Кирхгофа
Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение
|
(1) |
где — вектор плотности тока; — нормаль к участку dS замкнутой поверхности S.
Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S2 графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать
.
Поскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:
|
(2) |
т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.
При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.
Введем столбцовую матрицу токов ветвей
| I= |
Тогда первый закон Кирхгофа в матричной форме записи имеет вид:
– где O — нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не АН, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.
В качестве примера запишем для схемы на рис. 3
Отсюда для первого узла получаем
,
что и должно иметь место.
2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы Всоответствуют контурам, а столбцы – ветвям схемы.
Элемент bijматрицы В равен 1, если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1, если не совпадает с направлением обхода контура, и 0, если ветвьj не входит в контурi.
Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.
Перейдем теперь ко второму закону Кирхгофа.
Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.
|
(4) |
Просуммируем напряжения на ветвях некоторого контура:
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.
Таким образом, второй закон Кирхгофа математически записывается, как:
|
(5) |
— и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа, т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.
Введем столбцовую матрицу напряжений ветвей
|
U= |
Тогда второй закон Кирхгофа в матричной форме записи имеет вид
В качестве примера для схемы рис. 5 имеем
,
откуда, например, для первого контура получаем
,
что и должно иметь место.
Если ввести столбцовую матрицу узловых потенциалов
| = |
причем потенциал последнего узла , то матрица напряжений ветвей и узловых потенциалов связаны соотношением
| U=AТ |
(7) |
где AТ — транспонированная узловая матрица.
Для определения матрицы В по известной матрице А=АДАС , где АД – подматрица, соответствующая ветвям некоторого дерева, АС— подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-АТС А-1ТД1).
3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа.
Матрица Q , составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Q равно числу независимых сечений.
Элемент qij матрицыQ равен 1, если ветвьвходит в i-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1, если ориентирована противоположно направлению сечения, и 0, если ветвьj не входит в i-е сечение.
В качестве примера составим матрицу Q главных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем
В заключение отметим, что для топологических матриц А, В и Q, составленных для одного и того же графа, выполняются соотношения
которые, в частности, можно использовать для проверки правильности составления этих матриц. Здесь 0 – нулевая матрица порядка .
Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.
Литература
1. Теоретические основы электротехники. Т.1. Основы теории линейных цепей./Под ред. П.А.Ионкина. Учебник для электротехн. вузов. Изд.2-е , перераб. и доп. –М.: Высш. шк., 1976.-544с.
2. Матханов Х.Н. Основы анализа электрических цепей. Линейные цепи.: Учеб. для электротехн. и радиотехн. спец. 3-е изд. переработ. и доп. –М.: Высш. шк., 1990. –400с.
3. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Контрольные вопросы и задачи
- Сформулируйте основные топологические понятия для электрических цепей.
- Что такое узловая матрица?
- Что такое контурная матрица?
- Что такое матрица сечений?
- Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:
- Составить матрицу главных контуров для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5
- Решить задачу 5, используя соотношения (8) и (9).
.
Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв, что ветвям дерева присвоены первые номера.
Ответ:
| B= | |
| Q= |
Ответ:
| B= |
Электрические цепи? Это все о узлах, ветвях и петлях — Новости
Узлы, ветви и петли
Поскольку элементы электрической цепи могут быть взаимосвязаны несколькими способами, нам необходимо понять некоторые основные понятия топологии сети. Чтобы различать схему и сеть, мы можем рассматривать сеть как взаимосвязь элементов или устройств, тогда как схема представляет собой сеть, обеспечивающую один или несколько замкнутых путей.
Электрические цепи? Это все о узлах, ветвях и петлях
Соглашение, когда речь идет о топологии сети, заключается в использовании слова сети, а не схемы . Мы делаем это, хотя слово network и circuit означают одно и то же, когда используются в этом контексте.
В топологии сети мы изучаем свойства, связанные с размещением элементов в сети и геометрической конфигурацией сети. Все дело в элементах схемы, таких как ветви, узлы и циклы.
Ветви //
Ветвь представляет собой один элемент, такой как источник напряжения или резистор. Другими словами, ветвь представляет любой двухтерминальный элемент.
Схема на рисунке 1 имеет пять ветвей, а именно источник напряжения 10 В, источник тока 2А и три резистора.
Рисунок 1 — Узлы, ветви и петли
Узлы //
Узел является точкой соединения между двумя или более ветвями .
Узел обычно обозначается точкой в цепи . Если короткое замыкание (соединительный провод) соединяет два узла, два узла составляют один узел. Схема на рисунке 1 имеет три узла a, b и c .
Обратите внимание, что три точки, которые образуют узел b, соединены идеально проводящими проводами и поэтому составляют единую точку. То же самое относится к четырем точкам, образующим узел c . Мы показываем, что схема на рисунке 1 имеет только три узла путем перерисовки схемы на рисунке 2. Две схемы на рис. 1 и 2 идентичны.
Однако для ясности узлы b и c разложены с совершенными проводниками, как на рис.1.
Рисунок 2 — Трехзвенная схема на рисунке 1 перерисована
Петли //
Цикл — это любой замкнутый путь в цепи .
Цикл представляет собой замкнутый путь, образованный путем запуска на узле, проходящего через набор узлов и возвращающегося к исходному узлу без прохождения через какой-либо узел более одного раза. Цикл называется независимым, если он содержит хотя бы одну ветвь, которая не является частью какого-либо другого независимого цикла. Независимые петли или пути приводят к независимым наборам уравнений.
Можно создать независимый набор петель, где одна из циклов не содержит такой ветви. На рисунке 2 abca с 2Ω резистором независима. Второй контур с резистором 3 Ом и источником тока является независимым. Третий контур может быть с резистором 2 Ом параллельно с резистором 3 Ом. Это создает независимый набор петель.
Сеть с b ветвями, n узлами и l независимыми петлями удовлетворяет фундаментальной теореме топологии сети //
b = l + n — 1
Как показывают следующие два определения, топология схемы имеет большое значение для изучения напряжений и токов в электрической цепи.
Два или несколько элеме
Ветвь и узел электрической цепи
Введение
Подавляющее большинство задач по электротехнике сводится к расчету режимов электрических цепей. В условии задается схема электрической цепи и параметры её элементов (напряжения источников питания, сопротивления резисторов и т. п.). Как правило, требуется определить токи и напряжения на различных элементах цепи.
Электрические цепи, в которых получение электрической энергии в источниках, ее передача и преобразование в приемниках происходят при неизменных по величине во времени токах и напряжениях, принято называть цепями постоянного тока.
Следует заметить что методы решения задач для цепей постоянного тока применимы и для цепей синусоидального тока. Различие только в применяемом математическом аппарате.
Непосредственно перед решением задачи необходимо проанализировать схему электрической цепи и выяснить к какому виду (простая или сложная) относится данная электрическая цепь. Для каждого вида существуют свои варианты и способы решения. Далее выбирают наиболее оптимальный вариант расчета и переходят непосредственно к решению задачи.
Для рассмотрения основных приемов решения подобных задач сначала необходимо определится с ключевыми понятиями, без которых дальнейшее рассмотрение будет просто невозможным.
Элементы электрической цепи
Электрической цепью называют совокупность электрических элементов, соединенных проводниками. Состояние электрической цепи можно описать с помощью понятийнапряжения и тока. Все элементы электрической цепи можно условно разбить на две группы: пассивные элементы (резисторы) и активные элементы (источники электромагнитной энергии).
Резистор — пассивный электрический элемент, характеризуемый величиной, называемой электрическим сопротивлением R. Иногда при расчете цепей удобнее использовать другой величиной, обратной сопротивлению: проводимостью G (1.1).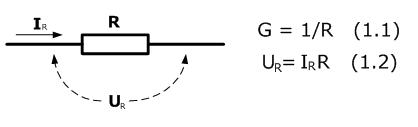
Электрическое сопротивление резистора R, напряжение на его зажимах UR и ток через резистор IR связаны между собой законом Ома (1.2).
Под активными элементами электрической цепи следует понимать любые источники электрической энергии. Различают два вида источников электрической энергии: источники напряжения и источники тока.
Источник напряжения характеризуется двумя параметрами: величиной электродвижущей силы (ЭДС) Е и внутренним сопротивлением R. На схемах отображается в виде последовательного соединения источника ЭДС Е и сопротивления R.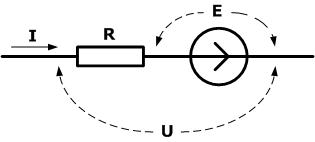
Напряжение на зажимах источника напряжения U отличается от величины ЭДС E на величину падения напряжения на внутреннем сопротивлении источника R. Для случая, когда I = 0 справедливо U = E.
Источник тока также характеризуется двумя параметрами: величиной тока I и внутренним сопротивлением R. На схемах отображается в виде параллельного соединения источника тока со значением I и внутреннего сопротивления R.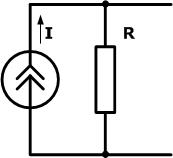
Любой реальный источник электрической энергии можно представить в виде, как источника напряжения, так и источника тока. Иногда при решении задач возникает необходимость трансформировать источник тока в источник напряжения (или наоборот). Эти преобразования легко можно выполнить с помощью формул, приведенных ниже.
Цепи постоянного тока. Элементы цепи, определение.
Цепи постоянного тока это совокупность объектов и устройств, которые создают путь для движения электрического тока. При этом все происходящие электромагнитные процессы описываются с применение понятий об электродвижущей силе электрическом напряжении и токе.
Все объекты и устройства, которые входят в цепь постоянного тока подразделяются на категории. Первая из них это источники тока. Те источники, в которых идет преобразование не электрической энергии в электрическую называются первичными. К ним относятся гальванические элементы аккумуляторы электрогенераторы фотоэлементы. Если же источник преобразует электрическую энергию, то он называется вторичным. К таким источникам можно отнести выпрямители трансформаторы стабилизаторы и преобразователи.
Кроме источников тока существуют потребители. В них идет обратный процесс преобразования энергии. То есть электрическая переходит в другие виды. В частности в тепловую в нагревательных элементах или в электромагнитную в виде излучения.
И все что осталось относиться к вспомогательным элементам цепи постоянного тока. То есть, то, что не является ни источником, ни потребителем энергии. Сюда можно отнести соединительные провода коммутационные разъёмы переключатели измерительные приборы.
Реальные электрические цепи для упрощения их анализа и расчета изображаются в виде электрических схем. В которых реальные объекты и устройства заменяются на графические условные обозначения. Реальные источники тока в таких электрических схемах представляются в виде источника эдс с внутренним сопротивлением. Нагревательные элементы и им подобные изображаются в виде эквивалентного электрического сопротивления.
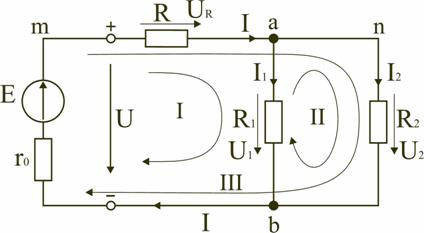
Рисунок 1 — пример электрической схемы
В случае проведения расчетов с использованием электрических схем выделяют некоторые понятия. Например, ветвь электрической цепи это такой участок схемы на котором значение тока неизменно. В такую ветвь может входить от одного до нескольких элементов включённых последовательно.
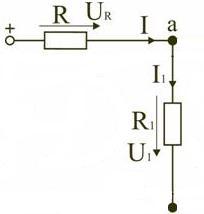
Рисунок 2 — ветвь электрической цепи
Узлом электрической цепи называется та часть цепи, где происходит соединение минимум трех ветвей. На практике их может быть значительно больше. А соединение двух ветвей это будет также одна ветвь без разветвлений, но разбитая на части. И ток в них будет протекать все равно один и тот же. Если две различные ветви соединяют два разных узла, то они называются параллельными.
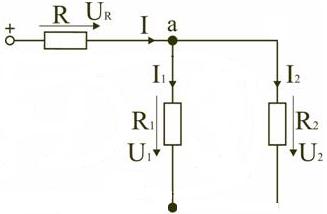
Рисунок 3 — узел электрической цепи
Ток в цепи постоянного тока не может протекать, если она не замкнута. И та часть цепи, которая состоит из нескольких ветвей и при этом она замкнута, называется контуром.
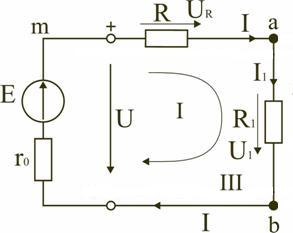
Рисунок 4 — контур электрической цепи
Любая цепь электрического постоянного тока, состоящая из выше перечисленных элементов, может быть отнесена к одному из двух видов цепей. Первая это линейная электрическая цепь. В такой цепи присутствуют только такие элементы параметры, которых не изменяются с изменением тока проходящего через них. В роли такого параметра может выступать сопротивление.
В нелинейных электрических цепях также могут присутствовать линейные элементы. Но отличаются такие цепи наличием одно или более нелинейного элемента. То есть в таком элементе изменяется один из параметров при протекании тока через него. Простейшим нелинейным элементом является лампа накаливания. В холодном состоянии спираль имеет более низкое сопротивление, а при прохождении тока через нее сопротивление увеличивается.
Ветвь и узел электрической цепи
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. В зависимости от особенностей схемы следует применять тот или иной способ расчета электрической цепи. В данном разделе рассмотрим ключевые понятия, которые в дальнейшем будут необходимы для выбора наиболее оптимального и правильного приема решения задач.
Ветвью называется участок электрической цепи, обтекаемый одним и тем же током. Ветвь образуется одним или несколькими последовательно соединенными элементами цепи.
Узел — место соединения трех и более ветвей.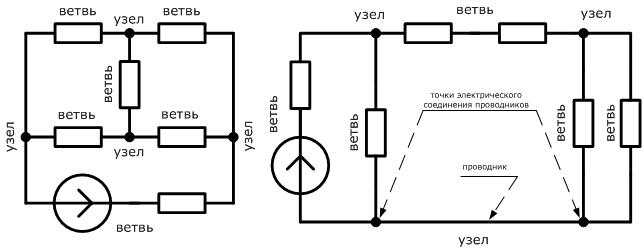
В качестве примера на рисунке изображены схемы двух электрических цепей. Первая из них содержит 6 ветвей и 4 узла. Вторая состоит из 5 ветвей и 3 узлов. В этой схеме обратите внимание на нижний узел. Очень часто допускают ошибку, считая что там 2 узла электрической цепи, мотивируя это наличием на схеме цепи в нижней части 2-х точек соединения проводников. Однако на практике следует считать две и более точки, соединенных между собой проводником, как один узел электрической цепи.
При обходе по соединенным в ветвях цепям можно получить замкнутый контурэлектрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел встречается в данном контуре не более одного раза. Ниже приведена электрическая схема, на которой отмечено несколько произвольно выбранных контуров.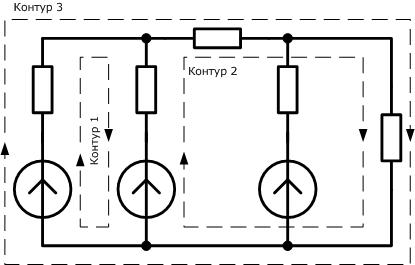
Всего для данной цепи можно выделить 6 замкнутых контуров.
