Расчет токоограничивающего резистора для светодиода
В данной статье речь пойдет о расчете токоограничивающего резистора для светодиода.
Расчет резистора для одного светодиода
Для питания одного светодиода нам понадобится источник питания, например две пальчиковые батарейки по 1,5В каждая. Светодиод возьмем красного цвета, где прямое падение напряжения при рабочем токе 0,02 А (20мА) равно -2 В. Для обычных светодиодов максимально допустимый ток равен 0,02 А. Схема подключения светодиода представлена на рис.1.
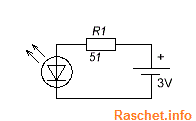
Рис.1 – Схема подключения одного светодиода
Почему я использую термин «прямое падение напряжение», а не напряжение питания. А дело в том, что параметра напряжения питания как такового у светодиодов нет. Вместо этого используется характеристика падения напряжения на светодиоде, что означает величину напряжения на выходе светодиода при прохождении через него номинального тока. Значение напряжения, указанное на упаковке, отражает как раз падение напряжения. Зная эту величину, можно определить оставшееся на светодиоде напряжение. Именно это значение нам нужно применять в расчетах.
Прямое падение напряжение для различных светодиодов в зависимости от длины волны представлено в таблице 1.
Таблица 1 — Характеристики светодиодов
| Цветовая характеристика | Длина волны, нМ | Напряжение, В |
|---|---|---|
| Инфракрасные | от 760 | до 1,9 |
| Красные | 610 — 760 | от 1,6 до 2,03 |
| Оранжевые | 590 — 610 | от 2,03 до 2,1 |
| Желтые | 570 — 590 | от 2,1 до 2,2 |
| Зеленые | 500 — 570 | от 2,2 до 3,5 |
| Синие | 450 — 500 | от 2,5 до 3,7 |
| Фиолетовые | 400 — 450 | 2,8 до 4 |
| Ультрафиолетовые | до 400 | от 3,1 до 4,4 |
| Белые | широкий спектр | от 3 до 3,7 |
Точное значение падения напряжения светодиода, можно узнать на упаковке к данному светодиоду или в справочной литературе.
Сопротивление резистора определяется по формуле:
R = (Uн.п – Uд)/Iд = (3В-2В)/0,02А = 50 Ом.
где:
- Uн.п – напряжение питания, В;
- Uд — прямое падение напряжения на светодиоде, В;
- Iд – рабочий ток светодиода, А.
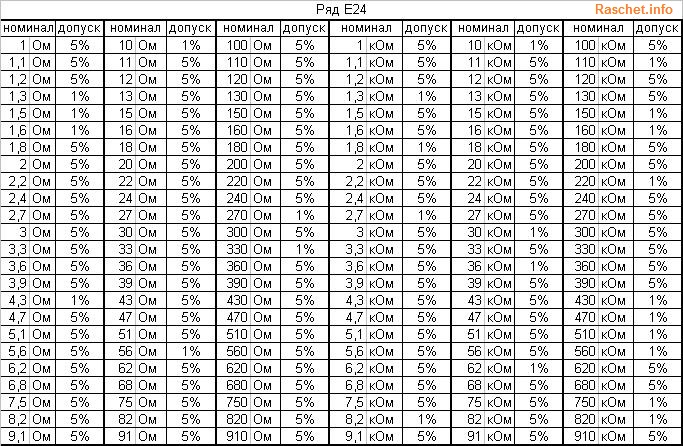
Поскольку такого сопротивления в стандартном ряду нет, выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 51 Ом.
Чтобы гарантировать долгую работу светодиода и исключить ошибку в расчетах, рекомендую при расчетах использовать не максимально допустимый ток – 20 мА, а немного меньше – 15 мА.
Данное уменьшение тока никак не скажется на яркости свечения светодиода для человеческого глаза. Чтобы мы заметили изменение яркости свечения светодиода например в 2 раза, нужно уменьшить ток в 5 раза (согласно закона Вебера — Фехнера).
В результате мы получим, расчетное сопротивление токоограничивающего резистора: R = 50 Ом и мощность рассеивания Р = 0,02 Вт (20мВт).
Расчет резистора при последовательном соединении светодиодов
В случае расчета резистора при последовательном соединении, все светодиоды должны быть одного типа. Схема подключения светодиодов при последовательном соединении представлена на рис.2.
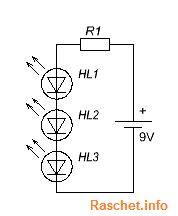
Рис.2 – Схема подключения светодиодов при последовательном соединении
Например мы хотим подключить к блоку питания 9 В, три зеленых светодиода, каждый по 2,4 В, рабочий ток – 20 мА.
Сопротивление резистора определяется по формуле:
R = (Uн.п – Uд1 + Uд2 + Uд3)/Iд = (9В — 2,4В +2,4В +2,4В)/0,02А = 90 Ом.
где:
- Uн.п – напряжение питания, В;
- Uд1…Uд3 — прямое падение напряжения на светодиодах, В;
- Iд – рабочий ток светодиода, А.
Выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 91 Ом.
Расчет резисторов при параллельно – последовательном соединении светодиодов
Часто на практике нам нужно подключить к источнику питания большое количество светодиодов, несколько десятков. Если все светодиоды подключить последовательно через один резистор, то в таком случае напряжения на источнике питания нам не хватит. Решением данной проблемы является параллельно-последовательное соединение светодиодов, как это показано на рис.3.
Исходя из напряжения источника питания, определяется максимальное количество светодиодов, которые можно соединить последовательно.
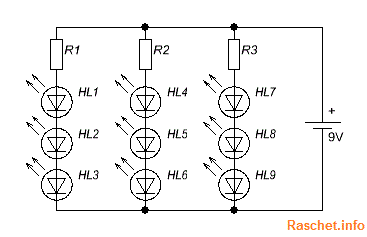
Рис.3 – Схема подключения светодиодов при параллельно — последовательном соединении
Например у нас имеется источник питания 12 В, исходя из напряжения источника питания максимальное количество светодиодов для одной цепи будет равно: 10В/2В = 5 шт, учитывая что на светодиоде (красного цвета) падение напряжения — 2 В.
Почему 10 В, а не 12 В мы взяли, связано это с тем, что на резисторе также будет падение напряжения и мы должны оставить, где то 2 В.
Сопротивление резистора для одной цепи, исходя из рабочего тока светодиодов определяется по формуле:
R = (Uн.п – Uд1 + Uд2 + Uд3+ Uд4+ Uд5)/Iд = (12В — 2В + 2В + 2В + 2В + 2В)/0,02А = 100 Ом.
Выбираем ближайшее сопротивление из номинального ряда Е24 в сторону увеличения — 110 Ом.
Количество таких цепочек из пяти светодиодов параллельно соединенных практически не ограничено!
Расчет резистора при параллельном соединении светодиодов
Данное подключение является не желательным и я его не рекомендую применять на практике. Связано это с тем что, у каждого светодиода присутствует технологическое падение напряжения и даже если все светодиоды из одной упаковке – это не является гарантией, что у них падение напряжение будет одинаково из-за технологии производства.
В результате у одного светодиода, ток будет больше чем у других и если он превысить максимально допустимый ток, он выйдет из строя. Следующий светодиод перегорит быстрее, так как через него уже будет проходить оставшийся ток, распределенный между другими светодиодами и так до тех пор, пока все светодиода не выйдут из строя.
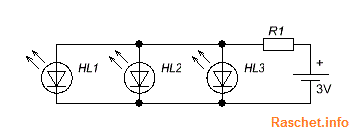
Рис.4 – Схема подключения светодиодов при параллельном соединении
Решить данную проблему можно подключив к каждому светодиоду свой резистор, как это показано на рис.5.
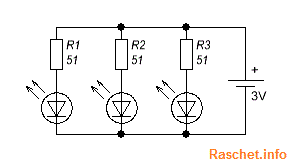
Рис.5 – Схема подключения светодиодов и резисторов при параллельном соединении
Расчет токоограничивающего резистора для переменного резистора
UPD: Вся приведенная ниже статья была написана мной исходя из в корне неправильного понимания смысла параметра «номинальная мощность» для переменного резистора.Я предполагал, что это мощность, которую переменный резистор может рассеять при любом значении его сопротивления. Так вот это не так!
На самом же деле это та мощность, которую резистор безболезненно рассеивает находясь в состоянии максимального сопротивления.
При уменьшении же этого сопротивления мощность (а следовательно и максимально допустимый ток через резистор) падают пропорционально уменьшению его сопротивления!
Power — A pot with a power rating of (say) 0.5W will have a maximum voltage that can exist across the pot before the rating is exceeded. All power ratings are with the entire resistance element in circuit, so maximum dissipation reduces as the resistance is reduced (assuming series or ‘two terminal’ rheostat wiring). Let’s look at the 0.5W pot, and 10k is a good value to start with for explanation.If the maximum dissipation is 0.5W and the resistance is 10k, then the maximum current that may flow through the entire resistance element is determined by…
P = I² * R… therefore
I =√P / R… so I = 7mAIn fact, 7mA is the maximum current that can flow in any part of the resistance element, so if the 10k pot were set to a resistance of 1k, current is still 7mA, and maximum power is now only 50mW, and not the 500mW we had before.
=== ВНИМАНИЕ! ВСЕ, НАПИСАННОЕ НИЖЕ, МАТЕМАТИЧЕСКИ ПРАВИЛЬНО, НО ИСХОДИТ ИЗ НЕВЕРНОЙ ФИЗИЧЕСКОЙ МОДЕЛИ! ДЛЯ РАСЧЕТА НОМИНАЛА ПЕРЕМЕННОГО РЕЗИСТОРА ЭТИ РАСЧЕТЫ ПРИМЕНЯТЬ НЕЛЬЗЯ — ПОЛУЧЕННЫЕ ЗНАЧЕНИЯ СИЛЬНО ЗАВЫШЕНЫ! ===
Вот, казалось бы, куда уж проще задача — при помощи переменного резистора получить простейщий регулируемый «эталон тока» (это я с токовыми шунтами и усилителем на ОУ играюсь). Вроде бы делать нечего, да?
Берем первый попавшийся перменный резистор — например R-0904N-A1K, подсоединяем его к какому-нибудь источнику напряжения в 5 Вольт, начинаем крутить… Естественно, не выкручивать его до нуля соображения все же хватает, ну так мультиметр подключен, показывает ток: 1мА, 5мА, 10мА, 80мА… Блин, сгорел. Чего это он?
А у него оказывается максимальная рассеиваемая мощность — 0.05 Вт. То есть если пропустить через него на 5 Вольтах более 10 мА, то все… Он, в общем-то, хорошо еще держался. Долго.
Упс.
Ну, хорошо. Берем тогда монстроидальный R-24N1-B1K (на фотографии в начале статьи — он).
0.5 Вт рассеиваемой мощности, извините.
Ну и заодно будет нелишне поставить обычный резистор последовательно с переменным в качестве токоограничивающего. Чтобы уж точно не сжечь.
Ну и надо бы посчитать как-нибудь, каким номиналом токоограничивающий резистор ставить. Посчитать бы как-нибудь… А оно как-то не хочет считаться… Какое-то оно все ну совсем нелинейное получается.
Сначала я думал прикинуть номинал в уме. Минут через пятнадцать я понял, что в уме как-то не получается и взял бумажку. Еще через полчаса я тупо глядел на три исписанных листа формата А4 и не мог понять, где я ошибся. Два последовательно подключенных резистора не могут требовать для расчета таких сложных формул!
Начинаем от печки, рисуем схему цепи и вспоминаем закон Ома:
Сила тока в цепи равна:
Мощность, выделяемая всей цепью, Вт:
Падение напряжения на токоограничивающем резисторе R1, Вольт:
Мощность, выделяемая на токоограничивающем резисторе R1, Вт:
Аналогично,
Падение напряжения на переменном резисторе R2, Вольт:
Мощность, выделяемая на переменном резисторе R2, Вт:
Теперь можно загнать эти формулы в Excel и попробовать численно прикинуть, как будут меняться параметры цепи при изменении R2.
Например, возьмем U = 5 Вольт, R1=15 Ом.
А картинка-то получилась… хм… любопытная.
Падения наприяжения на резисторах R1 и R2 ведут себя предсказуемо. По мере того, как растет сопротивление R2 на нем высаживается все большая и большая часть напряжения цепи. Что и понятно — когда R2 близко к нулю имеет значение только сопротивление R1, а при R2 = 150 Ом наличием R1 = 15 Ом (на порядок меньше!) можно смело пренебрегать.
Также предсказуемо падает и ток в цепи, и суммарная мощность, в ней рассеиваемая — напряжение не меняется, суммарное сопротивление растет. Все ожидаемо.
А вот график мощности, рассеиваемой на переменно резисторе W2 имеет весьма необычную форму — мощность, выделяемая на этом резисторе сначала растет, а потом падает.
Если подумать — так и должно быть, ведь пока сопротивление переменного резистора мало он мало влияет на силу тока цепи I (она фактически задается постоянным значением R1) и мощность, выделяемая на R2 растет вместе с ростом R2. А когда R2 велико, то уже R1 не влияет на силу тока, она определяется исключительно значением R2 и падает пропорционально его росту.
Но это я пока картинку не увидел — не осознал.
С практической точки зрения — стоит максимуму выделяемой мощности вылезти за паспортные ограничения резистора, так он и сгорит. Причем не сразу, а когда «неудачно карты лягут» и эта максимальная мощность выделиться.
Теперь при помощи того же Excel-я попробуем прикинуть как ведет себя мощность W2 для разных номиналов токоограничивающего резистора. Опять же при U = 5 Вольт.
Понятно, что чем больше R1, тем ниже максимум мощности, выделяемой на переменном резисторе R2.
И чтобы не превысить ограничения в 0.5 Вт достаточно взять токоограничивающий резистор где-нибудь в 15 Ом — неожиданно небольшое значение…
А теперь попробуем со всем этим взлететь все это посчитать.
Cамо положение максимума мощности нам не слишком интересно, нам важно только то, чтобы этот максимум не превосходил паспортных ограничений по мощности:
С учетом того, что умножаем на него обе части неравенства и раскрываем скобки:
А теперь переносим все на одну сторону и собираем коэффициенты при одинаковых степенях R2:
Мы получили неравенство относительно квадрата переменного сопротивления R2.
Т.к. коэффициент при R2 в квардрате у нас больше нуля, то в левой части мы имеем параболу «рожками вверх». Неравенство будет выполняться при любых значениях R2 если квадратное уравнение в левой части не будет иметь решений. А это, как известно из школьной математики, происходит тогда и только тогда, когда дискрименнант этого квадратного уравнения меньше нуля.
Дискриминант квадратного уровнения
считается по формуле
Подставим в нее коэффициенты нашего уровнения:
Раскроем скобки
… заметим, что в получившимся выражении два члена взаимно уничтожаются и избавимся от них
Квадрат напряжения больше нуля всегда, следовательно, чтобы дискриминант был меньше нуля необходимо:
Итак, для того, чтобы переменный резистор не вышел за пределы своих возможностей, необходимо применять токоограничивающий резистор с сопротивлением не менее, чем:
Для напряжения цепи 5 Вольт и ограничения по рассеиваемой на переменном резисторе мощности в 0.5 Вт получаем, что номинал токоограничивающего резистора R1 должен быть не меньше, чем 25/2= 12.5 Ом.
Однако, сам токоограничивающий резистор также имеет ограничения по рассеиваемой мощности.
Наибольший ток протекает через токоограничивающий резистор в момент, когда переменный резистор выведен в «0» и вся мощность рассеивается на токоограничивающем резисторе.
Исходя из этого (R2=0), получаем ограничение на токоограничивающий резистор
Тут уже для напряжения цепи 5 Вольт и обычного резистора с максимальной рассеиваемой мощностью в 0.25 Вт получаем, что номинал R1 не должен превосходить 100 Ом, что автоматически выполняет и ограничение по мощности на переменном резисторе, однако не позвволяет получить максимальный ток в цепи более 50 мА, что маловато.
Это ограничение можно обойти или взяв в качестве токоограничивающего резистора резистор помощнее или подключив несколько резисторов параллельно…
Токоограничивающий резистор в базе транзистора
Для чего нужен токоограничивающий резистор в базе транзистора? Читали предыдущую статью? Если да, то это очень хорошо, если нет, срочно читайте, иначе не поймёте о чем речь в этой статье.
Для чего ставят резистор в базу
Итак, у некоторых возникли непонятки с резистором, который цепляется к базе транзистора. Вроде бы понятно, что он ограничивает силу тока, но непонятно зачем. Давайте вспомним нашу картинку с предыдущей статьи:
Видите резистор на 500 Ом? Что он там делает и для чего нужен, мы с вами разберем в этой статье.
Итак, у нас есть всеми нами любимый и знакомый транзистор КТ815Б – классика Советского Союза 😉
Вспоминаем его цоколевку (расположение выводов):

Включение транзистора в схему с ОЭ (Общим Эмиттером) будет выглядеть приблизительно вот так:
Как вы видите, в этой схеме мы подключали также лампочку и источник тока к коллектору-эмиттеру.
Откинем пока что лампу и источник Bat2 и просто цепляемся крокодилами от Блока питания на выводы базы и эмиттера:
Плюс от блока питания на базу, а минус на эмиттер.
Теперь давайте будем увеличивать напряжение от нуля и до какого-то значения. Итак, кручу крутилку до 0,6 В и только тогда амперметр на блоке питания показал 10 мА:
Кручу дальше и получаю следующие результаты (слева-направо):
Дальше добавлять напряжение страшновато, так как транзистор становится горячим. Кстати, первый подопытный транзистор скончался, испустив белый дым, под напряжением в 1,5 В. Слишком резко крутанул крутилку).
Давайте построим график по нашим точкам, или как говорится в народе, Вольт амперную характеристику (ВАХ):

Чуток коряво конечно, но смысл уловить можно.
Среди профи-электронщиков этот график называется входной характеристикой биполярного транзистора, при нулевом напряжении на коллектор-эмиттере.
Как вы помните, транзистор можно схематически представить, как два диода, соединенные или анодами, или катодами (кто не помнит, читаем эту статью). В нашем случае транзистор КТ815Б является транзистором NPN, следовательно, его можно представить вот так:
Так что это получается? Мы подавали напряжение на диод? Ну да, все верно)
Так вот, для диода ВАХ будет выглядеть как-то вот так:

Что тут можно увидеть? Подавая напряжение на диод в прямом включении (на анод плюс, на катод – минус), мы видим, что через диод ток начинает течь только тогда, когда напряжение становится больше, чем 0,5 В. Далее подавая напряжение на диод чуточку больше, сила тока через диод возрастает непропорционально. Напряжения добавили чуть-чуть, а сила тока стала в разы больше.
Так как переход база-эмиттер – это что ни на есть самый простой диод, то следовательно, малое изменение напряжения в плюс вызовет большое изменение силы тока. Настолько большое, что транзистор можно сгореть! Для нашего подопечного максимально допустимый постоянный ток базы составляет 0,5 А. Я же выжал 0,7 А, но транзистор за эти пару секунд чуть не вскипел.
Что же это получается? Если напряжение изменится в плюс даже на каких-то десятки Вольт, то транзистор сгорит? Да, все именно так. Но как нам теперь быть? Неужели придется использовать высокостабильный блок питания?
Но выход есть проще некуда, и называется он токоограничивающий резистор.
Давайте проведем два небольших опыта. Для этого к базе цепляем резистор на 10 Ом:
Смотрим теперь на показания блока питания (слево-направо):
Строим график по полученным точкам:

Сравниваем с графиком без резистора:

Обратите внимание на вертикальную шкалу силы тока базы (Iбазы). При одном вольте на графике без резистора базовый ток был уже почти 0,7 А! А с резистором на 10 Ом базовый при 1 В уже был каких-то 0,02 А. Чувствуете разницу?
Почему же так все получилось? Дело в том, что на резисторе “осело” лишнее напряжение. Досконально это схема будет выглядеть вот таким образом:
По цепи, которую я отметил красными проводками, течёт электрический ток. Нагрузкой для электрического тока является резистор и диод транзистора. А так как они соединены последовательно, то вспоминая статью Делитель напряжения можно сказать, что и на диоде транзистора и на резисторе R падает напряжение. А сумма этих напряжений равняется напряжению батареи Bat. В данном случае вместо батареи я использовал блок питания. То есть можно записать, что
UBat = UR + Uбаза-эмиттер
Проверяем, так ли оно на самом деле?
В нашем случае используем тот же самый резистор на 10 Ом. Выставляем на блоке питания напряжение 1 В.
Видим, что сила тока, протекающая по цепи равна 20 мА.
Итак, замеряем падение напряжения на резисторе:
А теперь падение напряжения на базе-эмиттере:
Итого: 0,32 + 0,74 = 1,06 В
0,06 В спишем на погрешность вольтметра блока питания).
Ну как, теперь понятно, почему всё так происходит?
Небольшое лирическое отступление. Так как резистор рассчитан на определенную мощность, нужно таким образом подбирать резистор, чтобы он не колыхнул ярким пламенем. Какая же мощность сейчас в данный момент рассеивается на резисторе? Так как в нашем случае нагрузки подцеплены последовательно (резистор и диод транзистора), сила тока, проходящая через каждую нагрузку везде будет одинаковой. Значит, резистор в данный момент рассеивает мощность, равную
P = IU = 0,02х0,32 = 0,0064 Вт.
Мой резистор рассчитан максимум на 0,25 Вт, значит все гуд. Если на резисторе будет рассеиваться мощность больше, чем 0,25 Вт, то резистор сгорит. Имейте это ввиду, когда будете проектировать свои электронные поделки.
А что будет, если взять резистор еще больше по номиналу? Давайте попробуем. Возьмем резистор на 100 Ом:
И проводим аналогичный опыт. Вот наши показания (слева-направо):
Строим по ним график:

Заключение
Из всего выше сказанного, показанного и написанного делаем простые и не очень выводы:
1) Резистор в базе используется для того, чтобы плавно регулировать силу тока в базе, а также для ограничения силы тока, которая может спалить транзистор. Для чего нам плавно регулировать ток базы, мы с вами еще обсудим.
2) Чем больше номинал резистора, тем больше станет диапазон напряжения для регулировки силы тока в базе, тем самым можно плавнее регулировать этот самый ток.
На рисунке (художник из меня так себе) мы видим резистор, который качается на качелях, прикрепленных к графику входной характеристики транзистора ну и следовательно, чем больше его номинал, тем больше он прогибает график))).

Продолжение——->
<——-Предыдущая статья
Использование резисторов в электронике. » Хабстаб
Резистор можно охарактеризовать тремя параметрами:- сопротивление
- допуск
- мощность
Для того чтобы понять, что такое сопротивление, давайте представим себе трубу, по которой течёт вода. Так как движению воды в трубе ничего не мешает, напор на выходе трубы будет равен напору на входе трубы. Теперь давайте мысленно разрежем трубу на две части и поместим между ними сетку, такую же, как у ситечка, которым мы сеем муку. Желательно ещё представить, что эта сетка обладает некоторой толщиной, но это необязательно. Теперь напор на выходе трубы будет отличаться от напора на входе трубы, а насколько он будет отличаться будет зависеть от размера ячейки сетки.
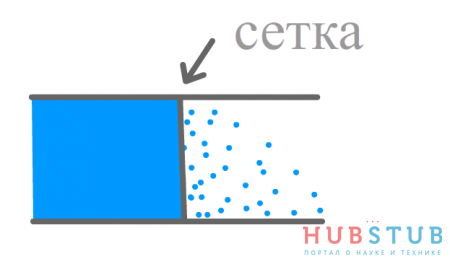
Если провести аналогию с электрической цепью, то ток — это вода, а резистор — сетка, а размер ячейки — сопротивление. Функция сетки — ограничение потока воды, а основное назначение резистора в электрических цепях — ограничение тока.
Допуск показывает насколько реальное сопротивление резистора, может отличается от заявленного. Резистор 100 ом с допуском в 5%, в действительности может обладать сопротивлением от 95 до 105 ом.
Известно что при протекании тока через проводник, последний нагревается, то есть электрическая энергия превращается в тепловую. Мощность резистора определяет какое количество тепла он способен рассеивать. С другой стороны, если записать формулу мощности следующим образом
P = U²/R
P = I²*R
Становится понятно, что мощность определяет максимальный ток, протекающий через резистор или максимальное напряжение, которое может быть к нему приложено. Как правило, более мощные резисторы обладают большими размерами.
Применение резистора.
Токоограничивающий резистор.
Как Вы думаете можно ли подключить светодиод, падение напряжения на котором 2V, к кроне на клеммах которой напряжение 9V?
Конечно можно, надо только ограничить ток текущий через светодиод и в этом нам поможет резистор.
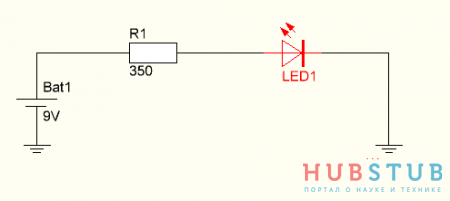
Такой резистор называют токоограничивающим, потому что в данной схеме он предназначен для ограничения тока через светодиод. Его сопротивление легко рассчитать воспользовавшись законом Ома.
I = (Uкроны — Uдиода)/R
А ток через светодиод не должен превышать 20mA, тогда у нас получится следующее
R = (Uкроны — Uдиода)/I
R = (9 –2)/0.02 = 350 ом
Сопротивление можно взять большего номинала, например 470 ом, при этом диод будет не так ярко светиться.
Подтягивающий резистор.
На картинке ниже изображены 4 микросхемы, к двум верхним кнопка подключена без подтягивающего резистора, а к двум нижним с подтягивающим резистором.
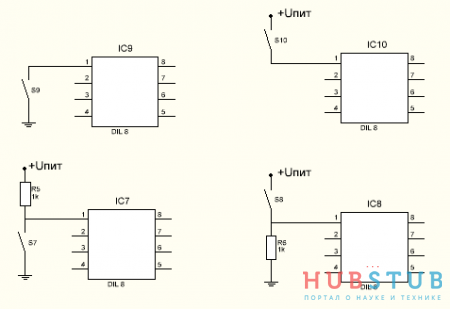
Давайте рассмотрим две верхние микросхемы, когда кнопка нажата, на первом выводе левой микросхемы будет 0V или логический ноль, а на первом выводе правой микросхемы будет напряжение питания или логическая единица. Определить в каком состоянии находится вывод микросхемы когда кнопка не нажата нельзя, вывод просто болтается в воздухе и ловит наводки, которые являются источником ложных срабатываний. Состояние первого вывода нижних микросхем всегда определено, у левой микросхемы, на первом выводе когда кнопка не нажата — логическая единица, когда кнопка нажата — логический ноль, у правой наоборот. Если заменить подтягивающий резистор куском провода, то при нажатии кнопки плюс подключался бы к минусу и ток стремился бы к бесконечности.
Подведём итоги, подтягивающий резистор позволяет избежать состояния неопределённости и ограничивает ток.
Делитель напряжения.
С помощью двух последовательно соединённых резисторов можно разделить напряжение кроны на несколько частей, причём чем больше сопротивление резистора, тем больше на нём падение напряжения.
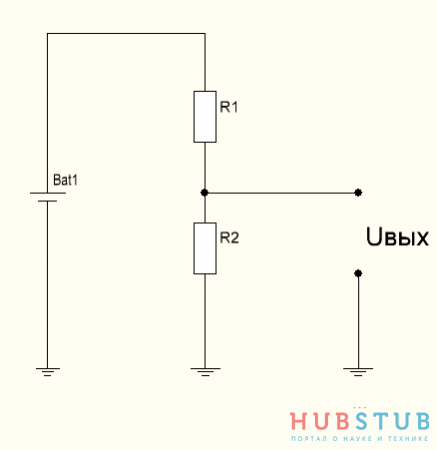
Рассчитать падение напряжения на каждом из резисторов очень просто, для этого надо по закону Ома вычислить ток, протекающий через них и умножить его на сопротивление каждого из резисторов.
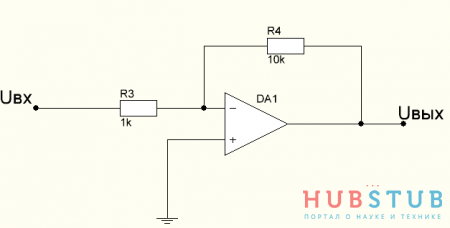
Задание коэффициента усиления операционного усилителя(ОУ)
В данной схеме с помощью резисторов задаётся коэффициент усиления ОУ, но если присмотреться становится понятно, что резисторы на схеме образуют обычный делитель.
Времязадающие цепи.
Резистор совместно с конденсатором образует RC цепочку, с помощью которой можно измерять временный промежутки. Подробнее об этом можно прочитать тут.
Фильтры.
Та же RC цепочка может быть использована как фильтр, высоких или низких частот.
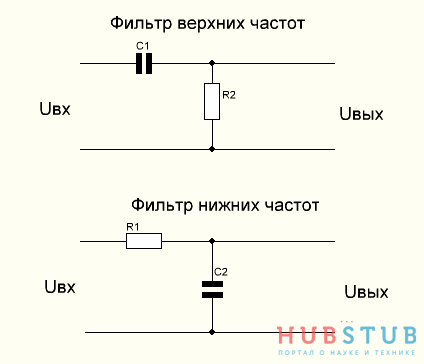
Такие фильтры называют пассивными, в зависимости от номинала резистора и конденсатора они могут без изменения пропускать одни частоты и ослаблять другие.
Кроме обычного резистора о котором писалось выше, существуют резисторы способные изменять своё сопротивление в зависимости от внешних условий. Например, термистор, который изменяет своё сопротивление в зависимости от температуры, или фоторезистор, сопротивление которого зависит от освещения.
Резистор (теория)
Резистор – элемент электрической цепи, применяемый с целью сопротивления электрическому току на отдельном участке цепи.
Сопротивление является главной характеристикой резистора, Ω (Om, Ом) — его единица измерения. Определенная часть тока проходящего через резистор преобразовывается в тепло. Чем больше величина сопротивления, тем большее количество тока рассеивается в тепло.
Общее сопротивление резисторов при последовательном соединении рассчитывается по формуле: Rобщ = R1 + R2. При параллельном соединении резисторов общее сопротивление рассчитывается по данной формуле: Rобщ = R1 * R2 / (R1 + R2). Данным способом можно выходить из ситуации складывающейся при отсутствии резисторов необходимого сопротивления.
Не маловажной характеристикой является мощность резисторов, она показывает максимальную нагрузку, которую в состоянии пропустить через себя резистор. На данный момент выпускают резисторы мощностью 0,125 Watt; 0,25 Watt; 0,5 Watt; 1 Watt; 2 Watt; 5 Вт, но используются в радиолюбительской технике (исключая специализированную) — 0,25 Watt; 0,5 Watt; 1 Watt. На главном изображении поста приведен внешний вид резисторов разной мощности. Нагрузку, действующую на резистор можно посчитать по формуле: P = I2 *R = I * U = U2 / R, где R – сопротивление, U – напряжение, а I – сила тока.
При превышении максимально допустимой нагрузки, резистор будет нагреваться, и вносить помехи в стоящие рядом радио детали (подверженные тепловым изменениям), а при большом превышении нагрузки резистор перегорает (в буквальном смысле этого слова).
Благодаря закону Ома, зная величину силы тока (I) и напряжения (U тоже, что и V) можно определить сопротивление (R) по следующей формуле: R = U / I.
На практике резисторы выполняют три назначения и служат:
— делителями напряжения;
— токоограничивающими резисторами;
— подтягивающими и стягивающими резисторами.
Делитель напряжения необходим для того, чтобы получать всего его часть, например из 12v получить 9v. Про делители напряжения будет отдельная большая статья с примерами, по окончанию ее написания ссылку размещу в комментариях к данному посту.
Токоограничивающий резистор применяют в случае, когда какая-либо деталь не рассчитана на работу при определенно высоком уровне тока, и его необходимо уменьшить. В данной ситуации резистор устанавливается последовательно между положительным контактом источника питания участка цепи (детали) и самим участком цепи (деталью) на котором уровень тока необходимо уменьшить.
Подтягивающий и стягивающий резистор необходим только для работы с логическими компонентами, для которых важно присутствие нуля и единицы на контакте (отсутствие или присутствие напряжения). Без подтягивающих и стягивающих резисторов возможны сбои в работе системы из-за неверного истолкования шумов, улавливаемых контактами логики, как присутствие нуля или единицы.
Рассмотрим примеры с использованием микроконтроллера и кнопки. Один контакт кнопки подключен к входу микроконтроллера, а другой к источнику сигнала.
Для гарантирования правильного считывания положительного сигнала используют стягивающий резистор, установленный одним концом в промежуток между кнопкой и контактом микроконтроллера, а другим соединенным с землей (GND). В этом случае все возможные шумы, способные дать неверный сигнал на микроконтроллер, будут уходить в землю. В роли стягивающего резистора применяют сопротивления более 10 kOm, чтобы при нажатии кнопки не происходило короткое замыкание. Когда кнопка нажата, цепь замыкается, ток из-за большого сопротивления резистора не уходит весь в землю и сигнал поступает на контакт микроконтроллера.
Подтягивающий резистор подобен токоограничивающему и аналогичен стягивающему. Он поддерживает на контакте микроконтроллера логическую единицу до тех пор, пока цепь разомкнута. Сопротивление для подтягивающего резистора необходимо брать также не менее 10 kOm, это предотвращает короткое замыкание и сводит к минимуму потери энергии при нажатии кнопки.
Разновидность резисторов, применяемая в радиоаппаратуре: варисторы – сопротивление меняется от приложенного напряжения; фоторезисторы – от освещения, терморезисторы – от температуры, магниторезисторы – от величины магнитного поля, тензорезисторы – от деформации корпуса резистора.
Калькулятор расчета величины сопротивления резистора по цветам (цветовой маркировке) можно найти ЗДЕСЬ.
Резистор в цепи затвора или как делать правильно / Habr
Всем доброго времени суток!
Эта небольшая статья возможно станет шпаргалкой для начинающих разработчиков, которые хотят проектировать надежные и эффективные схемы управления силовыми полупроводниковыми ключами, обновит и освежит старые знания опытных специалистов или может хотя бы где-то поцарапает закрома памяти читателей.
Любому из этих случаев я буду очень рад.
В этой заметке я попробую описать наиболее распространенные вопросы выбора затворных резисторов для силовых электронных устройств. Она базируется на знаниях, почерпнутых мной из разной литературы, апноутов от TOSHIBA, Infineon, Texas Instruments а также из скромной практики. Стоит заметить, что эта информация не дает прямо универсальных рекомендаций для каждого силового ключа. Тем не менее, можно проанализировать какие предположения могут быть важны и какое влияние они могут оказать на выбор резисторов затвора для дискретных силовых транзисторов, а также для силовых модулей.
Основы
Затворный резистор расположен в цепи между драйвером силового транзистора и затвором самого транзистора, как показано на изображении в шапке статьи.
Открыт или закрыт полевой ключ (IGBT/MOSFET) зависит от приложенного к затвору напряжения. Изменение этого напряжения заряжает или разряжает затворные емкости силового устройства, которые состоят из емкостей затвора-коллектора и затвора-эмиттера и небольшой емкости самого затвора. Заряд входных емкостей ключа включит его (ток ), а разряд выключит (ток ).
Резистор в данной цепи ограничивает ток заряда/разряда входных емкостей, помимо этого, правильно подобранный резистор не даст ключу самопроизвольно открываться, что иногда может случиться, из-за быстрого изменения напряжения на силовых выводах ключа например, такое может случиться, когда в полумостовой топологии соседний ключ открывается. В таком случае емкость перезаряжается и ток, протекающий через затворный резистор вызывает на нем падение напряжения, которое и может открыть ключ. К тому же порог открывания ключа часто сильно опускается при росте температуры кристалла полупроводника.
Что нужно знать и как выбрать “правильный” резистор
1. Максимальный ток заряда/разряда выхода драйвера
Любая микросхема драйвера имеет такой параметр, как максимальный выходной ток. Если ток затвора при открытии/закрытии ключа превысит значение максимального выходного тока, то драйвер может выйти из строя, поэтому, в данном случае, затворный резистор ограничит выходной ток драйвера.
Можно составить эквивалентную модель цепи, по которой и рассчитать необходимое значение резистора:
Следуя несложным умозаключениям, можем получить формулы для расчета тока драйвера, и подобрать резистор затвора таким, чтобы не превысить максимально допустимые параметры драйвера:
2. Рассеиваемая мощность
Также одна из важных функций затворного резистора — рассеивать мощность выходного каскада микросхемы драйвера. В соответствии с моделью выше, рассеиваемую мощность можно посчитать с помощью следующих формул:
Тут — заряд затвора ключа, а — частота коммутации.
После расчета и подбора резистора важно соблюдать следующее условие:где — собственное потребление драйвера.
Тут еще есть небольшое примечание, в большинстве даташитов на ключи указывают заряд затвора при определенных условиях, например при напряжении управления затвором +15В…-15В, если же в Вашей схеме другое напряжение управления, например +15В…0В, или же +15…-8В, то достаточно точно определить заряд затвора помогут следующие соотношения:
3. Скорость включения и электромагнитная совместимость
Давайте рассмотрим потери на переключение, как функцию от сопротивления затворного резистора. Я возьму ключ, который я недавно использовал в своем небольшом проекте — IKW40N120 от любимых Infineon:
Как можно заметить, при увеличении сопротивления затвора, скорость переключения уменьшается и потери на переключения растут. Соответственно это повлияет на эффективность системы в целом. Напротив, если применять меньшее сопротивление затвора, переключение станет более быстрым и потери уменьшаться, но при этом шум, вызванный быстрым нарастанием тока и напряжения, будет увеличиваться, что может быть критично, когда нужно отвечать требованиям электромагнитной совместимости поэтому значение сопротивления затвора нужно выбирать очень аккуратно.
4. То самое “паразитное” включение
В начале, когда я писал о функциях затворного резистора, я упоминал о возможности ключа самопроизвольно включиться. Чтобы такого не случилось, можно рассчитать напряжение, которое может появиться на затворе транзистора, посмотрим на изображение ниже и запишем две небольшие формулы:
И не стоит забывать, что напряжение открытия ключа сильно зависит от температуры кристалла, и это тоже нужно учитывать.Заключение
Теперь у нас есть формулы для оптимального (в какой-то степени) подбора с первого взгляда такого простого элемента силовой схемы, как затворный резистор.
Вполне возможно вы не нашли тут ничего нового, но я надеюсь, что хоть кому-то эта заметка окажется полезной.
Также для расширения кругозора в том числе в области управлении силовыми ключами очень советую выделять часик-два в неделю на прочтение всяких статей и апноутов от именитых производителей силовой электроники, в особенности о применении микросхем драйверов. Уверен, найдёте там очень много интересностей. Для старта, и чтобы углубится в рассмотренную тему предлагаю вот эту.
Спасибо за прочтение!
Резистор
Как по конструкции, так и по своим электрическим параметрам резисторы весьма разнообразны. Существуют миниатюрные (и малой мощности), а также больших размеров (и высокой мощности) резисторы.
Радиолюбители чаще всего используют миниатюрные резисторы, именно такие, как правило, применяются в транзисторных схемах. Единицей сопротивления резистора является Ом. Большие сопротивления измеряются килоомами (КОм) и мегаомами (МОм):
1 КОм = 1000 Ом
1 МОм = 1000 КОм = 1000000 Ом
При изучении обычно пользуются резисторами сопротивлением от 20 Ом до 2 МОм, т.е 2000000 Ом.
Кроме сопротивления каждый резистор характеризуется определенной номинальной мощностью (в ваттах), на которую он рассчитан. Миниатюрные резисторы бывают мощностью 0.1 Вт, 0.25 Вт и 0.5 Вт. Обозначение резистора — 220 Ом / 0.25 Вт, означает, что данный резистор имеет сопротивление 220 Ом и мощность 0.25 Вт. Резистор 220 Ом / 0.5 Вт имеет аналогичное сопротивление, от предыдущего он отличается большими размерами. На каждом резисторе указывается величина его сопротивления и мощности.
Иногда бывают трудности с подбором требуемого резистора. Допускается применение резисторов с 20% отклонением от номинальных требуемых величин, т.е. вместо резистора сопротивлением 1000 Ом, необходимого в данной системе, можно поставить любой резистор сопротивлением в пределах от 800 до 1200 Ом. Еще проще дело обстоит с подбором мощности, так как всегда можно использовать резистор, рассчитанный на большую мощность.
Последовательное соединение резисторов. Например, в случае отсутствия требуемого резистора 1000 Ом / 0.1 Вт может быть использован резистор 1000 Ом / 0.25 Вт или даже 1000 Ом / 0.5 Вт. Правда они будут больших размеров, а это не всегда желательно.
В некоторых случаях можно воспользоваться последовательным соединением резисторов. Допустим, под рукой нет резистора сопротивлением 2000 Ом, вместо него можно взять два резистора по 1000 Ом каждый и последовательно соединить их.
Закон ОМА
Закон Ома позволяет на заданном участке цепи определить одну из величин: силу тока I, напряжение U, сопротивление R, если известны две остальные:
Расчитаем силу тока, проходящего через резистор R1 и, соответственно, затем через лампу L1. Для простоты будем предполагать, что сама лампа обладает нулевым собственным сопротивлением.
Аналогично, если бы у нас был источник питания на 5 В и лампа, которая по документации должна работать при токе 20 мА, нам нужно бы было выбрать резистор подходящего номинала.
В данном случае, разница в 10 Ом между идеальным номиналом и имеющимся не играет большого значения: можно смело брать стандартный номинал — 240 или 220 Ом.
Аналогично, мы могли бы расчитать требуемое напряжение, если бы оно было не известно, а на руках были значения сопротивления и желаемая сила тока.
Соединение резисторов
При последовательном соединении резисторов, их сопротивление суммируется:
При параллельном соединении, итоговое сопротивление расчитывается по формуле:
Если резистора всего два, то:
В частном случае двух одинаковых резисторов, итоговое сопротивление при параллельном соединении равно половине сопротивления каждого из них.
Таким образом можно получать новые номиналы из имеющихся в наличии.
Применение на практике
Среди ролей, которые может выполнять резистор в схеме можно выделить следующие:
- Токоограничивающий резистор (current-limiting resistor)
- Стягивающий, подтягивающий резистор (pull-down / pull-up resistor)
- Делитель напряжения (voltage divider)
Токоограничивающий резистор
Пример, на котором рассматривался Закон Ома представляет собой также пример токоограничевающего резистора: у нас есть компонент, который расчитан на работу при определённом токе — резистор снижает силу тока до нужного уровня.
В случае с Ардуино следует ограничивать ток, поступающий с выходных контактов (output pins). Напряжение, в состоянии, когда контакт включен (high) составляет 5 В. Исходя из документации, ток не должен превышать 40 мА. Таким образом, чтобы безопасно увести ток с контакта в землю понадобится резистор номиналом R = U / I = 5 В / 0.04 А = 125 Ом или более.
Смягчающие и подтягивающие резисторы
Стягивающие (pull-down) и подтягивающие (pull-up) резисторы используются в схемах рядом со входными контактами логических компонентов, которым важен только факт: подаётся ноль вольт (логический ноль) или не ноль (логическая единица). Примером являются цифровые входы Ардуино. Резисторы нужны, чтобы не оставить вход в «подвешенном» состоянии. Возьмём такую схему
Мы хотим, чтобы когда кнопка не нажата (цепь разомкнута), вход фиксировал отсутствие напряжения. Но в данном случае вход находится в «никаком» состоянии. Он может срабатывать и не срабатывать хаотично, непредсказуемым образом. Причина тому — шумы, образующиеся вокруг: провода действуют как маленькие антенны и производят электричество из электромагнитных волн среды. Чтобы гарантировать отсутствие напряжения при разомкнутой цепи, рядом с входом ставится стягивающий резистор:
Теперь нежелательный ток будет уходить через резистор в землю. Для стягивания используются резисторы больших сопротивлений (10 кОм и более). В моменты, когда цепь замкнута, большое сопротивление резистора не даёт большей части тока идти в землю: сигнал пойдёт к входному контакту. Если бы сопротивление резистора было мало (единицы Ом), при замкнутой цепи произошло бы короткое замыкание.
Аналогично, подтягивающий резистор удерживает вход в состоянии логической единицы, пока внешняя цепь разомкнута:
То же самое: используются резисторы больших номиналов (10 кОм и более), чтобы минимизировать потери энергии при замкнутой цепи и предотвратить короткое замыкание при разомкнутой.
Делитель напряжения
Делитель напряжения (voltage divider) используется для того, чтобы получить из исходного напряжения лишь его часть. Например, из 9 В получить 5. Он подробно описан в отдельной статье.
Мощность резисторов
Резисторы помимо сопротивления обладают ещё характеристикой мощности. Она определяет нагрузку, которую способен выдержать резистор. Среди обычных керамических резисторов наиболее распространены показатели 0.25 Вт, 0.5 Вт и 1 Вт. Для расчёта нагрузки, действующей на резистор, используйте формулу:
При превышении допустимой нагрузки, резистор будет греться и его срок службы может сильно сократиться. При сильном превышении — резистор может начать плавиться и вызвать воспламенение. Будьте осторожны!
