Последовательное и параллельное соединение — Википедия

Материал из Википедии — свободной энциклопедии

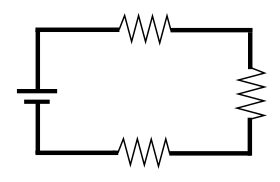Последовательное соединение проводников. 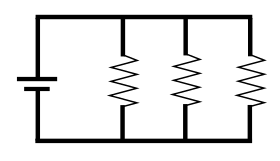Параллельное соединение проводников.

Последовательное и параллельное соединения в электротехнике — два основных способа соединения элементов электрической цепи. При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла. При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами, если это не противоречит условию.

При последовательном соединении проводников сила тока во всех проводниках одинакова. При этом общее напряжение в цепи равно сумме напряжений на концах каждого из проводников.

При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов. При этом величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включённых проводников.

При последовательном соединении проводников сила тока в любых частях цепи одна и та же: I=I1=I2=⋯=In{\displaystyle I\mathrm {=} I_{1}=I_{2}=\cdots =I_{n}} (так как сила тока определяется количеством электронов, проходящих через поперечное сечение проводника, и если в цепи нет узлов, то все электроны в ней будут течь по одному проводнику).

Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника питания, равно сумме напряжений на отдельных участках цепи: U=U1+U2+⋯+Un{\displaystyle U\mathrm {=} U_{1}+U_{2}+\cdots +U_{n}}.

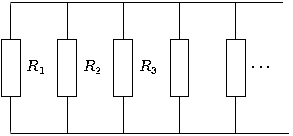
Резисторы[править | править код]

R=R1+R2+⋯+Rn{\displaystyle R=R_{1}+R_{2}+\cdots +R_{n}}

Катушка индуктивности[править | править код]

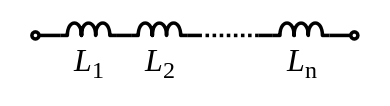
L=L1+L2+⋯+Ln{\displaystyle L=L_{1}+L_{2}+\cdots +L_{n}}

Электрический конденсатор[править | править код]

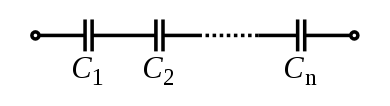
1C=1C1+1C2+⋯+1Cn{\displaystyle {\frac {1}{C}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}}.

Мемристоры[править | править код]

M=M1+M2+⋯+Mn{\displaystyle M=M_{1}+M_{2}+\cdots +M_{n}}

Выключатели[править | править код]

Цепь замкнута, когда замкнуты все выключатели. Цепь разомкнута, когда разомкнут хотя бы один выключатель. (См.также Логическая операция И).

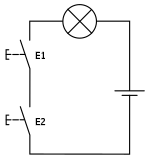
Сила тока в неразветвлённой части цепи равна сумме сил тока в отдельных параллельно соединённых проводниках: I=I1+I2+⋯+In{\displaystyle I\mathrm {=} I_{1}+I_{2}+\cdots +I_{n}}

Напряжение на участках цепи АВ и на концах всех параллельно соединённых проводников одно и то же: U=U1=U2=⋯=Un{\displaystyle U\mathrm {=} U_{1}=U_{2}=\cdots =U_{n}}

Резисторы[править | править код]

При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость 1R{\displaystyle {\frac {1}{R}}} складывается из проводимостей каждого резистора 1Ri{\displaystyle {\frac {1}{R_{i}}}})

Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включённые между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.

Доказательство

Для двух параллельно соединённых резисторов их общее сопротивление равно: R=R1R2R1+R2{\displaystyle R={\frac {R_{1}R_{2}}{R_{1}+R_{2}}}}.

Если R1=R2=R3=…=Rn{\displaystyle R_{1}=R_{2}=R_{3}=…=R_{n}}, то общее сопротивление равно: R=R1n{\displaystyle R={\frac {R_{1}}{n}}}.

При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.

Катушка индуктивности[править | править код]

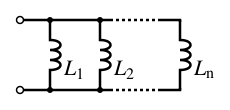
1Ltotal=1L1+1L2+⋯+1Ln{\displaystyle {\frac {1}{L_{\mathrm {total} }}}={\frac {1}{L_{1}}}+{\frac {1}{L_{2}}}+\cdots +{\frac {1}{L_{n}}}}

Электрический конденсатор[править | править код]

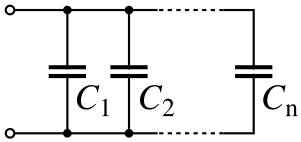
Ctotal=C1+C2+⋯+Cn{\displaystyle C_{\mathrm {total} }=C_{1}+C_{2}+\cdots +C_{n}}.

Мемристоры[править | править код]

Mtotal=M1‖M2‖⋯‖Mn=(M1−1+M2−1+⋯+Mn−1)−1{\displaystyle M_{total}=M_{1}\|M_{2}\|\cdots \|M_{n}=\left(M_{1}^{-1}+M_{2}^{-1}+\cdots +M_{n}^{-1}\right)^{-1}}

Выключатели[править | править код]

Цепь замкнута, когда замкнут хотя бы один из выключателей.

• Батареи гальванических элементов или аккумуляторов, в которых отдельные химические источники тока соединены последовательно (для увеличения напряжения) или параллельно (для увеличения тока).
• Регулировка мощности электрического устройства, состоящего из нескольких одинаковых потребителей электроэнергии, путём их переключения с параллельного на последовательное соединение. Таким способом регулируется мощность конфорки электрической плиты, состоящей из нескольких спиралей; мощность (скорость движения) электровоза, имеющего несколько тяговых двигателей.
• Делитель напряжения
• Балласт
• Шунт

• Перышкин А. В. Учебник для общеобразовательных учреждений 10 класс. М.: 2011. С.121
• Перышкин А. В. Учебник для общеобразовательных учреждений 8 класс № 42

11. Последовательное, параллельное и смешанное соединения резисторов.

Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.

Последовательное соединение. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с

началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I.

Последовательное соединение приемников поясняет рис. 19,а. Заменяя лампы резисторами с сопротивлениямиR₁, R₂ и R₃ получим схему, показанную на рис. 19,б.Если принять, что в источнике R₀ = 0, то для трех последова-тельно соединенных резисторов согласно второму Кирхгофа можно написать:

E = IR₁ +IR₂ +IR₃ = I( R₁+ R₂+ R₃ ) = IR_общ ;

где: R_общ = R₁+ R₂+ R₃

Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.

Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.

Соединять последовательно целесообразно только приемники с одинаковыми сопротивлениями. В противном случае приложенное напряжение источника электрической энергии распределяется между ними неравномерно и отдельные приемники могут оказаться под недопустимо высоким для них напряжением.

При последовательном соединении приемников изменение сопротивления одного из них влечет за собой изменение напряжения на других связанных с ним приемниках. При обрыве электрической цепи в одном из приемников в остальных прекращается ток.

При параллельном соединении приемники включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 20,а). Заменяя лампы резисторами с сопро-тивлениями R₁, R₂ и R₃, получим схему, показанную на рис. 20,б.

При параллельном соединении ко всем резисторам приложено одинаковое напряжениеU. Поэтому согласно закону Ома:

I₁ = U/R₁, I₂ =U/R₂ , I₃ = U/R₃

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I=I₁+I₂ +I₃ или

I= U/R₁ + U/R₂ + U/R₃ = U (1/ R₁ + 1/ R₂+ 1/ R₃) = U/R_экв

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/ R_экв= 1/ R₁ + 1/ R₂+ 1/ R₃

При увеличении числа параллельно включаемых резисторов результирующее сопротивление уменьшается.

При параллельном соединении приемников все они находятся под одним и тем же напряжением и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными.

Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом

преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую.

Виды соединения проводников

При решении задач принято преобразовывать схему, так, чтобы она была как можно проще. Для этого применяют эквивалентные преобразования. Эквивалентными называют такие преобразования части схемы электрической цепи, при которых токи и напряжения в не преобразованной её части остаются неизменными.

Существует четыре основных вида соединения проводников: последовательное, параллельное, смешанное и мостовое.

Последовательное соединение

Последовательное соединение – это такое соединение, при котором сила тока на всем участке цепи одинакова. Ярким примером последовательного соединения является старая елочная гирлянда. Там лампочки подключены последовательно, друг за другом. Теперь представьте, одна лампочка перегорает, цепь нарушена и остальные лампочки гаснут. Выход из строя одного элемента, ведет за собой отключение всех остальных, это является существенным недостатком последовательного соединения.

При последовательном соединении сопротивления элементов суммируются. 

Параллельное соединение

Параллельное соединение – это соединение, при котором напряжение на концах участка цепи одинаково. Параллельное соединение наиболее распространено, в основном потому, что все элементы находятся под одним напряжением, сила тока распределена по-разному и при выходе одного из элементов все остальные продолжают свою работу.

При параллельном соединении эквивалентное сопротивление находится как:

В случае двух параллельно соединенных резисторов

В случае трех параллельно подключенных резисторов:

Смешанное соединение

Смешанное соединение – соединение, которое является совокупностью последовательных и параллельных соединений. Для нахождения эквивалентного сопротивления нужно, “свернуть” схему поочередным преобразованием параллельных и последовательных участков цепи.

Сначала найдем эквивалентное сопротивление для параллельного участка цепи, а затем прибавим к нему оставшееся сопротивление R₃. Следует понимать, что после преобразования эквивалентное сопротивление R₁R₂ и резистор R₃, соединены последовательно.

 

Итак, остается самое интересное и самое сложное соединение проводников.

Мостовая схема

Мостовая схема соединения представлена на рисунке ниже.

Для того чтобы свернуть мостовую схему, один из треугольников моста, заменяют эквивалентной звездой.

И находят сопротивления R₁, R₂ и R₃. 

Затем находят общее эквивалентное сопротивление, учитывая, что резисторы R₃,R₄ и R₅,R₂ соединены между друг другом последовательно, а в парах параллельно. 

На этом всё! Примеры расчета сопротивления цепей тут.

Просмотров: 18523

Электротехника часть 4. Соединение элементов цепи

Всем доброго времени суток. В прошлой статье я рассмотрел закон Ома, применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса токов, называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и сопротивлениями.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Последовательное соединение приемников энергии

Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии

Пример последовательного подключения приемников энергии.

В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с напряжением U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления

Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.

Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями

где R – эквивалентное последовательное сопротивление.

Применение последовательного соединения

Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр

Делитель напряжения (слева) и потенциометр (справа).

В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.

Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.

Параллельное соединение приемников энергии

Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже

Пример параллельного соединения приемников энергии.

Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви

Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений

Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.

Смешанное соединение приемников энергии

Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии

Пример смешанного соединения приемников энергии.

В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид

В результате получили цепь из двух последовательных приемников энергии R₁₂R₃₄₅ эквивалентное сопротивление и ток, протекающий через них, составит

Тогда падение напряжения по участкам составит

Тогда токи, протекающие через каждый приемник энергии, составят

Первый закон Кирхгофа

Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.

Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением

где ∑ — обозначает алгебраическую сумму.

Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа

Изображение первого закона Кирхгофа.

На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид

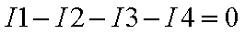
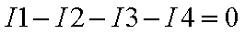
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.

Второй закон Кирхгофа

Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением

В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур

Схема, иллюстрирующая второй закон Кирхгофа.

Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид

Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Последовательное соединение резисторов

Это такое соединение, при котором все элементы идут один за одним без разветвлений.

Свойства последовательного соединения

1. Ток во всех резисторах одинаков- I₁ = I₂ = I₃;

2. Общее напряжение цепи равно сумме напряжений на всех резисторах- U=U₁ + U₂ + U₃;

3.Сопротивление по отношению к входным зажимам называется входным сопротивлением и равно сумме сопротивлений участков — R_вх= R₁ + R₂ + R₃;

4. Чем больше сопротивление участка, тем больше на нём падает напряжение-.

Параллельное соединение резисторов

Это такое соединение, при котором все начала элементов соединяются в одну точку, а все концы в другую и к этим точкам подводится напряжение.

Свойства параллельного соединения резистора:

1. Общее напряжение цепи равно напряжению на каждом участке-

U = U₁ = U₂ = U₃

2. Общий ток цепи равен сумме токов на всех участках- I = I₁ + I₂ + I₃

3. Чтобы найти входное сопротивление, рассчитывают вначале величину обратную входному сопротивлению

— проводимость (G)

Общая проводимость цепи равна сумме проводимостей на каждом участке.

G = G₁ + G₂ + G₃

4.Чем больше сопротивление участка, тем меньше ток, протекающий на нем.

При параллельном соединении двух резисторов формулу входного сопротивления можно преобразовать

1.

2. Если известен общий ток, то можно найти ток ветви, умножив общий ток на сопротивление противоположной ветви и разделить на сумму сопротивлений ;.

Тестовые задания:

Задание		Варианты ответов
1.Являются ли при последовательном соединении резисторов напряжения участков пропорционально сопротивлениям этих участков.		Да; Нет.
2.Являются ли при параллельном соединении резисторов токи ветвей пропорциональны сопротивлениям этих ветвей.		Да; Нет.
3.Укажите по какому из приведенных математических выражений нельзя рассчитать входное сопротивление двух параллельно соединенных резисторов.	а) ; б); в) ; г)

Смешанное соединение резисторов

Пример решения задач

Дано:

U = 60 В

R₁ = 7 Ом

R₂ = 12 Ом

R₃ = 4 Ом

Найти: I₁; I₂; I₃ = ?

РезисторыR2 и R3 параллельны между собой, и их общее сопротивление R_2-3 последовательно с R₁.

R_вх = R₁ + R_{2 — 3}

R_вх =R₁+R_2∙3= 7 + 3 = 10 Ом

I₁ = I_вх = 6 А

U_{2 — 3} = I∙R_{2 — 3} — находим напряжение разветвленного участка:

U_{2 — 3} = I∙R_{2 — 3} = 6∙3 = 18 В

U_{2 — 3} = U₂ = U₃ =18 В— т.к. параллельное соединение

А

Дано:

U=240 В

R₁ = 20 Ом

R₂ = 120 Ом

R₃ = 40 Ом

R₄ = 60 Ом

R₅ = 30 Ом

R₆ = 20 Ом

Найти: I_1-6 -?

; R_4-6 = 10 Ом;

;

; R_2-3 = 30 Ом

R_вх=R₁+R_2-3+R_4-6 = 20 + 30 +10 = 60 Ом;

; ;

U_2-3 =I∙R_2-3= 4∙30 = 120 В;

U_{2 — 3} = U₂ = U₃;

;

;

U_4-6=I∙R_4-6=4∙10=40B;

U_4-6=U₄=U₅=U₆;

;

;

;

Дано:

E = 20 В

R_i=2Ом

R₁ = 9Ом

R₂ = 6 Ом

R₃ = 12 Ом

R₄ = 1 Ом

R₅ = 2 Ом

R₆ = 1 Ом

R_4-6 = R₄ + R₅ + R₆;

;

R_3-6 = 3 Ом;

R_вх = R₁ + R_3-6 +R₂ = 9 + 3 + 6 = 18 Ом;

I=;

I=I₁=I₂=1А;

U_3-6=I∙R_3-6=1∙3=3В;

U_3-6=U₃=U_4-6;

I₃=;

I₄=I₅=I₆=;

Cоставим подробное уравнение баланса мощностей для данной схемы. Оно является проверкой правильности решения задачи.

P_u=P_н+Р₀;

EI=I²₁∙ R₁+ I²₂∙ R₂+ I²₃R₃+I₄²R₄+I²₅R₅+I²₆+I²Ri;

20∙1=1²∙9+1²∙6+(0,25)²∙12+(0,75)²∙1+(0,75)²2+(0,75)²1+1²∙2;

20Вт=20Вт- задача решена верно

ДЕЛИТЕЛИ НАПРЯЖЕНИЯ

Делитель напряжения- это четырёхполюсник, у которого коэффициент передачи меньше единицы.

Рассмотрим Г-образный делитель напряжения:

Чтобы рассчитать коэффициент передачи надо:

1) задать произвольное напряжение на входе;

2) любым способом рассчитать напряжение на выходе;

3) взять их отношения:

Для Г-образного делителя напряжения коэффициент передачи равен отношению выходного сопротивления ко входному.

б) Делитель напряжения с плавной регулировкой (потенциометр)

В нижнем положении движка К = 0. В верхнем положении движка К = 1

Так как в нижнем положении движка U_вых снимается с провода, а в верхнем положении

U_вых = U_вх

1) Если нагрузка не подключена делитель работает в режиме холостого хода и зависимость коэффициент передачи от положения движка потенциометра будет линейной.

2) Если подключить нагрузку, то характеристика будет другой: получается параллельное соединение R_н и r и при том же положении движка напряжение участка уменьшается. В крайних точках коэффициент передачи остаётся тем же, поэтому характеристика становиться нелинейной.

Вывод: чтобы при подключении нагрузки характеристика приближалась к линейной нагрузку нужно брать высокоомную.

Тестовые задания:

Задание	Варианты ответов
1.Изменяется ли коэффициент передачи делителя напряжения в пределах 0 ÷ ∞?	Да; Нет.
2.Укажите среди приведенных математических выражений формулы коэффициента передачи по напряжению Г-образного делителя напряжения.	а) ; б); в); г); д).
3.Являются ли характеристики делителя напряжения с плавной регулировкой линейной, если подключить к делителю нагрузки?	Да; Нет.

Соединение резисторов — Основы электроники

Соединение резисторов в различные конфигурации очень часто применяются в электротехнике и электронике.
Здесь мы будем рассматривать только участок цепи, включающий в себя соединение резисторов.
Соединение резисторов может производиться последовательно, параллельно и смешанно (то есть и последовательно и параллельно), что показано на рисунке 1.

Рисунок 1. Соединение резисторов.

Последовательное соединение резисторов

Последовательное соединение резисторов это такое соединение, в котором конец одного резистора соединен с началом второго резистора, конец второго резистора с началом третьего и так далее (рисунок 2).

Рисунок 2. Последовательное соединение резисторов.

То есть при последовательном соединении резисторы подключатся друг за другом. При таком соединении через резисторы будет протекать один общий ток.
Следовательно, для последовательного соединения резисторов будет справедливо сказать, что между точками А и Б есть только один единственный путь протекания тока.
Таким образом, чем больше число последовательно соединенных резисторов, тем большее сопротивление они оказывают протеканию тока, то есть общее сопротивление Rобщ возрастает.
Рассчитывается общее сопротивление последовательно соединенных резисторов по следующей формуле:

Rобщ = R1 + R2 + R3+…+ Rn.

Параллельное соединение резисторов

Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку (Б) (см. рисунок 3).

Рисунок 3. Параллельное соединение резисторов.

При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи (сопротивления между точкой А и Б.)
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением:

1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn

Следует отметить, что здесь действует правило «меньше — меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора.
Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле:

Rобщ= R1*R2/R1+R2

Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них.

Смешанное соединение резисторов

Смешанное соединение резисторов является комбинацией последовательного и параллельного соединения. Иногда подобную комбинацию называют последовательно-параллельным соединением.
На рисунке 4 показан простейший пример смешанного соединения резисторов.

Рисунок 4. Смешанное соединение резисторов.

На этом рисунке видно, что резисторы R2 R3 соединены параллельно, а R1, комбинация R2 R3 и R4 последовательно.
Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов. Далее следуют следующему алгоритму:
1. Определяют эквивалентное сопротивление участков с параллельным соединением резисторов.
2. Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их сопротивление.
3. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.
4. Рассчитывают сопротивления полученной схемы.

Пример расчета участка цепи со смешанным соединением резисторов приведен на рисунке 5.

Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Решение задач на смешанное соединение проводников.

При решении задач на смешанное соединение проводников обычно составляют так называемые эквивалентные схемы, выделяя участки с последовательным и параллельным соединением.

Пример 1.

Сопротивление R_1,2 заменило выделенный участок цепи, в котором два проводника соединены параллельно.

Тогда мы можем найти сопротивление этого участка с параллельным соединением проводников:

А теперь видно, что проводники R_1,2 и R₃ соединены последовательно. Общее сопротивление равно R = R_1,2 + R₃ = 4 + 2 = 6.

Пример 2.

В данном случае нужно развернуть схему, двигаясь от точки к точке. Видно, что в точке Б схема разветвляется, а в точке В ветви соединяются. Таким образом,  эквивалентные схемы будут иметь вид:

R₂, R₃ и R₄ соединены последовательно. Поэтому R_2,3,4 = R₂ + R₃ + R₄ = 1 + 10 + 1 = 12

R_2,3,4 и R₅ соединены параллельно. Поэтому

И в последней схеме проводники соединены последовательно. R = R_2-5 + R₁ + R₆ = 1 + 4,8 + 1 = 6,8.

Пример 3. Найти распределение токов и напряжений в цепи.

Решение.

Так как известны сила тока и сопротивление на первом участке, то можно найти напряжение на нем: U₁ = I₁ R₁ = 1 ∙ 10 = 10 B.

Первый и второй проводники соединены параллельно. Значит, напряжение на них одинаково, т.е. U₁ = U₂ = 10 В. Так как  первый и второй проводники имеют одинаковое сопротивление, то сила тока на них одинакова: I₂ = 1 А. При параллельном соединении I_1,2 = I₁ + I₂ = 2 А.

Участки 1-2, 3-4-5 и 6-7 соединены последовательно между собой, значит I_3,4,5 = I_6,7 = I_1,2 = 2 A.

Найдем общее сопротивление участка 3-4-5:

R_3,4,5 = 3 Ом. Тогда можно найти напряжение на 3-4-5, при параллельном соединении оно одинаково на всех участках. U_3,4,5 = I_3,4,5 ∙R_3,4,5 = 2 ∙ 3 = 6 В.

U₃ = U₄ = U₅ = 6 В. Зная напряжение на каждом из участков и сопротивление, можно найти силу тока на каждом участке.