Поток жидкости и его параметры

Поток жидкости — это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, образующими русло потока. Потоки, имеющие свободную поверхность, называются безнапорными. Потоки, не имеющие свободной поверхности, называются напорными

Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.

Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.

Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Рис. Векторы скорости потока жидкости (а) и живое сечение потока (б)

Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.

Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.

Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.

Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).

Рис. Распределение скоростей движения жидкости в живом сечении трубы при течении: а — турбулентном; б — ламинарном

Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:

Vcр = Sэ/d,
где Sэ — площадь эпюры местных скоростей; d — диаметр трубы

Объемный расход жидкости рассчитывается по формуле:

Q = Sэ*Мср,
где Q — площадь живого сечения потока.

Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.

Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.

Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.

Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.

Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.

Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.

Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.

Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.

Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.

Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.

Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:

Re = vd/V,
где Re — число Рейнольдса; v — средняя скорость потока; d — диаметр трубопровода; V — кинематическая вязкость жидкости.

Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.

Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re < 2320 движение жидкости — ламинарное, а при Re > 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:

vкр = 2320v/d

Расчет диаметра трубопровода, скорости потока рабочей жидкости

Расчет диаметра трубопровода, скорости потока рабочей жидкости

При проведении расчетов по определению диаметра трубопровода (магистрали) и скорости прохождения по нему рабочей жидкости необходимо учитывать его принципиальное назначение. Магистрали гидравлической системы делятся на всасывающие, напорные и сливные.

Ниже приведена справочная информация, по рекомендуемой скорости прохождения потока жидкости в трубопроводах и магистралях гидропривода.

При проектировании (объемного гидропривода) расчетная скорость жидкости (ед. измерения, м/с) должна быть в пределах указанных значений справочной таблицы.

 Для вычисления скоростного показателя V рабочей жидкости (единица измерения м/сек), используются параметры:

1) Внутренний диаметр применяемой трубы диаметр d (мм)
2) Подача от гидравлического насоса Q (л/мин)

Для правильного подбора соответствующего диаметра магистрали (напорной, всасывающей и сливной)

1) Подберите в предложенном справочном блоке, оптимальный скоростной показатель для рассчитываемого трубопровода V, (м/сек)
2) Заполните форму подача насоса

Q (л/мин)

Далее нажимаем «Вычислить d», для получения рассчитываемого параметра.

 

Заполните формы 

Справочный блок рекомендуемой скорости прохождения потока в трубопроводе:

назначение	скорость	допустимая скорость потока жидкости
1. Всасывающий трубопровод	v	от 0.50 до 1 м/сек.
2. Сливной трубопровод	v	от 1.250 до 3 м/сек.
3. Напорный трубопровод	v	3.20 м/сек. при давлении свыше 100 бар,(10МПа)
4. Напорный трубопровод	v	от 3.50 до 5 м/сек. при давлении свыше 150 бар,(15МПа)
5. Напорный трубопровод	v	от 5.250 до 7 м/сек. при давлении свыше 200 бар,(20МПа)
6. Напорный трубопровод	v	от 7.250 до 9 м/сек. при давлении свыше 350 бар,(35МПа)

Если давление в МПа необходимо произвести пересчет их в бары, прим.(1МПа = 10 бар)

Примечание, для разделения разрядов используйте «.»(точка)

 

Типичные скорости (практические скорости) потока жидкости (воды) в трубопроводах (трубах) в различных технологичеcких и коммунальных сетях.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Инженерное ремесло / / Падение давления, потери давления на трение.  / / Типичные скорости (практические скорости) потока жидкости (воды) в трубопроводах (трубах) в различных технологичеcких и коммунальных сетях. Поделиться:    Типичные скорости (практические скорости) потока жидкости в трубопроводах (трубах) в различных технологических и коммунальных сетях. Водопровод. Канализация. Теплоснабжение (отопление). Комфортной (не вызывающей излишней коррозии / эрозии или шума в трубопроводах) считается скорость до 1,5 м/с. Приемлемой — до 2,5 м/с. А практически встречающиеся скорости см. в таблице ниже: Система Диапазон практических скоростей (м/с) Самоциркулирующее теплоснабжение — скорость потока 0,2-0,5 Теплоснабжение с принудительной циркуляцией основная «прямая труба» — скорость потока 0,5-3 (выше — не стоит подключать новые нагрузки) Теплоснабжение с принудительной циркуляцией — отводы на батареи = радиаторы — скорость потока 0,2-0,5 Водоснабжение магистральное — скорость потока 0,5-4 (выше — не стоит подключать новые нагрузки) Водоснабжение ХВС и ГВС (разбор воды) — скорость потока 0,5-1 (выше — потребители не оценят фонтан…) Циркуляция в системе ГВС — скорость потока 0,2-0,5 ( выше никому не нужно) Промышленное холодоснабжение основная «прямая труба» — скорость потока 0,5-3 (до 5 м/с) Промышленное холодоснабжение отводы на холодильные радиаторы камер — скорость потока 0,2-0,5 Канализация, безнапорная, в том числе ливневая — скорость потока 0,5-1 (до 3 м/с) Дополнительная информация: «… Скорость потока учитывается только для определения диаметра трубопровода. При неправильном выборе диаметра (скорость потока для: жидкой среды от 3 до 10 м/с; газообразной — свыше 20 м/с) будет наблюдаться повышенная вибрация трубопровода и образование статического электричества. Кавитация от скорости не зависит, а только от перепада давления и давления насыщенных паров перекачиваемой жидкости.» ТПА номер 5(86) 2016 г — Якименко В.К. ЗАО «ТюменьВНИПИнефть» Поиск в инженерном справочнике DPVA. Введите свой запрос:

Как посчитать скорость потока жидкости в трубе?

Объёмный расход V (60м&#179/час или 60/3600м&#179/сек) рассчитывается как произведение скорости потока w на поперечное сечение трубы S (а поперечное сечение в свою очередь считается как S=3.14 d&#178/4): V = 3.14 w d&#178/4. Отсюда получаем w = 4V/(3.14 d&#178). Не забудьте перевести диаметр из миллиметров в метры, то есть диаметр будет 0.159 м.

поставить спидометр на трубу

<img src=»//content.foto.my.mail.ru/mail/nice.zlatan/_answers/i-4.jpg» > где &#961; — плотность жидкости, кг/м&#179;; p1 &#8722; p2 = &#916;p — перепад давления на концах капилляра, Па; Q — поток жидкости, м&#179;/с; R — радиус капилляра, м; d — диаметр капилляра, м; &#956; — вязкость жидкости, Па·с; l — длина трубы, м.

159 делить на 60 в кубе и подставляем в уравнение Максвелава

У тебя, собстенно все есть v *S = W, w — расход, v-что ищешь, S площадь сечения трубы v = W/S v=60 / (3600*Pi *(0.159)^2/4)= 0.84 м/сек

Площадь сечения трубы раздели на давление воды получишь скорость потока.

НУ поставь спидометр

0.84 м/сек считал на калькуляторе скорости воды в трубопроводе <a rel=»nofollow» href=»http://allcalc.ru/node/826″ target=»_blank»>http://allcalc.ru/node/826</a>

Онлайн калькулятор расчета скорости воды и газа в трубе

Автоматизированный расчет скорости движения потока в трубопроводе нашим калькулятором будет необходим в том случае, если Вы решили провести канализацию, отопительную или водопроводную систему своими руками в частном доме. Расчет поможет определиться в выборе диаметра трубы, его протяженности или количестве поворотов трубопровода.

Онлайн калькулятор для подсчета скорости воды и газа в трубопроводе

Рассчитать все параметры перемещения жидкости в водопроводной системе, вопреки кажущейся простоте, представляет собой сложную задачу, поскольку на поток воды действует одновременно множество разноречивых факторов.

Зачем нужен расчет

Каковы основные направления использования воды в здании? Их несколько:

1. Потребление для санитарных, а также бытовых нужд.
2. Устройство отопления с водяным теплоносителем.
3. Водопровод системы пожаротушения.
4. Система канализации стоков.

Каждое направление имеет свои особенности и характеристики по условиям эксплуатации. При недостаточной мощности трубопроводной системы возможно критично резкое снижение давления, а вероятность получения слабой струйки из пожарного шланга испортит настроение любому.

Скорость течения стоков по системе канализации также имеет особое значение, поскольку малейший просчет в угле наклона отрицательно сказывается  на работе такого водопровода и его долговечности. Недостаточный угол предполагает возможность остановки действия, а излишний приводит к ускоренному засорению канала.

Влияние различных факторов на работу водопроводной сети

На первый взгляд механизм простой – есть магистраль с определенным диаметром и чем большего оно размера, тем больше пройдет по ней жидкости при определенном давлении.

Безусловно, это действенные факторы, влияющие на расход воды и интенсивность ее перемещения по водопроводной сети. Но это только начало длинного перечня, поскольку кроме них существуют и другие воздействия:

1. Длина трубы. По мере перемещения жидкость испытывает обратное направлению потока воздействие от трения о стенки трубы. Величина сопротивления такова, что пренебречь ею невозможно. Разумеется, на консоли через сливное отверстие скорость истечения зависит только от давления. Но вытекшую жидкость нужно заместить, а быстрота ввиду сопротивления недостаточна.
2. Прямое воздействие на скорость течения жидкости оказывает диаметр внутреннего сечения трубопровода. Чем он меньше, тем более сильное сопротивление потоку оказывается, поскольку площадь контакта по отношению к объему протекающей воды увеличивается. То есть, между этими параметрами существует обратно пропорциональная зависимость.
3. Материал, из которого изготовлена круглая труба, также оказывает существенное влияние. Внутренняя поверхность пластиковых изделий, изготовленных из сшитого полиэтилена, более гладкая, чем у аналогичных из металла. Она оказывает гораздо меньшее сопротивление потоку. Более того, при расчете скорости жидкости в трубопроводе, изготовленном из металла, следует понимать, что он справедлив только для новой системы. Такие системы очень быстро засоряются известковыми отложениями на внутренних стенках и продуктами окисления металла. Учесть такие воздействия невозможно, поскольку интенсивность их накопления во многом зависит от качества воды. Величина сопротивления в новой трубе и засоренной может возрастать до 200 раз.
4. Скорость движения жидкости в трубопроводной системе во многом зависит от ее сложность. Каждый поворот, каждый фитинг – это потеря скорости, причем степень влияния не ограничивается статистической погрешностью, а снижает проходимость многократно.

Учитывая сказанное, очевидно, что достоверно определить основные параметры действия водопровода гидравлическим расчетом практически невозможно. Тем не менее, расчет скорости воды в трубопроводе необходим для определения первичных данных по его основным характеристикам и делать его нужно с использованием калькулятора, используя  режим online.

1.4 Режимы течения жидкости в трубах

Возможны два режима течения жидкостей в трубах: ламинарный и турбулентный.

Ламинарным называют слоистое течение жидкости без перемешивания её частиц и без пульсаций скоростей и давлений. Частицы жидкости при таком режиме движутся параллельно стенкам трубопровода.

Турбулентным называют течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение частиц жидкости при таком режиме приобретает беспорядочный характер.

Режим течения данной жидкости в данной трубе изменяется при определенной скорости течения v_кр, которую называют критической:

, м/с,

где d – внутренний диаметр трубы, мм;

Re_кр – критическое число Рейнольдса;

–коэффициент кинематической вязкости, сСт.

Для гладких металлических труб круглого сечения Rе_кр=2200-2300; для резиновых рукавов Re_кр=1600.

Чтобы определить режим течения жидкости в трубе, рассчитывают среднюю скорость движения жидкости v и число Рейнольдса Re. Так, для трубы круглого сечения:

где Q – расход жидкости, л/мин; d, мм; , сСт.

При Re<Re_кр течение является ламинарным, при Re>Re_кр — турбулентным. (При Re=Re_кр, например для труб, в интервале 2200-2300 возможны неустойчивость режима течения и возникновение колебательного процесса).

В гидросистемах станков, предназначенных для обеспечения малых скоростей движения рабочих органов, режим течения жидкостей в трубах преимущественно ламинарный. При больших скоростях движения масла (6-7 м/с) в трубопроводах возможен турбулентный режим.

Распределение скоростей в поперечном сечении турбулентного и ламинарного потоков существенно различается. Распределение скоростей при турбулентном течении более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении, для которого характерен параболический закон распределения скоростей (рис. А3).

Рис. А3

Рекомендуется обеспечивать следующие скорости движения масла в трубопроводах гидросистем станков:

— всасывающих – до 1,6 м/с,

— напорных – до 2-5 м/с (при больших давлениях – до 10 м/с),

— сливных – 2 м/с.

1.5 Гидравлические потери

Разность давлений масла в двух сечениях одного и того же трубопровода при условии, что первое расположено выше по течению, а второе – ниже, определяется уравнением Бернулли:

,

где h₂ – h₁ – разность высот центров тяжести сечений от произвольно выбранного горизонтального уровня;

v₁, v₂ – cредние скорости масла в сечениях;

g – ускорение силы тяжести;

–сумма гидравлических потерь при движении масла из первого сечения во второе.

Уравнение Бернулли в полном виде используется для расчета всасывающих линий насосов; в остальных случаях первым слагаемым, как правило, пренебрегают и считают:

Гидравлические потери обычно разделяют на местные потери и потери на трение по длине трубопровода (линейные).

1.5.1 Местные потери энергии обусловлены местными гидравлическими сопротивлениями, вызывающими деформацию потока. Местными сопротивлениями являются: сужения, расширения, закругления трубопроводов, фильтры, аппаратура управления и регулирования и пр. При протекании жидкости через местные сопротивления изменяется её скорость и обычно возникают крупные вихри.

Потери давления от местных сопротивлений определяют по формуле Вейсбаха:

МПа (или Па),

где  (кси) – коэффициент сопротивления или потерь,

v – средняя по сечению скорость потока в трубе за местным сопротивлением, м/с; , Н/м³; g=9,81 м/с².

Каждое местное сопротивление характеризуется своим значением коэффициента . При турбулентном течении значенияопределяются, в основном, формой местных сопротивлений и очень мало изменяются с изменением размеров сечения, скорости потока и вязкости жидкости. Поэтому принимают, что они не зависят от числа Рейнольдса Re.

Значения , например, для тройников с одинаковыми диаметрами каналов, принимают равными, если:

потоки складываются, расходятся; поток проходящий;

=0,5-0,6 =1,5-2=0,3=1-1,5=0,1=0,05

=0,7 =0,9-1,2=2

при повороте трубопровода = 1,5-2 и т.д. [с. 390-391]

Значения для конкретных сопротивлений, встречающихся в гидросистемах оборудования, берут из справочной литературы.

При ламинарном режиме (Re<2200) потери давления зависят, в основном, от гидравлического трения в местных сопротивлениях, а значит, при их определении надо учитывать величину Re.

Потери давления от местных сопротивлений при ламинарном режиме определяются по формуле:

МПа,

где _л = аи поправочный коэффициент ламинарности

Величины потерь давления в стандартных гидравлических устройствах для номинального расхода жидкости обычно приводятся в их технических характеристиках.

1.5.2 Потери на трение по длине — это потери энергии, которые возникают в прямых трубах постоянного сечения, т.е. при равномерном течении жидкости, и возрастают пропорционально длине трубы. Эти потери обусловлены внутренним трением в жидкости, а поэтому имеют место и в шероховатых, и в гладких трубах.

Потери давления на трение в трубопроводе определяется по формуле Дарси:

МПа,

где – коэффициент трения в трубопроводе;

l и d – длина и внутренний диаметр трубопровода, мм.

Эта формула применима как при ламинарном, так и при турбулентном течении; различие заключается лишь в значениях коэффициента .

При ламинарном режиме (Re<2200) коэффициент трения является функцией основного критерия напорных потоков — числа Рейнольдса и рассчитывается по формуле:

При турбулентном течении коэффициент трения является не только функцией числа Re, но зависит и от шероховатости внутренней поверхности трубы. Для гидравлически гладкой трубы, т.е. с такой шероховатостью, которая практически не влияет на ее сопротивление, коэффициент трения при турбулентном режиме можно определить по формуле П.К. Конакова:

Трубу считают гидравлически гладкой, если (d/k)>(Re/20), где k – эквивалентная шероховатость, мм. Например, для новых бесшовных стальных труб k≈0,03 мм, а после нескольких лет эксплуатации k≈0,2 мм, для новых цельнотянутых труб из цветных металлов k≈0,005 мм. Такие трубы часто используются в гидросистемах металлорежущих станков.

Коэффициент трения при турбулентном режиме можно определить по формуле Альтшуля, являющейся универсальной (т.е. применимой в любых случаях):

Примеры гидравлических расчетов

Пример 4.1. Определить пределы изменения гидравлического радиуса R для канализационных самотечных трубопроводов, если их диаметр d изменяется от 150 до 3500 мм. Расчетное наполнение принять: a = h/d = 0,6 для труб диаметром d = 150 мм; a = h/d = 0,8 для труб диаметром d = 3500 мм.

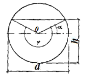
Решение:

Гидравлический радиус определяем по формуле

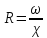
где площадь живого сечения

,

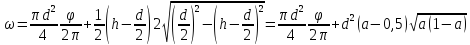смоченный периметр .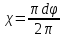

Угол α находим из соотношения

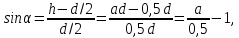
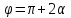
Проведем расчеты:

— для трубы диаметром d = 150 мм

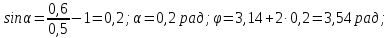
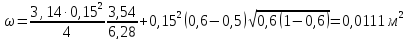
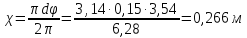
Тогда гидравлический радиус равен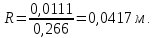

— для трубы диаметром d = 3500 мм

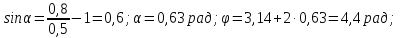
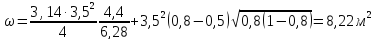
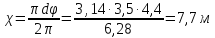
Тогда гидравлический радиус равен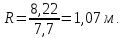

Таким образом, гидравлический радиус изменяется от 0,04 до 1,07 м.

Пример 4.2. Определить режим движения воды в водопроводной трубе диаметром d = 300 мм, если протекающий по ней расход Q = 0,136 м³/с. Температура воды 10°С.

Решение:

Число Рейнольдса находим по формуле:

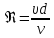
Средняя скорость движения воды в трубе

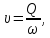
где живое сечение потока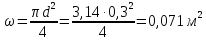

Тогда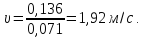

Кинематический коэффициент вязкости воды при температуре 10°С находим по таблице 4.5 (Приложение 4): ν = 0,0131·10^-4м²/с.

Следовательно,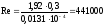

Так как 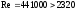значит режим движения турбулентный.

Методические рекомендации к проведению расчетов

Для того чтобы определить режим движения жидкости, необходимо рассчитать число Рейнольдса Re по формуле (4.3) для труб круглого сечения и по формуле (4.4) для трубы произвольного сечения. В последнем случае гидравлический радиус рассчитывается по формуле (4.1) (пример 4.1). Затем сравнить полученное значение Re c критическим Re_кр=2320 (пример 4.2).

Значение критической скорости определяется по формуле (4.5), а соответствующий ей расход по формуле (4.2).

Задачи

Задача 4.1. Жидкость движется в лотке со скоростью V = 0,1 м/с. Глубина наполнения лотка h = 30 см, ширина по верху В = 50 см, ширина по низу b = 20 см. Определить смоченный периметр, площадь живого сечения, гидравлический радиус, расход, режим движения жидкости, если динамический коэффициент вязкости жидкости μ = 0,0015 Па·с, а ее плотность ρ = 1200 кг/м³.

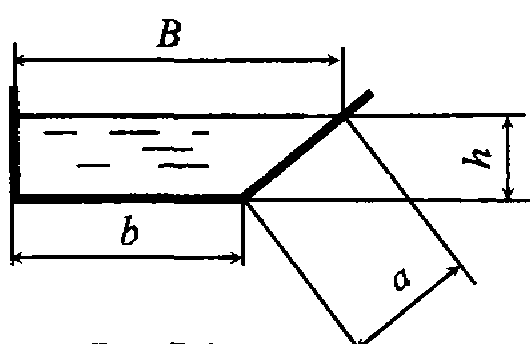
Задача 4.2. Найти минимальный диаметр d напорного трубопровода, при котором нефть будет двигаться при турбулентном режиме, если кинематический коэффициент вязкости нефти ν = 0,3 см²/с, а расход в трубопроводе Q = 8 л/с.

Задача 4.3. По трубе диаметром d = 0,1 м под напором движется вода. Определить расход, при котором турбулентный режим сменится ламинарным, если температура воды t = 25°C.

Задача 4.4. Определить критическую скорость, при которой происходит переход от ламинарного режима к турбулентному, в трубопроводе диаметром d = 30 мм при движении воды (ν = 0,009 Ст), воздуха (ν = 0,162 Ст) и глицерина (ν = 4,1 Ст).

Задача 4.5. Определить, изменится ли режим движения воды в напорном трубопроводе d = 0,5 м при возрастании температуры от 15 до 65°С, если расход в трубопроводе Q = 15 л/с.

Задача 4.6. Вода движется под напором в трубопроводе прямоугольного сечения. Определить при каком максимальном расходе сохранится ламинарный режим. Температура воды t = 30°C, а = 0,2 м, b = 0,3 м.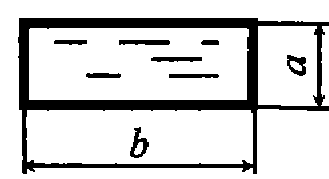

Задача 4.7. По трубе диаметром d = 0,1 м под напором движется вода. Определить расход, при котором турбулентный режим сменится ламинарным, если температура воды t = 25°C.

Задача 4.8. Жидкость движется в безнапорном трубопроводе с расходом Q = 22 м³/ч. Трубопровод заполнен наполовину сечения. Диаметр трубопровода d = 80 мм. Определить, при какой температуре будет происходить смена режимов движения жидкости. График зависимости кинематического коэффициента вязкости представлен на рисунке.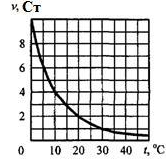

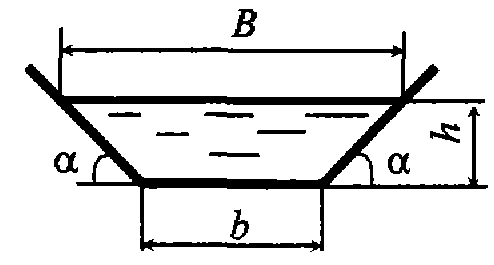
Задача 4.9. Жидкость, имеющая динамический коэффициент вязкости μ = 1,005 Па·с и плотность ρ = 900 кг/м³, движется в трапецеидальном лотке. Определить критическую скорость, при которой будет происходить смена режимов движения жидкости. Глубина наполнения h = 0,2 м, ширина лотка по дну b = 25 см, угол наклона боковых стенок лотка к горизонту α = 30°.

Задача 4.10. Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр d = 12 мм и максимальный диаметр d = 3500 мм. Расчетные скорости движения воды в них V = 0,5÷4 м/с. Определить минимальное и максимальное значение чисел Рейнольдса и режим течения в этих трубопроводах.

Задача 4.11. Для осветления сточных вод используют горизонтальный отстойник, представляющий собой удлиненный прямоугольный резервуар. Его глубина h = 2,6 м, ширина b = 5,9 м. Температура воды t = 20°С. Определить среднюю скорость и режим движения сточной жидкости, если ее расход Q = 0,08 м³/с, а коэффициент кинематической вязкости ν = 1,2·10^-6 м²/с. При какой скорости в отстойнике будет наблюдаться ламинарный режим движения жидкости?

Задача 4.12. Конденсатор паровой турбины оборудован 8186 трубками диаметром d = 2,5 см. Через трубки пропускается охлаждающая вода при t = 10°С. Будет ли при расходе воды Q = 13600 м³/с обеспечен турбулентный режим движения в трубках?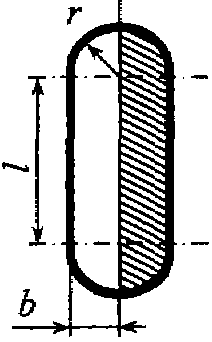

Задача 4.13. Определить режим движения горячей воды (t = 80°С) в пробковом кране, проходное сечение которого при частичном открытии изображено на рисунке, если l = 20 мм, b = r = 3 мм, расход воды Q = 0,1 л/с.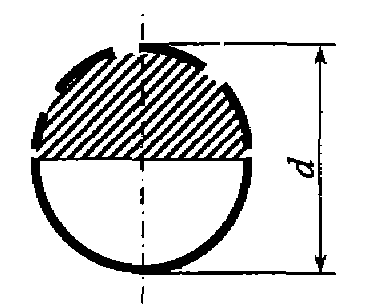

Задача 4.14. Определить режим движения воды при t = 20°С в смесителе, проходное сечение которого открыто наполовину, если d = 10 мм, расход воды Q = 0,1 л/с.

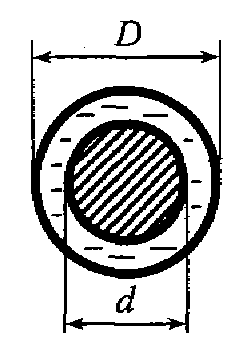
Задача 4.15. Смазка протекает через кольцевую щель. Определить гидравлический радиус при условии, что D = 50 мм, d = 48 мм.

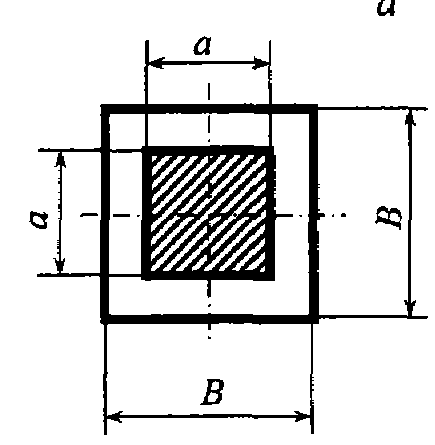
Задача 4.16. Определить гидравлический радиус для формы потока, изображенной на рисунке.

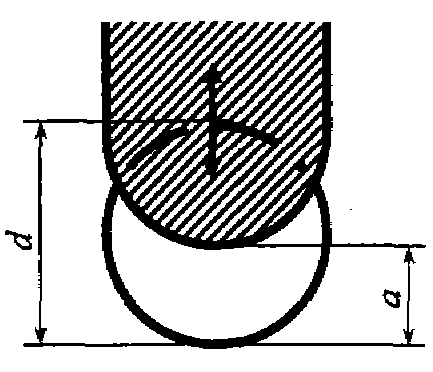
Задача 4.17. Определить гидравлический радиус, если простая задвижка на трубе круглого сечения d частично закрыта,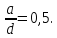

Задача 4.18. Построить эпюру скоростей и касательных напряжений в сечении трубы диаметром d = 50 мм, если расход потока Q = 100 см³/с, а температура воды t = 8°С.

Задача 4.19. Определить максимальную и среднюю в сечении скорости, построить эпюру скоростей потока нефти в трубе диаметром d = 400 мм, если расход потока Q = 15 л/с, коэффициент кинематической вязкости ν = 0,29 см²/с.

Задача 4.20. Построить эпюру осредненных скоростей в сечении трубы, по которой протекает поток бензина с расходом Q = 60 л/с, если диаметр трубы d = 350 мм, кинематический коэффициент вязкости ν = 0,0093 Ст. Гидравлический коэффициент трения λ = 0,03.