Лабораторная работа № 3. Исследование разветвленной линейной электрической цепи постоянного тока. Закон кирхгофа
ЦЕЛЬ РАБОТЫ
Экспериментальное исследование характеристик цепи, построение потенциальной диаграммы, освоение основных расчетных приемов по определению токов и напряжений на участках цепи.
ОСНОВЫ ТЕОРИИ
Величина тока в неразветвленной электрической цепи с несколькими источниками определяется отношением алгебраической суммы ЭДС всех источников к полному сопротивлению цепи .
Напряжение на зажимах источника, работающего в режиме потребителя, больше,чем ЭДС самого источника на величину падения напряжения на внутреннем сопротивлении этого источника.
Напряжение на клеммах источника, работающего в режиме генератора, меньше, чем ЭДС источника на величину падения напряжения на внутреннем сопротивлении этого источника:.
Напряжение на любом участке .
Потенциальная диаграмма представляет собой график изменения потенциалов точек цепи от величины сопротивлений участков между этими точками.
Первый закон Кирхгофа: алгебраическая сумма токов в ветвях, соединенных в один узел, равна нулю. Токи, входящие в узел, принято считать положительными, а выходящие – отрицательными.
Второй закон Кирхгофа: алгебраическая сумма ЭДС в замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на всех участках этой цепи, т.е. . ЭДС источника, совпадающая с выбранным направлением обхода контура, считается положительной, а не совпадающая – отрицательной.
Метод свертывания
Схема упрощается по возможности до такой, в которой применим закон Ома.
Метод наложения
В каждой ветви рассматриваемой цепи направление тока выбирается произвольно.
Количество расчетных схем цепи равно количеству источников в исходной схеме.
Вкаждой расчетной схеме действует только один источник, а остальные источники заменяются их внутренними сопротивлениями.
В каждой расчетной схеме методом свертывания определяют частичные токи каждой ветви.
Искомые токи каждой ветви рассматриваемой схемы определяются как алгебраическая сумма частичных токов в этой ветви.
Метод контурных токов
Является одним из основных методов расчета сложных цепей. Он заключается в том, что вместо токов в ветвях определяются на основании 2-го закона Кирхгофа так называемые контурные токи. При этом исключаются уравнения 1-го закона Кирхгофа. Уравнения могут быть записаны, если приписать каждой ячейке некоторый контурный ток, совпадающий с током внешних ветвей.
Метод узловых потенциалов
Этот метод позволяет уменьшить число уравнений Кирхгофа за счет исключения уравнений 2-го закона. На схеме принимаем потенциал точки О равным нулю.
Метод расчета тока в выделенной ветви, основанный на замене активного двухполюсника эквивалентным генератором, принято называть методом эквивалентного генератора, а также методом холостого хода и короткого замыкания.
Рекомендуется такая последовательность расчета тока этим методом:
Найти напряжение на зажимах разомкнутой ветви 12;
Определить входное сопротивлениевсей схемы по отношению к зажимам 12 при закороченных источниках ЭДС и разомкнутых ветвях с источниками тока;
Подсчитать ток по формуле , если сопротивление ветви 12 равно нулю(), то для нее имеет место режим короткого замыкания, а протекающий в ней ток есть ток короткого замыкания
Потенциальной диаграммой называют график, на котором по оси абсцисс откладывают сопротивления резисторов, а по оси ординат – потенциалы соответствующих точек электрической схемы. Сопротивления резисторов откладывают поочередно друг за другом в том порядке, в котором они следуют при обходе исследуемого участка цепи.
Баланс мощностей
При протекании токов по сопротивлениям в последних выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях схемы, должно равняться энергии, доставляемой за то же время источником питания. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид .
Когда схема питается не только от источников ЭДС, но и от источников тока, т.е. к отдельным узлам схемы подтекают и от них утекают токи источников тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Допустим, что к 1-му узлу схемы подтекает ток , а от 2-го узла он утекает. Доставляемая источником тока мощность равна. Тогда общий вид уравнения энергетического баланса имеет вид.
ПРЕДВАРИТЕЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ
Для схемы составить для всех узлов и ветвей уравнения Законов Кирхгофа.
Определить токи в ветвях используя законы Кирхгофа или метод контурных токов.
Построить потенциальную диаграмму.
Составить баланс мощностей.
ПОДГОТОВКА К РАБОТЕ И ПРОГРАММА ЕЕ ПРОВЕДЕНИЯ
Изучить схему постоянного тока, записать величины сопротивлений входящих в нее резисторов и определить основные характеристики приборов (пределы измерения и класс точности).
.Начертить схему проведения эксперимента.
Рис. 1. Схема цепи постоянного тока
Собрать схему проведения эксперимента и произвести замеры.
Сравнить результаты расчета и эксперимента.
На миллиметровой бумаге построить потенциальную диаграмму.
Подготовить бланк отчета.
Исходные данные для проведения лабораторной работы
Гр. | E | R1 | R2 | R3 | R4 | R5 | I1 | I2 |
1 | 6 | 2 | 5 | 4 | 3 | 1 | 1 | 5 |
2 | 8 | 4 | 3 | 4 | 1 | 3 | 2 | 3 |
3 | 10 | 6 | 2 | 1 | 3 | 5 | 2 | 6 |
4 | 12 | 1 | 7 | 4 | 5 | 1 | 4 | 5 |
5 | 5 | 3 | 4 | 6 | 2 | 1 | 3 | 1 |
6 | 7 | 5 | 2 | 2 | 1 | 6 | 4 | |
7 | 9 | 2 | 1 | 4 | 1 | 4 | 2 | 7 |
8 | 11 | 6 | 3 | 4 | 2 | 2 | 3 | 5 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
Что называется узлом и контуром электрической цепи?
Могут ли токи в ветвях и потенциалы точек иметь отрицательное значение?
Как построить потенциальную диаграмму?
Как используются законы Кирхгофа для расчета сложных электрических цепей?
Дайте определение первого и второго законов Кирхгофа.
В чем заключается метод контурных токов?
Лабораторная работа № 4 ИССЛЕДОВАНИЕ МНОГОКОНТУРНОЙ СИСТЕМЫ ПОСТОЯННОГО ТОКА
ЦЕЛЬ РАБОТЫ
Экспериментальное исследование сложных многоконтурных систем постоянного тока и преобретениенавыков расчета таких цепей.
ПРЕДВАРИТЕЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ
Для схемы составить для всех узлов и ветвей уравнения Законов Кирхгофа.
Определить токи в ветвях, используя любой из методов
Составить баланс мощностей.
ПОДГОТОВКА К РАБОТЕ И ПРОГРАММА ЕЕ ПРОВЕДЕНИЯ
Начертить схему проведения эксперимента, предварительно подключив необходимые приборы.
Изучить схему постоянного тока, записать величины сопротивлений входящих в нее резисторов и определить основные характеристики приборов (пределы измерения и класс точности).
Проведение работы.
Сравнить результаты расчета и эксперимента, сделать вывод.
Рис. 1. Схема многоконтурной цепи постоянного тока
Исходные данные для проведения лабораторной работы
Гр. | R1 | R2 | R4 | R5 | R6 | E1 | E2 | E3 | E4 |
1 | 10 | 10 | 7 | 5 | 15 | 100 | 30 | 10 | 6 |
2 | 5 | 15 | 6 | 4 | 12 | 60 | 10 | 24 | 12 |
3 | 15 | 5 | 4 | 8 | 20 | 120 | 24 | 6 | 3 |
4 | 3 | 10 | 2 | 5 | 15 | 50 | 8 | 16 | 9 |
5 | 10 | 4 | 3 | 6 | 12 | 80 | 20 | 6 | 3 |
6 | 12 | 12 | 8 | 7 | 18 | 120 | 60 | 12 | 10 |
7 | 16 | 10 | 4 | 15 | 5 | 100 | 12 | 60 | 24 |
8 | 8 | 5 | 2 | 6 | 6 | 110 | 12 | 24 | 12 |
КОНТРОЛЬНЫЕ ВОПРОСЫ.
Что называется узлом и контуром электрической цепи?
Могут ли токи в ветвях и потенциалы точек иметь отрицательное значение?
Как построить потенциальную диаграмму?
Как по потенциальной диаграмме определить напряжение между двумя точками?
Как используются законы Кирхгофа для расчета сложных электрических цепей?
Дайте определение первого и второго законов Кирхгофа.
В чем заключается метод контурных токов?
studfile.net
Лабораторная работа 3 разветвленная линейная электрическая цепь постоянного тока
Цель работы: получение навыков сборки электрических цепей, измерений токов и напряжений на отдельных участках электрической цепи; убедиться в соблюдении законов Кирхгофа в разветвленной линейной электрической цепи; научиться применять законы Кирхгофа в графическом виде.
Оборудование: лабораторный стенд, соединительные провода, резистор 2 Вт 68 Ом, резистор 2 Вт 150 Ом, резистор 2 Вт 330 Ом, потенциометр ППБ-3А-150 Ом.
Порядок выполнения работы
Ознакомиться с лабораторной установкой (источник питания, функциональный генератор, измеритель мощности, мультиметр, цифровые амперметры РА1…РА4, наборное поле и минимодули резисторов).
Собрать линейную цепь со смешанным соединением резисторов (рис. 1). В качестве амперметров использовать цифровые приборы в режиме измерения постоянного тока. В качестве вольтметра использовать стрелочный вольтметр PV1. представить схему для проверки преподавателю.
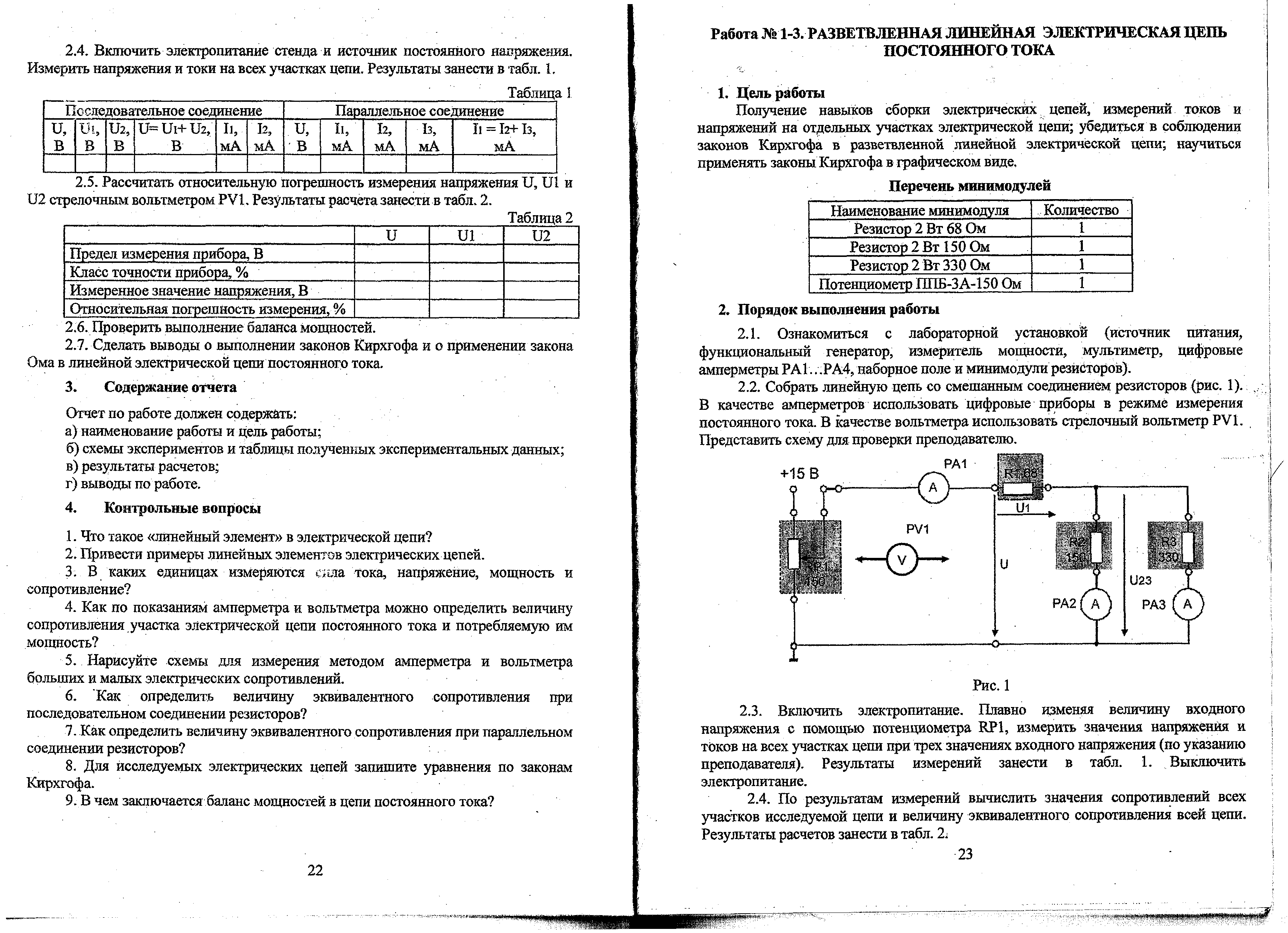
Рис. 1
Включить электропитание. Плавно изменяя величину входного напряжения с помощью потенциометра RP1, измерить значения напряжения и токов на всех участках цепи при трех значениях входного напряжения (по указанию преподавателя). Результаты измерений занести в табл. 1. Выключить электропитание.
Таблица 1
№ опыта | U, В | U1, В | U23, В | U = U1 + U23, В | I1, мА | I2, мА | I3, мА | I1 = I2 + I3, мА |
1 | ||||||||
2 | ||||||||
3 |
По результатам измерений вычислить значения сопротивлений всех участков исследуемой цепи и величину эквивалентного сопротивления всей цепи. Результаты расчетов занести в табл. 2.
Таблица 2
Резистор | Вычислено |
R1, Ом | |
R2, Ом | |
R3, Ом | |
Rэкв, Ом |
По результатам измерений построить в одной координатной системе вольтамперные характеристики резисторов R1, R2, R3. Пользуясь ими, построить вольтамперную характеристику всей цепи Uвх = f (I1) и по ней определить эквивалентное сопротивление цепи Rэкв. Здесь же построить экспериментальную вольтамперную характеристику цепи Uвх = f (I1), сравнить ее с расчетной вольтамперной характеристикой всей цепи и сделать вывод о возможности графического применения законов Кирхгофа.
Сделать вывод о возможности применения законов Кирхгофа в графическом виде в электрической цепи постоянного тока.
Содержание отчета:
Наименование работы и цель работы.
Схемы экспериментов и таблицы полученных экспериментальных данных.
Результаты расчетов.
Выводы по работе.
Контрольные вопросы:
Как по показаниям амперметра и вольтметра можно определить величину сопротивления участка электрической цепи постоянного тока и потребляемую им мощность?
Нарисуйте схемы для измерения методом амперметра и вольтметра больших и малых электрических сопротивлений.
Как определить величину эквивалентного сопротивления для исследуемой цепи?
Для исследуемых электрических цепей запишите уравнения по законам Кирхгофа.
Как по вольтамперной характеристике определить величину сопротивления цепи?
studfile.net
Расчет линейных электрических цепей постоянного тока
Расчет неразветвленных цепей
Основой расчета одноконтурных (неразветвленных) электрических цепей, содержащих источники обоих видов и потребители, служат рассмотренные ранее законы Ома и Кирхгофа.
Если в цепи нет источников тока, а параметры потребителей (R) и источников напряжения (Е) заданы, то задача обычно состоит в определении тока контура. Положительное направление искомого тока выбирается произвольно и составляется уравнение:
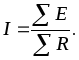 (2.1)
(2.1)
При этом необходимо помнить, что со знаком «+» берутся ЭДС источников, которые действуют в направлении выбранного тока. Истинное направление совпадает с выбранным, если в результате расчета ток оказывается положительной величиной, и противоположно выбранному, если ток оказывается отрицательным.
Если в цепи, кроме
потребителе (R)
и источников ЭДС (E),
имеется источник тока (J),
то задача обычно сводится к определению
напряжения на источнике тока UJ,
т.к. ток контура I совпадает
с заданным током источника J. Положительная полярность UJ выбирается
произвольно, но предпочтительно у острия
стрелки ставить знак «+» (такой полярности
соответствует формула: 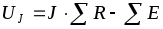 ).
Истинная полярностьUJ совпадает
с выбранной, если при расчете UJ выражается
положительным числом, и противоположна
выбранной, если UJ<
0. Искомое
падение напряжения на источнике тока UJ при отсутствии источников ЭДС определяется
по формуле
).
Истинная полярностьUJ совпадает
с выбранной, если при расчете UJ выражается
положительным числом, и противоположна
выбранной, если UJ<
0. Искомое
падение напряжения на источнике тока UJ при отсутствии источников ЭДС определяется
по формуле 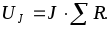 .
.
Расчет разветвленных цепей с одним источником
Разветвленную цепь с одним источником обычно упрощают, преобразуя в неразветвленную (рис. 2.1.), и решают методами, изложенными выше. Основная проблема состоит в нахождении токов и напряжений ветвей исходной схемы, поскольку в результате преобразования такие ветви не сохраняются.
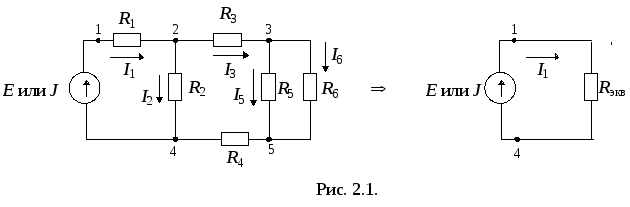
Для определения токов и напряжений в схеме рис. 2.1. сначала определяется Rэкв смешанного соединения потребителей относительно зажимов источника (точки 1 и 4 на рис. 2.1.). Затем, если цепь питается источником напряжения, то определяется ток по формуле:
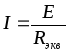
Если цепь питается источником тока, то определяется напряжение
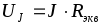
Порядок дальнейшего расчета одинаков для обоих случаев, т.к. известны E или UJ и I или J неразветвленной части схемы. Рассмотрим порядок расчета для представленной на рис. 2.1 цепи.
Ток в потребителе R1 совпадает с найденным током неразветвленной
части I, а напряжение 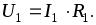
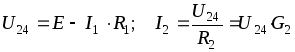 .
.
Ток I3 определяется
по закону Кирхгофа: 
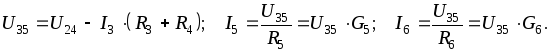
Указанный прием используется и в тех случаях, когда для упрощения цепи приходится прибегать к преобразованию «треугольник звезда» или «звезда треугольник». Недостаток заключается в том, что цепь приходится рассчитывать дважды – преобразованную и исходную.
При расчетах удобно
пользоваться формулой
о токах в двух параллельных пассивных ветвях.
Выведем ее на примере схемы рис. 2.1.
Напряжение 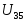 по закону Ома определяется по формуле
по закону Ома определяется по формуле
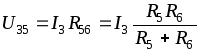
Тогда ток 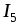 можно определить
можно определить
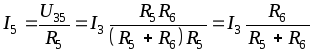 (2.2)
(2.2)
Аналогично можно определить ток
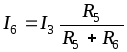 (2.3)
(2.3)
Таким образом, ток в одной из двух параллельных ветвей равен току неразветвленной части (общей ветви), умноженному на сопротивление противоположной ветви, деленному на сумму сопротивлений обеих ветвей.
Известен еще один метод расчета таких цепей – метод пропорциональных величин. Он применим к «удлиненным» цепям (цепным соединениям).
Суть этого метода
состоит в следующем: в ветви наиболее
удаленной от источника (R6)
задаются
некоторым значением тока или напряжения.
Для удобства расчетов обычно это 1А или
1В. Затем перемещаясь к началу цепи
определяют поочередно токи и напряжения
всех ветвей вплоть до ветви, содержащей
источник. Тем самым определяют какие
напряжение Uвх и ток Iвх. должен
иметь источник для того, чтобы вызвать
во всех ветвях токи и напряжения
вычисленных значений. Если ЭДС (Е)
или задающий ток (J)
с этими значениями не совпадают, то
необходимо пропорционально изменить
вычисленные значения токов и напряжений
ветвей путем умножениях их на отношение 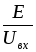 или
или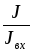 .
.
Для схемы на рис.
2.1. пусть I6 =
1. Тогда 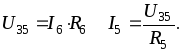
I3 можно
определить по I
закону Кирхгофа: 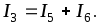
U24 определяем по II
закону Кирхгофа: 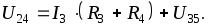
По закону Ома: 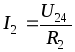 ,
поI
закону
Кирхгофа:
,
поI
закону
Кирхгофа: 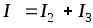 .
.
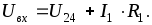
Коэффициент
пересчета определяется следующим
образом: 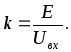 Все рассчитанные значения токов и
напряжений необходимо домножить на
коэффициентk.
Все рассчитанные значения токов и
напряжений необходимо домножить на
коэффициентk.
studfile.net
Расчет линейных электрических цепей постоянного тока
Расчет неразветвленных цепей
Основой расчета одноконтурных (неразветвленных) электрических цепей, содержащих источники обоих видов и потребители, служат рассмотренные ранее законы Ома и Кирхгофа.
Если в цепи нет источников тока, а параметры потребителей (R) и источников напряжения (Е) заданы, то задача обычно состоит в определении тока контура. Положительное направление искомого тока выбирается произвольно и составляется уравнение:
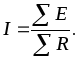 (2.1)
(2.1)
При этом необходимо помнить, что со знаком «+» берутся ЭДС источников, которые действуют в направлении выбранного тока. Истинное направление совпадает с выбранным, если в результате расчета ток оказывается положительной величиной, и противоположно выбранному, если ток оказывается отрицательным.
Если в цепи, кроме
потребителе (R)
и источников ЭДС (E),
имеется источник тока (J),
то задача обычно сводится к определению
напряжения на источнике тока UJ,
т.к. ток контура I совпадает
с заданным током источника J. Положительная полярность UJ выбирается
произвольно, но предпочтительно у острия
стрелки ставить знак «+» (такой полярности
соответствует формула: 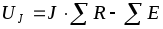 ).
Истинная полярностьUJ совпадает
с выбранной, если при расчете UJ выражается
положительным числом, и противоположна
выбранной, если UJ<
0. Искомое
падение напряжения на источнике тока UJ при отсутствии источников ЭДС определяется
по формуле
).
Истинная полярностьUJ совпадает
с выбранной, если при расчете UJ выражается
положительным числом, и противоположна
выбранной, если UJ<
0. Искомое
падение напряжения на источнике тока UJ при отсутствии источников ЭДС определяется
по формуле 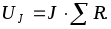 .
.
Расчет разветвленных цепей с одним источником
Разветвленную цепь с одним источником обычно упрощают, преобразуя в неразветвленную (рис. 2.1.), и решают методами, изложенными выше. Основная проблема состоит в нахождении токов и напряжений ветвей исходной схемы, поскольку в результате преобразования такие ветви не сохраняются.
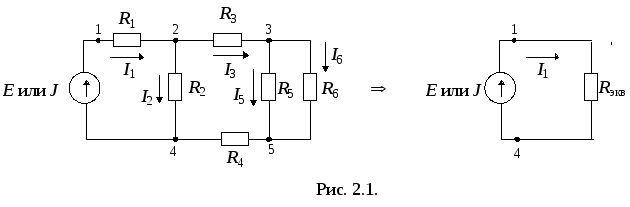
Для определения токов и напряжений в схеме рис. 2.1. сначала определяется Rэкв смешанного соединения потребителей относительно зажимов источника (точки 1 и 4 на рис. 2.1.). Затем, если цепь питается источником напряжения, то определяется ток по формуле:
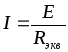
Если цепь питается источником тока, то определяется напряжение
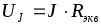
Порядок дальнейшего расчета одинаков для обоих случаев, т.к. известны E или UJ и I или J неразветвленной части схемы. Рассмотрим порядок расчета для представленной на рис. 2.1 цепи.
Ток в потребителе R1 совпадает с найденным током неразветвленной
части I, а напряжение 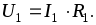
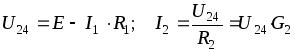 .
.
Ток I3 определяется
по закону Кирхгофа: 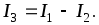
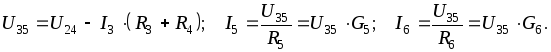
Указанный прием используется и в тех случаях, когда для упрощения цепи приходится прибегать к преобразованию «треугольник звезда» или «звезда треугольник». Недостаток заключается в том, что цепь приходится рассчитывать дважды – преобразованную и исходную.
При расчетах удобно
пользоваться формулой
о токах в двух параллельных пассивных ветвях.
Выведем ее на примере схемы рис. 2.1.
Напряжение 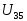 по закону Ома определяется по формуле
по закону Ома определяется по формуле

Тогда ток 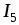 можно определить
можно определить
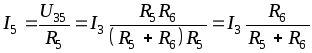 (2.2)
(2.2)
Аналогично можно определить ток
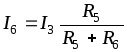 (2.3)
(2.3)
Таким образом, ток в одной из двух параллельных ветвей равен току неразветвленной части (общей ветви), умноженному на сопротивление противоположной ветви, деленному на сумму сопротивлений обеих ветвей.
Известен еще один метод расчета таких цепей – метод пропорциональных величин. Он применим к «удлиненным» цепям (цепным соединениям).
Суть этого метода
состоит в следующем: в ветви наиболее
удаленной от источника (R6)
задаются
некоторым значением тока или напряжения.
Для удобства расчетов обычно это 1А или
1В. Затем перемещаясь к началу цепи
определяют поочередно токи и напряжения
всех ветвей вплоть до ветви, содержащей
источник. Тем самым определяют какие
напряжение Uвх и ток Iвх. должен
иметь источник для того, чтобы вызвать
во всех ветвях токи и напряжения
вычисленных значений. Если ЭДС (Е)
или задающий ток (J)
с этими значениями не совпадают, то
необходимо пропорционально изменить
вычисленные значения токов и напряжений
ветвей путем умножениях их на отношение 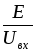 или
или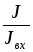 .
.
Для схемы на рис.
2.1. пусть I6 =
1. Тогда 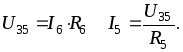
I3 можно
определить по I
закону Кирхгофа: 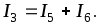
U24 определяем по II
закону Кирхгофа: 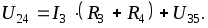
По закону Ома: 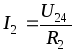 ,
поI
закону
Кирхгофа:
,
поI
закону
Кирхгофа: 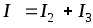 .
.

Коэффициент
пересчета определяется следующим
образом: 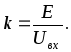 Все рассчитанные значения токов и
напряжений необходимо домножить на
коэффициентk.
Все рассчитанные значения токов и
напряжений необходимо домножить на
коэффициентk.
studfile.net
Лабораторная работа 5 разветвленная нелинейная цепь постоянного тока
Цель работы: экспериментальное получение вольтамперных характеристик нелинейных резистивных элементов, графический расчет разветвленной нелинейной электрической цепи постоянного тока и экспериментальная проверка результатов расчетов.
Оборудование: лабораторный стенд, соединительные провода, лампа накаливания А12 – 1,2 W2*4,6d, резистор 2 Вт 100 Ом, потенциометр ППБ-3А-150 Ом, нелинейный элемент.
Порядок выполнения работы
Ознакомиться с лабораторной установкой (источник питания, функциональный генератор, измеритель мощности, мультиметр, цифровые амперметры РА1…РА4, наборное поле и минимодули резисторов).
Собрать электрическую цепь для снятия вольтамперных характеристик элементов цепи (рис. 1) и предъявить ее для проверки преподавателю. В качестве регулируемого источника постоянного напряжения использовать минимодуль потенциометра RP1. В качестве амперметра использовать цифровой амперметр в режиме измерения постоянного тока. В качестве вольтметра использовать стрелочный прибор.
Обратить внимание на полярность напряжения на нелинейном элементе R1.
Предъявить схему для проверки преподавателю.
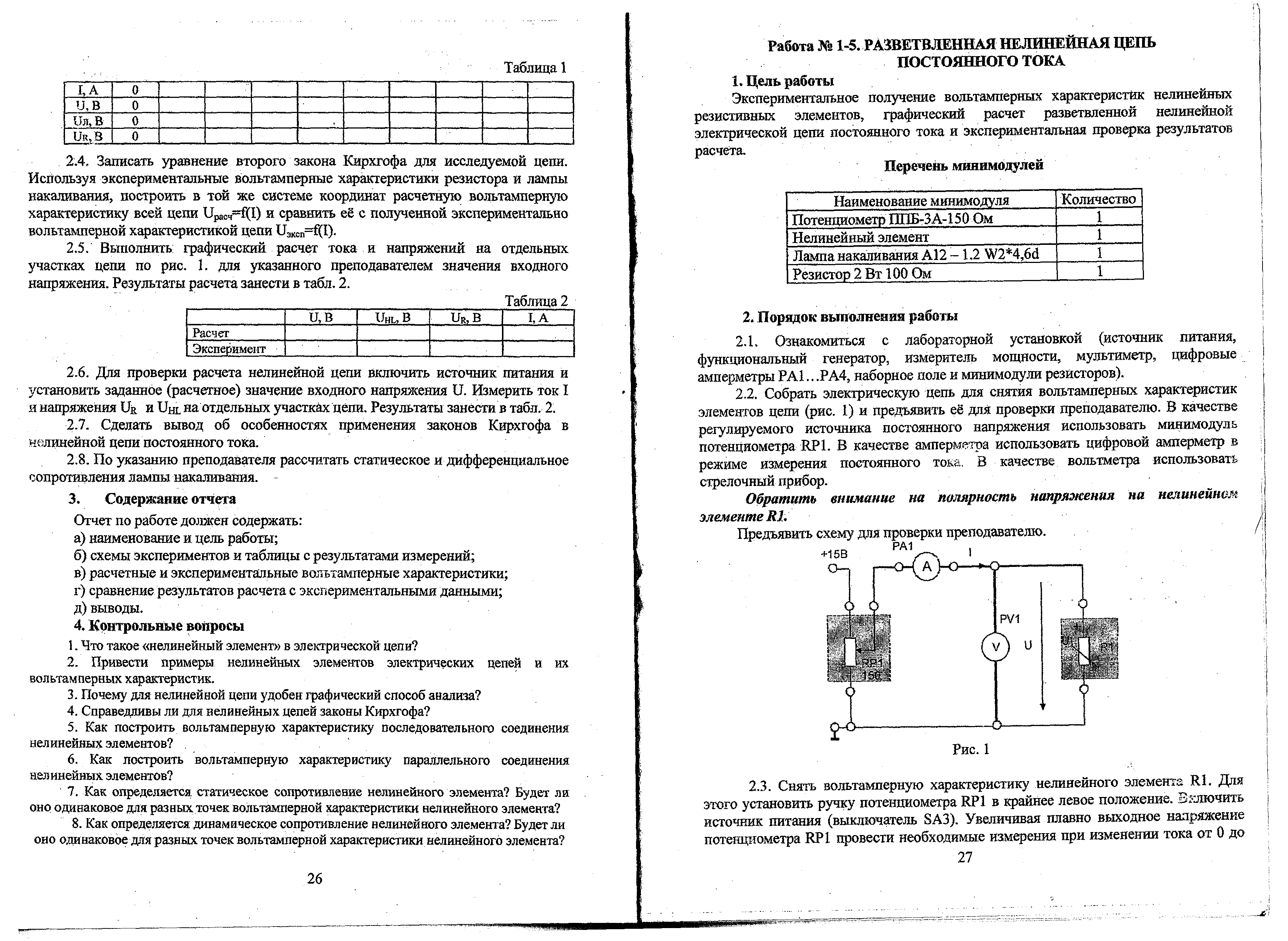
Рис. 1
Снять вольтамперную характеристику нелинейного элемента R1. Для этого установить ручку потенциометра RP1 в крайнее левое положение. Включить источник питания (выключатель SA3). Увеличивая плавно выходное напряжение потенциометра RP1 провести необходимые измерения при изменении тока от 0 до 80…100 мА. Результаты измерений занести в табл. 1. Выключить электропитание стенда. Построить вольтамперную характеристику нелинейного элемента.
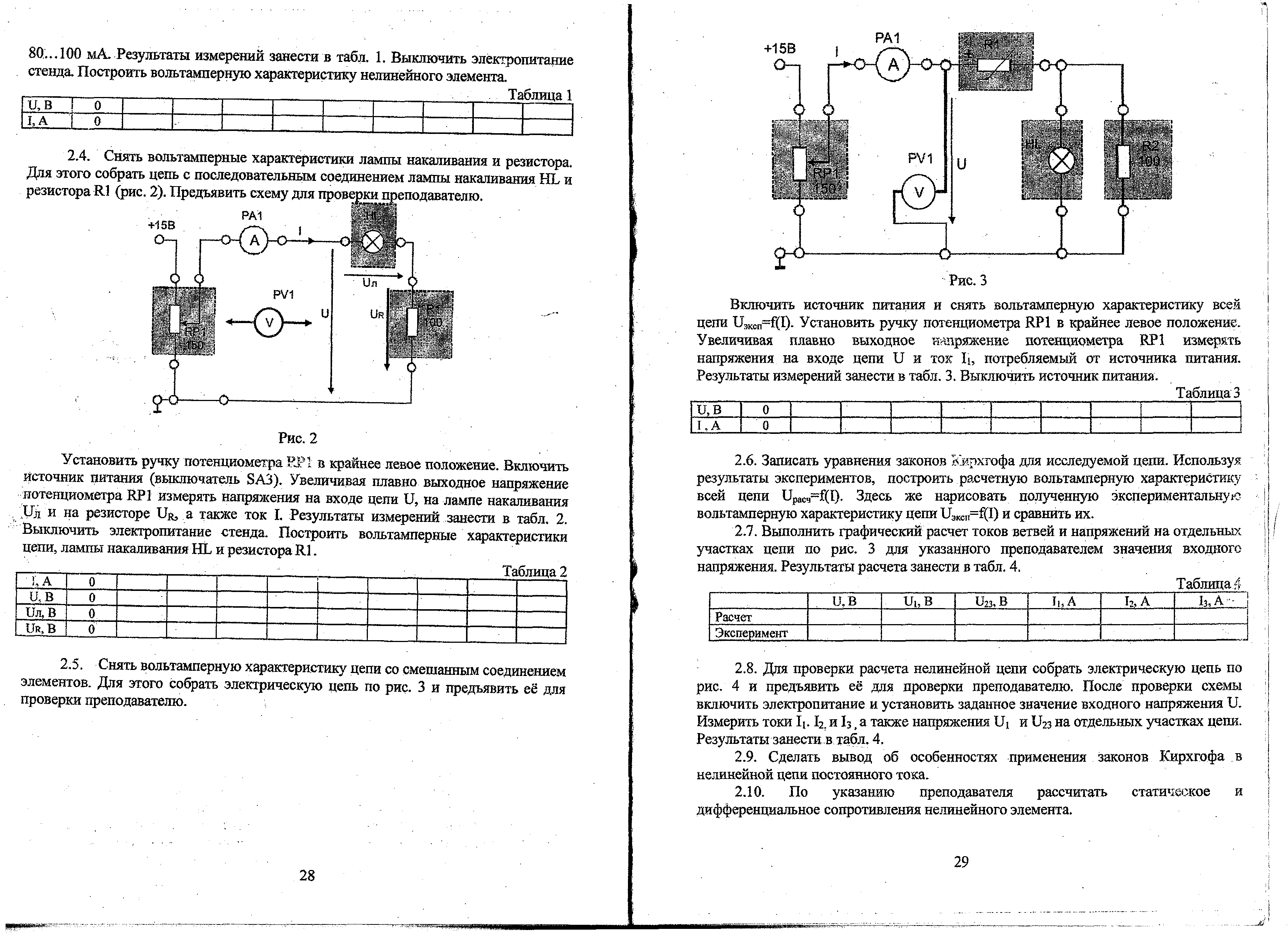
Рис. 2
Таблица 1
Снять вольтамперные характеристики лампы накаливания и резистора. Для этого собрать цепь с последовательным соединением лампы накаливания HL и резистора R1 (рис. 2). Предъявить схему для проверки преподавателю.
Установить ручку потенциометра RP1 в крайнее левое положение. Включить источник питания (выключатель SA3). Увеличивая плавно выходное напряжение потенциометра RP1 измерять напряжение на выходе цепи U, на лампе накаливания UЛ и на резисторе UR, а также ток I. Результаты измерений занести в табл. 2. Выключить электропитание стенда. Построить вольтамперные характеристики цепи, лампы накаливания HL и резистора R1.
Таблица 2
I, А | 0 | |||||||||
U, В | 0 | |||||||||
UЛ, В | 0 | |||||||||
UR, В | 0 |
Снять вольтамперную характеристику цепи со смешанным соединением элементов. Для этого собрать электрическую цепь по рис. 3 и предъявить ее для проверки преподавателю.
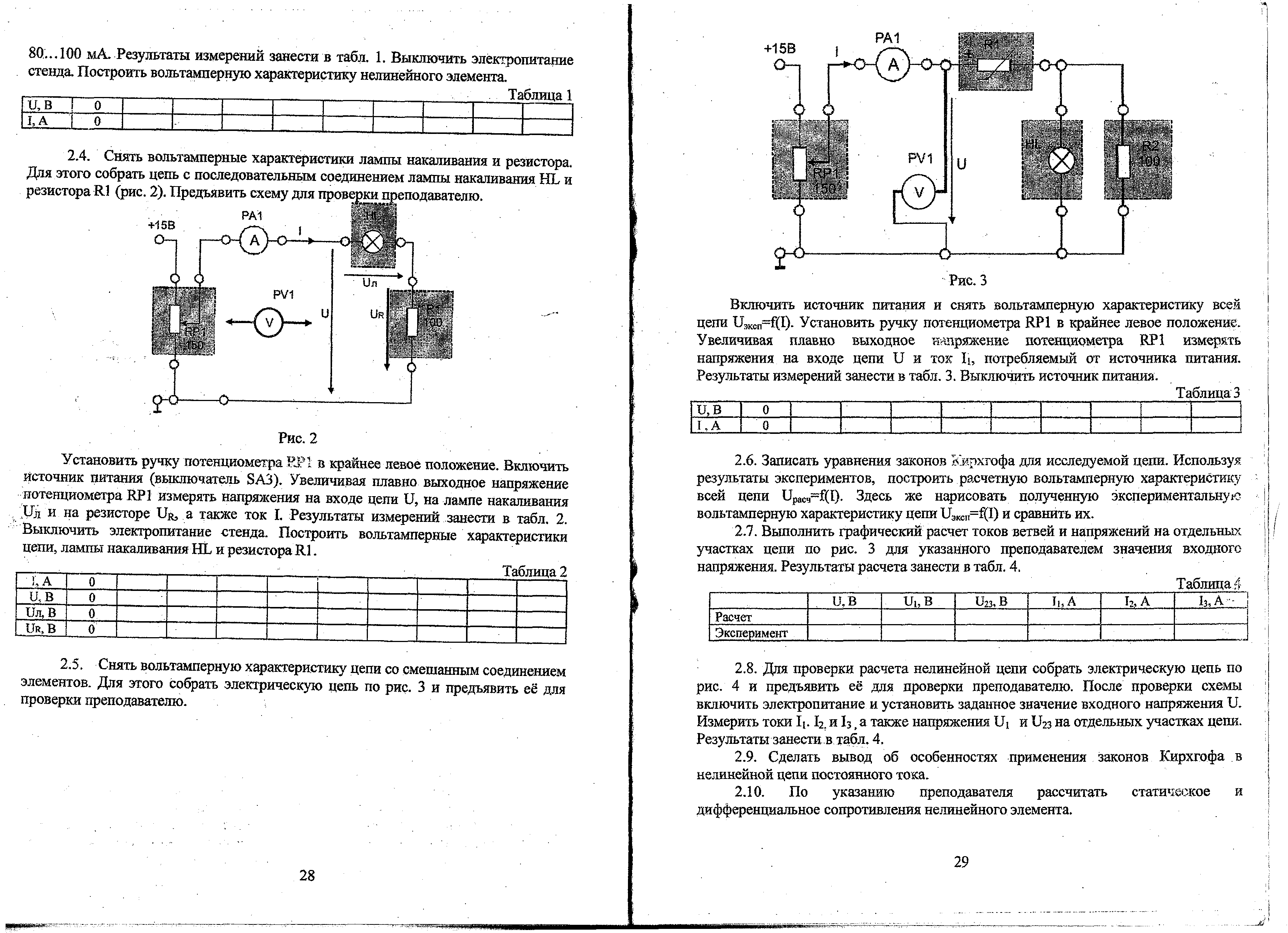
Рис. 3
Включить источник питания и снять вольтамперную характеристику всей цепи Uэксп = f (I). Установить ручку потенциометра RP1 в крайнее левое положение. Увеличивая плавно выходное напряжение потенциометра RP1 измерять напряжения на входе цепи U и ток I1, потребляемый от источника питания. Результаты измерений занести в табл. 3. Выключить питание источника.
Таблица 3
Записать уравнения законов Кирхгофа для исследуемой цепи. Используя результаты экспериментов, построить расчетную вольтамперную характеристику всей цепи Uрасч = f (I). Здесь же нарисовать полученную экспериментальную вольтамперную характеристику цепи Uэксп = f (I) и сравнить их.
Выполнить графический расчет токов ветвей и напряжений на отдельных участках цепи по рис. 3 для указанного преподавателем значения входного напряжения. Результаты расчета занести в табл. 4.
Таблица 4
U, В | U1, В | U23, В | I1, А | I2, А | I3, А | |
Расчет | ||||||
Эксперимент |
Для проверки расчета нелинейно цепи собрать электрическую цепь по рис. 4 и предъявить ее для проверки преподавателю. После проверки схемы включить электропитание и установить заданное значение входного напряжения U. Измерить токи I1, I2 и I3, а также напряжения U1 и U23 на отдельных участках цепи. Результаты занести в табл. 4.
Сделать выводы об особенностях применения законов Кирхгофа в нелинейной цепи постоянного тока.
По указанию преподавателя рассчитать статическое и дифференциальное сопротивления нелинейного элемента.
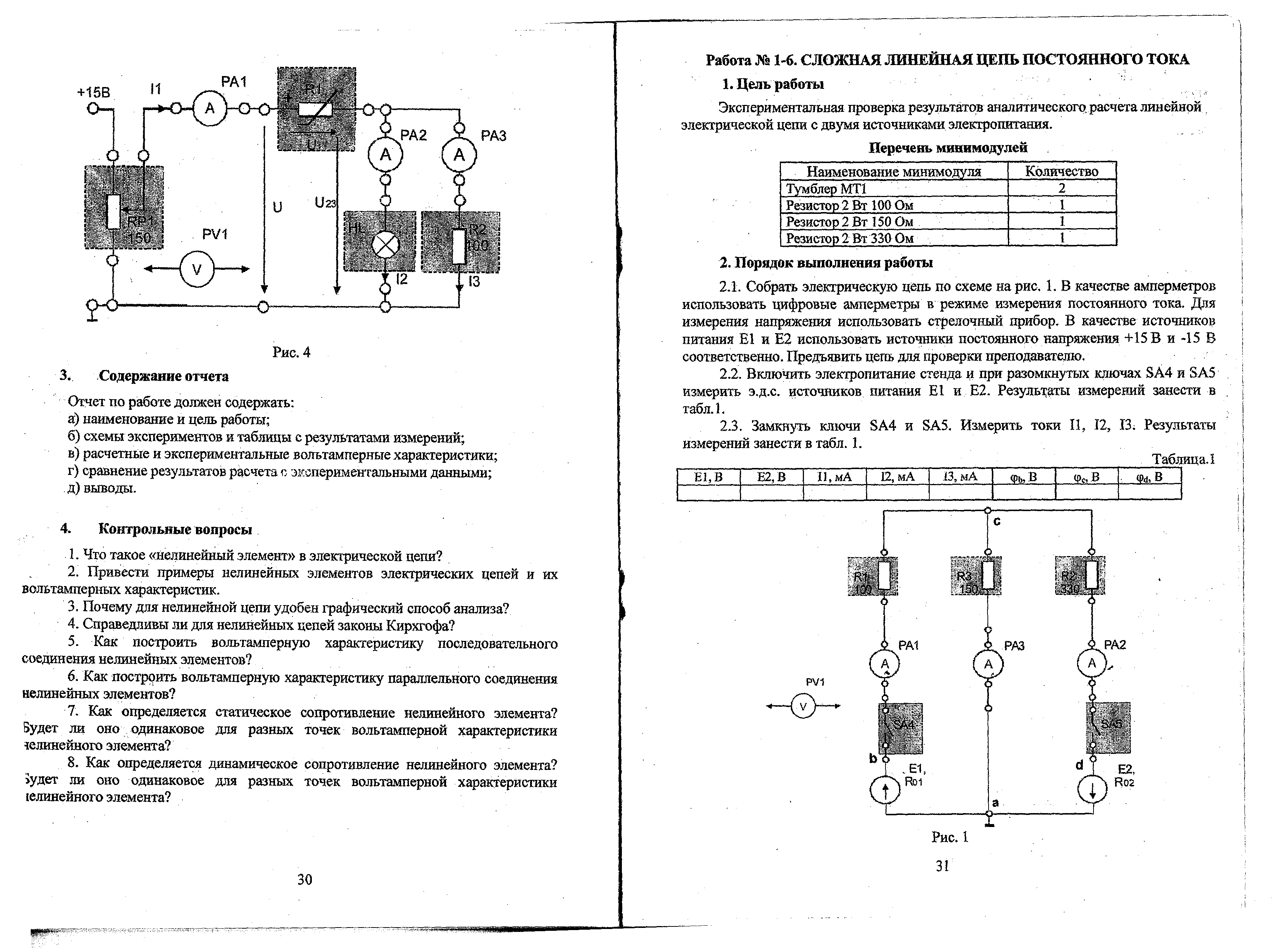
Рис. 4
Содержание отчета:
Наименование работы и цель работы.
Схемы экспериментов и таблицы полученных экспериментальных данных.
Расчетные и экспериментальные вольтамперные характеристики.
Сравнение результатов расчета с экспериментальными данными.
Выводы по работе.
Контрольные вопросы:
Что такое «нелинейный элемент» в электрической цепи?
Привести примеры нелинейных элементов электрических цепей и их вольтамперных характеристик.
Почему для нелинейной цепи удобен графический способ анализа?
Справедливы ли для нелинейных цепей законы Кирхгофа?
Как построить вольтамперную характеристику последовательного соединения нелинейных элементов?
Как построить вольтамперную характеристику параллельного соединения нелинейных элементов?
Как определяется статическое сопротивление нелинейного элемента? Будет ли оно одинаковое для разных точек вольтамперной характеристики нелинейного элемента?
Как определяется динамическое сопротивление нелинейного элемента? Будет ли оно одинаковое для разных точек вольтамперной характеристики нелинейного элемента?
studfile.net
Расчет разветвленной линейной электрической цепи постоянного тока
Задание 1:
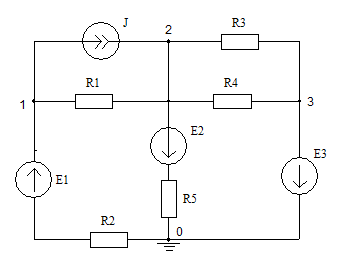
Рис. 1.1 — Исходная схема для расчёта
Дано: R1= 15 Ом; R2=12 Ом; R3=9 Ом; R4=10 Ом; R5=7 Ом; E1=9 В;
E2=7 В; E3=10 В; J=1,5 А.
Определить: токи во всех ветвях.
Решение:
1.1 Расчет токов в ветвях по законам Кирхгофа
Для упрощения дальнейших расчётов преобразуем источник тока в схеме на рис 1.1. в источник Э.Д.С.
Источник тока (рис.1.2 а) преобразуется в источник Э.Д.С (рис.1.2 б), где R5 − в обоих случаях остаётся одним и тем же, а Э.Д.С может быть определена как
E4 = J*R1; E4 =1,5*15 = 22,5В.
Сделав необходимые обозначения и произведя эквивалентную замену источника тока источником Э.Д.С., получим расчётную схему (рис.1.2).
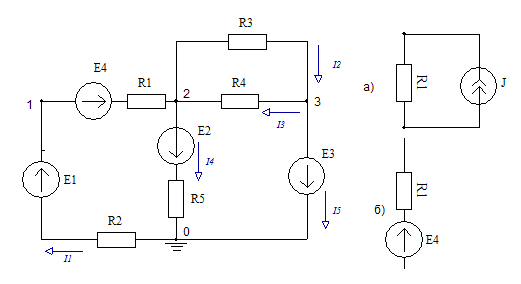
Рис 1.2 — Расчетная схема после эквивалентной замены источника тока источником Э.Д.С.
2. Произвольно выбираем и обозначим на расчетной схеме (рис. 1.2) положительное направление токов в ветвях, направление обхода контуров выбираем по часовой стрелке.
3. Определим количество уравнений, которые необходимо составить по первому и второму закону Кирхгофа.
По первому закону Кирхгофа количество уравнений определяем из выражения:
| (1.1) | |
где |
| |
Узлов
в схеме – 3
(0,
2, 3), 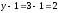 .
.
Значит, необходимо по первому закону Кирхгофа составить два уравнения. При составлении уравнений учитываем, что положительными считаются токи, направленные к узлу.
Запишем уравнения по первому закону Кирхгофа для узлов 2, 3:
узел 2: I1 — I2 + I3 — I4=0; узел 3: I2 – I3 – I5=0. | (1.2) |
По второму закону Кирхгофа количество уравнений определяем из выражения:
| (1.1) | |
где |
| |
Ветвей
в схеме — 5 , ветвей содержащих источники
тока — 0, 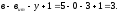
Значит, для рассмотренной цепи, необходимо по второму закону Кирхгофа составить три уравнения.
При составлении уравнений учитываем, падение напряжения считается положительным, если направление тока в сопротивлении совпадает с направлением обхода контура; ЭДС считается положительной, если она действует по направлению обхода контура.
Запишем уравнения по второму закону Кирхгофа:
Для контура I: I1(R1 + R2) + I4R5 = E1 + E2 + E4; Для контура II: I2R3 + I3R4 =0; Для контура III: -I3R4 – I4R5 = – E2 + E3. | (1.2) |
По первому и второму законам Кирхгофа записаны пять уравнений с пятью неизвестными токами и при решении этой системы уравнений, можно определить все неизвестные токи.
| (1.3) |
Решение этой системы уравнений достаточно трудоемко, поэтому решим её в программе MathCAD 7.0 pro
Для решения системы уравнений в программе MathCAD используем встроенный оператор Given, Find.
1. Вводим исходные значения.
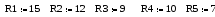

2. Вводим первичное приближение для неизвестных системы уравнений.
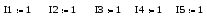
3. Вводим оператор Given.
4. Вводим систему уравнений.

5. Решим систему уравнений, используя, оператор Find.

6. Запишем ответ, полученный в результате вычислений.
Ответ: 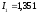 А;
А;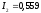 А;
А;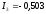 А;
А;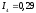 А;
А;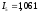 А.
А.
Задание 2а: Определить токи ветвей в схеме методом контурных токов, приведенной на рис. 1.3.
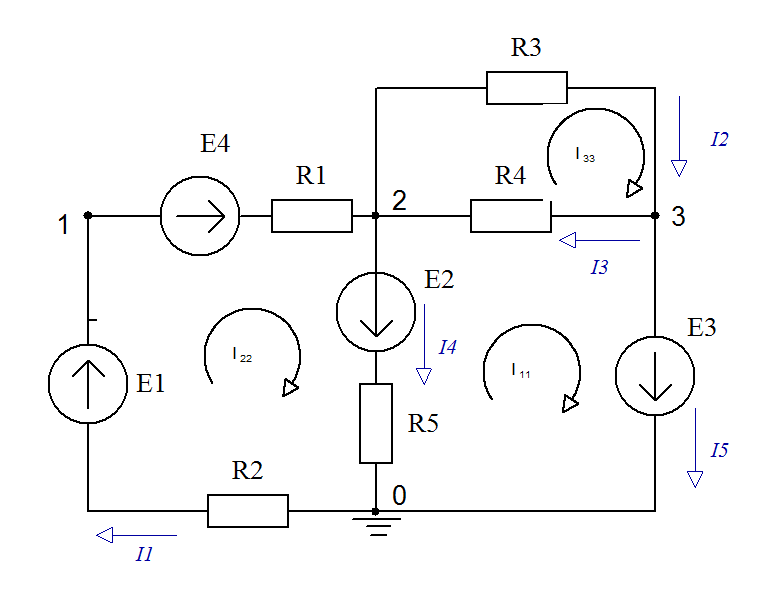
Рис. 1.3
Решение.
Выбираем произвольно направления трех контурных токов.
В общем виде составляем систему уравнений относительно трех неизвестных контурных токов:
I11R11+I22R12+I33R13 = E11;
I11R21+I22R22+I33R23 = E22;
I11R31+I22R32+I33R33 = E33;
где: R11 = R4+R5; R11 = 17 Ом;
R22 = R1+R2+R5; R22 = 34 Ом;
R33 = R3+R4; R33 = 19 Ом;
R12 = R21 = -R5 = 7 Ом; R13 = R31 = -R4=-10 Ом;
R32 = R23 = 0 Ом;
E11 =E3 -E2=3 В;
E22 =E1 +E2+E4 = 38,5В;
E33 = 0 В.
После подстановки система уравнений принимает вид:
I1117–I227-I3310 = 3;
I11(–7)+I2234= 38,5;
-I1110 +I3319 = 0;
Решим её в программе MathCAD 7.0 pro. Для решения системы уравнений в программе MathCAD используем встроенный оператор Given, Find.
По правилу Крамера:
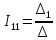 ;
; 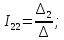
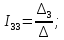
где:
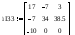



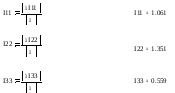
Получили: I11 = 1,061 A; I22 = 1,351 A; I33 = 0,559 A.
В итоге токи ветвей:
I1 = I22; I1 = 0.839 A;
I2 = I33; I2 = 0,559 A;
I3 = I33 – I11; I3 = -0,502 A;
I4 = I22 – I11; I4 = 0,29 A;
I5 = I11; I5 = 1,061 A;
Знак «минус» у тока I3указывает на то, что в действительности эти токи имеют направления, противоположные указанным на схеме.
Задание 2б: Определить токи ветвей в схеме методом узловых потенциалов.
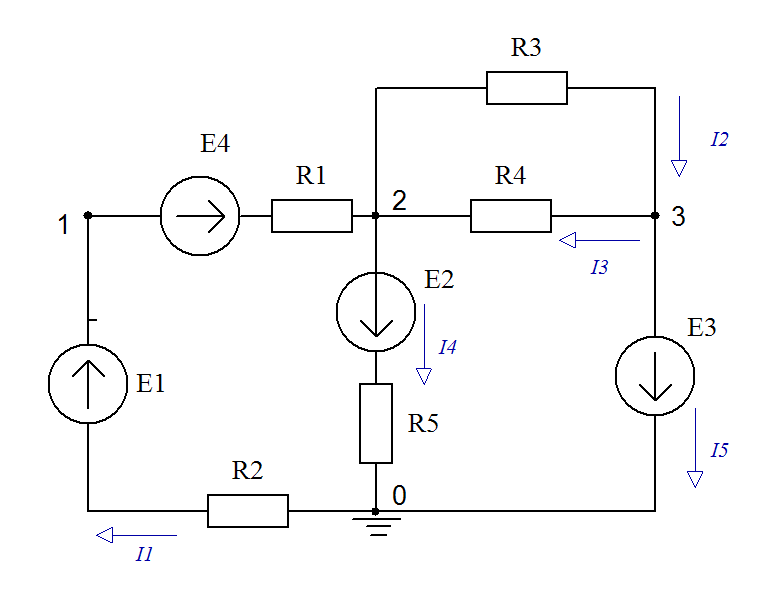
Рис. 1.4
Решение.
Заземляем узел 0 (φ0 = 0). Кроме того, ветвь между узлами 3 и 0 содержит только источник ЭДС, следовательно, независимо от величины протекающего тока I5 величина φ3 также известна: φ3 = —E2 (направление E2 от узла 3). Таким образом, в задаче неизвестным является потенциал одного узла: φ2 . Достаточно составить одно уравнение, где должны быть учтены связи с потенциалом φ3:
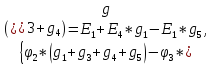
Используем Mathcad:
1. Вводим исходные значения.
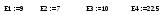

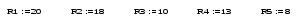
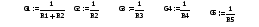
2. Вводим первичное приближение для неизвестных системы уравнений
3. Вводим оператор Given.
4. Вводим систему уравнений:
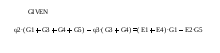
5. Решим систему уравнений, используя, оператор Find.
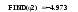
Получили: 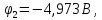
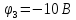 ,
,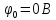
Рассчитаем токи ветвей в Mathcad, используя полученные результаты:
1. Вводим исходные значения.

2. Вводим первичное приближение для неизвестных системы уравнений
3. Вводим оператор Given.
4. Вводим систему уравнений:
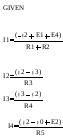
5. Решим систему уравнений, используя оператор Find.
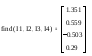
I5 найдем по первому закону Кирхгофа:
Из узла 3:
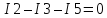
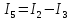
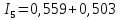
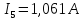
Составление баланса мощностей для схемы (Рис. 1.1)
Решение.
(E1+E4)I1+E2I4 +E3I5=I12(R1+R2) +I22R3+I32R4+I42R5
Подставляя значения E, R из данных задач, а также токи, рассчитанные любым методом, получаем:
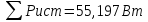
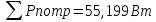
Расхождение составляет:
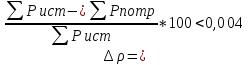
Построение потенциальной диаграммы.
Потенциальная диаграмма для замкнутого контура 4-3-a—1-2-b-4,содержащего два источника ЭДС – E1 и E3 (рис.1.5). Приравняем к нулю потенциал любой точки контура φ4 = 0.
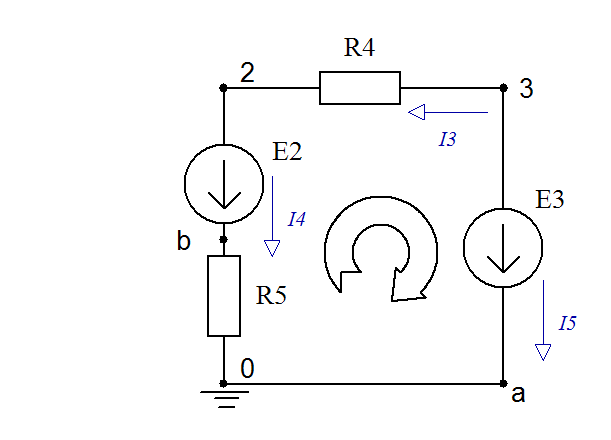
Рис. 1.5
Выберем направление обхода по часовой стрелке, составим уравнения для определения потенциалов каждой точки контура, подставим заданные значения токов, сопротивлений и ЭДС и тогда получим:
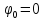 ,
,
 ,
,
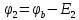 ,
,
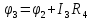 ,
,
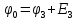 .
.
После
вычислений получили: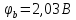 ,
,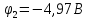 ,
,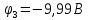 ,
,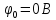 .
.
По оси ординат откладываем величину потенциала. По оси абсцисс–сопротивления участка контура в нарастающем порядке.
Перед
построением диаграммы выбираем масштабы
потенциалов и сопротивлений: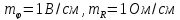 .
Построим потенциальную диаграмму с
помощьюMathcad:
.
Построим потенциальную диаграмму с
помощьюMathcad:
Вводим значения

Составим матрицы:
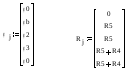
Построим потенциальную диаграмму:

Составим таблицу результатов:
Метод | I1 | I2 | I3 | I4 | I5 |
Законы Кирхгофа | 1,351 | 0,559 | -0,502 | 0,29 | 1,061 |
М. контурных токов | 1,351 | 0,559 | -0,502 | 0,29 | 1,061 |
М. узловых потенциалов | 1,351 | 0,559 | -0,502 | 0,29 | 1,061 |
Вывод: Независимо от метода решения ответы сходятся.
РАСЧЕТ ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА
studfile.net
Лабораторная работа №1 Исследование линейной электрической цепи постоянного тока
Цель работы:
Закрепить на практике важнейшие положения теории цепей постоянного тока.
Экспериментально подтвердить справедливость основных законов теории электрических цепей.
Приобрести навыки самостоятельного исследования линейных разветвленных цепей постоянного тока.
1. Теоретическое введение
1.1. Основные понятия и определения
При подготовке к работе и оформлении отчета рекомендуется использовать следующие методические указания:
Котов В.Л. Линейные электрические цепи постоянного и однофазного переменного токов. Иваново, 1988.
Котов В.Л. Расчет линейных разветвленных цепей постоянного и синусоидального тока. Иваново, 1983.
Цепи постоянного тока являются важной частью электрооборудования химических производств. Например, постоянный ток широко применяется для питания ванн гальванического покрытия, зарядных устройств для аккумуляторов, двигателей постоянного тока, устройств сигнализации и связи.
Под постоянным током понимают электрический ток, не изменяющийся во времени.
Электрической цепью называется связанная совокупность источников электроэнергии, ее потребителей и соединительных проводов.
Отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определенную функцию, называется элементом электрической цепи. Основными элементами являются источники и приемники электроэнергии, соединительные провода, измерительные приборы, коммутационная и защитная аппаратура.
В источниках электроэнергии различные виды энергии, например, химическая (гальванические элементы), механическая (электромеханические генераторы), тепловая (термопары), световая (солнечные батареи) преобразуются в электрическую. Важнейшим параметром источника электроэнергии является его электродвижущая сила ЭДС (Е).
В приемниках электрической энергии происходит обратное преобразование — электрическая энергия преобразуется в другие виды энергии, например, в химическую, механическую, тепловую, световую.
Электрические цепи классифицируются по нескольким признакам.
По виду тока делят на цепи постоянного и переменного тока.
По характеру параметров переменных цепи разделяют на линейные и нелинейные. К линейным относят цепи, у которых электрическое сопротивление R каждого участка не зависит от значений и направлений тока и напряжения.
Классификация цепей по сложности. Цепи бывают простые и сложные. К простым относят те цепи, все элементы которых соединены последовательно. Во всех элементах протекает один и тот же ток. К сложным цепям относят цепи с разветвлениями. Различают разветвленные цепи с одним источником энергии и с несколькими источниками.
Ветвь электрической цепи— участок, элементы которого соединены последовательно. Ток в элементах один и тот же.
Узел электрической цепи— точка соединения не менее чем 3-х ветвей.
Контур— любой путь вдоль ветвей электрической цепи, начинающийся и заканчивающийся в одной и той же точке.
Двухполюсник— часть электрической цепи с двумя выделенными выводами.
Четырехполюсник— часть электрической цепи, имеющая четыре внешних вывода (две пары).
Участки электрической цепи делятся на пассивные и активные. Участок электрической цепи, содержащий источник электрической энергии, называется активным, не содержащий — пассивным.
Величина, характеризующая противодействие проводящей среды движению электрических зарядов, т.е. току, называется электрическим сопротивлением R. Элемент электрической цепи, параметром которого является его электрическое сопротивление R, называется резистором. Величина, обратная сопротивлению, называется проводимостью G.
Закон Ома. Для пассивных участков электрической цепи закон Ома имеет вид:
| (1) |
Напряжение на пассивном участке цепи U и равное ему произведение IR часто называют падением напряжения.
Внутреннее сопротивление источника. У реального источника энергии два параметра: ЭДС Е и внутреннее сопротивление Rо, которое на схемах замещения показывается отдельным элементом. Если источник не подключен к внешней цепи, то напряжение на его выводах числено равно ЭДС (напряжение холостого хода). Напряжение U на выводах нагруженного источника меньше ЭДС
Источник, внутренним сопротивлением которого можно пренебречь, называется идеальным источником ЭДС.
studfile.net

 ,
,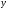 —
число узлов.
—
число узлов.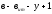 ,
, —
число ветвей;
—
число ветвей; 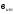 — число ветвей содержащих источники
тока.
— число ветвей содержащих источники
тока.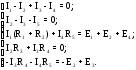
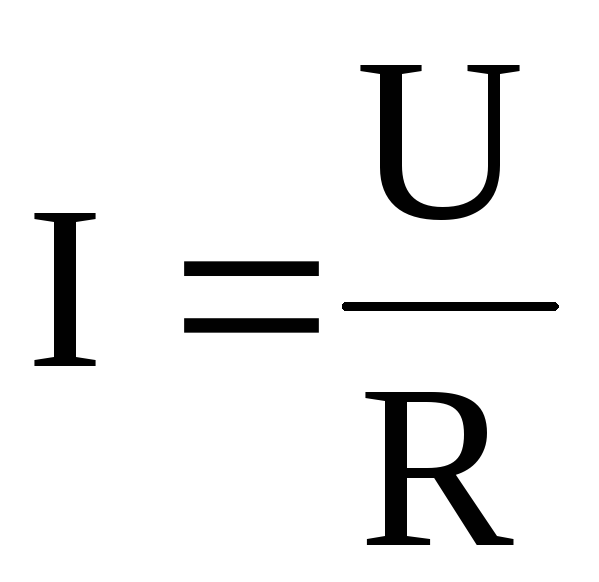 .
.