§10. Разветвленные электрические цепи. Правила Кирхгофа

Расчет сложных (разветвленных) цепей постоянного тока заключается в отыскании по заданным сопротивлениям участков цепи и приложенных к ним Э.Д.С. сил токов в каждом участке. Для решения этой задачи применяются правила Г.Р. Кирхгофа (1847 г.).

Любая разветвленная цепь состоит из совокупности однородных и неоднородных участков цепи, электрическое соединение которых происходит в узлах. Узлом в разветвленной цепи называется точка, в которой имеется более двух возможных направлений тока (рис. 10.1). В узле сходится более двух проводников.

Р

I₃

I₂

I₁, I

₂, I₃

ассмотрим узелA{I₁,I₂,I₃} (рис. 10.1) для трех токов. Условие стационарности токов (6.9) в узле А позволяют записать уравнение непрерывности в интегральной форме.

I₁

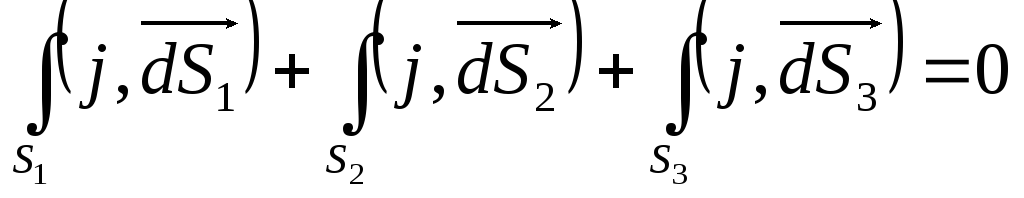
или 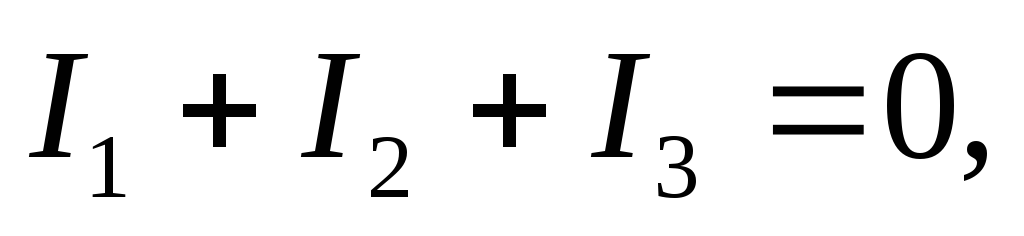(10.1)

где ток берется со знаком плюс, если вытекает из узла, и со знаком минус, если приходит к узлу (правило знаков).

Обобщая результат 10.1 на произвольный узел, сформулируем 1-е правило Кирхгофа: алгебраическая сумма токов в узле разветвленной цепи постоянного тока равна 0:

(10.2)

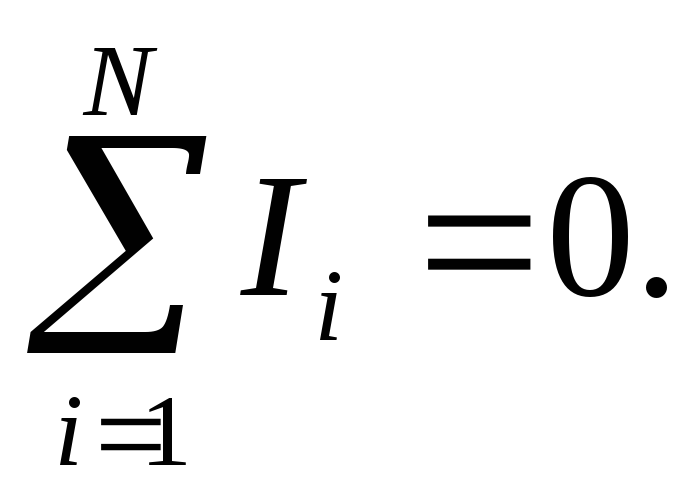
Узлы, образованные одними и теми же токами, называются эквивалентными.

II-е правило Кирхгофа.

Р

I₁

I₂

I₃

I₄

ассмотрим выделенный произвольный замкнутый контур некоторой разветвленной цепи (рис. 10.2), состоящей из 4-х участков между четырьмя узлами разветвленной цепи. Для каждого участка применим закон Ома для неоднородного участка цепи (9.5)

₄ — ₁ +₁ = I₁(R₁ + r₁)

₁ — ₂ + ₂= I₂(R₂ + r₂)

₂ — ₃ + ₃= I₃(R₃ + r₃)

₃ — ₄ + ₄= I₄(R₄ + r₄)

Складывая эти равенства, получим

₁ + ₂ + ₃ + ₄ = I₁(R₁ + r₁) + I₂(R₂ + r₂) + I

₃(R₃ + r₃) + I₄(R₄ + r₄).

В общем случае при произвольном количестве замкнутых контуров разветвленной цепи второе правило Кирхгофа позволяет получить систему линейных уравнений:

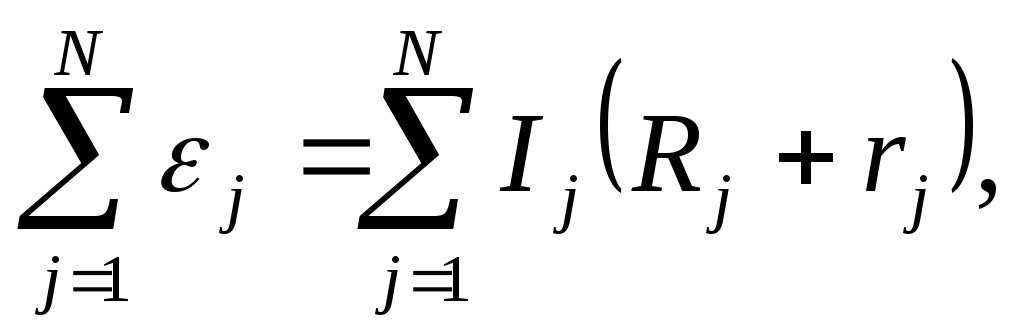(10.3)

где r_j, _j – внутреннее сопротивление и э.д.с., включенная в j — участок контура,

I_j – ток на j — участке контура, R_j – сопротивление j — участка контура.

При составлении уравнений на основе второго правила Кирхгофа необходимо поступать следующим образом:

1. Произвольно выбрать направление токов во всех участках разветвленной цепи, обозначив их стрелками. Если вычисление покажет, что ток положителен, то его направление совпадает с истинным. Если отрицателен, то истинное направление противоположно выбранному.

2. Выбрав произвольный замкнутый контур разветвленной цепи, все его участки следует обойти в одном направлении. Если это направление совпадает с выбранным направлением тока, то падение напряжения I_j R_j и I_j r_j берется со знаком плюс. Если же эти направления противоположны, то оно берется со знаком минус. Если при обходе контура источник тока проходится от отрицательного полюса к положительному, то его э.д.с. следует считать положительной; в противоположном случае отрицательной.

Число уравнений, составляемых по первому закону Кирхгофа, должно быть на 1 меньше числа узлов. Число уравнений, составляемых по второму закону Кирхгофа, должно быть на 1 меньше числа замкнутых контуров.

§11. Электрический ток в газах

В нормальном состоянии газы, в том числе и пары металлов, не проводят электрический ток, так как состоят из электрически нейтральных атомов. Проводящим электрический ток может быть только ионизированный газ, то есть газ, содержащий не только нейтральные атомы или молекулы, но и положительные и отрицательные ионы и электроны. Ионизация газа может возникать под действием высоких температур, рентгеновских и ультрафиолетовых лучей, излучений радиоактивных элементов, космических лучей, в результате столкновений атомов газа с электронами и другими быстрыми частицами и т.д. Во всех этих случаях происходит вырывание из электронной оболочки атома или молекулы газа одного или нескольких электронов и в газе возникают свободные носители заряда: электроны и положительно заряженные ионы. Внешнее электрическое поле в ионизированном газе вызывает дрейфовый ток свободных носителей заряда электронов и ионов. Прохождение электрического тока через ионизированную газовую среду сопровождается изменением состояния газа. Многообразие условий, определяющих исходное состояние газа (состав, давление и т.д.), внешних воздействий на газ, материалов, форм и расположения электродов, конфигураций возникающего в газе электрического поля и т.п. приводит к тому, что существует множество видов электрического разряда (тока) в газах. Законы электрического разряда в газах значительно сложнее, чем законы электрического тока в металлах и электролитах. Электрический разряд в газах лишь при очень малой разности потенциалов, приложенной извне, подчиняется закону Ома. Как правило, вольт-амперная характеристика газового разряда имеет ярко выраженный нелинейный характер.

Ионизация газа, возникающая в результате вырывания электронов из молекул и атомов самого газа, называется объемной ионизацией. Помимо объемной ионизации существует поверхностная ионизация. При такой ионизации ионы или электроны поступают в газ со стенок сосуда, в котором он заключен, или с поверхности тел, вносимых в газ. Например, источниками электронов могут быть раскаленные тела (термоэлектронная эмиссия).

Наряду с ионизацией в ионизированном газе имеет место соединение положительных и отрицательных ионов или электронов между собой с образованием нейтральных молекул и атомов. Этот процесс называется рекомбинацией. В результате рекомбинации проводимость газов постепенно падает.

Рассмотрим динамику процесса ионизации и рекомбинации в ионизированном газе. Предполагая отсутствие дрейфа и диффузии носителей зарядов в газе, единственными процессами будут ионизация и рекомбинация. Допустим, что источник создает в единицу времени в единице объема газа q пар ионов разных знаков. Обозначим через n число пар ионов разных знаков в единице объема газа. Число рекомбинирующих ионов пропорционально n² и может быть записано в виде

n², где  — постоянная, называемая коэффициентом рекомбинации ионов разных знаков. Введенные допущения позволяют записать уравнение баланса ионов в газе в виде

(11.1)

В стационарном состоянии dn/dt=0, следовательно,

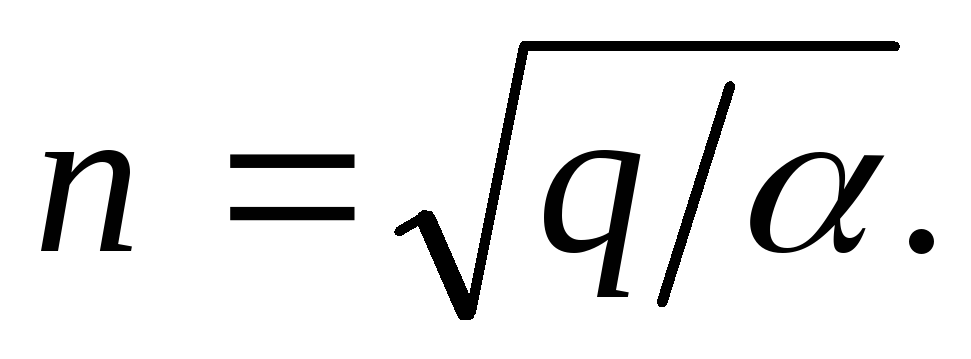(11.2)

При выключенном ионизаторе генерация ионов прекращается q=0

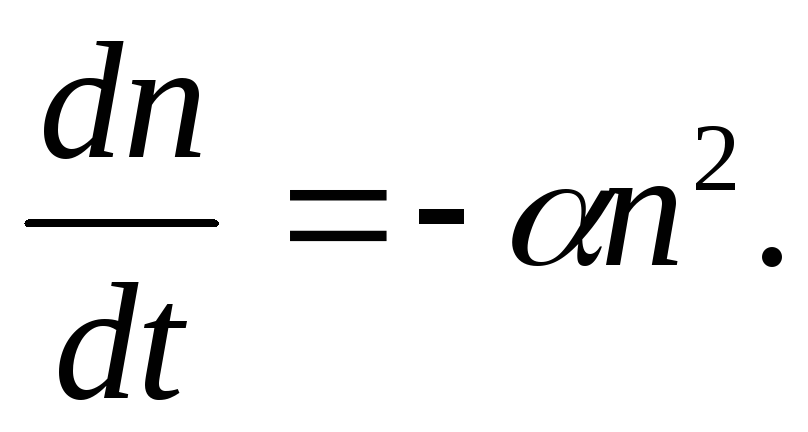
Преобразуем полученное соотношение и проинтегрируем от t = 0 до некоторого текущего значения t, которому соответствует концентрация положительных и отрицательных пар ионов n(t):

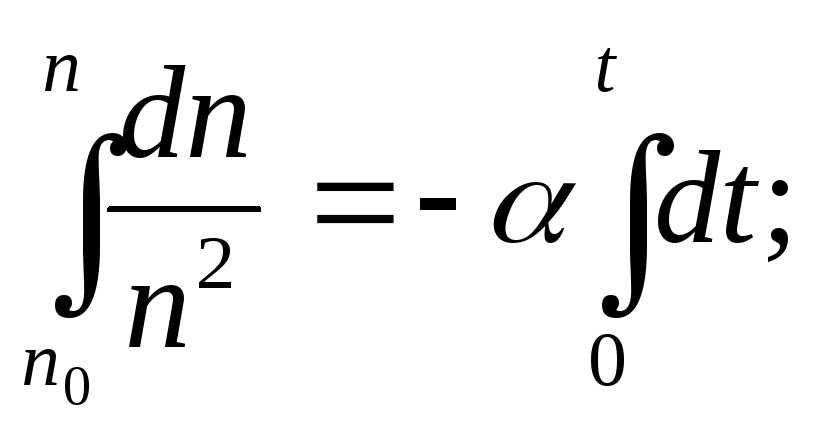
После интегрирования получим

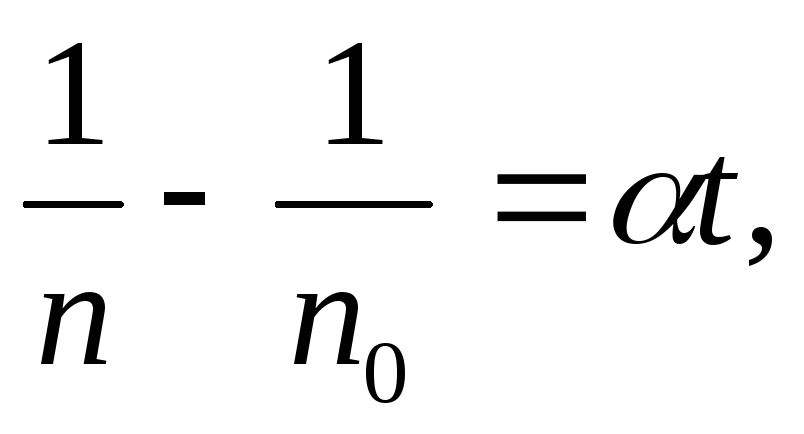(11.3)

где n₀ — концентрация пар положительных и отрицательных ионов при t=0. Время, за которое концентрация убывает в 2 раза, равно

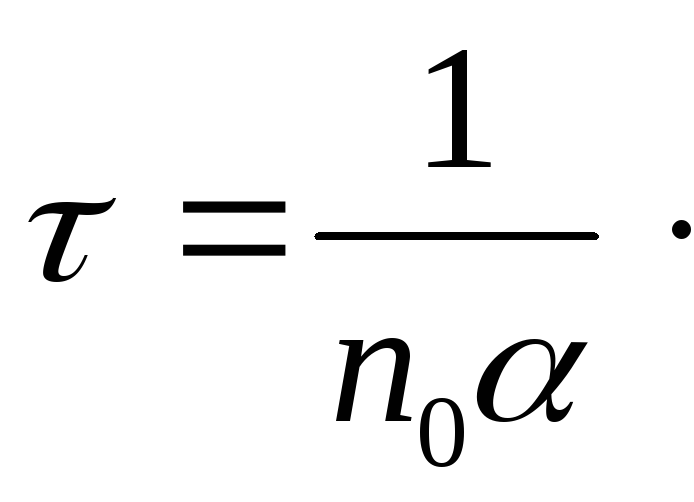(11.4)

При включении ионизатора в момент времени t=0 концентрация пар ионов равна 0. Учитывая это и тот факт, что q —n²>0, интегрирование уравнения 11.1 дает следующий результат:

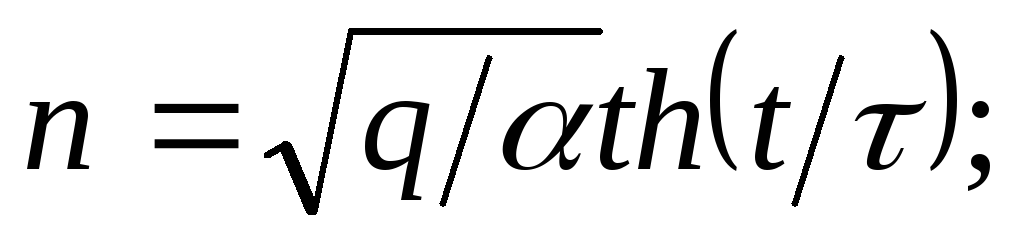(11.5)

Процесс ионизации требует затрат энергии. Минимальное значение такой энергии называется энергией ионизации атома или молекулы. В пределах отдельных периодов системы элементов Менделеева наибольшим потенциалом обладают атомы инертных газов, наименьшим – атомы щелочных металлов. Так, ионизационный потенциал атома гелия равен 24,58 В, неона 21,56 В, лития 5,39 В, натрия 5,13 В. Ионизационный потенциал, как правило, уменьшается с увеличением атомного номера элемента.

При рекомбинации положительного и отрицательного ионов потенциальная энергия уменьшается. Частично она идет на излучение электромагнитных волн, которое называется рекомбинационным излучением.

Неразветвленные и разветвленные электрические цепи

1. Курс теории электрических цепей является составной частью курса теоретических основ электротехники (ТОЭ). Это фундаментальная наука, базирующаяся на исследованиях в области электрических и магнитных явлений.

В том виде, как мы ее знаем, она возникла сравнительно недавно — в начале ХХ века, однако путь, который она прошла, был достаточно долгим и трудным. Потребовалось достаточно много творческих усилий как наших, так и зарубежных ученых, чтобы внешне разрозненные явления природы были систематизированы и выстроены в строгую теорию.

Без электрической энергии сегодня не возможно представить нашу жизнь. Она применяется по всюду и потребность в ней неуклонно возрастает. Столь широкое распространение этого вида энергии не случайно, ибо ее можно передавать на огромные расстояния от источника до потребителя. Она способна легко трансформироваться в другие виды, такие как: механическую, химическую, световую и др. При этом возможен и обратный ее переход, что подтверждает универсальность данного вида энергии.

Развитие электроэнергетики, как науки, потребовало больших усилий в области изучения электромагнитных явлений и их практического применения. Работы в этом направлении начались давно. Первый трактат по электричеству вышедший в 1753 г., принадлежит нашему великому соотечественнику М. В. Ломоносову — «Слово о явлениях воздушных, от электрической силой происходящих», посвященный теории атмосферного электричества.

Потребовалось более чем полвека, прежде чем А. Вольта изобрел свой гальванический столб. Все это позволило впервые получить реальный электрический ток.

Первые годы XIX века явились началом развития теории и практики цепей постоянного тока. В этой связи приведем хронологическую последовательность открытий, положивших начало систематическому изучению электрических и магнитных явлений.

Рассматривая хронологию развития данной науки, выделим основные ее даты.

1802 г. — В. В. Петров обнаружил и исследовал явление электрической дуги между двумя угольными электродами. Он указал на возможность ее использования для освещения, плавки и сварки металлов.

1819 г. — Эрстед обнаружил механическое воздействие электрического тока на магнитную стрелку.

1820 г. — Ампер открыл магнитные свойства соленоида с током.

1831 г. — Фарадей открыл и впервые описал явление электромагнитной индукции.

1833 г. — Э. Х. Ленц (русский академик) открыл фундаментальный принцип электродинамики — принцип электромагнитной инерции; он же в 1844 г., не зависимо от Джоуля, открыл закон о тепловом действии электрического тока.

1845 г. — Кирхгофф сформулировал основные законы для разветвленных электрических цепей, имеющие фундаментальное значение.

1876 г. — П. Н. Яблочков (русский инженер) изобрел электрическую свечу, которая положила начало электрическому освещению; он же был и автором реализации использования переменного электрического тока, а так же создал первый в мире трансформатор.

Период времени с 1800 по 1880 гг. можно считать периодом становления теории и практики цепей постоянного тока.

С открытием П. Н. Яблочковым переменных токов начался новый этап развития электротехники. Переменный ток получил исключительно широкое практическое применение благодаря изобретениям русского инженера М. О. Доливо-Добровольского.

1889 г. — М. О. Доливо-Добровольский построил первый 3-х фазный электрический двигатель и разработал все основные звенья 3-х фазной электрической цепи, он же в 1891 г. осуществил передачу электроэнергии 3-х фазным током на расстояние 175 км.

Применение переменных токов потребовало решения целого ряда теоретических и практических задач, существенно отличающихся от задач по расчету цепей постоянного тока. Важнейшим этапом здесь можно считать введение американским инженером Штейнметцем комплексного метода расчета цепей переменного тока.

Создание первых электрических машин (электрических двигателей и трансформаторов), а так же линии электропередач потребовало исследований по расчету электрических и магнитных полей, а так же их совокупности — единого электромагнитного поля.

1888 г. — Герц экспериментально доказал существование поля излучения, теоретически предсказанного Максвеллом в 1873 г. Однако сам Герц и многие другие физики не верили в возможность использования электромагнитных волн для беспроводной связи.

1895 г. — А. С. Попов (русский инженер) блестяще решил практическую задачу по передаче информации с помощью электромагнитных волн. Изобретение радиосвязи открыло новую эру в культурной жизни человечества (первые слова эфира были «Генрих Герц»).

2. Электри́ческая цепь — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение

Изображение электрической цепи с помощью условных знаков называют электрической схемой 

Электрические цепи подразделяют на неразветвленные и разветвленные. На рисунке 1 представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 2. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.

Линейные и нелинейные электрические цепи

Изображение электрической цепи с помощью условных знаков называют электрической схемой (рис. 2.1, а). Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении называют вольт-амперной характеристикой (ВАХ). По оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток. Сопротивления, ВАХ которых являются прямыми линиями (рис. 2.1, б), называют линейными, электрические цепи только с линейными сопротивлениями — линейными электрическими цепями. Сопротивления, ВАХ которых не являются прямыми линиями (рис. 2.1, в), то есть они нелинейны, называют нелинейными, а электрические цепи с нелинейными сопротивлениями — нелинейными электрическими цепями.

Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности. Также как линейные в определенных диапазонах могут рассматриваться цепи, содержащие линейные усилители и некоторыми другими электронными устройствами, содержащими активные элементы, но имеющими в определенных диапазонах достаточно линейные характеристики.

Электрическая схема – это изображение электричес­кой цепи с помощью условных обозначений. Несмотря на всё многообразие цепей, каждая из них содержит эле­менты двух основных типов – это источники токов и потреби­тели.

Сопротивление – идеализированный пассивный элемент цепи, приближенно заменяющий резистор, в котором происходит необратимый процесс преобразования электрической энергии в неэлектрические виды энергии. R = U/i , Ом

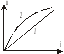Рис.1.1. Вольт-амперные характеристики линейного (1) и нелинейного (2) сопротивлений

Индуктивность – идеализированный пассивный элемент цепи, приближенно заменяющий катушку индуктивности, в которой происходит процесс накопления энергии магнитного поля.

L = /i, Гн;  = WФ, Вб. 0 (1.1)

Вебер-амперные характеристики линейной (1) и нелинейной (2) индуктивности представлены на Рис. 1 .2.

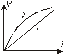Рис.1.2. Вебер-амперные характеристики линейной (1) и нелинейной (2) индуктивности

Ёмкость – идеализированный пассивный элемент цепи, приближенно заменяющий конденсатор, в котором происходит процесс накопления энергии электрического поля.

C = q/u , Ф.0 (1.2)

Кулон-вольтные характеристики линейной (1) и нелинейной (2) емкости представлены на Рис. 1 .3.

Кроме того, любая цепь характеризуется следующими основными топологическими понятиями.

Ветвь – это участок цепи, состав­ленный из после­довательно соединен­ных элементов цепи и расположен­ный между двумя узлами.

Узел – это точка цепи, где сходятся три или более ветвей.

Контур – это замкнутый путь, про­ходящий по не­скольким ветвям (Рис. 1 .4).

Рис.1.3. Кулон-вольтные характеристики линейной (1) и нелинейной (2) емкости

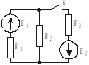
Рис.1.4. Электрический контур

Контур называется независимым, если в его составе при­сут­ствует хотя бы одна новая ветвь, ранее не входившая в другие контуры. В схеме на Рис. 1 .4 при замкнутом ключе имеем три контура, но лишь два из них неза­висимы.

Неразветвленные и разветвленные электрические цепи

Электрические цепи подразделяют на неразветвленные и разветвленные. Простейшая разветвленная цепь. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка, то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом

Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.

Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту от напряжения на этом компоненте называют вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.

В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.

Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.

Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть прменён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).

 

8.Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних (непотенциальных) сил висточниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил.

ЭДС так же, как и напряжение, измеряется в вольтах. Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил не во всем контуре, а только на данном участке. ЭДС гальванического элемента есть работа сторонних сил при перемещении единичного положительного заряда внутри элемента от одного полюса к другому. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы непотенциальны и их работа зависит от формы траектории. Так, например, работа сторонних сил при перемещении заряда между клеммами тока вне самого источника равна нулю.

ЭДС индукции :

Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением

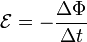
где — поток магнитного поля через замкнутую поверхность , ограниченную контуром. Знак «−» перед выражением показывает, что индукционный ток, созданный ЭДС индукции, препятствует изменению магнитного потока в контуре (см. правило Ленца).

 

9. Зако́н О́ма — физический закон, определяющий связь электродвижущей силы источника или электрического напряжения с силой тока и сопротивлением проводника. Экспериментально установлен в 1826 году, и назван в честь его первооткрывателя Георга Ома.

В своей оригинальной форме он был записан его автором в виде : ,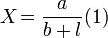

Здесь X — показания гальванометра, т.е в современных обозначениях сила тока I, a — величина, характеризующая свойства источника тока, постоянная в широких пределах и не зависящая от величины тока, то есть в современной терминологии электродвижущая сила (ЭДС) , l — величина, определяемая длиной соединяющих проводов, чему в современных представлениях соответствует сопротивление внешней цепи R и, наконец, b параметр, характеризующий свойства всей установки, в котором сейчас можно усмотреть учёт внутреннего сопротивления источника тока r^[1].

В таком случае в современных терминах и в соответствии с предложенной автором записи формулировка Ома (1) выражает

Закон Ома для полной цепи:

, (2)

где:

§ — ЭДС источника напряжения(В),

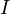§ — сила тока в цепи (А),

§ — сопротивление всех внешних элементов цепи (Ом),

§ — внутреннее сопротивление источника напряжения (Ом).

Часто ^[2]выражение:

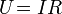(3)

(где 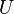есть напряжение или падение напряжения, или, что то же, разность потенциалов между началом и концом участка проводника) тоже называют «Законом Ома».

 

11. Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя

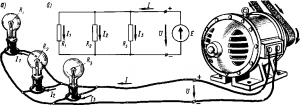Рис. 26. Схемы параллельного соединения приемников

лампы резисторами с сопротивлениями R1, R2, R3,

При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:

I₁=U/R₁; I₂=U/R₂; I₃=U/R₃.

Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I₁+I₂+I₃, или

I = U / R₁+ U / R₂+ U / R₃= U (1/R₁+ 1/R₂+ 1/R₃) = U / R_эк (23)

Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой

1/R_эк = 1/R₁+ 1/R₂+ 1/R₃ (24)

Вводя в формулу (24) вместо значений 1/R_эк, 1/R₁, 1/R₂ и 1/R₃ соответствующие проводимости G_эк, G₁, G₂ и G₃, получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов:

G_эк= G₁+ G₂+G₃ (25)

Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях

I₁: I₂: I₃= 1/R₁: 1/R₂: 1/R₃= G₁+ G₂+ G₃ (26)

В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи

R_эк=R₁R₂/(R₁+R₂)

при трех параллельно включенных резисторах

R_эк=R₁R₂R₃/(R₁R₂+R₂R₃+R₁R₃)

При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.

R_эк= R1 / n(27)

Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:

I1 = I / n (28)

При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-

Рис. 27. Схемы смешанного соединения приемников

ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
12. Правила Кирхгофа — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока.^{Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравненийотносительно токов или напряжений, и соответственно, найти значение токов на всех ветвях цепи и все межузловые напряжения. Сформулированы Густавом Кирхгофом в 1845 году. Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами Природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (3-е уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.}

Определения

Для формулировки правил Кирхгофа, вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют любой двухполюсник, входящий в цепь, например, на рис. отрезок, обозначенный U₁, I₁ есть ветвь. Узлом называют точку соединения двух и более ветвей (на рис. обозначены жирными точками). Контур — замкнутые циклы из ветвей. Термин замкнутый цикл означает, что начав с некоторого узла цепи и пройдя по нескольким ветвям и узлам однократно можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что каждая ветвь и узел может одновременно принадлежать нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило Кирхгофа

Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным: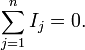

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

13. Электрический ток нагревает проводник. Это явление нам хорошо известно. Объясняется оно тем, что свободные электроны в металлах, перемещаясь под действием электрического поля, взаимодействуют с ионами или атомами вещества проводника и передают им свою энергию. В результате работы электрического тока увеличивается скорость колебаний ионов и атомов и внутренняя энергия проводника увеличивается. Опыты показывают, что в неподвижных металлических проводниках вся работа тока идет на увеличение их внутренней энергии. Нагретый проводник отдает полученную энергию окружающим телам, но уже путем теплопередачи. Значит, количество теплоты, выделяемое проводником, по которому течет ток, равно работе тока. Мы знаем, что работу тока рассчитывают по формуле:
А=U·I·t.
Обозначим количество теплоты буквой Q. Согласно сказанному выше Q = A, или Q = U·I·t. Пользуясь законом Ома, можно количество теплоты, выделяемое проводником с током, выразить через силу тока, сопротивление участка цепи и время. Зная, что U = IR, получим: Q = I·R·I·t, т. е. Q=I ·R·tКоличество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени. К этому же выводу, но на основании опытов впервые пришли независимо друг от друга английский ученый Джоуль и русский ученый Ленц. Поэтому сформулированный выше вывод называется законом Джоуля – Ленца

Читайте также:

Рекомендуемые страницы:

Поиск по сайту

Разветвленная цепь Википедия

Электрическая цепь
Условное обозначение электрической цепи
Изучается в	Теория электрических цепей[d]
Альтернативное имя	гальваническая цепь
Медиафайлы на Викискладе

Электри́ческая цепь (гальвани́ческая цепь) — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.

Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).

Классификация электрических цепей[ | ]

Неразветвленные и разветвленные электрические цепи[ | ]

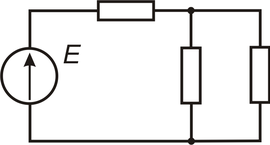Рисунок 1 — Разветвленная цепь

Электрические цепи подразделяют на неразветвленные и разветвленные. Во всех её элементах неразветвленной цепи течёт один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 1. В ней имеются три ветви и два узла. В каждой ветви течёт свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течёт одинаковый ток) и заключённый между двумя узлами. В свою очередь, узел есть точка цепи, в которой сходятся не менее трёх ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 1), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.

Линейные и нелинейные электрические цепи[ | ]

Линейной электрической цепью называют такую цепь, все компоненты которой линейные. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и катушки индуктивности. Если цепь содер

§23. Разветвлённые электрические цепи. Правила Кирхгофа

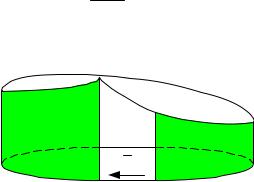
I =	ε
	R + r .	(22.11)

Как наглядно изобразить процесс, протекающий в замкнутой цепи постоянного тока?

A

B

Eст

Рис. 22.3

Точка А – соответствует положительной клемме источника, т. В – соответствует отрицательной клемме источника.

Процесс протекания тока можно представить так (рис. 22.3): положительные заряды – носители соскальзывают по наклонному желобу от точки А к точке В по внешнему участку цепи. Внутри источника от точки В к точке А их перемещают сторонние силы.

Расчет разветвлённых цепей, например нахождение токов в отдельных ветвях, значительно упрощается, при пользовании правилами Кирхгофа.

Узлом разветвлённой цепи называется точка, в которой сходятся три или более проводника. Ток текущий к узлу считается имеющим знак (+I), из узла – знак (–I).

Ветвью электрической цепи – называется участок цепи вдоль которого проходит один и тот же ток.

Первое правило Кирхгофа относится к узлам разветвлённых цепей.

n

∑ Ii = 0 (23.1)

i=1

Алгебраическая сумма токов сходящихся в узле равна 0.

Первое правило Кирхгофа вытекает из уравнения непрерывности, т.е. в конечном счёте, из закона сохранения заряда.

Первое правило Кирхгофа можно написать для каждого из N узлов цепи, но независимыми являются только (N – 1) уравнения, N-е будет следствием из них.

Второе правило Кирхгофа относится к любому, выделенному в разветвленной цепи замкнутому контуру.

Контур – любой замкнутый путь, который можно обойти, перемещаясь по любым ветвям цепи.

-+

+	—
R1		R2
	R3	I 2
1	—	3
		+

E

Рис. 23.1

Алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивления равна алгебраической сумме ЭДС, действующих в этом контуре.

∑ Ii Ri =∑ε k		(23.2)
i	k

Для доказательства рассмотрим контур:

Пусть обход контура совершается по часовой стрелке: тогда для каждого участка согласно, закон Ома:

I1R1 = (ϕ1 − ϕ2 ) + ε1

I2 R2 = (ϕ2 − ϕ2 ) + ε 2

I3 R3 = (ϕ3 − ϕ1 ) + ε 3

I1R1 + I2 R2 + I3R3 = ε1 + ε 2 + ε 3 ∑Ii Ri =∑ε k . i k

Таким образом, второе правило Кирхгофа является следствием закона Ома для неоднородного участка цепи.

Составление системы уравнений

Правила Кирхгофа в каждом конкретном случае позволяют написать полную систему уравнений, из которых могут быть найдены, например, все неизвестные токи.

3 х

1 x

Рис. 23.2

По 1 и 2 правилам Кирхгофа уравнений нужно составлять столько, сколько неизвестных величин, но надо следить, чтобы одни уравнения не являлись следствием других.

По 1 правилу Кирхгофа следует для цепи из N узлов записать (N – 1) независимых уравнений. По второму правилу Кирхгофа составлять уравнения только для независимых контуров.

Независимыми контурами являются те, которые нельзя составить наложением уже рассмотренных контуров. Число независимых уравнений по второму правилу Кирхгофа оказывается равным числу наименьших разрывов, которые нужно сделать, чтобы нарушить все контуры. Для такого контура (рис. 23.2) число независимых уравнений, составленных по 2-ому правилу Кирхгофа – 3.

При составлении уравнений по правилам Кирхгофа необходимо поступать так:

1.Произвольным образом выбрать направление токов на всех участках цепи; действительное направление токов определяется при решении задачи. Если при расчётах искомый ток получается отрицательным, то его истинное направление противоположно выбранному.

2.Выбрать направление обхода контура. Произведение Ii Ri считается положительным, если направление обхода и направление тока на данном участке совпадает, и считается отрица-

тельным (–Ii Ri), если направление обхода и направление тока на данном участке не совпадают. ЭДС берётся со знаком (+) если она действует в направлении обхода, или со знаком (–) если

против.

3. Составить столько уравнений по 1 и 2 правилам Кирхгофа, сколько неизвестных, и решить систему уравнений.

Модели: Цепи постоянного тока ОФ 1.0; Видеозадачи: 1) Загадка для лентяев; 2) Задуем лампочку – Видеозадачник, ч1, 3

§24. Закон Джоуля – Ленца

При протекании тока через проводник, обладающий сопротивлением, проводник нагревается (если он неподвижен и в нём нет химических превращений, то работа тока расходуется на нагревание проводника). Определим количество теплоты, выделяющегося в единицу времени на участке цепи. Рассмотрим однородный и неоднородный участки цепи, будем использовать закон Ома и закон сохранения энергии.

1)Однородный участок цепи

Рассчитаем работу, которую совершают силы поля над носителями тока на участке 1–2 за время dt. Сила тока в проводнике I, разность потенциалов между точками 1 и 2 – (ϕ1 – ϕ2). Тогда: dq = Idt – такой заряд протечёт через поперечное сечение участка 1-2.

dA = dq(ϕ1 − ϕ2 ) = I (ϕ1 − ϕ2 )dt

(24.1)

работа, совершаемая при перенесении заряда dq через поперечное сечение проводника на участке 1–2, силами поля.

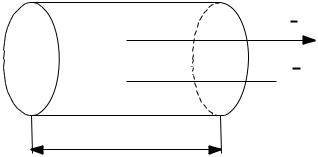
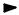E

dl

Рис. 24.1

Согласно закону сохранения энергии, энергия, эквивалентная этой работе, выделяется в виде тепла, если проводник неподвижен и в нём не происходят химические превращения, т.е. проводник нагревается. Носители тока (в металлах электроны) в результате работы сил поля приобретают дополнительную кинетическую энергию, а затем расходуют её на возбуждение коле-

баний решётки при столкновении с её узлами-атомами. Тогда:
dA = I(ϕ − ϕ	2	)dt =	I 2 Rdt .	(24.2)
1
Т.к. (ϕ1 − ϕ2 ) = IR , проинтегрировав, получаем:
A = I 2 Rt ,				(24.3)
но т.к.
Q = A = I 2 Rt	= IUt		= U 2t .	(24.4)
			R

Эта формула выражает закон Джоуля-Ленца для однородного участка цепи в интегральной форме записи. Если сила тока изменяется со временем, то количество теплоты, выделяющееся

за время t вычисляется по формуле:
					Q = ∫t	I 2 Rdt			(24.5)
					0
Получим дифференциальную форму записи закона Джоуля-Ленца.
j =	I	;	R = ρ	A	; dSdl = dV – величина элементарного объема.
				S
	S
					dQ = dA = I 2 Rdt = ( jdS )2 ρ		dA	dt = pj2dVdt	(24.6)
							dS

Формула (24.6) определяет тепло, выделяющееся во всём проводнике, можно перейти к выражению, характеризующему выделение тепла в различных местах проводника. Выделим в проводнике элементарный объём в виде цилиндра. Согласно закону Джоуля-Ленца за время dt в этом объеме выделяется тепло.

Разделив это выражение на dV и dt, найдём количество тепла, выделяющееся в единице объ-

ема в единицу времени, эту величину назвали удельной тепловой мощностью тока ω.

15

Удельная тепловая мощность тока – это количество теплоты выделяющееся в единицу времени в единице объема проводящей среды.

Тогда:
	dQ			= ρj2		dVdt	;	(24.7)
	dVdt					dVdt
			dQ		= ω ,			(24.8)
		dVdt
то
			ω = ρj2 .					(24.9)

Формула (24.9) – дифференциальная форма записи закона Джоуля-Ленца. Сформулируем его:

Удельная тепловая мощность тока пропорциональна квадрату плотности электрического тока и удельному сопротивлению среды в данной точке.

Уравнение ω = ρj2 применимо к любым проводникам вне зависимости от их формы, одно-

родности и от природы сил, возбуждающих электрический ток. Если на носители тока действуют только электрические силы, то, согласно закону Ома:

Gj = EG = σEG , и ω = ρj2 , то

ρ

ω = jE = σE 2 .

(24.10)

Это уравнение имеет менее общий характер, чем уравнение ω = ρj2 .

2)Неоднородный участок цепи

На неоднородном участке цепи на носители тока действуют не только электрические, но и сторонние силы, т.к. участок цепи содержит источник ЭДС. Тогда по закону сохранения энергии в неподвижном проводнике выделяемая теплота равна энергии, т.е. алгебраической сумме работ электрических и сторонних сил. Это же относится и к соответствующим мощностям: тепловая мощность должна быть равна алгебраической сумме мощностей электрических и сторонних сил:

P = UI = (ϕ1 − ϕ2 )I + ε12 I

(24.11)

P = UI – выделяющаяся на участке тепловая мощность. При наличии сторонних сил величина тепловой мощности определяется по той же формуле, что и для однородного участка цепи. Последнее слагаемое в правой части формулы: ε I – представляет собой мощность, развиваемую сторонними силами на данном участке цепи, но величина ε I – алгебраическая, в отличие от величины P = UI она изменяет знак при изменении направления тока I. Таким образом, данная формула означает, что тепловая мощность, выделяемая на участке цепи между точками 1 и 2, равна алгебраической сумме мощностей электрических и сторонних сил. Сумму этих мощно-

16

РАЗВЕТВЛЕННЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ С НЕСКОЛЬКИМИ ИСТОЧНИКАМИ

Для расчета и анализа цепей с несколькими источниками используются различные методы, некоторые из которых будут рассмотрены далее. В том случае, когда в разветвленной электрической цепи с несколькими источниками имеется группа активных или пассивных элементов, соединенных последовательно или параллельно, следует для упрощения расчета и анализа заменить их соответственно одним эквивалентным пассивным пли одним активным элементом. Иногда может показаться целесообразным использовать преобразование треугольника резистивных элементов в звезду.

Метод законов Кирхгофа.

Используя первый и второй законы Кирхгофа, можно для любой разветвленной электрической цепи составить необходимое число независимых уравнений и путем их совместного решения найти все подлежащие определению величины, например токи. Решая совместно уравнения, можно установить также зависимость между какими-либо величинами: между током и ЭДС, между двумя токами и т. д.

Перед составлением уравнений необходимо показать на схеме положительные направления известных и неизвестных величин. Сначала следует составить более простые уравнения по первому закону Кирхгофа, максимальное число которых должно быть на единицу меньше числа узловых точек. Недостающие уравнения следует составить по второму закону Кирхгофа.

Рис, 1.13. К расчету разветвленных электрических цепей с помощью законов Кирхгофа

 

В качестве примера составим схему уравнений для определения токов в электрической цепи, схема которой изображена на рис. 1.13. Будем считать, что ЭДС и напряжения с их направлениями, а также сопротивления известны. Поскольку данная цепь имеет пять ветвей с неизвестными токами, необходимо составить пять уравнений. Выбрав положительные направления токов I₁, I₂, I₃, I₄ и I₅, для узлов а и б, а также для контуров агда, абга и бвгб при обходе последних по часовой стрелке получим.

I₁ — I₃ + I₄ = 0; — I₂ -I₄ + I₅ = 0;

— Е₁ = — I₁ (r₁ + r₀₁)- I₃r₃ — U₁;

Е₁ — Е₂ = I₁ (r₁ + r₀₁) + I₂ (r₂ + r₀₂) — I₄r₄;

Е₂ = — I₂ (r₂ + r₀₂) — I₅r₅ + U₂.

Метод контурных токов.

Метод контурных токов дает возможность упростить расчет электрических цепей по сравнению с методом законов Кирхгофа за счет уменьшения числа уравнений, которые приходится решать совместно.

Дадим обоснование указанного метода.

Любая разветвленная электрическая цепь состоит из нескольких смежных контуров. Например, в электрической цепи ряс, 1.14 таких контуров три: абвга, бдвб и аедба. Каждый контур имеет несмежные ветви, принадлежащие лишь данному контуру, и смежные ветви, принадлежащие также соседним контурам. Так, контур абвга имеет несмежную ветвь вга и две смежные ветви аб и бв.

Рис. 1.14 К пояснению метода контурных токов

 

Допустим, что в каждом контуре рис. 1.14 имеется некоторый контурный ток, одинаковый для всех элементов контура. На рис. 1,14 контурные токи обозначены I_I, I_II и I_III. Положительные направления контурных токов могут быть выбраны произвольно. Наложим на контурные токи следующее условие: контурные токи должны быть равны по абсолютному значению токам несмежных ветвей соответствующих контуров.

Если удастся найти контурные токи, то через них легко определять и токи всех ветвей. В силу наложенного условия токи несмежных ветвей следует определять так: если выбрать положительное направление тока несмежной ветвисовпадающим с контурным током, то ток ветви должен быть равен контурному току; если же направить ток несмежной ветви против контурного тока, то он должен быть равен контурному току со знаком «-». Так, токи в несмежных ветвях цепи (рис. 1.14) будут равны

I₁ = I_I , I₃ = — I_II, I₆ = — I_III.

Чтобы выяснить, как определять токи смежных ветвей, выразим ток I₂ через токи I₁ и I₃ и заменим последние контурными токами: I₂ = I₁ + I₃ = I_I — I_II. Аналогично найдем

I₄ = I_I — I_III, I₅ = I_III — I_II

Как видно, со знаком « + » должен быть взят тот контурный ток, направление которого совпадает с направлением тока смежной ветви; контурный ток, направленный в противоположную сторону, должен быть взят со знаком «-».

Нетрудно доказать, что контурные токи могут быть определены путем совместного решения системы уравнений, составленных по второму закону Кирхгофа, в которые вместо падений напряжения от токов ветвей следует ввести падения напряжения от контурных токов с соответствующими знаками.

Уравнение по второму закону Кирхгофа при включении в него контурных токов в общем случае имеет вид

ΣE = ΣI_k r + ΣU_k . (1.36)

Для рассматриваемой цепи (рис. 1.14) уравнения будут:

Е₂ = — I₁r₀₂ + I_II(r₀₂ + r₃ + r₅) — I_IIIr₅ + U;

Е₁ — Е₂ — I₁(r₀₁ + r₀₂ + r₄) — I_II r₀₂ — I_IIIr₄;

0 = I_III (r₄ + r₅+ r₆)- I_Ir₄ — I_IIr₅.

При решении задач рассмотренным методом целесообразно выбирать положительные направления токов ветвей после определения контурных токов. В этом случае можно выбрать положительные направления токов ветвей так, чтобы все они совпадали с их действительными направлениями.

Метод узлового напряжения.

Метод узлового напряжения дает возможность весьма просто произвести анализ и расчет электрической цепи, содержащей несколько параллельно соединенных активных и пассивных ветвей, например цепи, схема которой изображена на рис 1.15,а.

Пренебрегая сопротивлением проводов, соединяющих ветви цепи, схему рис. 1.15, а можно заменить более удобной для рассмотрения (рис. 1.15,б).

В зависимости от значений и направлений ЭДС и напряжений, а также значений сопротивлений ветвей между узловыми точками а и b установится определенное узловое напряжение U_ab . Предположим, что оно направлено так, как показано на рис. 1.15, и известно. Зная напряжение U_ab , легко найти все токи.

Рис. 1.15. К пояснению метода узлового напряжения

 

Выберем положительные направления токов, например так, как показано на рисунке. Тогда по второму закону Кирхгофа для контура, проходящего по первой ветви,

Е₁ = I₁ (r₁ + r₀₁) + U_ab,

откуда

(1.37)

Поступая аналогичным способом, нетрудно получить формулы для токов I₂, I₃ и I₄:

I₂ = (Е₂ + U_ab)g₂, I₃ = (U₁ — U_ab )g₃, I₄ = (U₂ + U_ab)g₄. (1.38)

По закону Ома для пятой ветви

I₅ = U_ab /r₅ = U_ab g₅. (1.39)

Для вывода формулы, позволяющей определить напряжение U_ab , напишем уравнение по первому закону Кирхгофа для узла а:

I₁ — I₂ + I₃ — I₄ — I₅ = 0.

После замены токов их выражениями (1.37) — (1.39) и преобразований получим

,

Формула узлового напряжения в общем случае имеет вид

(1.40)

Перед определением напряжения по формуле (1.40) следует задаться его положительным направлением. Со знаком « + » в (1.40) должны входить ЭДС, направленные между точками а и b встречно напряжению U_ab и напряжения ветвей, направленные согласно с U_ab. Знаки в формуле (1.40) не зависят от направления токов ветвей.

При анализе и расчете электрических цепей методом узлового напряжения целесообразно выбирать положительные направления токов после определения узлового напряжения. В этом случае положительные направления токов нетрудно выбрать таким образом, чтобы все они совпадали с их действительными направлениями.

Пример 1.3. В электрической цепи рис. 1.15, б Е₁ = 40 В, Е₂ = 20 В, r₀₁ = r₀₂ = 1 Ом, r₁ = 9 Ом, r₂ = 39 Ом, r₃ = 10 Ом, r₄ = 30 Ом, r₅ = 15 Ом, U₁ = 45 В, U₂ = 30 В.

Пользуясь методом узлового напряжения, определить токи в ветвях.

Решение. По формулам (1.37) — (1.40) при указанных положительных направлениях напряжения U_ab и токов

I₁= (Е₁ — U_ab /(r₁ + r₀₁) ≈ 1,85 A,

I₂ = (E₂ + U_ab )/(r₂ + r₀₂ ) = 1,04 A;

I₃ = (U₁ — U_ab)/r₃ = 2,35 A;

I₄ = (U₂ + U_ab )/r₄ = 1,72 A;

I₅ = U_ab /r₅ = 1,44 A

Метод наложения.

Метод наложения основан на том, что в линейных электрических цепях ток любой ветви может быть определен как алгебраическая сумма токов от каждого источника в отдельности.

Расчет электрических цепей методом наложения производят в таком порядке. Из электрической цепи удаляют все источники ЭДС и напряжения, кроме одного. Сохранив в электрической цепи все резистивные элементы, в том числе и внутренние сопротивления источников, производят расчет электрической цепи. Внутренние сопротивления источников с указанными напряжениями полагают равными нулю. Подобным образом поступают столько раз, сколько имеется в цепи источников.

Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников. Для того чтобы результирующие токи совпадали с действительными направлениями, целесообразно выбирать положительные направления результирующих токов после определения токов от всех источников.

Метод наложения весьма удобен для анализа явлений, происходящих в электрических цепях при изменении их параметров.

Например, используя метод наложения, нетрудно определить характер изменения токов ветвей в цепи (см. рис. 1.15) при увеличении ЭДС Е₁ до Е’₁. Действительно, предположим, что при некоторых параметрах цепи до увеличения Е₁ установились токи, действительные направления которых совпадают с указанными на рисунке. Для решения задачи заменим мысленно увеличение ЭДС Е₁ введением в первую ветвь дополнительного источника с r_0доп = 0 и Е_доп = Е’₁— Е₁. После этого удалим из цепи все источники, кроме источника с ЭДС Е_доп, и определим действительные направления дополнительных токов от этого источника, которые очевидны.

Рис. 1.16. К пояснению метола эквивалентного генератора

 

Поскольку дополнительный ток первой ветви I_доп будет совпадать по направлению с током I₁, для определения результирующего тока первой ветви следует воспользоваться формулой

I’₁ = I₁ + I_1доп. На основании данной формулы можно сделать вывод о том, что при увеличении Е₁ ток I₁ будет возрастать. К такому же выводу можно прийти и в отношении токов других ветвей, кроме третьей.

Так как дополнительный ток третьей ветви I_3доп направлен против тока I₃, то для определения результирующего тока нужно использовать формулу I’₃ = I₃ — I_3доп. В отношении результирующего тока третьей ветви можно сделать такой вывод: при увеличении ЭДС Е₁ ток I₃ будет сначала уменьшаться, при некотором значении Е₁ окажется равным нулю, а при дальнейшем увеличении Е₁ изменит направление (I₃ < 0) и по абсолютному значению будет возрастать.

Метод эквивалентного генератора.

Метод эквивалентного генератора дает возможность упростить анализ и расчет электрических цепей в том случае, когда требуется определить ток, напряжение или мощность лишь одной ветви.

Предположим, что требуется найти ток I ветви amb некоторой электрической цепи (рис. 1.16, а), остальные элементы которой сосредоточены в пределах прямоугольника, представляющего собой активный двухполюсник А.

Согласно методу наложения ток I не изменится, если в данную ветвь ввести два источника, ЭДС которых Е₁ и Е_э равны и направлены в разные стороны (рис. 1.16,б). Ток I можно определить тогда как разность двух токов I = I_э — I₁, где I₁ — ток, вызванный всеми источниками двухполюсника А и ЭДС Е1 (рис, 1.16, в): I_э — ток, вызванный только ЭДС Е_э (рис. 1.16, г).

Если выбрать ЭДС Е₁ таким образом, чтобы получить I₁ = 0, то ток I будет равен

где r_0э — эквивалентное сопротивление двухполюсника А относительно выводов а и b.

Так как при I₁ = 0 (рис. 1.16,в) активный двухполюсник А будет работать относительно ветви amb в режиме холостого хода, то между выводами а и b установится напряжение холостого хода U = U_x и по второму закону Кирхгофа получим E₁ = I₁r + U_x = U_x . Но по условию Е_э = Е₁. поэтому и Е_э = U_x . Учитывая это, формулу для определения тока I можно записать в такой форме:

(1.41)

В соответствии с (1.41) электрическая цепь рис. 1.16,а может быть заменена эквивалентной цепью рис. 1.16, д, в которой Е_э = U_x и r_0э следует рассматривать как ЭДС и внутреннее сопротивление некоторого эквивалентного генератора. В результате возможности такой замены и возникло название изложенного метода

Значения Е_э = U_x и r_0э можно определить как расчетным, так и экспериментальным путем. Для расчетного определения U_x и r_0э необходимо знать параметры элементов активного двухполюсника А и схему их соединения. При определении сопротивления r0э необходимо удалить из схемы двухполюсника все источники, сохранив все резистивные элементы, в том числе и внутренние сопротивления источников ЭДС. Внутренние сопротивления источников с указанными напряжениями следует принять равными нулю.

Пример 1.4. В электрической цепи рис. 1.17, а U = 100 В, Е = 40 В, r₁ = r₄ = 30 Ом, r₂ = r₃ = 20 Ом, r = 15 Ом, r₀ = 1 Ом. Пользуясь методом эквивалентного генератора, определить ток I и напряжение U_ab .

Решение. При отключенном резистивном элементе r (рис. 1.17,б) по закону Ома и на основании второго закона Кирхгофа

, ,

Рис. 1.17. Схемы электрических цепей к примеру 1,4

После мысленного удаления из схемы рис. 1.17, б источников получим схему, изображенную на рис. 1,17,в. Глядя на эту схему, можно сделать заключение о том, что между точками а и b последовательно соединены три участка: участок с параллельно соединенными резисторами r₁ и r₃; участок, на котором параллельно соединены резисторы r₂ и r₄; участок, содержащий только резистор r₀. В соответствии с этим внутреннее сопротивление эквивалентного генератора (сопротивление цепи относительно точек а и b) будет

По формуле (1.41) и закону Ома

,

 

 

---

Дата добавления: 2018-03-20; просмотров: 428;

---

Правила Кирхгофа для разветвленных цепей

Чтобы расчеты сложных электрических цепей с неоднородными участками не вызывали трудности, существует упрощение с помощью применения правил Кирхгофа, которые рассматривают как обобщение закона Ома на случай разветвленных цепей.

В таких цепях выделяют узловые точки, называемые узлами, где сходятся не менее трех проводников, как изображено на рисунке 1.10.1. Токи, поступающие в узел, считают положительными, а вытекающие – отрицательными.

Рисунок 1.10.1. Узел электрической цепи. I1, I2>0; I3, I4<0.

Правила Кирхгофа. Примеры

Определение 1

В узлах цепи с постоянным током не происходит накопление зарядов. Получаем первое правило (закон) Кирхгофа:

Алгебраическая сумма сил токов для каждого узла разветвленной цепи равняется нулю:

I1+I2+I3+…+In=0.

Данное правило принято считать следствием закона сохранения электрического заряда.

Определение 2

Наличие разветвленной цепи позволяет выделить несколько замкнутых путей, которые состоят из однородных и неоднородных участков. Их принято называть контурами.

На участках с выделенным контуром могут протекать различные токи. Рисунок 1.10.2 наглядно показывает пример такой цепи, соответствующей 1 закону Кирхгофа. Она состоит из двух узлов a и d, в которых сходятся одинаковые токи. Только один из заданных узлов будет независимым.

Рисунок 1.10.2. Пример разветвленной электрической цепи. Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef).

В предложенной цепи выделяют три контура вида abcd,