Делитель напряжения на резисторах. Формула расчета, онлайн калькулятор

Делитель напряжения — это простая схема, которая позволяет получить из высокого напряжения пониженное напряжение.

Используя только два резистора и входное напряжение, мы можем создать выходное напряжение, составляющее определенную часть от входного. Делитель напряжения является одной из наиболее фундаментальных схем в электронике. В вопросе изучения работы делителя напряжения следует отметить два основных момента – это сама схема и формула расчета.

Схема делителя напряжения на резисторах

Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.

Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.

Расчет делителя напряжения на резисторах

Расчет делителя напряжения предполагает, что нам известно, по крайней мере, три величины из приведенной выше схемы: входное напряжение и сопротивление обоих резисторов. Зная эти величины, мы можем рассчитать выходное напряжение.

Формула делителя напряжения

Это не сложное упражнение, но очень важное для понимания того, как работает делитель напряжения. Расчет делителя основан на законе Ома.

Для того чтобы узнать какое напряжение будет на выходе делителя, выведем формулу исходя из закона Ома. Предположим, что мы знаем значения Uin, R1 и R2. Теперь на основании этих данных выведем формулу для Uout. Давайте начнем с обозначения токов I1 и I2, которые протекают через резисторы R1 и R2 соответственно:

Наша цель состоит в том, чтобы вычислить Uout, а это достаточно просто используя закон Ома:

Хорошо. Мы знаем значение R2, но пока неизвестно сила тока I2. Но мы знаем кое-что о ней. Мы можем предположить, что I1 равно I2. При этом наша схема будет выглядеть следующим образом:

Что мы знаем о Uin? Ну, Uin это напряжение на обоих резисторах R1 и R2. Эти резисторы соединены последовательно, при этом их сопротивления суммируются:

И, на какое-то время, мы можем упростить схему:

Закон Ома в его наиболее простом вид: Uin = I *R. Помня, что R состоит из R1+R2, формула может быть записана в следующем виде:

А так как I1 равно I2, то:

Это уравнение показывает, что выходное напряжение прямо пропорционально входному напряжению и отношению сопротивлений R1 и R2.

Делитель напряжения — калькулятор онлайн



 Применение делителя напряжения на резисторах

В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.

Потенциометры

Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.

Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.

Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.

Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.

Резистивные датчики

Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства. Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.

Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).

Пример работы делителя напряжения на фоторезисторе.

Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.

Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях — Help for engineer

Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях

Делитель напряжения используется в электрических цепях, если необходимо понизить напряжение и получить несколько его фиксированных значений. Состоит он из двух и более элементов (резисторов, реактивных сопротивлений). Элементарный делитель можно представить как два участка цепи, называемые плечами. Участок между положительным напряжением и нулевой точкой – верхнее плечо, между нулевой и минусом – нижнее плечо.

Делитель напряжения на резисторах может применятmся как для постоянного, так и для переменного напряжений. Применяется для низкого напряжения и не предназначен для питания мощных машин. Простейший делитель состоит из двух последовательно соединенных резисторов:

На резистивный делитель напряжения подается напряжение питающей сети U, на каждом из сопротивлений R1 и R2 происходит падение напряжения. Сумма U1 и U2 и будет равна значению U.

В соответствии с законом Ома (1):

Падение напряжения будет прямо пропорционально значению сопротивления и величине тока. Согласно первому закону Кирхгофа, величина тока, протекающего через сопротивления одинакова. С чего следует, что падение напряжения на каждом резисторе (2,3):

Тогда напряжение на всем участке цепи (4):

Отсюда определим, чему равно значение тока без включения нагрузки (5):

Если подставить данное выражение в (2 и 3), то получим формулы расчета падения напряжения для делителя напряжения на резисторах (6, 7):

Необходимо упомянуть, что значения сопротивлений делителя должны быть на порядок или два (все зависит от требуемой точности питания) меньше, чем сопротивление нагрузки. Если же это условие не выполняется, то при приведенном расчете подаваемое напряжение будет посчитано очень грубо.

Для повышения точности необходимо сопротивление нагрузки принять как параллельно подсоединенный резистор к делителю. А также использовать прецизионные (высокоточные) сопротивления.

Онлайн подбор сопротивлений для делителя

Пусть источник питания выдает 24 В постоянного напряжения, примем, что величина сопротивления нагрузки переменная, но минимальное значение равно 15 кОм. Необходимо рассчитать параметры резисторов для делителя, выходное напряжение которого равно 6 В.

Таким образом, напряжения: U=24 B, U₂=6 В; сопротивление резисторов не должно превышать 1,5 кОм (в десять раз меньше значения нагрузки). Принимаем R1=1000 Ом, тогда используя формулу (7) получим:

выразим отсюда R₂:

Зная величины сопротивления обоих резисторов, найдем падение напряжения на первом плече (6):

Ток, который протекает через делитель, находится по формуле (5):

Схема делителя напряжения на резисторах рассчитана выше и промоделирована:

Использование делителя напряжения очень неэкономичный, затратный способ понижения величины напряжения, так как неиспользуемая энергия рассеивается на сопротивлении (превращается в тепловую энергию). КПД очень низкий, а потери мощности на резисторах вычисляются формулами (8,9):

По заданным условиям, для реализации схемы делителя напряжения необходимы два резистора:

		1. R1=1 кОм, P1=0,324 Вт.
		2. R2=333,3 Ом, P2=0,108 Вт.

Полная мощность, которая потеряется:

---

Делитель напряжения на конденсаторах применяется в схемах высокого переменного напряжения, в данном случае имеет место реактивное сопротивление.

Сопротивление конденсатора рассчитывается по формуле (10):

		где С – ёмкость конденсатора, Ф;
		f – частота сети, Гц.

Исходя из формулы (10), видно, что сопротивление конденсатора зависит от двух параметров: С и f. Чем больше ёмкость конденсатора, тем сопротивление его ниже (обратная пропорциональность). Для ёмкостного делителя расчет имеет такой вид (11, 12):

Еще один делитель напряжения на реактивных элементах – индуктивный, который нашел применение в измерительной технике. Сопротивление индуктивного элемента при переменном напряжении прямо пропорционально величине индуктивности (13):

где L – индуктивность, Гн.

Падение напряжения на индуктивностях (14,15):

Недостаточно прав для комментирования

напряжения на резисторе и после

При разработке печатных плат для электронного оборудования специалистам часто приходится выполнять расчет делителя. С виду простая схема помогает уменьшить выходное напряжение, необходимое для питания отдельных элементов цепи. Такая компоновка является базовой для электроники. В основу изучения принципа действия входят два момента: схематическое исполнение и формула для вычисления параметров работы делителя.

Что такое делитель напряжения

Схематическое исполнение понижающего устройства представляет собой последовательную цепь, состоящую из двух резистивных элементов. Суммарные значения сопротивлений позволяют уменьшить входящее напряжение до необходимых параметров на выходе. Между собой они связаны передаточным коэффициентом, находящимся в интервале от 0 до 1, включая границы (0<=aplha<=1).

Общее представление делителя напряжения

Существует несколько вариантов схематического исполнения приборов, но все они обладают одним и тем же функционалом — понижать вольтаж для потребителей, однако ток на всех полюсах остается одинаковым. Два последовательных участка цепи называют плечами. Нижнее плечо находится между центральной точкой и нулевым потенциалом. Именно здесь необходимо снимать показатели работы схемы. Другое плечо является верхним.

 

Простая схема на резисторах

В зависимости от расположения резисторов, различают линейные и нелинейные схемы делителей. Первый вариант используют для создания разности потенциалов и вольтажа в нескольких точках рабочих узлов. Понижение входного напряжения определяется по линейному закону.

Дополнительная информация! Понижающие узлы применяют для постоянного и переменного тока. Структурное исполнение обоих отличается друг от друга, поскольку в некоторых случаях требует включение дополнительных фильтров для подавления помех и шумов.

В нелинейных схемах разница определяется по передаточному коэффициенту. Такие устройства активно применяют в потенциометрах. Здесь учитывают присутствие активного и реактивного сопротивления, включая нелинейные и токовые нагрузки.

Принцип работы делителя напряжения

В состав простейшей понижающей схемы всегда входит не меньше одного резистора. Если элементы обладают одинаковыми коэффициентами сопротивляемости электронов, то на выходе вольтаж понизится в два раза. Для каждого узла понижение рассчитывается по закону Ома.

Внимание! Сумма пониженных величин в каждой точке равна общему вольтажу источника питания.

Схема с несколькими резисторами

Резисторы используют в принципиальных схемах с источником питания постоянного тока. В цепях переменного напряжения присутствует еще и реактивное сопротивление, куда входят конденсаторы, индуктивные катушки и другие элементы с электромагнитными полями.

В цепях с синусоидальным током в качестве резистивного элемента выступает конденсатор или катушка. Их называют емкостными. Расчет ведется уже по другой формуле, так как емкость конденсаторов обратно пропорциональна их реактивному сопротивлению. Для вычисления резистивной составляющей необходимо учитывать постоянное число ПИ, частоту синусоидального тока (Гц) и емкость (Фарад). Таким образом получается, что с увеличением емкости падает сопротивление и наоборот.

Кроме конденсаторов, в качестве реактивных компонентов также могут выступать индуктивные катушки, которые могут присутствовать в платах переменного тока. Коэффициент реактивного сопротивления обмоток также прямо пропорционален их номинальным значениям. Для вычислений также необходимо постоянное число ПИ, частота переменного магнитного поля (Гц) и индуктивность (Генри).

Делитель на индукционных катушках

Внимание! В описании выше токовая нагрузка равна бесконечности, поэтому все значения верны только при полученных показателях делителя на сопротивления нагрузки. Они в несколько раз больше внутреннего.

Формула для расчета делителя напряжения

Начинающие радиолюбители часто задаются главным вопросом, как правильно рассчитать напряжение после резистора. Для этого необходимо знать, какой ток пойдет по цепи. В простейших схемах постоянного тока его вычисляют по линейному закону Ома. Формула расчета выглядит U=I*R, где:

• U — напряжение, В;
• I — ток, А;

В цепях с синусоидальным током, где присутствует реактивное сопротивление катушки или конденсатора, формула выглядит как R=1/(2*pi*f*L) и R=1/(2*pi*f*C) соответственно. В формуле использованы показатели:

График зависимости показателей от сопротивления

• R — реактивное сопротивление;
• R — сопротивление, Ом.
• pi — постоянное число Пи, равное 3,14;
• f — частота, Гц;
• L — индуктивность катушки, Генри;
• C — емкость конденсатора, Фарад.

Получив в расчетах внутреннюю резистивность элементов, далее можно воспользоваться линейной формулой для вычисления выходного значения.

На резисторе

В схеме делителя всегда участвует не меньше двух узлов нагрузки. Их коэффициенты могут быть равны другу, но и отличаться. Поэтому порой возникает необходимость получить номинал выходного вольтажа для каждого из них. Для этого используют всем известную формулу закона Ома: U=I*R.

После резистора

Для расчета показателя после резистора необходимо учитывать номиналы обоих элементов, так как они работают совместно друг с другом. Применив закон Ома, получается следующая формула: Uвых=Uпит*R1/(R1+R2), где:

• Uвых — вольтаж на выходе, В;
• Uпит — входной вольтаж, В;
• R1 — первый узел, Ом;
• R2 — второй узел, Ом.

Падение потенциалов за резистором рассчитывают для каждого узла в отдельности. То есть для второго элемента формула будет выглядеть так: Uвых=Uпит*R2/(R1+R2).

Делитель позволяет разработчикам получить несколько номинальных значений выходного напряжения от одного питающего источника. По этой причине схема получила широкое применение в электронике как в понижающих блоках питания, так и в качестве интегрированного узла электроцепи.

Как понизить напряжение переменного и постоянного тока?

За счет наличия большого количества международных стандартов и технических решений питание электронных устройств может осуществляться от различных номиналов. Но, далеко не все они присутствуют в свободном доступе, поэтому для получения нужной разности потенциалов придется использовать преобразователь. Такие устройства можно найти как в свободной продаже, так и собрать самостоятельно из радиодеталей.

В связи с наличием двух родов электрического тока: постоянного и переменного, вопрос,  как понизить напряжение, следует рассматривать в  ключе каждого из них отдельно.

Понижение напряжения постоянного тока

В практике питания бытовых приборов существует масса примеров работы электрических устройств от постоянного тока. Но номинал рабочего напряжения может существенно отличаться, к примеру, если из 36 В вам нужно получить 12 В, или в ситуациях, когда от USB разъема персонального компьютера нужно запитать прибор от 3 В вместо имеющихся 5 вольт.

Для снижения такого уровня от блока питания или другого источника почти вполовину можно использовать как простые методы – включение в цепь дополнительного сопротивления, так и более эффективные – заменить стабилизатор напряжения в ветке обратной связи.

Рис. 1. Замена резистора или стабилитрона

На рисунке выше приведен пример схемы блока питания, в котором вы можете понизить вольтаж путем изменения параметров резистора и стабилитрона. Этот узел на рисунке обведен красным кругом, но в других моделях место установки, как и способ подсоединения, может отличаться. На некоторых схемах, чтобы понизить напряжение вы сможете воспользоваться лишь одним стабилитроном.

Если у вас нет возможности подключаться к блоку питания – можно обойтись и менее изящными методами. К примеру, вы можете понизить напряжение за счет включения в цепь резистора или подобрать диоды, второй вариант является более практичным для цепей постоянного тока. Этот принцип основан на падении напряжения за счет внутреннего сопротивления элементов. В зависимости от соотношения проводимости рабочей нагрузки и полупроводникового элемента может понадобиться около 3 – 4 диодов.

Рис. 2. Понижение постоянного напряжения диодами

На рисунке выше показана принципиальная схема понижения напряжения при помощи диодов. Для этого они включаются в цепь последовательно по отношению к нагрузке. При этом выходное напряжение окажется ниже входного ровно на такую величину, которая будет падать на каждом диоде в цепи.  Это довольно простой и доступный способ, позволяющий понизить напряжение, но его основной недостаток – расход мощности для каждого диода, что приведет к дополнительным затратам электроэнергии.

Понижение напряжения переменного тока

Переменное напряжение в 220 Вольт повсеместно используется для бытовых нужд, за счет физических особенностей его куда проще понизить до какой-либо величины или осуществлять любые другие манипуляции. В большинстве случаев, электрические приборы и так рассчитаны на питание от электрической сети, но если они были приобретены за рубежом, то и уровень напряжения для них может существенно отличаться.

К примеру, привезенные из США устройства питаются от 110В переменного тока, и некоторые умельцы берутся перематывать понижающий трансформатор для получения нужного уровня. Но, следует отметить, что импульсный преобразователь, которым часто комплектуется различный электроинструмент и приборы не стоит перематывать, так как это приведет к его некорректной работе в дальнейшем. Куда целесообразнее установить автотрансформатор или другой на нужный вам номинал, чтобы понизить напряжение.

С помощью трансформатора

Изменение величины напряжения при помощи электрических машин используется в блоках питания и подзарядных устройствах. Но чтобы понизить  вольтаж источника в такой способ, можно использовать различные типы преобразовательных трансформаторов:

• С выводом от средней точки – могут выдавать разность потенциалов как 220В, так и в два раза меньшее – 127В или 110В. От него вы сможете взять установленный номинал на те же 110В со средней точки. Это заводские изделия, которые массово устанавливались в старых советских телевизорах и других приборах. Но у этой схемы преобразователя имеется существенный недостаток – если нарушить целостность обмотки ниже среднего вывода, то на выходе трансформатора получится номинал значительно большей величины.

Рис. 3. Понижение трансформатором с отводом от средней точки

• Автотрансформатором – это универсальная электрическая машина, которая способна не только понизить вольтаж, но и повысить его до нужного вам уровня. Для этого достаточно перевести ручку в нужное положение и проследить полученные показания на вольтметре.

Рис. 4. Использование автотрансформатора

• Понижающим трансформатором с преобразованием 220В на нужный вам номинал или с любого другого напряжения переменной частоты. Реализовать этот метод можно как уже готовыми моделями трансформаторов, так и самодельными. За счет наличия большого количества инструментов и приспособлений, сегодня каждый может собрать трансформатор с заданными параметрами в домашних условиях. Более детально об этом вы можете узнать из соответствующей статьи: https://www.asutpp.ru/transformator-svoimi-rukami.html

Выбирая конкретную модель электрической машины, чтобы понизить напряжение, обратите внимание на характеристики конкретной модели по отношению к тем устройствам, которые вы хотите запитать.

Наиболее актуальными параметрами у трансформаторов являются:

• Мощность – трансформатор должен не только соответствовать, подключаемой к нему нагрузке, но и превосходить ее, хотя бы на 10 – 20%. В противном случае максимальный ток приведет к перегреву обмоток трансформатора и дальнейшему выходу со строя.
• Номинал напряжения – выбирается и для первичной, и для вторичной цепи. Оба параметра одинаково важны, так как, выбрав модель с входным напряжением на 200 или 190В, на выходе вы при питании от 220В получится пропорционально большая величина.
• Защита от поражения электротоком – все обмотки и выводы от них должны обязательно иметь достаточную изоляцию и защиту от прикосновения.
• Класс пыле- влагозащищенности – определяет устойчивость оборудования к воздействию окружающих факторов. В современных приборах обозначается индексом IP.

Помимо этого любой преобразователь напряжения, даже импульсный трансформатор, следовало бы защитить от токов короткого замыкания и перегрузки в обмотках. Это существенно сократит затраты на ремонт при возникновении аварийных ситуаций.

С помощью резистора

Для понижения напряжения в цепь нагрузки последовательно включается  делитель напряжения в виде активного сопротивления.

Основной сложностью в регулировке напряжения на подключаемом приборе является зависимость от нескольких параметров:

• величины напряжения;
• сопротивления нагрузки;
• мощности источника.

Если  вы будете понижать от бытовой сети, то ее можно считать источником бесконечной мощности и принять эту составляющую за константу. Тогда расчет резистора будет выполняться таким методом:

R = U_c/I — R_н ,

где

• R – сопротивление резистора;
• R_Н – сопротивление прибора нагрузки;
• I – ток, который должен обеспечиваться в номинальном режиме прибора;
•  U_C – напряжение в сети.

После вычисления номинала резистора можете подобрать соответствующую модель из имеющегося ряда. Стоит отметить, что куда удобнее менять потенциал при помощи переменного резистора, включенного в цепь. Подключив его последовательно с нагрузкой, вы можете подбирать положение таким образом, чтобы понизить напряжение до необходимой величины. Однако эффективным способ назвать нельзя, так как помимо работы в приборе, электрическая энергия будет просто рассеиваться на резисторе, поэтому этот вариант является временным или одноразовым решением.

Бестрансформаторное электропитание.Конденсатор вместо резистора

В данной статье поговорим про бестрансформаторное электропитание.

В радиолюбительской практике, да и в промышленной аппаратуре источником электрического тока обычно являются гальванические элементы, аккумуляторы, или промышленная сеть 220 вольт. Если радиоприбор переносной (мобильный), то использование батарей питания себя оправдывает такой необходимостью. Но если радиоприбор используется стационарно, имеет большой ток потребления, эксплуатируется в условиях наличия бытовой электрической сети, то питание его от батарей практически и экономически не выгодно. Для питания различных устройств низковольтным напряжением от бытовой сети 220 вольт существуют различные виды и типы преобразователей напряжения бытовой сети 220 вольт в пониженное. Как правило, это схемы трансформаторного преобразования.

 

Схемы трансформаторного питания строятся по двум вариантам

 

1. «Трансформатор – выпрямитель — стабилизатор» — классическая схема питания, обладающая простотой построения, но большими габаритными размерами;

2. «Выпрямитель — импульсный генератор – трансформатор – выпрямитель – стабилизатор» — схема импульсного источника питания, обладающая малыми габаритными размерами, но имеющая более сложную схему построения.

Самое главное достоинство указанных схем питания – наличие гальванической развязки первичной и вторичной цепи питания. Это снижает опасность поражения человека электрическим током, и предотвращает выход аппаратуры из строя по причине возможного замыкания токоведущих частей устройства на «ноль». Но иногда, возникает потребность в простой, малогабаритной схеме питания, в которой наличие гальванической развязки не важно. И тогда мы можем собрать простую конденсаторную схему питания. Принцип её работы заключается в «поглощении лишнего напряжения» на конденсаторе. Для того, чтобы разобраться в том, как это поглощение происходит, рассмотрим работу простейшего делителя напряжения на резисторах.

Делитель напряжения состоит из двух резисторов R1 и R2. Резистор R1 – ограничительный, или по другому называется добавочный. Резистор R2 – нагрузочный (Rн), он же является внутренним сопротивлением нагрузки.

Предположим, что нам необходимо из напряжения 220 вольт получить напряжение 12 вольт. Указанные U2 = 12 вольт должны падать на сопротивлении нагрузки R2. Это означает, что остальное напряжение U1 = 220 – 12 = 208 вольт должно падать на сопротивлении R1.

Допустим, что в качестве сопротивления нагрузки мы используем обмотку электромагнитного реле, а активное сопротивление обмотки реле R2 = 80 Ом. Тогда по закону Ома, ток, протекающий через обмотку реле, будет равен: Iцепи = U2/R2 = 12/80 = 0,15 ампер. Указанный ток должен течь и через резистор R1. Зная, что на этом резисторе должно падать напряжение U1 = 208 вольт, по закону Ома определяем его сопротивление:

R1 = UR1 / Iцепи = 208/0,15 = 1 387 Ом.

Определим мощность резистора R1: Р = UR1 * Iцепи = 208 * 0,15 = 31,2 Вт.

Для того, чтобы этот резистор не грелся от рассеиваемой на нём мощности, реальное значение его мощности необходимо увеличить в раза два, это приблизительно составит 60 Вт. Размеры такого резистора довольно внушительны. И вот здесь нам пригодится конденсатор!

 

Мы знаем, что любой конденсатор в цепи переменного тока обладает таким параметром, как «реактивное сопротивление» — сопротивление радиоэлемента изменяющееся в зависимости от частоты переменного тока. Реактивное сопротивление конденсатора определяется по формуле:

где п – число ПИ = 3,14, f – частота (Гц), С – ёмкость конденсатора (фарад).

Заменив резистор R1 на бумажный конденсатор С, мы «забудем» что такое резистор внушительных размеров.

Реактивное сопротивление конденсатора С должно приблизительно равняться ранее рассчитанному значению R1 = Хс = 1 387 Ом.

Преобразовав формулу заменив местами величины С и Хс, мы определим значение ёмкости конденсатора:

С1 = 1 / (2*3,14*50*1387) = 2,3*10^-6 Ф = 2,3 мкФ

Это может быть несколько конденсаторов с требуемой общей ёмкостью, включенных параллельно, или последовательно.

Схема бестрансформаторного (конденсаторного) питания будет выглядеть следующим образом:

Но изображённая схема работать будет, но не так как мы планировали! Заменив массивный резистор R1 на один, или два малогабаритных конденсатора, мы выиграли в размерах, но не учли одно — конденсатор должен работать в цепи переменного тока, а обмотка реле – в цепи постоянного тока. На выходе нашего делителя переменное напряжение, и его необходимо преобразовать в постоянное. Это достигается вводом в схему диодного выпрямителя разделяющего входную и выходную цепь, а так же элементов сглаживающих пульсацию переменного напряжения в выходной цепи.

Окончательно, схема бестрансформаторного (конденсаторного) питания будет выглядеть следующим образом:

Конденсатор С2 — сглаживающий пульсации. Для исключения опасности поражения электрическим током от накопленного напряжения в конденсаторе С1, в схему введен резистор R1, который шунтирует конденсатор своим сопротивлением. При работе схемы он своим большим сопротивлением не мешает, а после отключения схемы от сети, в течение времени, определяемого секундами, через резистор R1 происходит разряд конденсатора. Время разряда определяется обыкновенной формулой:

Для того, чтобы следующий раз не делать все вышеперечисленные расчёты, выведем окончательную формулу расчёта ёмкости конденсатора схемы бестрансформаторного (конденсаторного) питания. При известных значениях входного и выходного напряжения, а также сопротивления R2 (оно же — сопротивление нагрузки Rн), значение сопротивления R1 находится в соответствии с пунктом 3 статьи «Делитель напряжения«:

Объединив две формулы, находим конечную формулу расчета ёмкости конденсатора схемы бестрансформаторного питания:

где Rн – сопротивление нагрузки, в нашем случае это – сопротивление обмотки реле Р1.

Учитывая, что при работе в переменном напряжении в конденсаторе происходят перезарядные процессы, а также сдвиг фазы тока по отношению к фазе напряжения, необходимо брать конденсатор на напряжение в 1,5…2 раза больше того напряжения, которое подаётся в цепь питания. При сети 220 вольт, конденсатор должен быть рассчитан на рабочее напряжение не менее 400 вольт.

По указанной выше формуле можно рассчитать значение ёмкости схемы бестрансформаторного питания для любого устройства, работающего в режиме постоянной нагрузки. Для работы в условиях переменной нагрузки, меняется также ток и напряжение выходной цепи. Для стабилизации выходного напряжения обычно применяют стабилитроны, или эквивалентные транзисторные схемы, ограничивающие выходное напряжение на необходимом уровне. Одна из таких схем показана на рисунке ниже.

Вся схема включена в сеть 220 вольт постоянно, а реле Р1 включается в цепь и выключается с помощью выключателя S1. В качестве выключателя может быть и полупроводниковый прибор, например транзистор. Транзисторный каскад VT1 включен параллельно нагрузке, он исключает увеличение напряжения во вторичной цепи. Когда нагрузка отключена, ток течёт через транзисторный каскад. Если бы этого каскада не было, то при отключении S1 и отсутствии другой нагрузки, на выводах конденсатора С2 напряжение могло бы достигнуть максимального сетевого – 315 вольт.

Стоит отметить, что при расчёте схем автоматики с реле, необходимо учитывать, что напряжение срабатывания реле, как правило, равно его номинальному (паспортному) значению, а напряжение удержания реле во включенном состоянии приблизительно в 1,5 раза меньше номинального. Поэтому, рассчитывая схему, изображённую выше, оптимально вести расчёт конденсатора для режима удержания, а напряжение стабилизации сделать равным номинальному (или чуть выше номинального). Это позволит работать всей схеме в режиме меньших токов, что повышает надёжность. Таким образом, для расчета емкости конденсатора С1 в схеме с коммутируемой нагрузкой, параметр Uвх мы берём равным не 12 вольт, а в полтора раза меньше – 8 вольт, а для расчёта ограничительного (стабилизирующего) транзисторного каскада – номинальное 12 вольт.

С1 = 1 / ( 2 * 3,14 * 50 * ( (220 * 80) / 8 – 80 ) ) = 1,5 мкФ
В качестве стабилизирующего элемента при малых токах можно использовать стабилитрон. При больших токах стабилитрон не годится – слишком малая у него рассеиваемая мощность. Поэтому в таком случае оптимально использовать транзисторную схему стабилизации напряжения. Расчёт стабилизирующего транзисторного каскада основан на использовании порога открытия биполярного транзистора, при достижении напряжения база-эмиттер 0,65 вольта (на кристалле кремния). Но учтите, что для разных транзисторов это напряжение колеблется в пределах 0,1 вольта, не только по типам, но и по экземплярам транзисторов. Поэтому напряжение стабилизации на практике может немного отличаться от рассчитанного значения.
Расчёт делителя смещения каскада стабилизации проводится всё по тем же формулам делителя напряжения, при известных Uвх.дел. = 12 вольт, Uвых.дел. = 0,65 вольт и токе транзисторного делителя, который должен быть приблизительно в двадцать раз меньше тока протекающего через ёмкость С1. Этот ток легко найти:Iдел. = Uвх.дел. / (20*Rн) = 12 / (20 * 80) = 0,0075 ампер,
где Rн – сопротивление нагрузки, в нашем случае это – сопротивление обмотки реле Р1, равное 80 Ом.

Номиналы резисторов R1 и R2 определяются по формулам, ранее опубликованным в статье «Делитель напряжения«:

,

где Rобщ – общее сопротивление резисторов делителя смещения транзистора VT1, которое находится по закону Ома:

Итак: Rобщ = 12 / 0,0075 = 1600 Ом ;

R3 = 0,65 * 1600 / 12 = 86,6 Ом , по номинальному ряду, ближайший номинал – 82 Ом;

R2 = 1600 – 86,6 = 1513,4 Ом , по номинальному ряду, ближайший номинал – 1,5 кОм.

Зная падение напряжения на резисторах и ток делителя, не забудьте рассчитать их габаритную мощность. С запасом, габаритную мощность R2 выбираем в 0,25 Вт, а R3 – в 0,125 Вт. Вообще, вместо резистора R2 лучше поставить стабилитрон, в данном случае это может быть Д814Г, КС211(с любым индексом), Д815Д, или КС212(с любым индексом). Я научил вас рассчитывать резистор намеренно.

Транзистор выбирается также с запасом падающей на его переходе мощности. Как выбирать транзистор в подобных стабилизирующих каскадах, хорошо описано в статье «Компенсационный стабилизатор напряжения«. Для лучшей стабилизации, возможно использование схемы «составного транзистора».

Думаю, что статья своей цели достигла, «разжёвано» всё до каждой мелочи.

Делитель напряжения — Википедия

Дели́тель напряже́ния — устройство, в котором входное Uin{\displaystyle U_{in}} и выходное Uout{\displaystyle U_{out}} напряжение связаны коэффициентом передачи 0⩽a⩽1{\displaystyle 0\leqslant a\leqslant 1}: Uout=a∗Uin{\displaystyle U_{out}=a*U_{in}}.^[1]

Делитель напряжения можно представить как два последовательных участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним (с него обычно снимается выходное напряжение делителя), а другое — верхним^[2]. Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента a{\displaystyle a} нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах.^[1] Сопротивление может быть как активным, так и реактивным, а также и вовсе нелинейным, как, например, в параметрическом стабилизаторе напряжения.

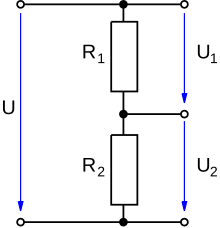Схема простейшего резистивного делителя напряжения

Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения U{\displaystyle U}. Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с первым правилом Кирхгофа. Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):

 U=IR{\displaystyle \ U=IR}.

Для каждого резистора имеем:
{U1=IR1U2=IR2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}\\U_{2}=IR_{2}.\end{array}}\right.}
Сложив выражения, получаем:

U1+U2=I(R1+R2).{\displaystyle U_{1}+U_{2}=I(R_{1}+R_{2}).}

Далее:

I=U1+U2R1+R2=UR1+R2.{\displaystyle I={\frac {U_{1}+U_{2}}{R_{1}+R_{2}}}={\frac {U}{R_{1}+R_{2}}}.}

Из этого следует:

{U1=IR1=UR1R1+R2U2=IR2=UR2R1+R2.{\displaystyle \left\{{\begin{array}{l l}U_{1}=IR_{1}=U{\frac {R_{1}}{R_{1}+R_{2}}}\\U_{2}=IR_{2}=U{\frac {R_{2}}{R_{1}+R_{2}}}.\end{array}}\right.}

Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно R2{\displaystyle R_{2}}, можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму:

1. Определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока, потребляемого нагрузкой (обычно принимают превышение от 10 раз по величине), но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения U{\displaystyle U}.

2. Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления R=R1+R2{\displaystyle R=R_{1}+R_{2}}.

3. Выбрать конкретные значения сопротивлений из стандартного ряда, отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетному сопротивлению R{\displaystyle R}.

При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления, допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность.

Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр, а в качестве нелинейного — параметрический стабилизатор напряжения.

Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ. В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.^[1]

Цепи обратной связи в усилителях[править | править код]

С помощью резистивного делителя напряжения в цепи обратной связи задаётся коэффициент усиления каскада на ОУ.

Простейшие электрические фильтры[править | править код]

RC, LC, RL-цепи, представляющие собой примеры простейших электрических фильтров, могут рассматриваться как частотно-зависимые делители напряжения, в которых в соответствующих плечах используются реактивные элементы.

Усилитель напряжения[править | править код]

Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если |R2|⩾|R1|{\displaystyle |R_{2}|\geqslant |R_{1}|}, а R1{\displaystyle R_{1}} — отрицательно, например как на участке вольт-амперной характеристики туннельного диода.

Параметрический стабилизатор напряжения[править | править код]

Делитель напряжения может использоваться для стабилизации входного напряжения — это возможно, если в качестве нижнего плеча делителя использовать стабилитрон.

Ограничения в применении резистивных делителей напряжения[править | править код]

Для обеспечения приемлемой точности работы делителя требуется проектировать его таким образом, чтобы величина тока, протекающего через цепи делителя, была не менее чем в 10 раз больше, нежели ток, протекающий через нагрузку. Увеличение этого соотношения до ×100, ×1000 и более при прочих равных условиях пропорционально повышает точность работы делителя. Таким же образом, вообще говоря, должны соотноситься и величины сопротивлений делителя и нагрузки. Нетрудно видеть, что идеальным (с точки зрения КПД) режимом работы делителя, является режим т.н. холостого хода, т.е. режим работы при отключенной нагрузке, когда её свойствами можно пренебречь. Увеличение тока нагрузки приводит к существенному падению КПД делителя, из-за того, что существенная часть мощности тратится на нагрев резисторов делителя. Вот почему резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы. Для решения этой задачи используют другие схемотехнические решения, в частности применяют стабилизаторы напряжения. Если же не требуется большой мощности, но требуется исключительно высокая точность поддержания величины выходного напряжения, то используют разнообразные источники опорного напряжения.

Нормативно-техническая документация[править | править код]

• ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока

1. ↑ ^{1 2 3} Словарь по кибернетике / Под редакцией академика В. С. Михалевича. — 2-е. — Киев: Главная редакция Украинской Советской Энциклопедии имени М. П. Бажана, 1989. — 751 с. — (С48). — 50 000 экз. — ISBN 5-88500-008-5.
2. ↑ В некоторых случаях возможно построение делителя напряжения по упрощённой схеме, когда в явном виде присутствует только верхнее плечо делителя, а в качестве нижнего плеча используется сопротивление самой нагрузки.