Расчет потерь напора по длине. Определение потерь давления
Посмотреть формулы для расчета потерь напора по длине.
Формулы для расчета потерь давления по длине
Данная автоматизированная система позволяет произвести расчет потерь напора по длине online. Расчет производится для трубопровода, круглого сечения, одинакового по всей длине диаметра, с постоянным расходом по всей длине (утечки или подпитки отсутствуют). Расчет производится для указанных жидкостей при температуре 20 град. С. Если вы хотите рассчитать потери напора при другой температуре, или для жидкости отсутствующей в списке, перейдите по указанной выше ссылке — Я задам кинематическую вязкость и эквивалентную шероховатость самостоятельно.
Для получения результата необходимо правильно заполнить форму и нажать кнопку рассчитать. В ходе расчета значения всех величин переводятся в систему СИ. При необходимости полученную величину потерь напора можно перевести в потери давления.
Порядок расчета потерь напора
- Вычисляются значения:
- средней скорости потока
- числа Рейнольдса — Re где V — средняя скорость течения жидкости, м/с, d — диаметр живого сечения, м, ν — кинематический коэффициент вязкости, кв.м/с, Rг — гидравлический радиус, для круглой трубы Rг=d/4, d — внутренний диаметр трубы, м
Определяется режим течения жидкости и выбирается формула для определения коэффициента гидравлического трения.
- Для ламинарного течения Re<2000 используются формула Пуазеля.
- Для переходного режима 2000<Re<4000 — зависимость:
- Для турбулентного течения Re>4000 универсальная формула Альтшуля. где к=Δ/d, Δ — абсолютная эквивалентная шероховатость.
Потери напора по длине трубопровода вычисляются по формуле Дарси — Вейсбаха.
Потери напора и давления связаны зависимостью.
Δp=Δhρg где ρ — плотность, g — ускорение свободного падения.
Потери давления по длине можно вычислить используя формулу Дарси — Вейсбаха.
После получения результатов рекомендуется провести проверочные расчеты. Администрация сайта за результаты онлайн расчетов ответственности не несет.
Как правильно заполнить форму
Правильность заполнения формы определяет верность конечного результата. Заполните все поля, учитывая указанные единицы измерения. Для ввода чисел с десятичной частью используйте точки.
www.hydro-pnevmo.ru
Расчет потерь напора в трубопроводах
16 ноября 2015 г.
В процессе течения нефтепродуктов имеют место потери напора на трение hτ и местные сопротивления hMC.
Потери напора на трение
Потери напора на трение при течении ньютоновских жидкостей в круглых трубах определяются по формуле Дарси—Вейсбаха
где λ — коэффициент гидравлического сопротивления; L, D — соответственно длина и внутренний диаметр трубопровода; W — средняя скорость перекачки; g — ускорение силы тяжести.
Величина коэффициента гидравлического сопротивления λ в общем случае зависит от числа Рейнольдса Re = W • D/v и относительной шероховатости труб ε = kэ/D (здесь v — кинематическая вязкость нефтепродукта при температуре перекачки; кэ — эквивалентная шероховатость стенки трубы).
При ламинарном режиме перекачки (Re = ReKp) расчет λ выполняется по формуле Стокса
λ = 64/Re
В переходной зоне (ReKp < Re < Rerp) расчет λ наиболее точно может быть выполнен по формуле Гипротрубопровода
λ=(0,16·Re-13)·10-4
Эквивалентная шероховатость kэ стальных труб
Вид труб | Состояние труб | К-,, мм | |
Диапазон изменения | Среднее значение | ||
Бесшовные | Новые и чистые | 0,01-0,02 | 0,014 |
Сварные | Новые и чистые | 0,03-0,12 | 0,05 |
С незначительной коррозией после очистки | 0,1-0,2 | 0,15 | |
После нескольких лет эксплуатации | 0,15-0,3 | ||
Умеренно заржавленные | 0,3-0,7 | 6,5 | |
Старые заржавленные | 0,8-1,5 | 1 | |
Сильно заржавленные или с большими отложениями | 2-4 | 3 | |
В зоне гидравлически гладких труб турбулентного режима (ReKp < Re < Rel) расчет λ выполняется по формуле Блазиуса
Для расчета λ в зоне смешанного трения турбулентного режима (ReI < Re = ReII) наиболее часто используется формула Альтшуля
В зоне квадратичного трения турбулентного режима (Re > ReII) расчет λ обычно ведут по формуле Шифринсона
Нетрудно видеть, что формулы Стокса, Блазиуса и Шифринсона могут быть представлены зависимостью одного вида
где А, т — коэффициенты, величина которых для каждой зоны трения неизменна.
Однако формула Альтшуля к этому виду не приводится. Это исключает возможность решения гидравлических задач в общем виде.
Ту же задачу можно было решить следующим образом. При Re = ReI еще справедлива формула Блазиуса, а при Re = RеI уже можно пользоваться формулой Шифринсона. Учитывая, что переходные числа Рейнольдса Альтшулем рекомендовано находить по формулам:
ReI=10/ε; ReII=500/ε.
для зоны смешанного трения получаем:
Поделив почленно получим:
откуда
Различие в выражениях для расчета коэффициента А объясняется тем, что в первом случае не было сделано необходимое алгебраическое преобразование
Среднеквадратичная погрешность аппроксимации В.ДБелоусова по сравнению с формулой Альтшуля составляет около 5%. Связано это, в частности, с тем, что ее автор не стремился сделать погрешность вычислений минимальной, а исходил из условия равенства коэффициентов X на границах зоны смешанного трения и соседних зон.
Автору совместно с аспиранткой Н.В. Морозовой удалось свести уравнение Альтшуля к виду со среднеквадратичной погрешностью 2,6%. Это было сделано следующим образом.
Представим формулу Альтшуля в виде
Недостатком данной записи является то, что расчетный коэффициент 0,11(68 + ε · Re) °-25 является функцией числа Рейнольдса. Вместе с тем из формул следует, что в зоне смешанного трения справедливо неравенство
10 < ε · Re < 500.
Задаваясь значениями г • Re в этом диапазоне, сначала рассчитали величины функции 0,11(68 + ε · Re)0’26, а затем, используя метод наименьших квадратов, заново описали полученные точки выражением 0,206( ε · Re)0’15.
Подставив его получили искомую зависимость
Из нее видно, что в зоне смешанного трения турбулентного режима величины коэффициентов А и т равны 0,206 • е0,15 и 0,1 соответственно. Среднеквадратичная погрешность расчетов по формуле относительно формулы Альтшуля — менее 3%, что меньше, чем по другим известным аппроксимациям.
Следует подчеркнуть, что учет наличия переходной зоны приводит к изменению критического числа Рейнольдса. Кроме того, А.Д. Альтшуль, строго говоря, для переходных чисел Рейнольдса рекомендует диапазоны
Чтобы уточнить величины Reкр, ReI ReII и найти величину Re.x,, воспользуемся следующим способом. При Re = ReKp еще справедлива формула Стокса» но в то же время уже справедлива формула Гипротрубопровода. То есть можно составить уравнение
Освобождаясь от знаменателя, получаем квадратное уравнение 0,16-10-4 · Reкр-13 · 10-4 · Reкp-64 = 0, единственным положительным корнем которого является Re
Рассуждая аналогично, можно найти все остальные характерные числа Рейнольдса. Приравняв формулы Гипротрубопровода и Блазиуса, получаем Reкp = 2800. Из равенства правых частей формулы Блазиуса и формулы находим, что ReI = 17,5/ε. Наконец, приравняв правые части формулы и формулы Шифринсона, несложно найти, что ReII = 531/ε.
В тех случаях, когда необходимо, чтобы зависимость потерь напора на трение от расхода Q была выражена в явном виде, удобно использовать обобщенную формулу Лейбензона
где β — расчетный коэффициент, равный
Формула получается подстановкой выражения в формулу Дарси—Вейсбаха .
Учитывая, что формулу Гипротрубопровода можно привести к виду
Рекомендуемые величины коэффициентов А, β и m
Режим течения | Зона трения | Область использования | A | β | m |
Лами нарный |
| Re< 2040 | 64 | 4,15 | 1 |
Переходная зона | 2040 <Re< 2800 | 1,17610-5 | 1,25-10-6 | -1,035 | |
Турбу- лентный | Г идравлически гладкие трубы | 2800 <Re< Re | 0,3164 | 0,0246 | 0,25 |
Смешанного трения | ReI <Re< ReII | 0,206 •£ 015 | 0,0166-e0,15 | 0,1 | |
Квадра тичного трения | Re > Ren | 0J1 e0—25 | 0,0091 -e025 | 0 |
Для вычисления потерь напора на трение при течении нефтепродуктов, проявляющих вязкопластичные свойства, можно воспользоваться уравнением Букингема (в виде аппроксимации, полученной проф. В.Е. Губиным)
где ΔР — перепад давления при течении вязкопластичной жидкости со средней скоростью W в трубопроводе диаметром D и длиной L; η — пластическая вязкость; F(И) — расчетная функция
где И — число Ильюшина
Потери напора на местные сопротивления
Данный вид потерь напора определяется по формуле Вейсбаха
где ξ — коэффициент местного сопротивления.
Величина коэффициента ξ, зависит от вида местного сопротивления и режима течения.
При ламинарном режиме течения величину коэффициента местного сопротивления следует вычислять по формуле
где ξг — коэффициент местного сопротивления при турбулентном режиме; А2 — постоянный коэффициент.
Коэффициенты местных сопротивлений при турбулентном режиме течения
Вид местного сопротивления | А2 | ξг |
Чялвижка открытая: | ||
— на 100% | 75 | 0,15 |
— на 75% | 350 | 0,20 |
— на 50% | 1300 | 2,00 |
— на 25% | 3000 | 20,0 |
Вентиль стандартный: | ||
— Dv = 80-100 мм | 3000 | 4,0 |
— Dy = 150-200 мм | — | 4,7 |
— Dy. = 250-300 мм | 5000 | 5,3 |
Обратный клапан: | ||
— Dy80-100 мм | — | 8,0 |
— Dy150-200 мм | — | 4,0 |
— Dy = 250-300 мм | — | 2,0 |
Компенсатор сальниковый | — | 0,2 |
Компенсатор П-образный: | ||
— Dy= 50-100 мм | 5000 | 2,2 |
— Dy = 200-300 мм | — | 2,4 |
— Dy = 400-500 мм | — | 2,8 |
Фильто для нефтепродуктов: | ||
— светлых | — | 1,70 |
— темных | — | 2,20 |
ros-pipe.ru
| № п/п | Наименование параметра | Обозначение | Размерность | Значение |
| Исходные данные | ||||
| 1 | Теплоноситель | среда | — | вода |
| 2 | Температура теплоносителя (подача) | t1 | oC | |
| 3 | Температура теплоносителя (обратка) | t2 | oC | |
| 4 | Тепловая мощность | Q | кВт | |
| 5 | Длина участка (подача + обратка) | L | м | |
| 6 | Сумма местных сопротивлений | ξ | — | |
| 7 | Диаметр трубопровода | Dn | мм | 1012152025324050658090100125150 |
| 8 | Тип трубопровода | Бесшовные стальные трубыСтальные сварные трубыЧугунные трубыАсбестоцементныеЖелезобетонныеПластиковыеСтеклянныеАлюминиевые | ||
| Результаты вычислений | ||||
| 1 | Средняя температура теплоносителя | tср | oC | |
| 2 | Плотность теплоносителя при средней температуре | ρ | кг/м3 | |
| 3 | Кинематический коэффициент вязкости | ν | м2/с х 10-6 | |
| 4 | Расход теплоносителя | G | кг/ч | |
| 5 | Скорость теплоносителя в трубопроводе | v | м/с | |
| 6 | Критерий Рейнольдса | Re | ||
| 7 | Гидродинамическое давление | ρϑ2/2 | Па | |
| 8 | Коэффициент гидравлического трения | λ | ||
| 9 | Линейные потери давления на трение | RL | Па | |
| 10 | Потери давления на местные сопротивления | Z | Па | |
| 11 | Суммарные потери давления | ΔP | Па | |
| 12 | Объем системы | V | л | |
helpeng.ru
Задача №1. Расчет коротких трубопроводов.
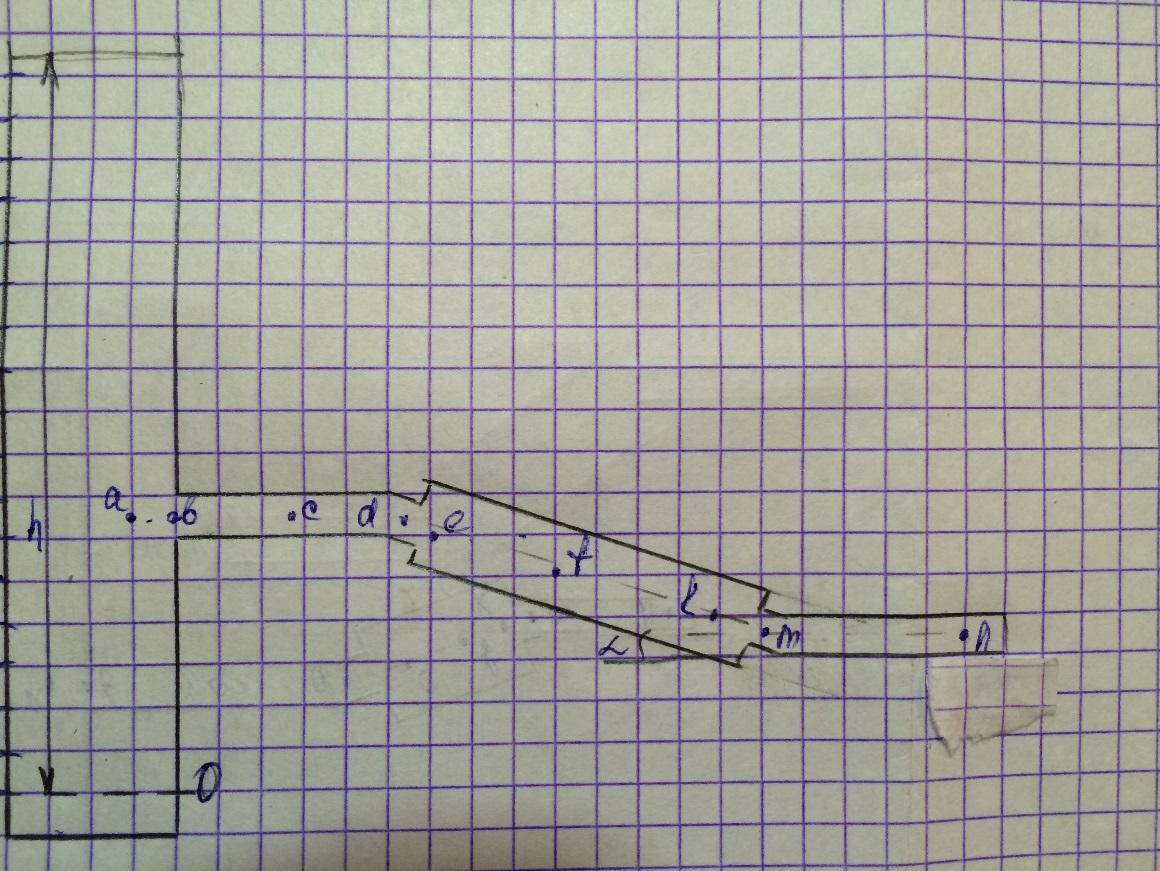 Рис.1.
Схема расположения трубопроводов.
Рис.1.
Схема расположения трубопроводов.
При расчете коротких трубопроводов применяется уравнение Бернулли для двух выбранных сечений и уравнение неразрывности.
Уравнение Бернулли составляется относительно плоскости сравнения, которой может быть любая горизонтальная плоскость. Плоскость сравнения проведена по центру трубы в начале трубопровода.
Расчет необходимо начать с определения формы записи уравнения Бернулли. Для расчета систем водоснабжения и водоотведения обычно применяется уравнение Бернулли в форме напоров:
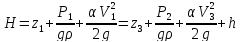 ,
,
где
высота z
называется геометрической высотой, или
высотой положения центра тяжести сечения
струйки; 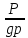 – высота, определяемая величиной
гидродинамического давления, или
пьезометрическая высота;
– высота, определяемая величиной
гидродинамического давления, или
пьезометрическая высота;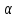 — коэффициент
— коэффициент
Кориолиса;  – скоростная высота, или скоростной
напор;
– скоростная высота, или скоростной
напор;  — потери напора.
— потери напора.
Если трубопровод имеет участки с разными диаметрами, то потери напора h при движении жидкости от сечения 1-1 к сечению 3-3 складываются из потерь во всех участках трубопровода. В каждом участке потери разделяются на потери по длине и местные.
1. Скорости потоков в трубах
Скорость потоков в трубах:
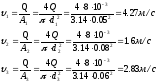
2. Расчёт потерь напора в трубопроводах
Потери
на выходе потока из бака определяется
по формуле
Вейсбаха: 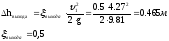
ζвыхода – коэффициент местного сопротивления
Потери напора по длине рассчитываются по формуле Дарси-Вейсбаха (труба 1):
Для определения потерь напора по длине трубы рассчитаем число Рейнольдса, по рассчитанному числу узнаем режим движения жидкости для всех участков с различными средними скоростями движения жидкости. Коэффициент гидравлического трения λ определяется по формулам, которые выбираются в зависимости от режима движения и области сопротивления.
Найдём число Рейнольдса

Число Рейнольдса определяет характер потока: ламинарный, промежуточный или турбулентный.
ламинарный , если Re <2300
промежуточный, если 2300 < Re <4000
турбулентный, если 4000 < Re
Зависимость коэффициента гидравлического сопротивления от числа Рейнольдса и эквивалентной шероховатости труб
Режим (зона) | Границы | Коэффициент гидравлического трения | |
Ламинарный | Re<2320 | | |
Турбулентный: | |||
1. | Зона перехода турбулентного движения в ламинарное | 2000<Re<3000 | |
2. | Зона гидравлически гладких труб | 2320<Re<10d/kэ | |
3. | Зона смешанного трения или гидравлически шероховатых труб | 10d/kэ<Re<500d/kэ | |
4. | Зона квадратичного сопротивления (вполне шероховатого трения) | Re>500d/kэ | |
Режим
движения жидкости турбулентный, так
как Re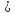 4000. Трубопровод гидравлически шероховатый,
1—
коэффициент гидравлического трения
рассчитывается по формуле Шифринсона:
4000. Трубопровод гидравлически шероховатый,
1—
коэффициент гидравлического трения
рассчитывается по формуле Шифринсона:
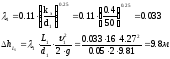
Потери напора на повороте:
ζпов.1 = ζ90° (1-cos20°)=0.06 м
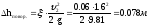
Потери напора при внезапном расширении рассчитывается по формуле Борда:
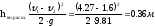
Потеря напора по длине (труба 2):
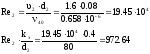
Режим
движения жидкости турбулентный, так
как Re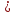 2320.
2320.
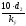
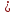 Re
Re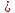
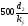 ;
4000 < 194529 < 200000
;
4000 < 194529 < 200000
Трубопровод гидравлически шероховатый.
Рассчитаем потери напора при внезапном сжатии:
n — коэффициент сжатия потока
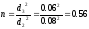
Коэффициент сужения струи находим по формуле Альтшуля:
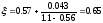
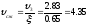
Потерю напора при внезапном сжатии находим по формуле Борда:
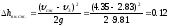
Потери напора на повороте:
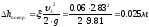
Потери напора по длине (труба 3):
Найдем число Рейнольдса:

Режим
движения жидкости турбулентный, так
как Re 2320. Трубопровод гидравлически шероховатый,
3—
коэффициент гидравлического трения
рассчитывается по формуле Альтшуля.
Потери
напора по длине рассчитываются по
формуле Дарси-Вейсбаха.
2320. Трубопровод гидравлически шероховатый,
3—
коэффициент гидравлического трения
рассчитывается по формуле Альтшуля.
Потери
напора по длине рассчитываются по
формуле Дарси-Вейсбаха.
Рассчитаем суммарные потери напора:
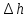 =
=  = 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м
= 0,465+9,8+0,36+0,0078+0,0047+0,025+0,12+2,53=13,31м
studfile.net

 (формула
Стокса)
(формула
Стокса)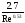 (формула
Френкеля)
(формула
Френкеля) (формула
Блазиуса)
(формула
Блазиуса) (формула
Конакова при Re<3*106)
(формула
Конакова при Re<3*106)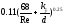 (формула
Альтшуля)
(формула
Альтшуля)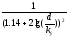 (формула
Никурадзе)
(формула
Никурадзе)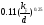 (формула
Шифринсона)
(формула
Шифринсона)