Расчет нагрузки | Режимщик
Расчет однофазных нагрузок
Нагрузка от однофазных ЭП в трехфазной сети определяется так же, как и от трехфазных, при условии, что она равномерно распределена по фазам или ее неравномерность H ≤ 15 % от суммарной номинальной мощности всех приемников, присоединенных к узлу питания.
Однофазные нагрузки включаются на фазное или линейное напряжение. В зависимости от числа однофазных ЭП и схемы их включения в трехфазную сеть при H > 15 % мощность однофазных ЭП приводится к условной трехфазной номинальной мощности Рн.у следующими способами:
— Один ЭП включен на фазное напряжение Рн.у = 3·Рном.ф.
— Один ЭП включен на линейное напряжение Рн.у = 3 ·Рном.л.
При числе однофазных ЭП менее 4 и включенных на фазное напряжение
Рн.у = 3·Рном.ф,
где Рном.ф – номинальная мощность ЭП наиболее загруженной фазы, кВт.
При числе однофазных ЭП менее 4 и при включении их на линейное напряжение в разные плечи трехфазной системы
Рн.у = 3·Рном.ф ,
где Рном.ф определяется как полусумма нагрузок двух плеч, прилегающих к данной фазе;
При смешанной схеме включения однофазных ЭП (одного на фазное, а второго на линейное напряжение) определяются условные мощности, приведенные к каждой фазе, причем за основу расчета принимается большая мощность Рн.у = 3·Рном.ф.
Расчетная активная нагрузка при n ≥ 4 однофазных ЭП с одинаковыми КИ и cosф, независимо от схемы включения определяется по формуле
Ррасч = 3·Ки·Км·Рном.ф,
где Рном.ф – номинальная активная мощность наиболее загруженной фазы.
В этом случае эффективное число ЭП
nэ = 2∑Рн.о/(3Рном),
где ∑Рно – сумма номинальных мощностей однофазных приемников данного расчетного узла;
Рном – номинальная мощность наибольшего однофазного ЭП.
Определение условной трехфазной мощности, создаваемой в трехфазной сети однофазными ЭП
Сегодня очень важная тема для проектировщиков, в которой я представлю свою обновленную программу. При расчете электрических нагрузок приходится приводить мощность однофазных ЭП к условной трехфазной мощности согласно РТМ 36.18.32.4-92.
Если вы не знакомы с моей программой для расчета электрических нагрузок, то сперва советую ознакомиться с тем, что было ранее.
В предыдущей версии программы условную трехфазную мощность необходимо было считать на калькуляторе и держать в голове все условия приведения мощности однофазных ЭП к условной трехфазной мощности.
Как я уже упоминал, сейчас я занимаюсь переработкой своих программ и решил расширить функционал программы по расчету электрических нагрузок.
По сравнению со старой программой, здесь я изменил цветовое оформление, добавил расчет тока для двигателей и разработанную мной форму расчета условной трехфазной мощности, создаваемой в трехфазной сети однофазными электроприемниками.
Последовательность расчета лучше всего рассмотреть на примере.
Допустим, нам требуется посчитать расчетную мощность, потребляемый ток, коэффициент мощности электрического щита, к которому подключены следующие трехфазные и однофазные ЭП:
Наименование ЭП | 3Р/1Р | Количество, шт. | Р, кВт | Ки | cosϕ |
| Станок 1 | 3Р | 3 | 3 | 0,2 | 0,7 |
| Станок 2 | 3Р | 5 | 1,5 | 0,2 | 0,7 |
| Насос | 3Р | 2 | 7,5 | 0,6 | 0,8 |
| Транспортер | 3Р | 1 | 5 | 0,4 | 0,75 |
| Сварочная машина | 3Р | 15 | 0,3 | 0,7 | |
| Индукционная печь | 3Р | 1 | 10 | 0,7 | 0,95 |
| Зарядное устройство | 3Р | 2 | 3 | 0,7 | 0,65 |
| Компьютер | 1Р | 5 | 0,3 | 0,5 | 0,7 |
| Рукосушитель | 1Р | 6 | 1,4 | 0,4 | 0,9 |
| Освещение | 1Р | 1 | 0,7 | 1 | 0,92 |
| Чайник | 1Р | 1 | 2,0 | 0,2 | 1 |
| Микроволновая печь | 1Р | 1 | 1,0 | 0,2 | 0,8 |
| Кондиционер | 1Р | 2 | 1,5 | 0,8 | 0,8 |
| Холодильник | 1Р | 2 | 0,2 | 0,7 | 0,8 |
| Вентилятор | 1Р | 3 | 0,5 | 0,6 | 0,8 |
| Электрическая плита | 1Р | 1 | 7,5 | 0,4 | 1,0 |
| Телевизор | 1Р | 3 | 0,1 | 0,7 | 0,8 |
Как определить условную трехфазную мощность, создаваемую в трехфазной сети однофазными ЭП?
В РТМ 36.18.32.4-92 по этому поводу сказано лишь следующее:
3.2.1.7. При наличии группы однофазных ЭП, которые распределены по фазам с неравномерностью не выше 15% по отношению к общей мощности трехфазных и однофазных ЭП в группе, они могут быть представлены в расчете как эквивалентная группа трехфазных ЭП с той же суммарной номинальной мощностью.
В случае превышения указанной неравномерности номинальная мощность эквивалентной группы трехфазных ЭП принимается равной тройному значению мощности наиболее загруженной фазы.
Остальное приходится додумывать самому, т.к. четких указаний по расчету не приводится. А как быть, когда разные коэффициенты использования и коэффициенты мощности, мощности ЭП отличаются значительно друг от друга?
После всех размышлений и общения со своими коллегами, я пришел к выводу, что однофазные ЭП следует приводить к трехфазной мощности с учетом эффективного числа ЭП и в результате мы должны получить эквивалент не одного, а N-го количества трехфазных ЭП, которые соответствуют мощности однофазных электроприемников нашего щита.
Внешний вид обновленной программы:
Расчет вводного устройства.
Расчет вводного устройстваРасчет распределительного щита.
Расчет распределительного щита.
Определение условной трехфазной мощности, создаваемой в трехфазной сети однофазными ЭП.
Определение условной трехфазной мощности, создаваемой в трехфазной сети однофазными ЭП.
Порядок расчета электрических нагрузок, в том числе и определение условной трехфазной мощности я расскажу в своем очередном видеоролике.
Жду ваших замечаний и предложений.
P.S. Я этой программой пользуюсь и при расчете административных зданий.
Условия получения программы смотрите на странице МОИ ПРОГРАММЫ.
Советую почитать:
Общие замечания к расчету трехфазных цепей
1. При расчете трехфазных цепей исходят из предположения, что генератор дает симметричную систему напряжений. На практике несимметрия нагрузки практически не влияет на систему напряжений генератора в том случае, если мощность нагрузки мала по сравнению с мощностью генератора или сети электроснабжения.
2. Схема соединения обмоток трехфазного генератора не предопределяет схему соединения нагрузки. Так, при соединении фаз генератора в звезду нагрузка может быть соединена в звезду с нейтральным проводом, в звезду без нейтрального провода или, наконец, в треугольник.
Мощность трехфазной цепи, ее расчет и измерение
В трехфазных цепях, так же как и в однофазных, пользуются понятиями активной, реактивной и полной мощностей.
Соединение потребителей звездой
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз
(3.23)
P = Pa + Pb + Pc,
где
(3.24)
Pa = Ua Ia cos φa; Pb = Ub Ib cos φb; Pc = Uc Ic cos φc; Ua, Ub, Uc; Ia, Ib, Ic – фазные напряжения и токи; φa, φb, φc – углы сдвига фаз между напряжением и током.Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз
(3.25)
Q = Qa + Qb + Qc,
где
(3.26)
Qa = Ua Ia sin φa; Qb = Ub Ib sin φb; Qc = Uc Ic sin φc.
Полная мощность отдельных фаз
(3.27)
Sa = Ua Ia;
S
Полная мощность трехфазного приемника
(3.28)
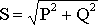 .
.
При симметричной системе напряжений (Ua = Ub = Uc = UФ) и симметричной нагрузке (Ia = Ib = Ic = IФ; φa = φb = φc = φ) фазные мощности равны Pa = Pb = Pc = PФ = UФ IФ cos φ; Qa = Qb = Qc = QФ = UФ IФ sin φ.
Активная мощность симметричного трехфазного приемника
(3.29)
P = 3 PФ = 3 UФ IФ cos φ.
Аналогично выражается и реактивная мощность
(3.30)
Q = 3 QФ = 3 UФ IФ sin φ.
Полная мощность
(3.31)
S = 3 SФ = 3 UФ IФ.
Отсюда следует, что в трехфазной цепи при симметричной системе напряжений и симметричной нагрузке достаточно измерить мощность одной фазы и утроить результат.
Соединение потребителей треугольником
В общем случае несимметричной нагрузки активная мощность трехфазного приемника равна сумме активных мощностей отдельных фаз
(3.32)
P = Pab + Pbc + Pca,
где
(3.33)
Pab = Uab Iab cos φab; Pbc = Ubc Ibc cos φbc; Pca = Uca Ica cos φca; Uab, Ubc, Uca; Iab, Ibc, Ica – фазные напряжения и токи; φab, φbc, φca – углы сдвига фаз между напряжением и током.
Реактивная мощность соответственно равна алгебраической сумме реактивных мощностей отдельных фаз
(3.34)
Q = Qab + Qbc + Qca,
где
(3.35)
Qab = Uab Iab sin φab; Qbc = Ubc Ibc sin φbc; Qca = Uca Ica sin φca.
Полная мощность отдельных фаз
(3.36)
Sab = Uab Iab; Sbc = Ubc Ibc; Sca = Uca Ica.
Полная мощность трехфазного приемника
(3.37)
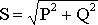 .
.
При симметричной системе напряжений (Uab = Ubc = Uca = UФ) и симметричной нагрузке (Iab = Ibc = Ica = IФ; φab = φbc = φca = φ) фазные мощности равны Pab = Pbc = Pca = PФ = UФ IФ cos φ; Qab = Qbc = Qca = QФ = UФ IФ sin φ.
Активная мощность симметричного трехфазного приемника
P = 3 PФ = 3 UФ IФ cos φ.
Аналогично выражается и реактивная мощность
Q = 3 QФ = 3 UФ IФ sin φ.
Полная мощность
S = 3 SФ = 3 UФ IФ.
Так как за номинальные величины обычно принимают линейные напряжения и токи, то мощности удобней выражать через линейные величины UЛ и IЛ.
При
соединении фаз симметричного приемника
звездой UФ = UЛ / 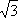 ,
IФ = IЛ,
при соединении треугольником
UФ = UЛ, IФ = IЛ /
,
IФ = IЛ,
при соединении треугольником
UФ = UЛ, IФ = IЛ / 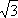 .
Поэтому независимо от схемы соединения
фаз приемника активная мощность при
симметричной нагрузке определяется
одной и той же формулой
.
Поэтому независимо от схемы соединения
фаз приемника активная мощность при
симметричной нагрузке определяется
одной и той же формулой
(3.38)
P
= 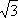 UЛ IЛ cos φ.
UЛ IЛ cos φ.
где UЛ и IЛ – линейное напряжение и ток; cos φ – фазный.
Обычно индексы «л» и «ф» не указывают и формула принимает вид
(3.39)
P
= 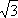 U
I cos φ.
U
I cos φ.
Соответственно реактивная мощность
(3.40)
Q
= 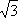 U
I sin φ.
U
I sin φ.
и полная мощность
(3.41)
S
= 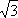 U
I.
U
I.
При этом надо помнить, что угол φ является углом сдвига фаз между фазными напряжением и током, и, что при неизмененном линейном напряжении, переключая приемник со звезды в треугольник его мощность увеличивается в три раза:
Δ P = Υ 3P.
Измерение активной мощности в трехфазных цепях
Измерение активной мощности в трехфазных цепях производят с помощью трех, двух или одного ваттметров, используя различные схемы их включения. Схема включения ваттметров для измерения активной мощности определяется схемой сети (трех- или четырехпроводная), схемой соединения фаз приемника (звезда или треугольник), характером нагрузки (симметричная или несимметричная), доступностью нейтральной точки.
При несимметричной нагрузке в четырехпроводной цепи активную мощность измеряют тремя ваттметрами (рис. 3.18), каждый из которых измеряет мощность одной фазы – фазную мощность.
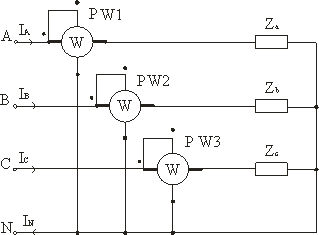
Рис. 3.18
Активная мощность приемника определяют по сумме показаний трех ваттметров
(3.42)
P = P1 + P2 + P3,
где P1 = UA IA cos φA; P2 = UB IB cos φB; P3 = UC IC cos φC.
Измерение мощности тремя ваттметрами возможно при любых условиях.
При симметричном приемнике и доступной нейтральной точке активную мощность приемника определяют с помощью одного ваттметра, измеряя активную мощность одной фазы PФ по схеме рис. 3.19. Активная мощность всего трехфазного приемника равна при этом утроенному показанию ваттметра: P = 3 PФ.
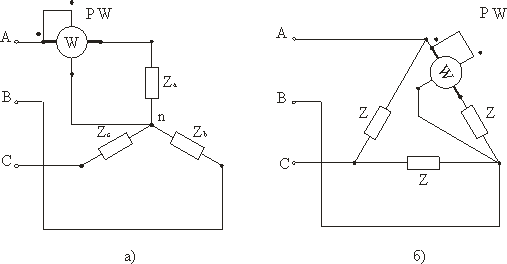
Рис. 3.19
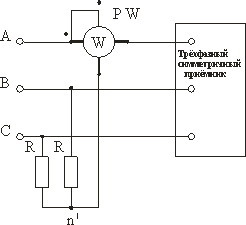
Рис. 3.20
На рис. 3.19 показано включение прибора непосредственно в одну из фаз приемника. В случае, если нейтральная точка приемника недоступна или зажимы фаз приемника, включенного треугольником не выведены, применяют схему рис. 3.20 с использованием искусственной нейтральной точки n’. В этой схеме дополнительно в две фазы включают резисторы с сопротивлением R = RV.
Измерение активной мощности симметричного приемника в трехфазной цепи одним ваттметром применяют только при полной гарантии симметричности трехфазной системы.
Измерение активной мощности двумя ваттметрами
В трехпроводных трехфазных цепях при симметричной и несимметричной нагрузках и любом способе соединения приемников широко распространена схема измерения активной мощности приемника двумя ваттметрами (рис. 3.21). Показания двух ваттметров при определенной схеме их включения позволяют определить активную мощность трехфазного приемника, включенного в цепь с симметричным напряжением источника питания.
На рис. 3.21 показана одна из возможных схем включения ваттметров: здесь токовые катушки включены в линейные провода с токами IA и IB, а катушки напряжения – соответственно на линейные напряжения UAC и UBC.
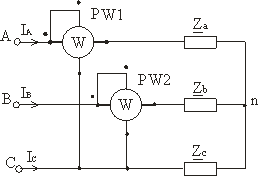
Рис. 3.21
Докажем, что сумма показаний ваттметров, включенных по схеме рис. 3.21, равна активной мощности Р трехфазного приемника. Мгновенное значение общей мощности трехфазного приемника, соединенного звездой,
(3.43)
p = uA iA + uB iB + uC iC.
Так как
(3.44)
iA + iB + iC = 0.
то
(3.45)
iC = -(iA + iB).
Подставляя значение iC в выражение для р, получаем
(3.46)
p = uA iA + uB iB — uC (iA + iB) = (uA — uC) iA + (uB — uC) iB = uAC iA + uBC iB.
Выразив мгновенные значения u и i через их амплитуды, можно найти среднюю (активную) мощность
(3.47)
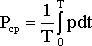 ,
,
которая составит
(3.48)
P = UAC IA cos(UAC^IA) + UBC IB cos(UBC^IB) = P1 + P2.
Так как UAC, UBC, IA и IB – соответственно линейные напряжения и токи, то полученное выражение справедливо и при соединении потребителей треугольником.
Следовательно, сумма показаний двух ваттметров действительно равна активной мощности Р трехфазного приемника.
При симметричной нагрузке
IA = IB = IЛ, UAC = UBC = UЛ.
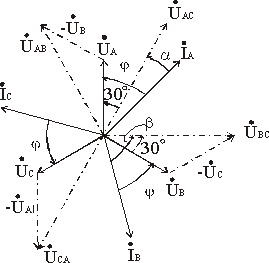
Рис. 3.22
Из векторной диаграммы (рис. 3.22) получаем, что угол α между векторами UAC и IA равен α = φ — 30°, а угол β между векторами UBC и IB составляет β = φ + 30°.
В рассматриваемом случае показания ваттметров можно выразить формулами
(3.49)
P1 = UЛ IЛ cos(φ — 30°),
(3.50)
P2 = UЛ IЛ cos(φ + 30°).
Сумма показаний ваттметров
(3.51)
P1 + P2 = UЛ IЛ [cos(φ — 30°) + cos(φ + 30°)] = 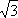 UЛ IЛ cos φ.
UЛ IЛ cos φ.
Ввиду того, что косинусы углов в полученной формуле могут быть как положительными, так и отрицательными, в общем случае активная мощность приемника, измеренная по методу двух ваттметров, равна алгебраической сумме показаний.
При симметричном приемнике показания ваттметров Р1 и Р2 будут равны только при φ = 0°. Если φ > 60°, то показания второго ваттметра Р2 будет отрицательным.
Для измерения активной мощности в трехфазных цепях промышленных установок широкое применение находят двухэлементные трехфазные электродинамические и ферродинамические ваттметры, которые содержат в одном корпусе два измерительных механизма и общую подвижную часть. Катушки обоих механизмов соединены между собой по схемам, соответствующим рассмотренному методу двух ваттметров. Показание двухэлементного ваттметра равно активной мощности трехфазного приемника.
Лицензия | Model.Exponenta.Ru | Jigrein |
|
|
© Н.В. Клиначёв, 1999-2008. Все права защищены. 800×600.
Расчет трехфазных цепей (Лекция №17)
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если . В противном случае они являются несимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии: .
Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол . Вследствие указанного расчет таких цепей проводится для одной – базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.
Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз можно записать
,
где определяется характером нагрузки .
Тогда на основании вышесказанного
;
.
Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда» .
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении необходимо определить линейные токи и в схеме на рис. 3, все сопротивления в которой известны.
В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь , .
Тогда для тока можно записать
,
и соответственно .
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома
; ; .
По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:
.
Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений, строим треугольник (см. рис.5), из которого (путем замера) определяем значения углов a и b.
Тогда
Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке ей в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки источника и приемника занимают разные положения, т.е. .
Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке, что наглядно иллюстрирует векторная диаграмма на рис. 6,б.
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:
.
Тогда для искомых токов можно записать:
.
Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
| . | (1) |
При наличии нейтрального провода с нулевым сопротивлением , и из (1) . В случае отсутствия нейтрального провода . При симметричной нагрузке с учетом того, что , из (1) вытекает .
В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если .
Запишем выражения комплексных сопротивлений фаз нагрузки:
Тогда для напряжения смещения нейтрали будем иметь
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)
Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например, и . Тогда, поскольку при этом , соотношение (1) трансформируется в формулу
| . | (2) |
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- Какой многофазный приемник является симметричным?
- Какой режим работы трехфазной цепи называется симметричным?
- В чем заключается специфика расчета симметричных режимов работы трехфазных цепей?
- С помощью каких приемов трехфазная симметричная схема сводится к расчетной однофазной?
- Что такое напряжение смещения нейтрали, как оно определяется?
- Как можно определить комплексы линейных напряжений, если заданы их модули?
- Что обеспечивает нейтральный провод с нулевым сопротивлением?
- В цепи на рис. 6,а ; ; ; . Линейное напряжение равно 380 В.
- В схеме предыдущей задачи ; . Остальные параметры те же.
- В задаче 8 нейтральный провод оборван.
- В задаче 9 нейтральный провод оборван.
Определить ток в нейтральном проводе.
Ответ: .
Определить ток в нейтральном проводе.
Ответ: .
Определить фазные напряжения на нагрузке.
Ответ: ; ; .
Определить фазные напряжения на нагрузке.
Ответ: ; ; .
9.4. Расчет трехфазных цепей с несимметричной нагрузкой
Исходными данными являются:
— схема трехфазной цепи;
— фазные ЭДС генератора;
— сопротивления фаз несимметричной нагрузки.
Искомыми величинами являются токи и напряжения отдельных участков схемы.
Обмотки генератора и сопротивления нагрузки соединены в звезду с нулевым проводом
(рис. 9.29).
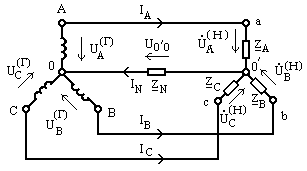
Рис. 9.29
Напряжение между нейтральными точками нагрузки и генератора, называемое напряжением
смещения нейтрали, найдем по методу двух узлов
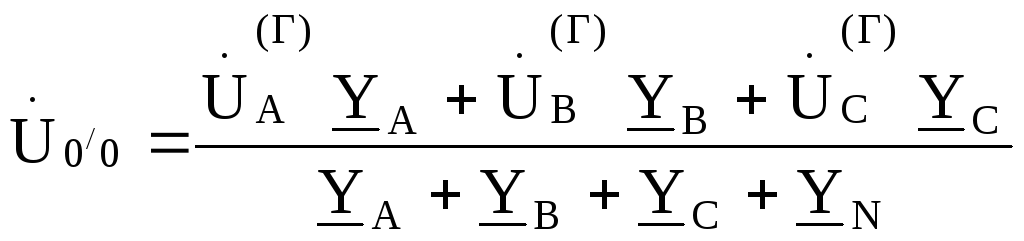 ,
,
где 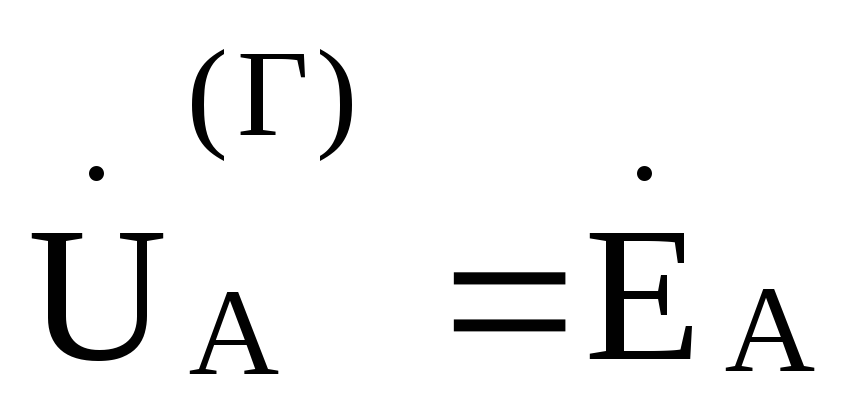 ,
,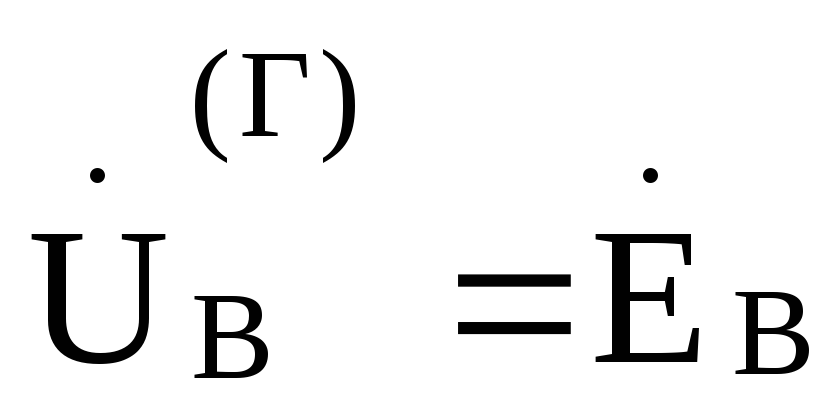 ,
,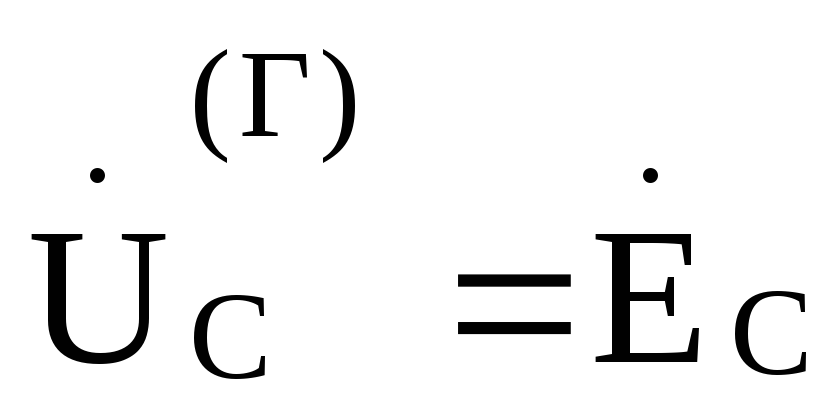 .
.
На основании обобщенного закона Оманайдем токи:
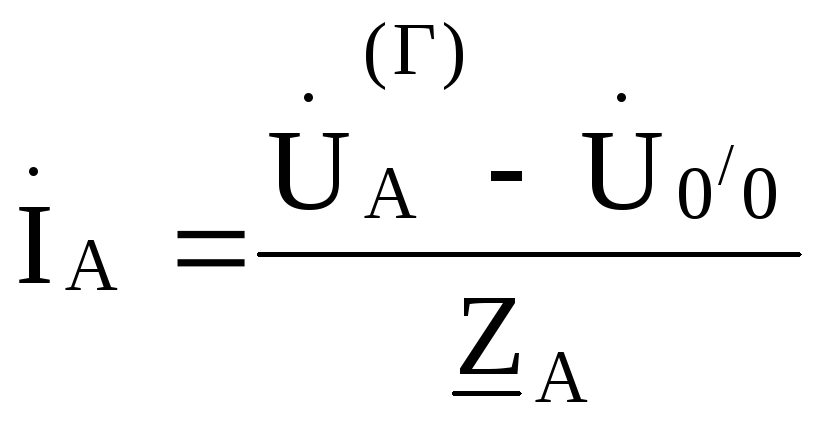 ,
,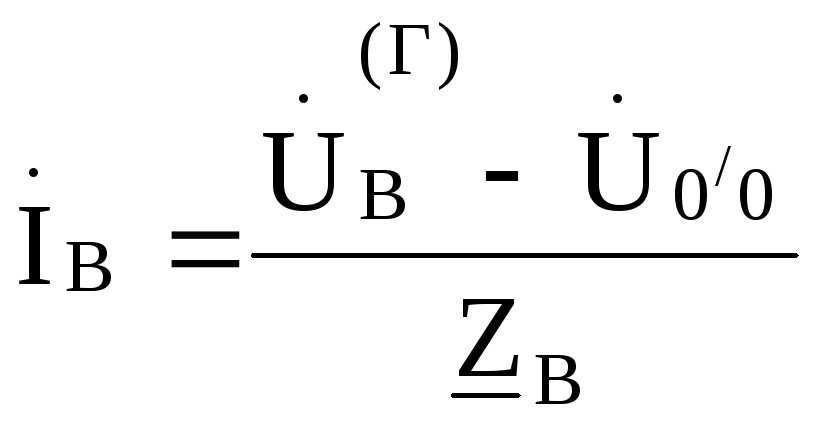 ,
,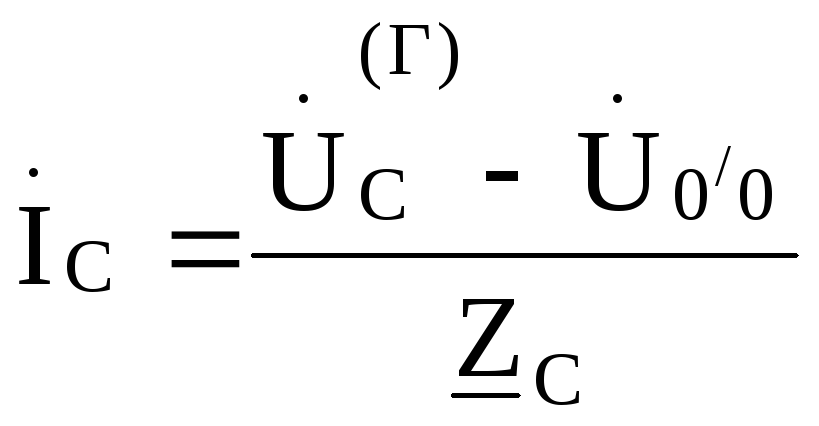
Ток в нулевом проводе
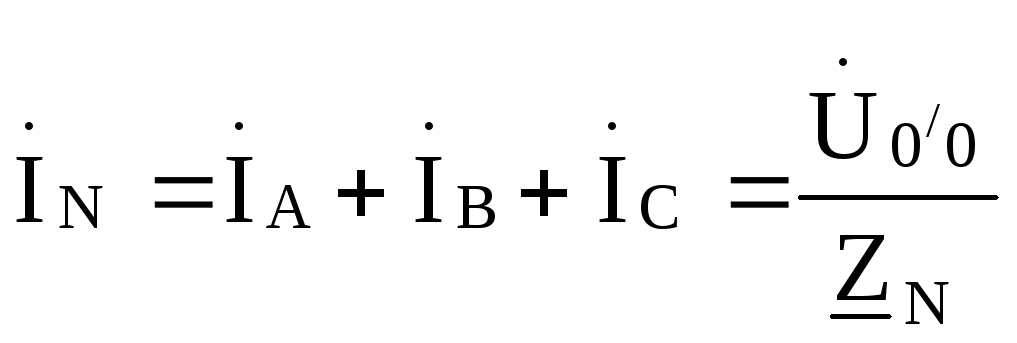
Если сопротивление нулевого провола,
равно нулю (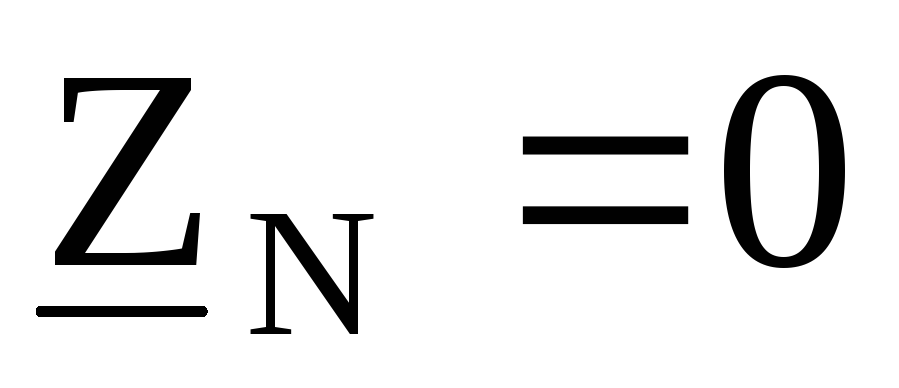 ),
то напряжение смещения нейтрали
),
то напряжение смещения нейтрали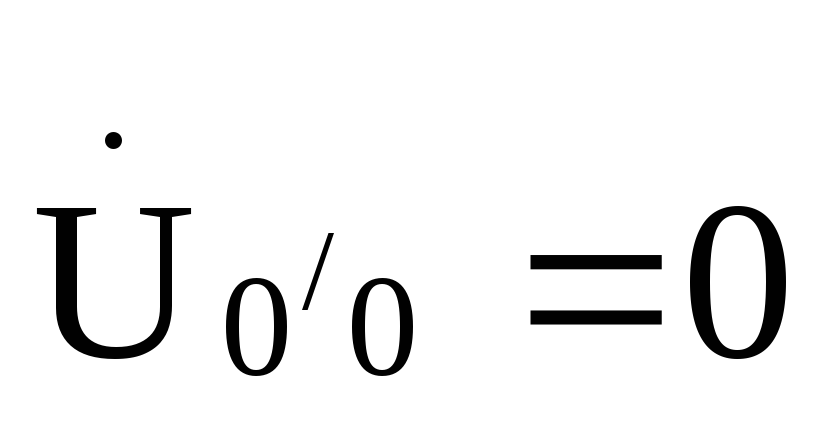 и
и
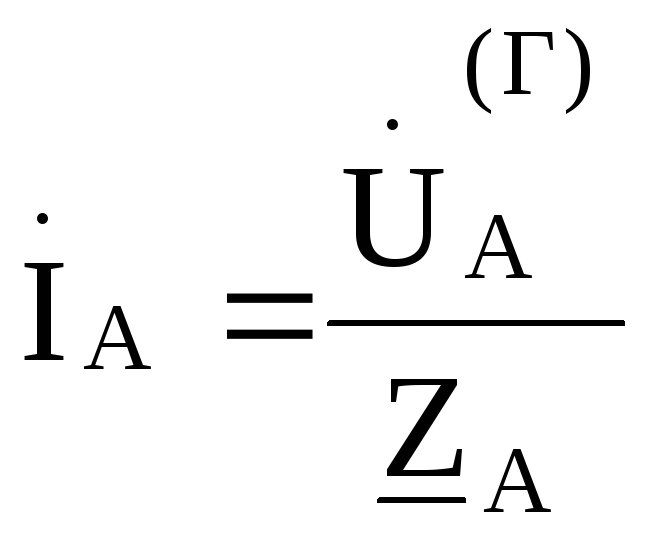 ,
,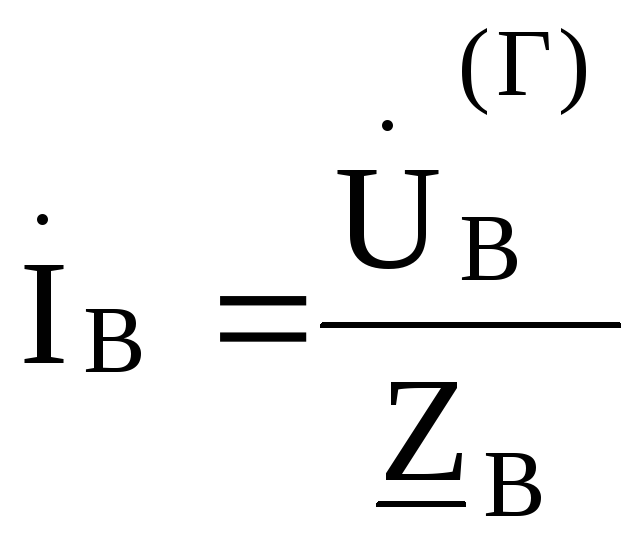 ,
,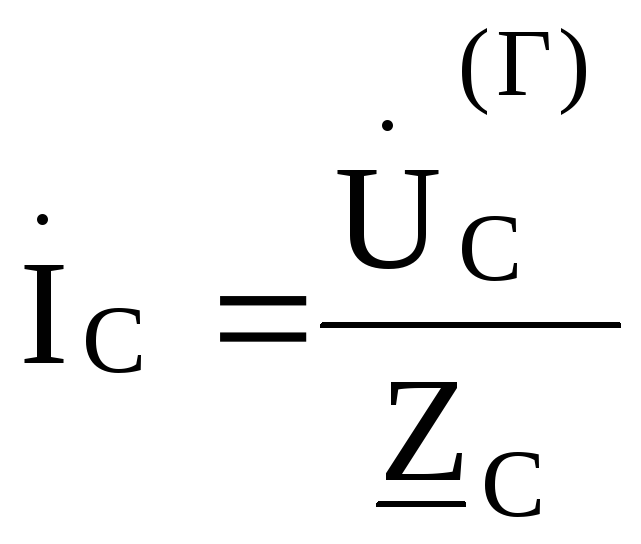
В этом случае фазные напряжения нагрузки иуяут равны соответствующим фазнымнапряжениям генератора и не будут зависеть от величины сопротивления в фазах нагрузки. Такой режим работы чаще всего встречается при питании однофазных приемников.
Если 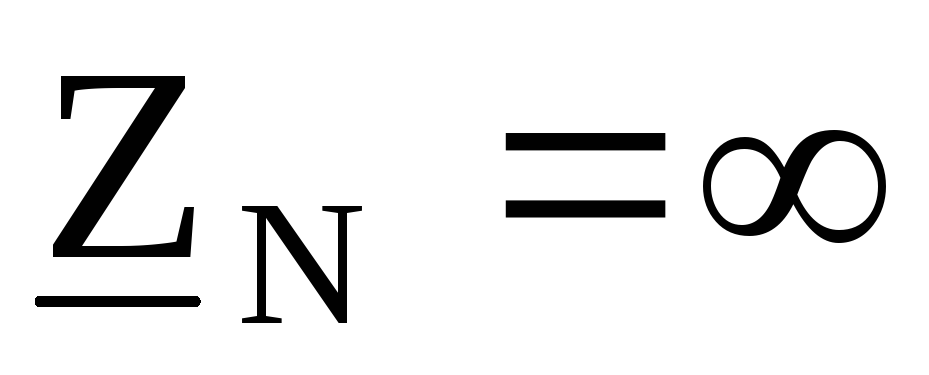 ,
то
,
то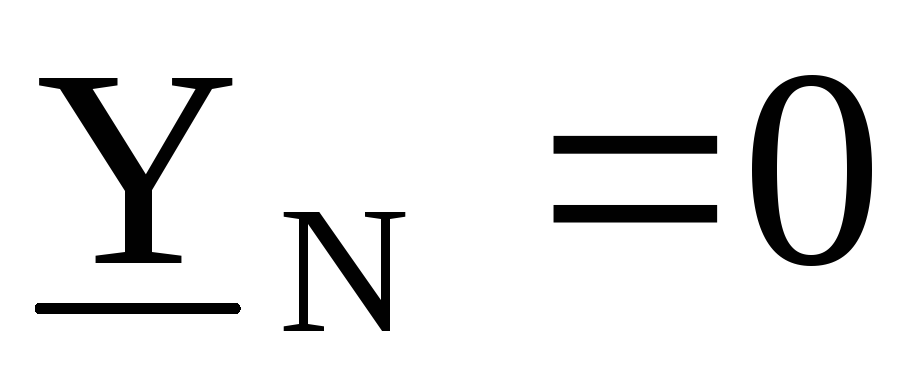 и
и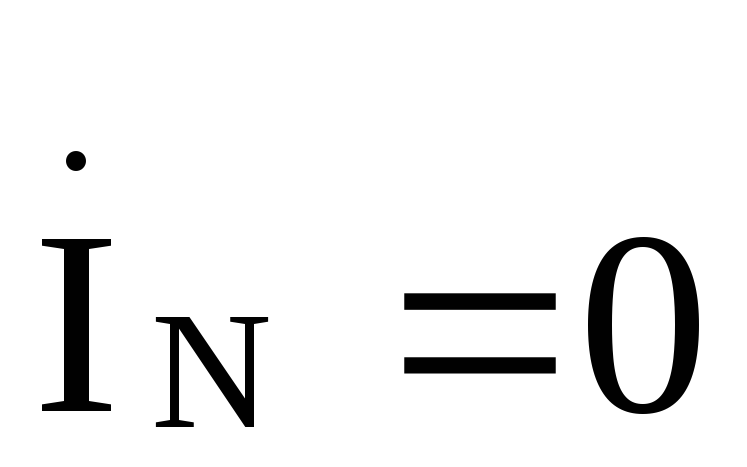 .
В этом случае напряжения на фаззах
нагрузки могут существенно отличаться
от номинальных напряжений, что
нежелательно. Приведем пример для
этого случая.
.
В этом случае напряжения на фаззах
нагрузки могут существенно отличаться
от номинальных напряжений, что
нежелательно. Приведем пример для
этого случая.
Пример 9.6.Для цепи рис. 9.30определить напряжения в фазах нагрузки и токи
при 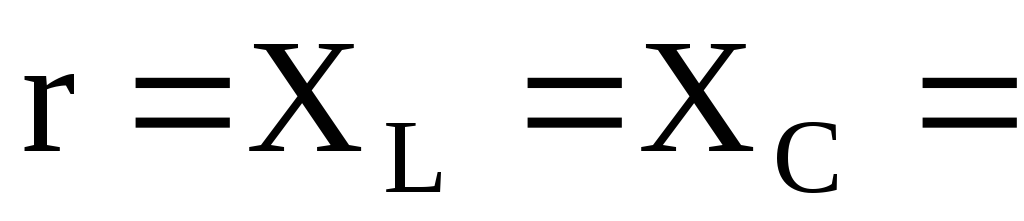 2 Ом.
2 Ом.
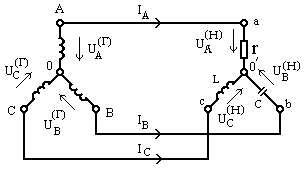
Рис. 9.30.
Фазное напряжение генератора 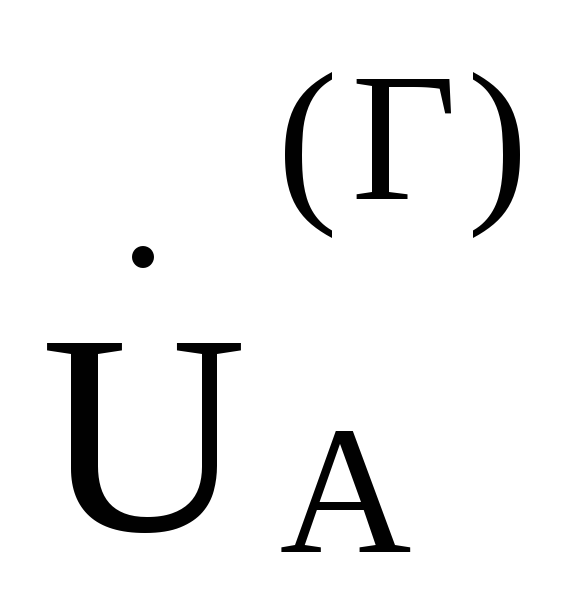 =220В.
=220В.
Решение
Найдем смещение нейтрали
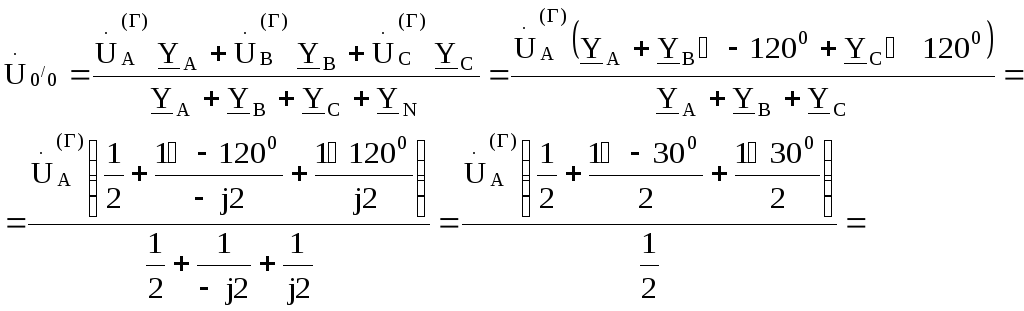
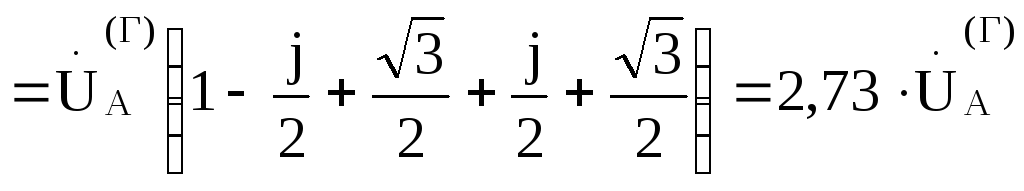
Тогда:
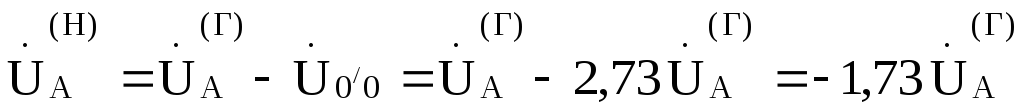 ;
;
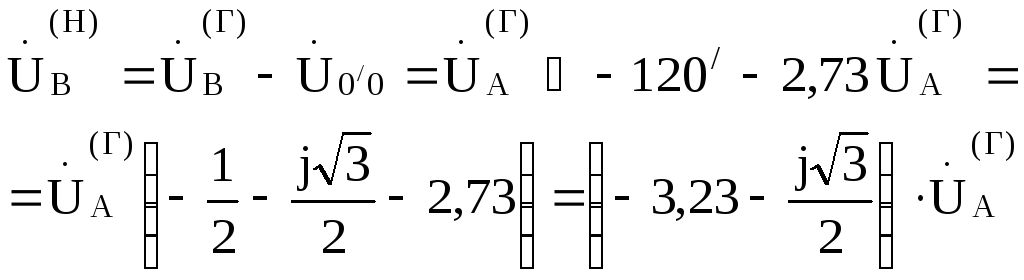 ;
;
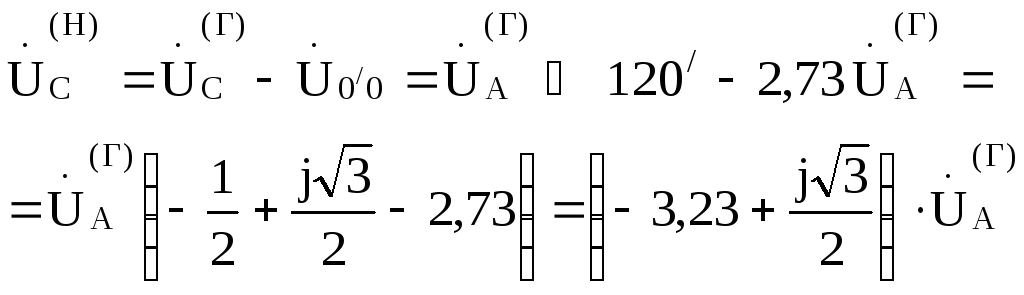 .
.
Считая 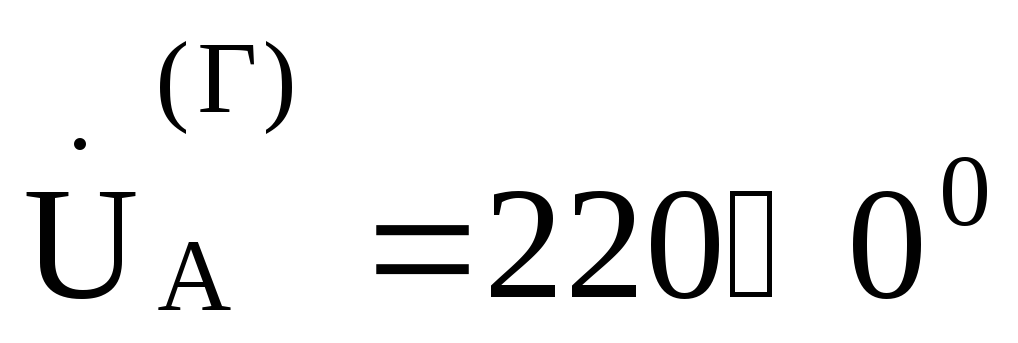 В, найдем токи:
В, найдем токи:
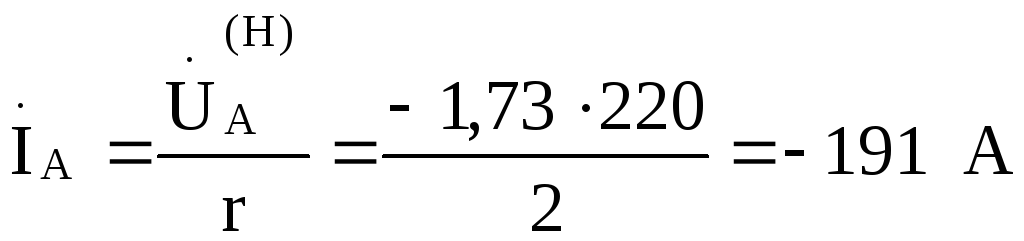
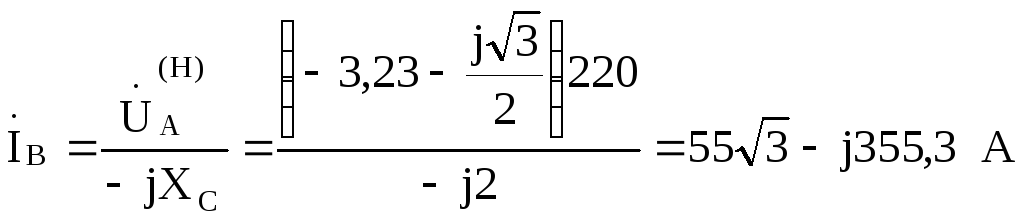
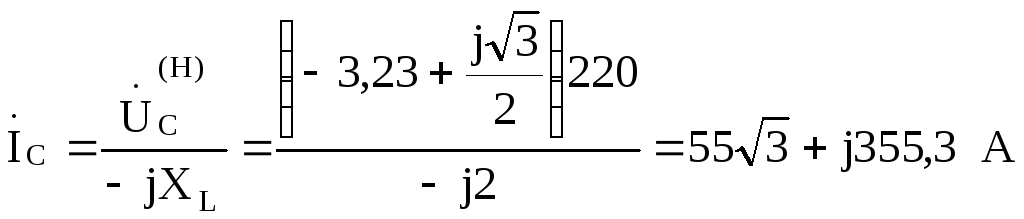
По найденным величинам построим векторно-топографическую диаграмму, показанную
на рис. 9.31.
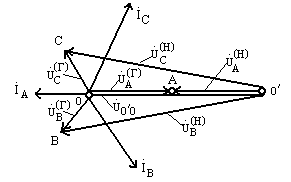
Рис. 9.31
2.Обмотки генератора и сопротивления нагрузки соединены в треугольник (рис. 9.32).
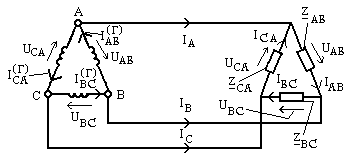
Рис. 9.32 Фазные токи нагрузки определяются по формулам
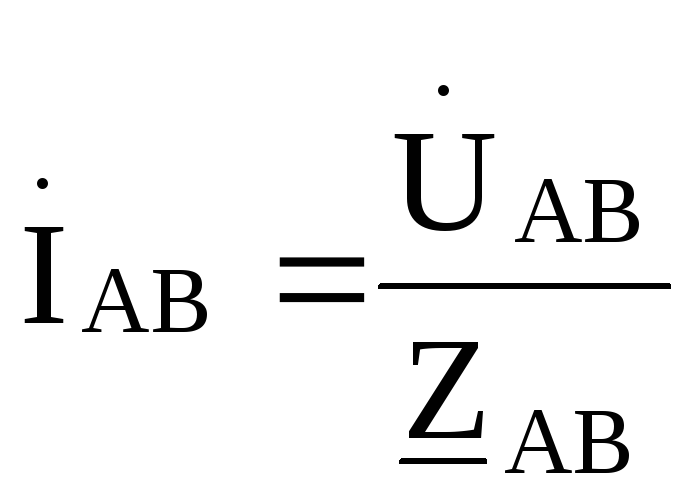
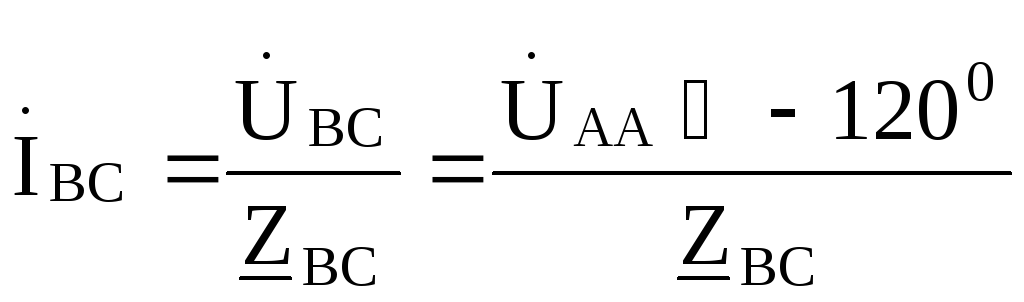
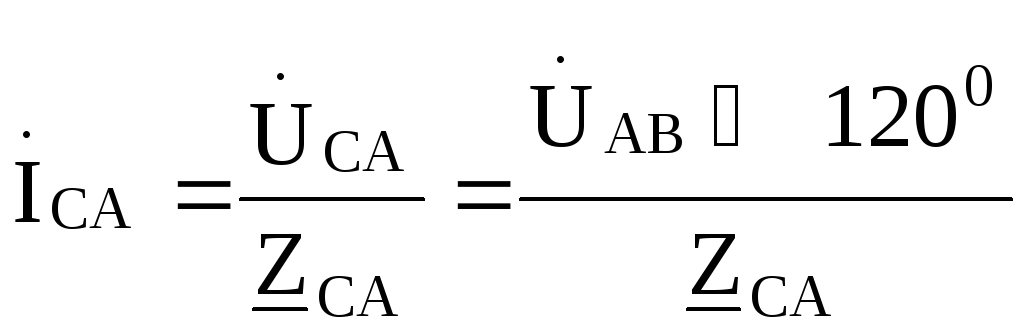
Токи в линиях (линейные токи):
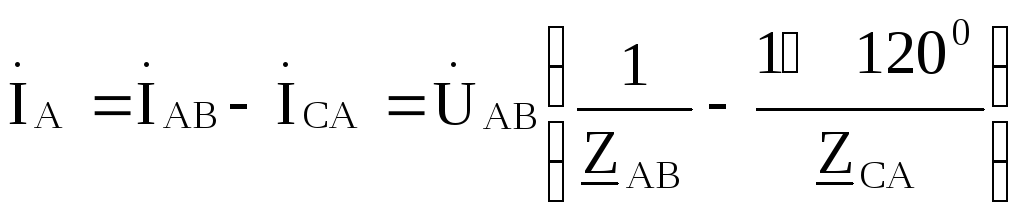
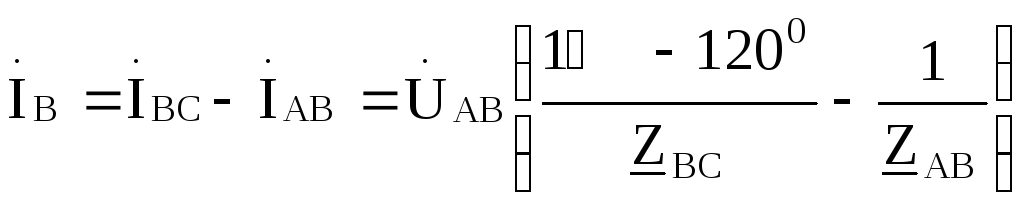
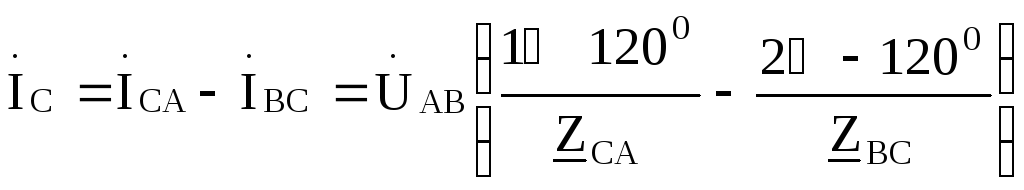
С помощью метода контурных токов можно показать, что фазные токи генератора оказываются равными соответствующим фазным токам нагрузки, т .е.
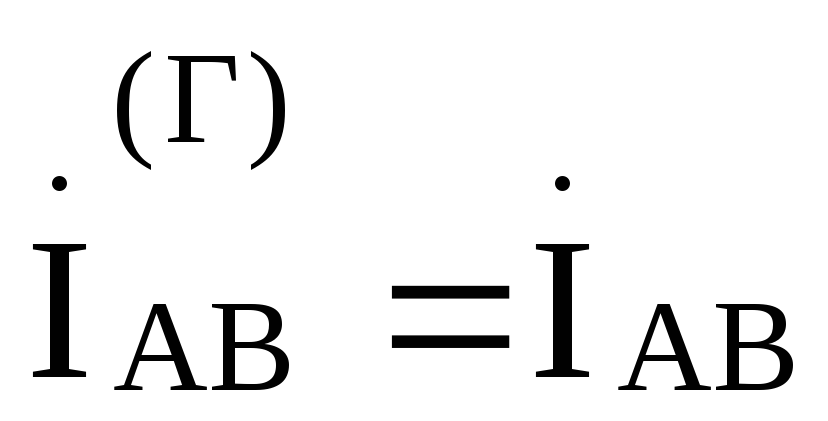 ,
,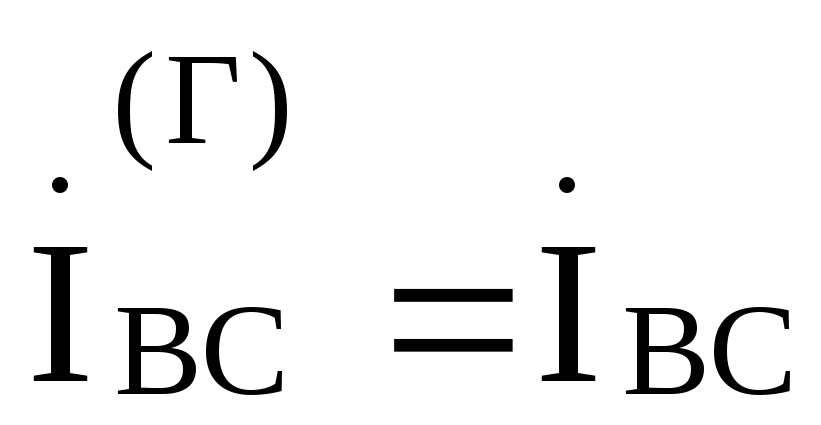 ,
,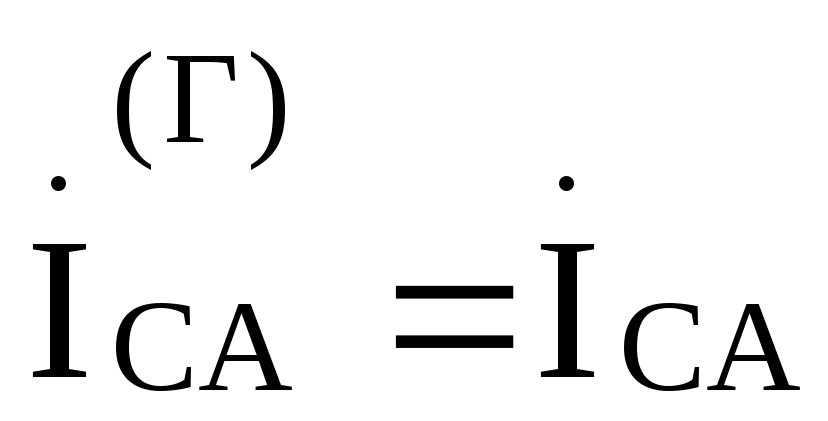
Пример 9.7.В цепи рис. 9.33определить фазные и линейные токи и построить векторно —
топографическую диаграмму.
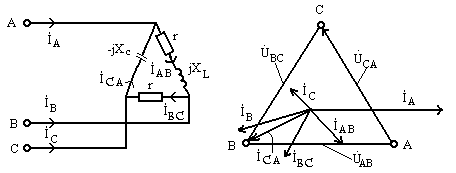
Рис. 9.33Рис. 9.34
если 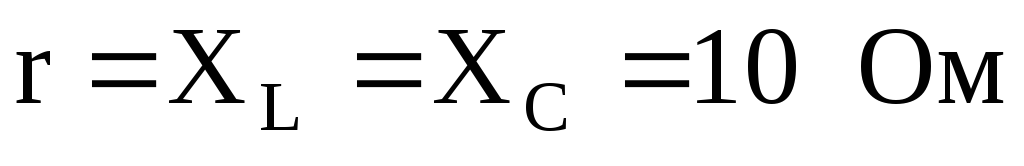 и фазное напряжение генератора обмотки
которого соединены в
и фазное напряжение генератора обмотки
которого соединены в
треугольник, равно 380В.
Решение
Принимаем 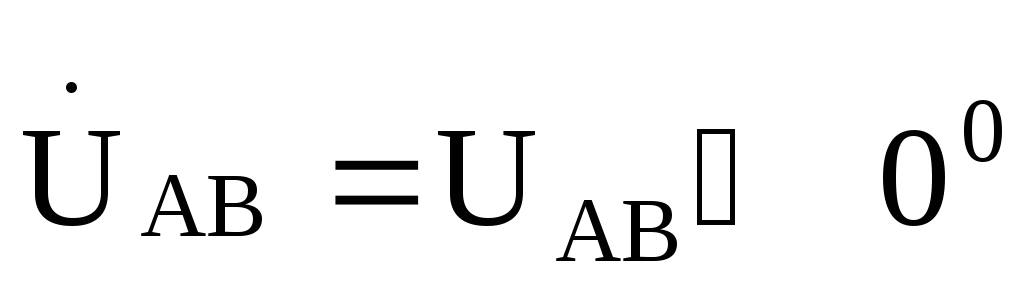 ,
тогда фазные токи нагрузки будут
,
тогда фазные токи нагрузки будут
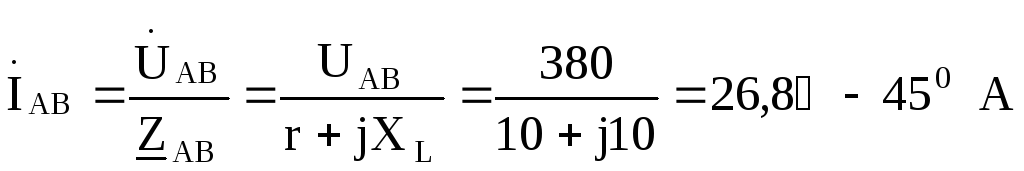
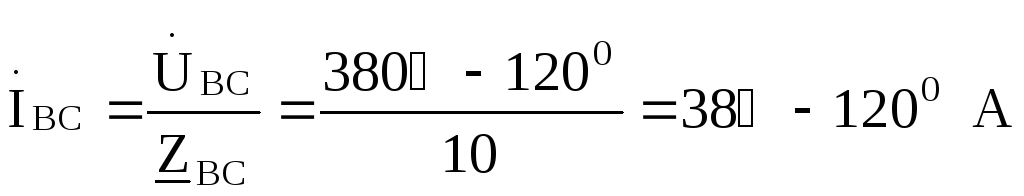
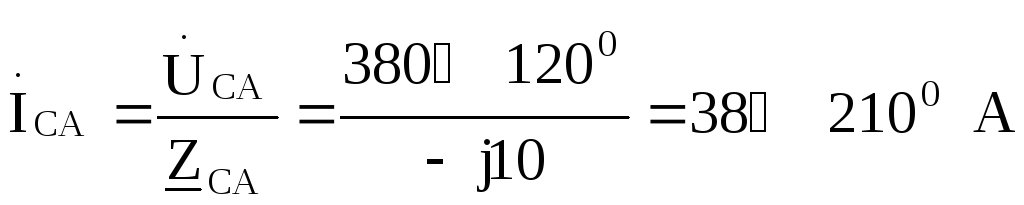
Линейные токи выражаем через фазные:

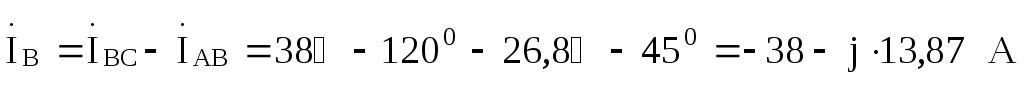

.
Векторно-топографическая диаграмма приведена на рис. 9.34.
3.Смешанное соединение сопротивлений нагрузки (cм.рис. 9.35).
Рис.9.35 Рис. 9.36
Линейные напряжения на зажимах генератора
в зависимости от способа соединения
его обмоток могут отличаться в 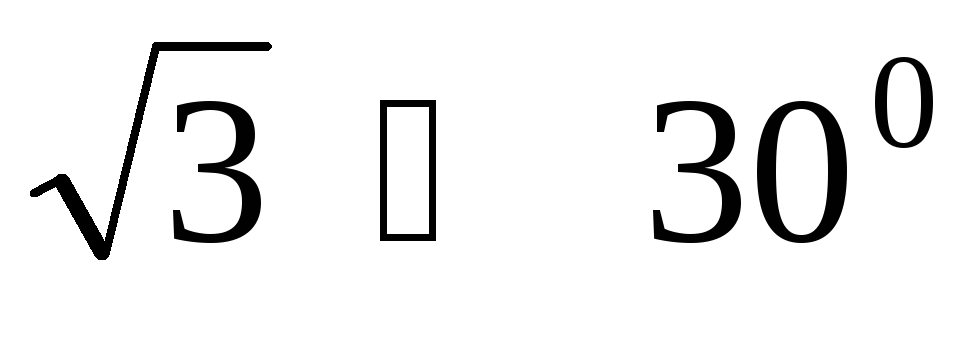 раз от соответствующих фазных напряжений.
Способ
раз от соответствующих фазных напряжений.
Способ
соединения обмотокгенератора иногда на схеме не указывают, тогда обязательно задается его
линейное напряжение, хотя бы по модулю. Для расчета токов в линии неснмметричную нагрузку
со смешанным соединением сопротивленнй преобразуют к единственной звезде или
единственному треугольнику, в которых токи в каждой фазе находятся известными приемами.
Например, в схеме рис. 9.35треугольник сопротивлений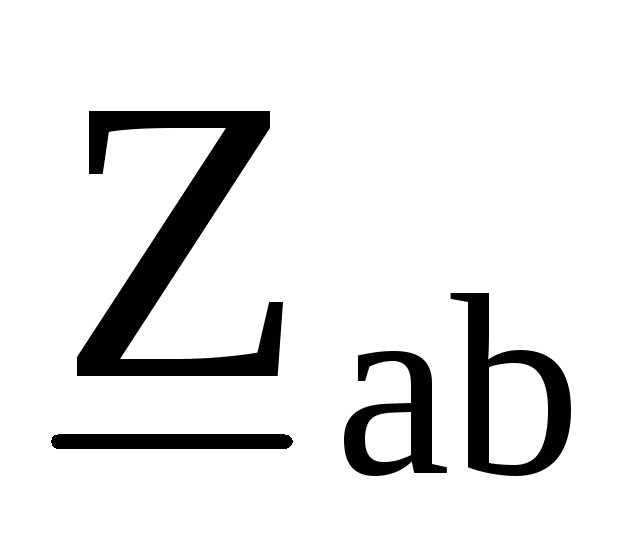 ,
,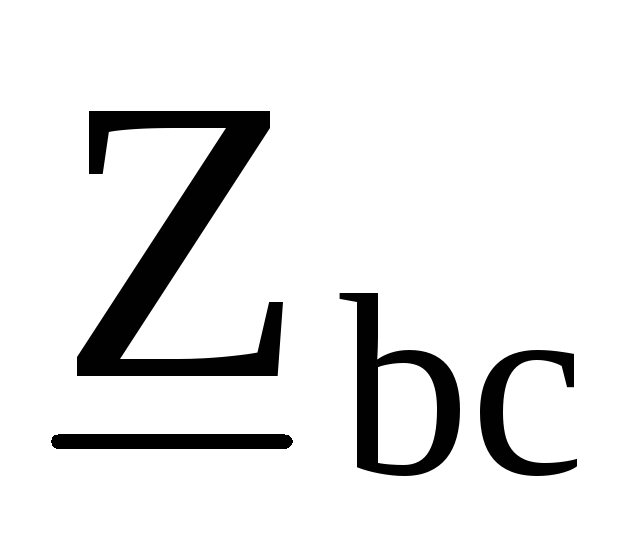 ,
,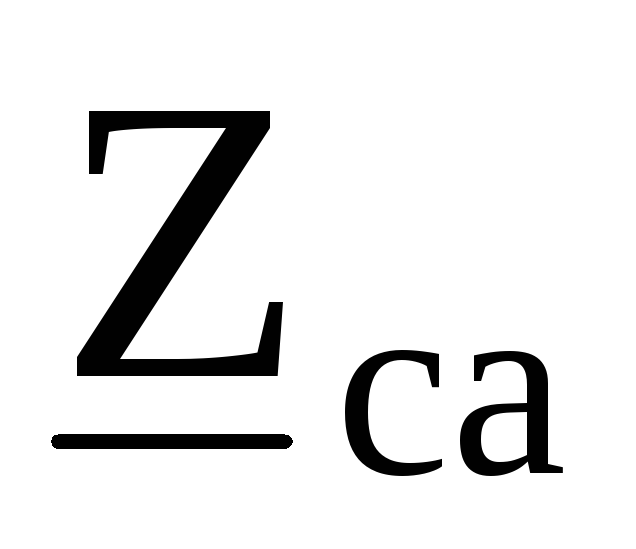 преобразуется
в
преобразуется
в
эквивалентную звезду с сопротивлениями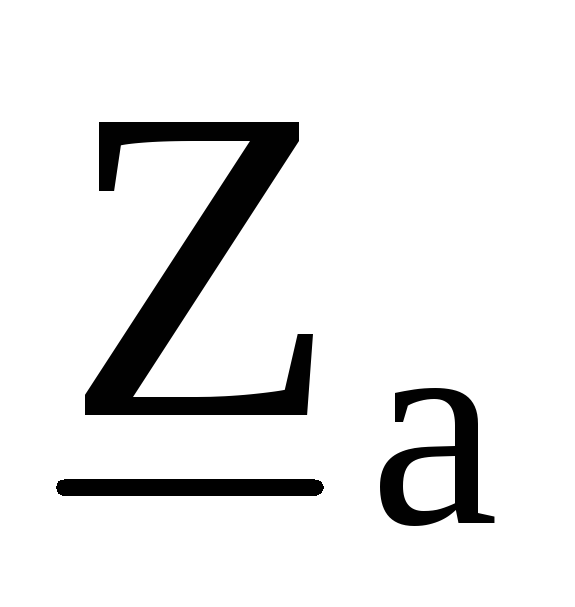 ,
,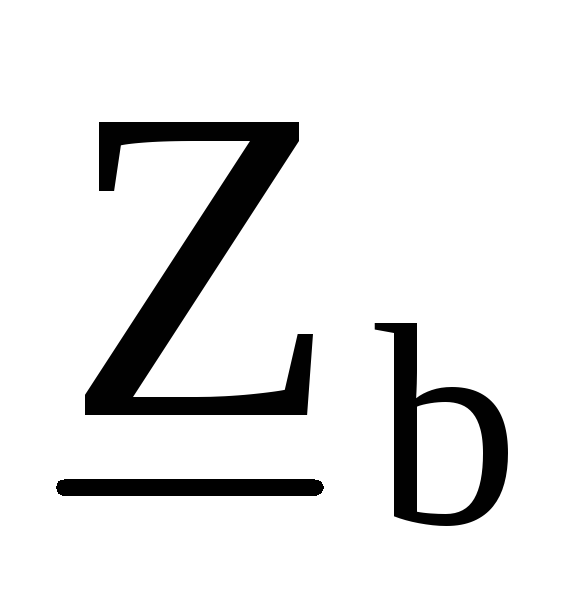 ,
,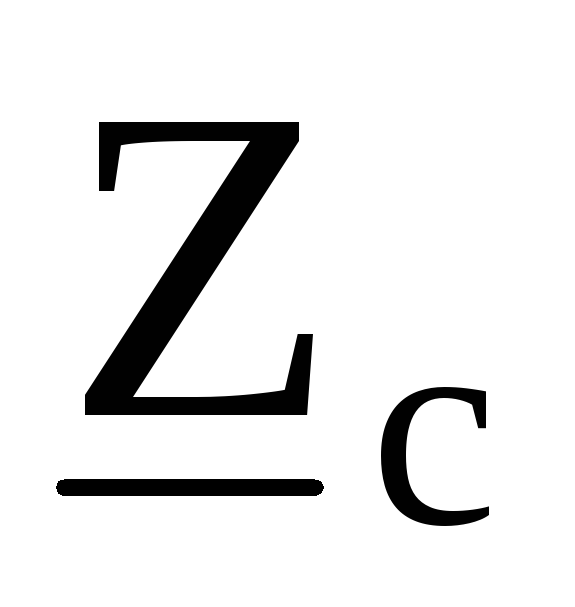 .
.
Полученные сопротивления:
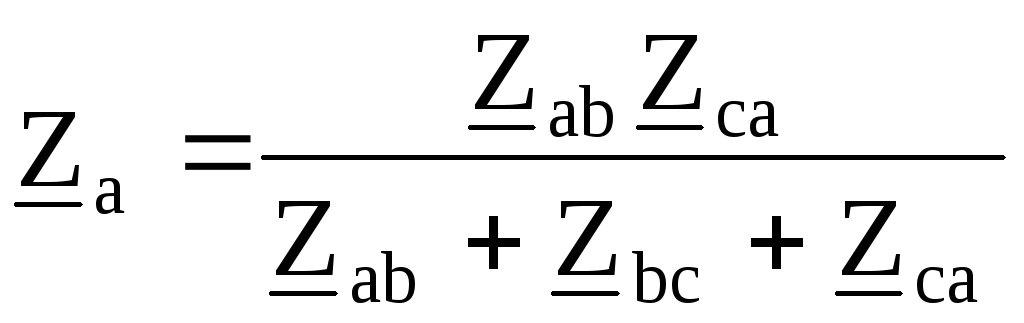 ;
;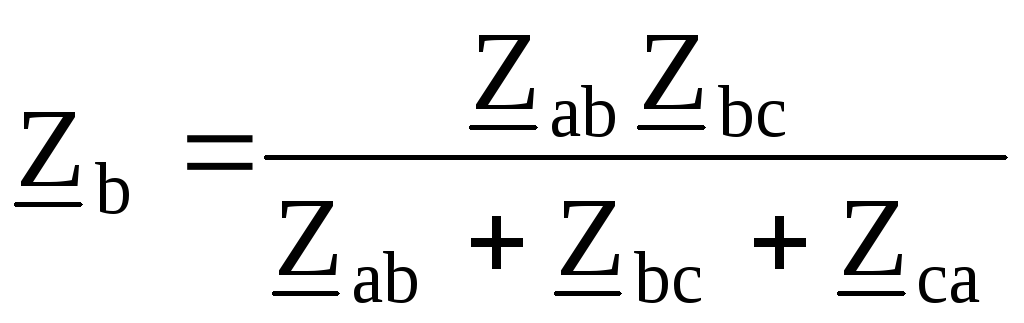 ;
;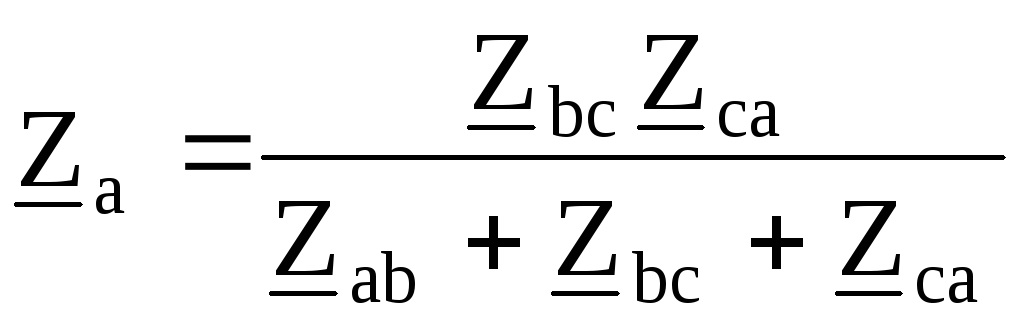 ;
;
объединяются с соответствующими
сопротивлениями 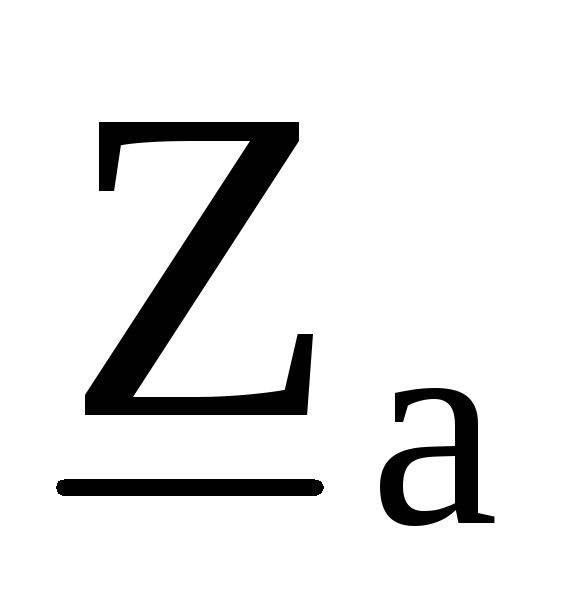 ,
,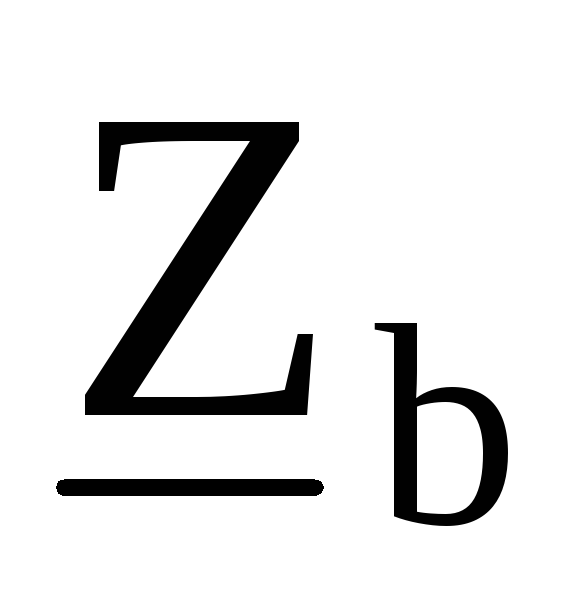 ,
,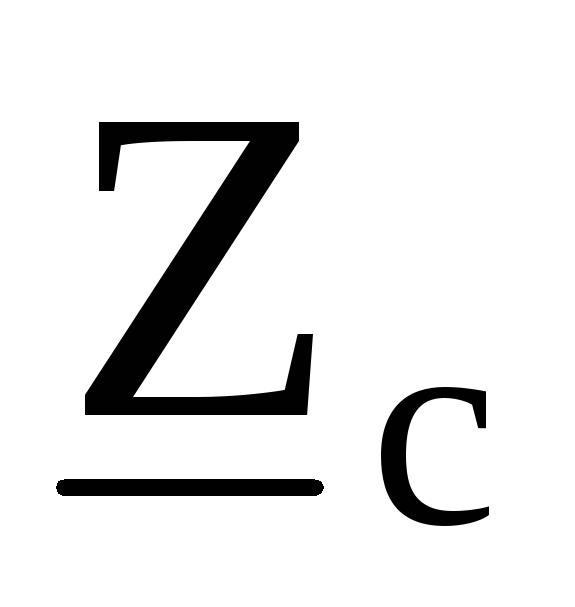 в результате чего получается
в результате чего получается
несимметричная звезда, показанная на рис. 9.36.Для этой звезды можно найти смещение
нейтрали нагрузки по отношению к «центру тяжести »треугольника линейных напряжений
генератора по формуле
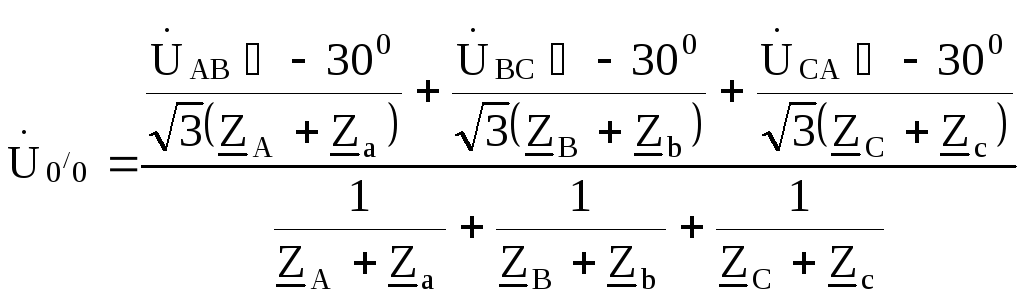
Тогда фазные напряжения на нагрузке будут
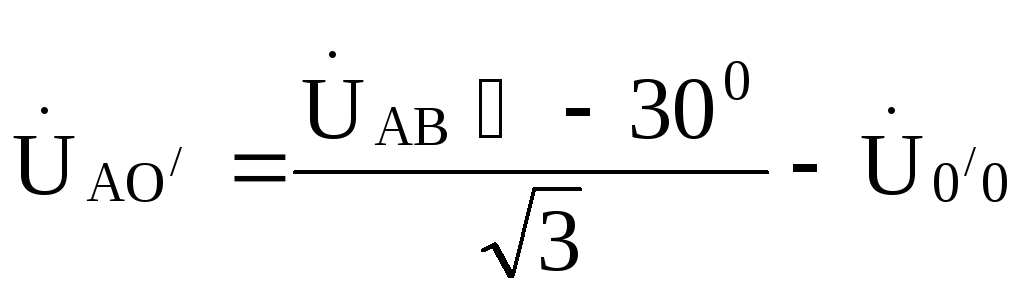 ;
;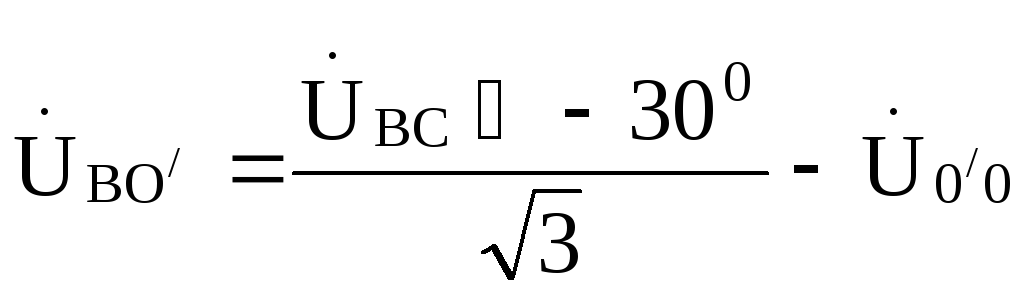 ;.
;.
По этим напряжениям находим токи
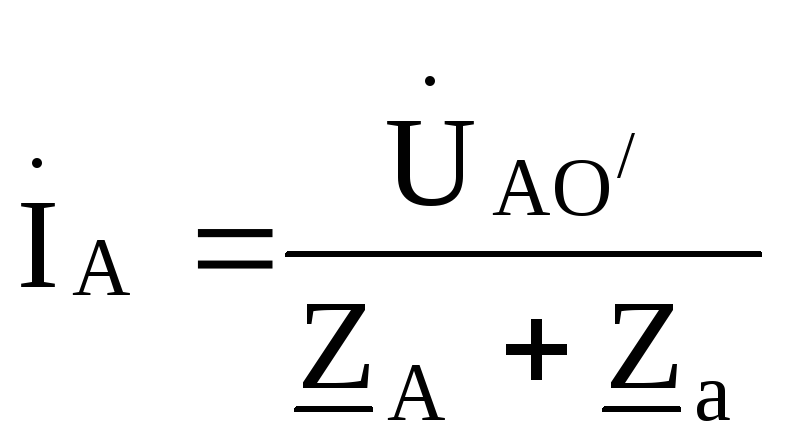 ;
;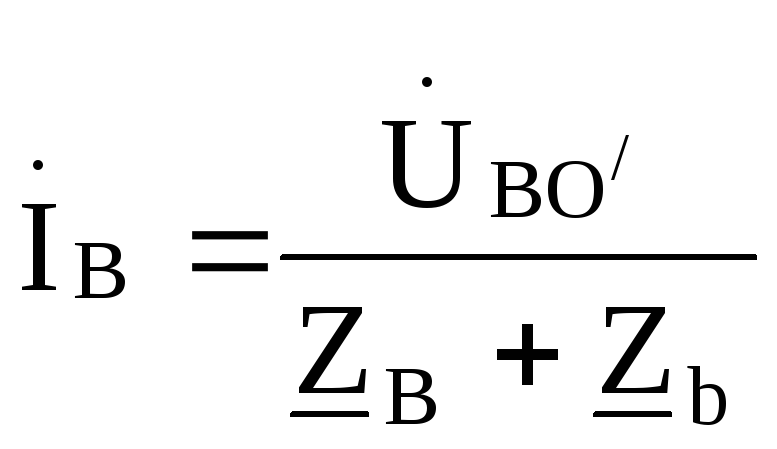 ;
;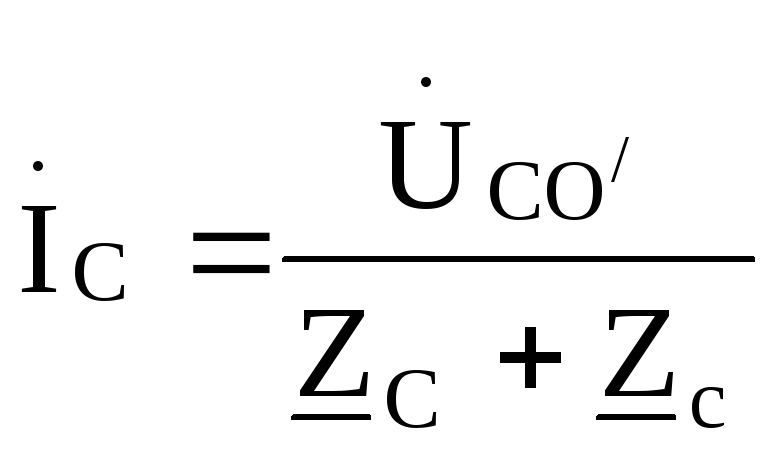 ;
;
По найденным токам ,
, ,
,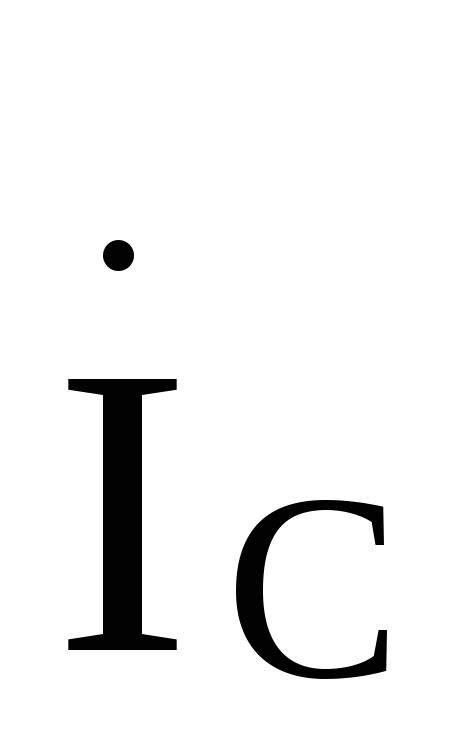 ,
находим напряжения на фазах звезды
с
,
находим напряжения на фазах звезды
с
сопротивлениями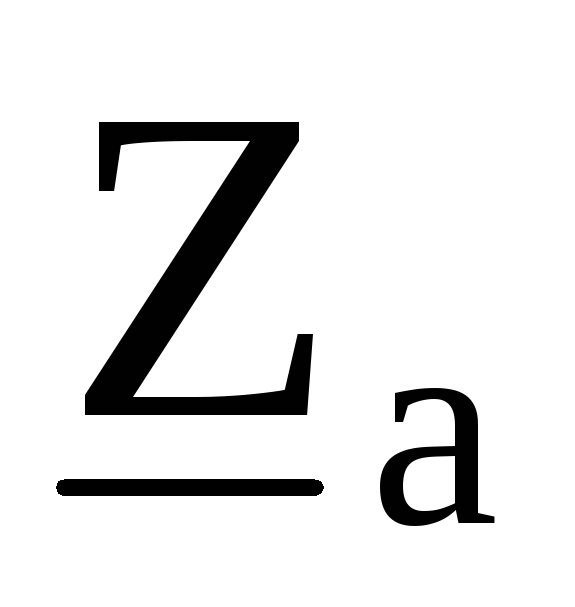 ,
,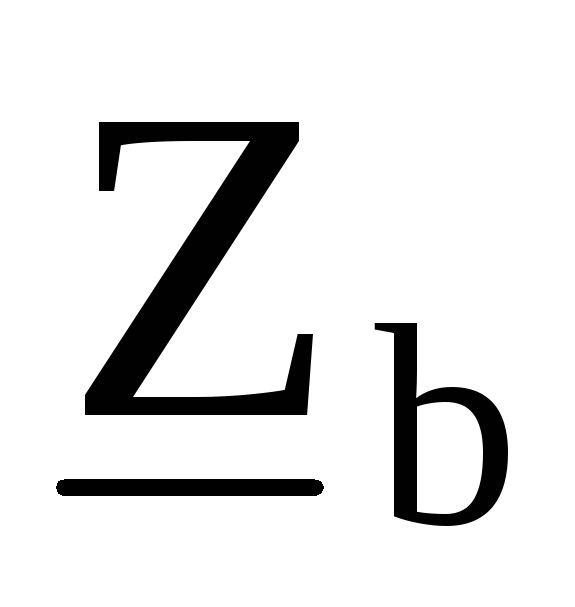 ,
,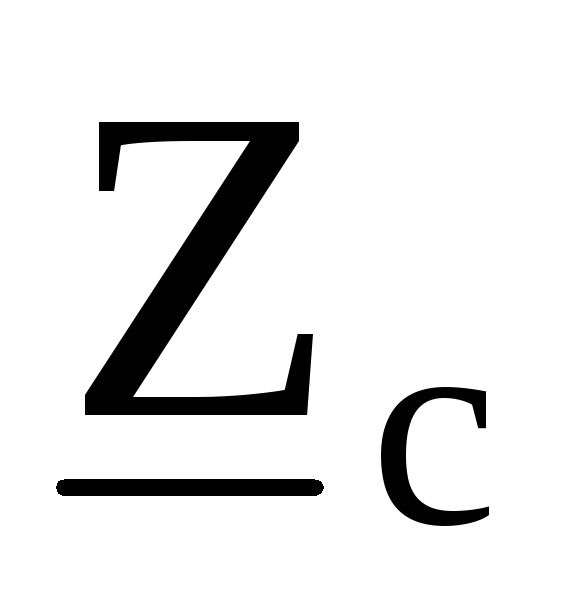 .
.
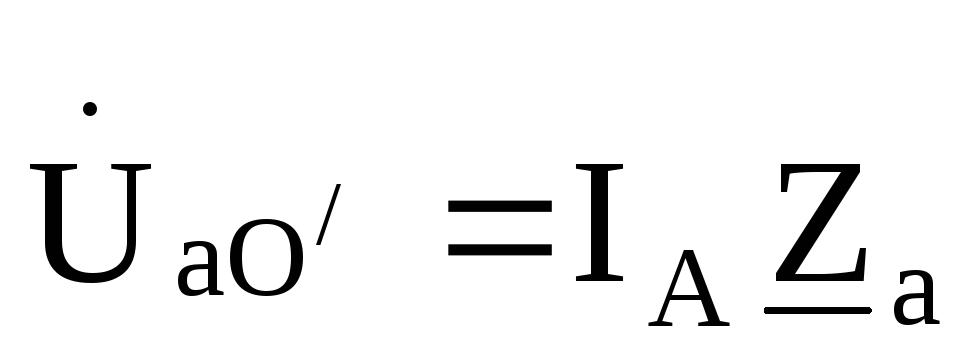 ,
,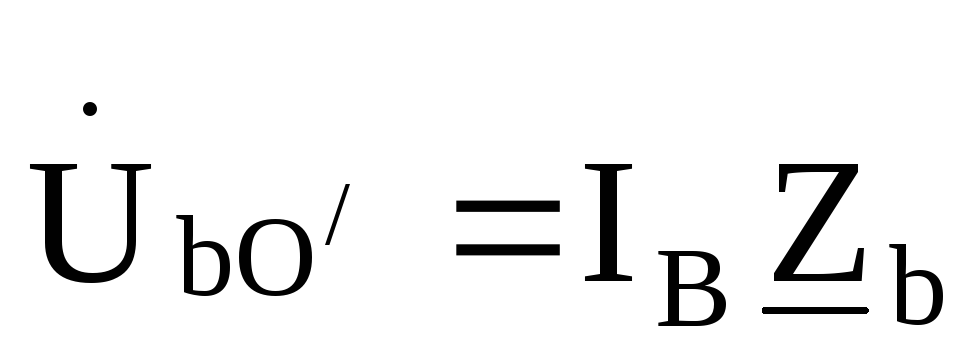 ,
,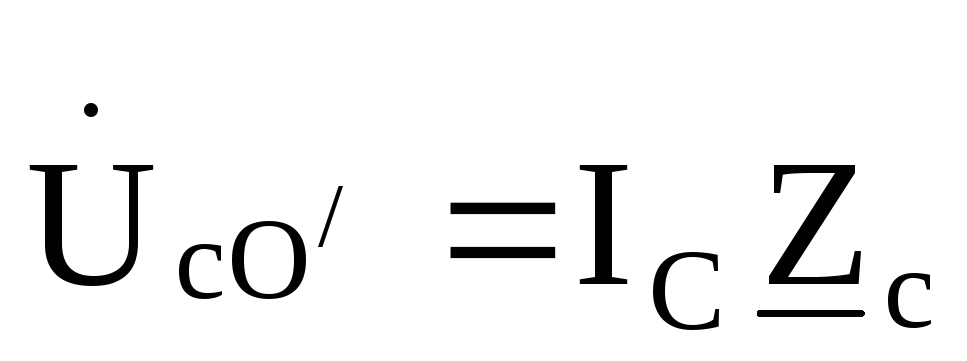 .
.
По этим фазным напряжениям находим напряжения зажимах треугольника
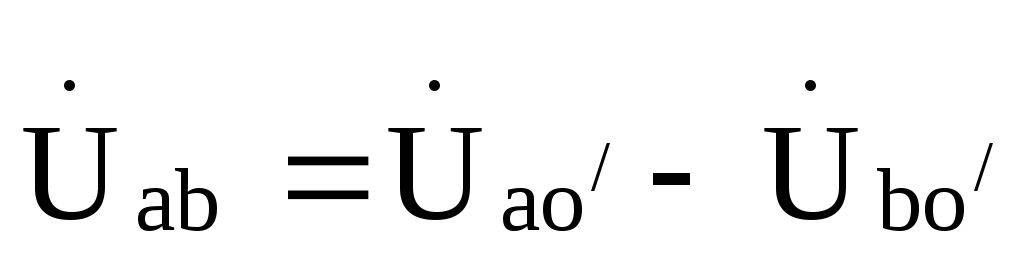 ,
,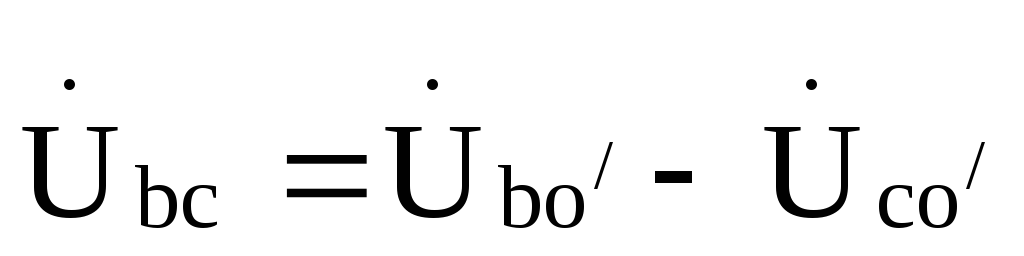 ,
,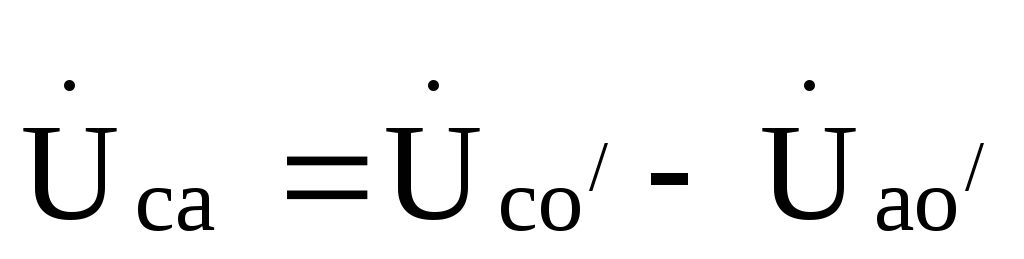 ,
,
Токи в фазах
треугольника находятся из выражений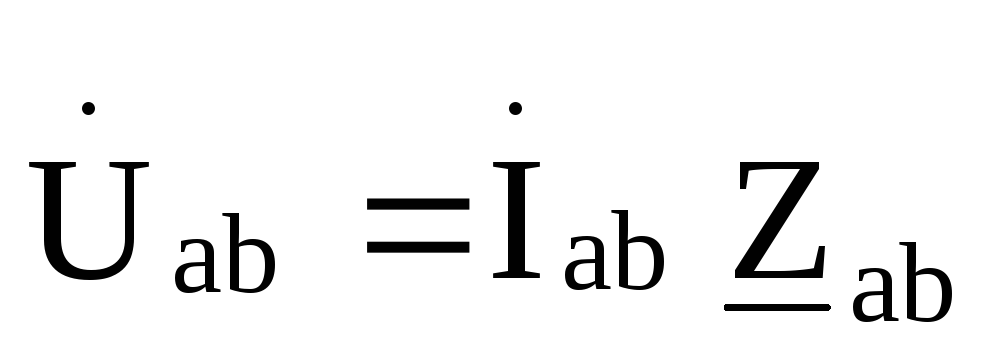 ,
,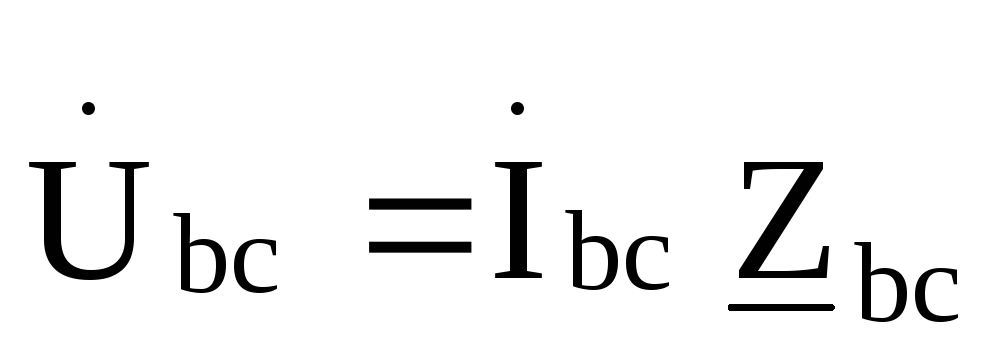 ,
,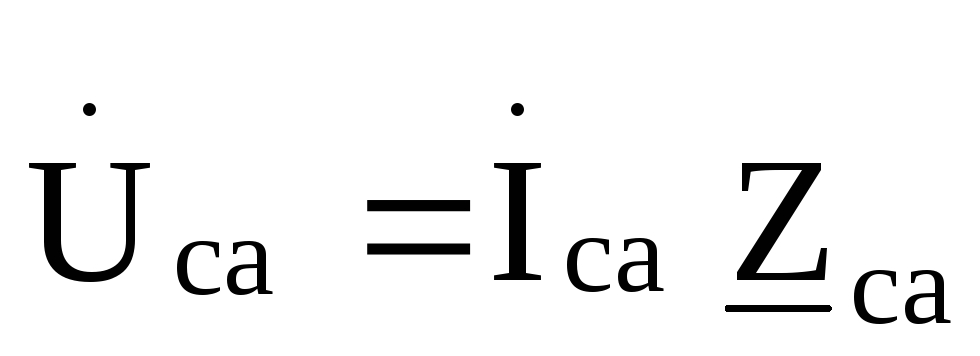 ,
,
Пример 9.8.Для цепи рис. 9.37определить токи и напряження. Построить векторно-
топографическую диаграмму
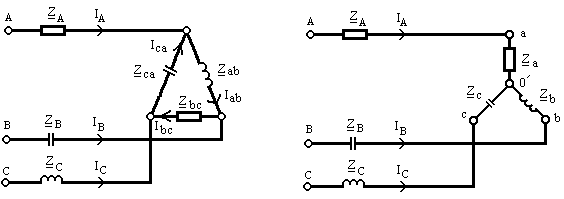
Рис. 9.37 Рис. 9.38
Линейное напряжение 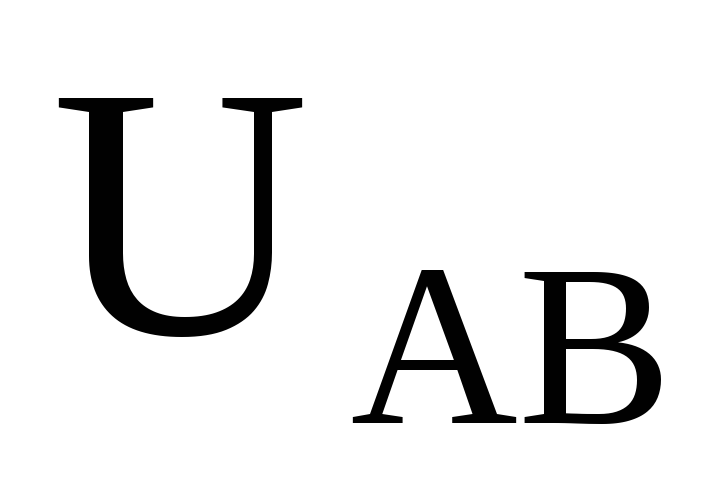 =220
В,
=220
В,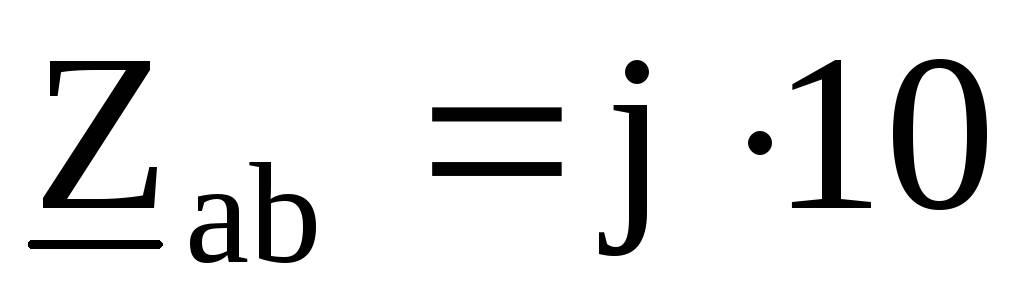 Ом,
Ом,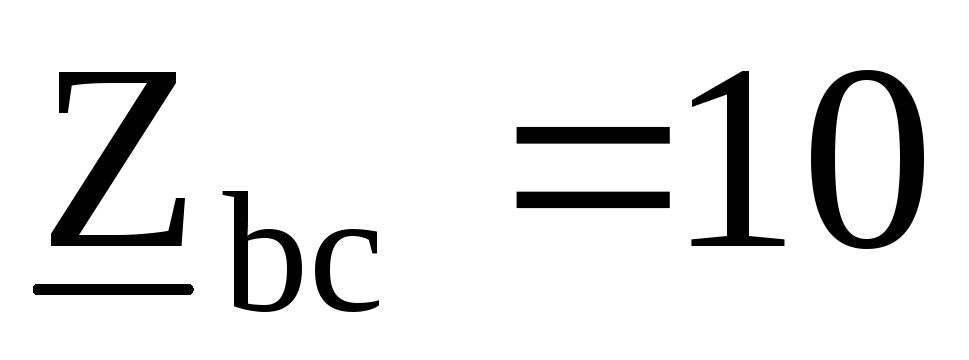 Ом ,
Ом ,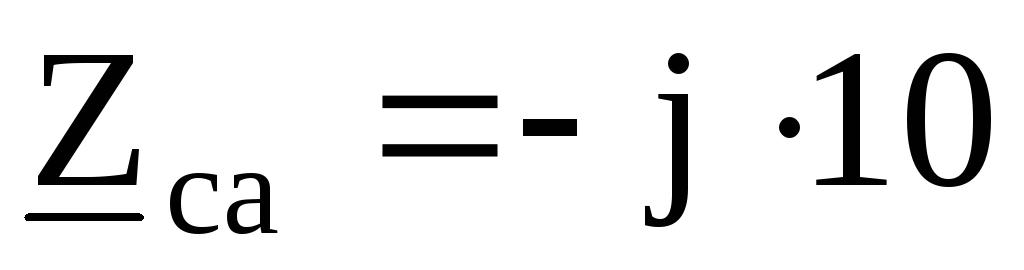 Ом,
Ом,
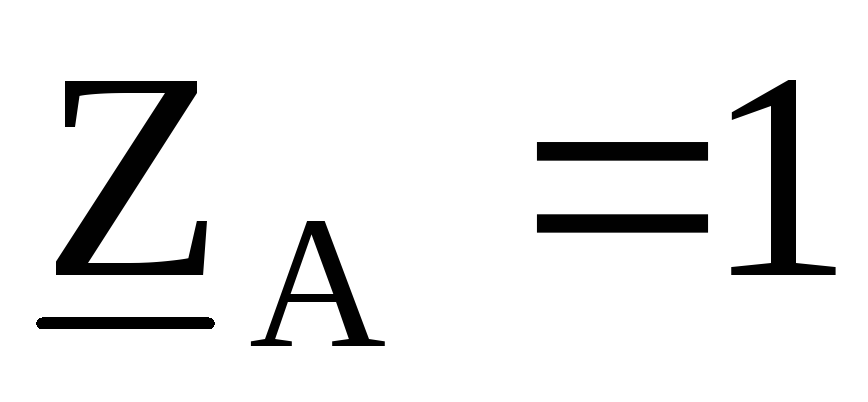 Ом,
Ом,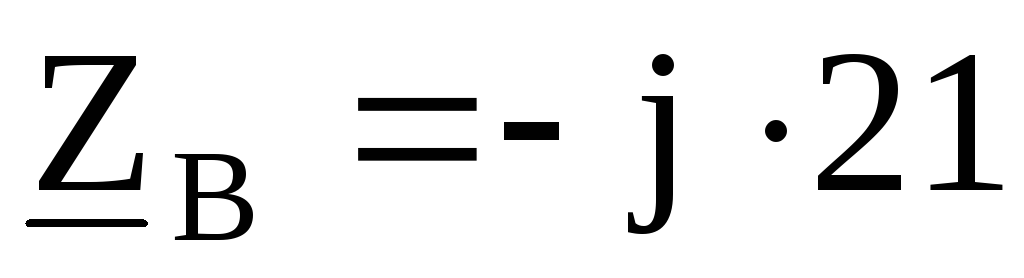 Ом,
Ом,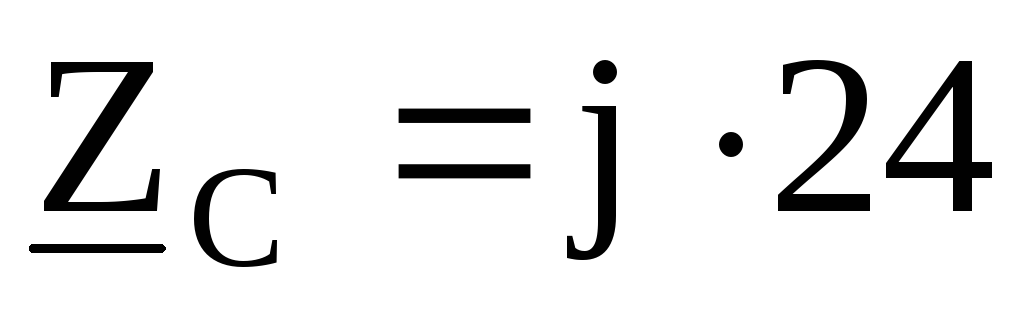 Ом
.
Ом
.
Решение
Преобразуем треугольник сопротивлений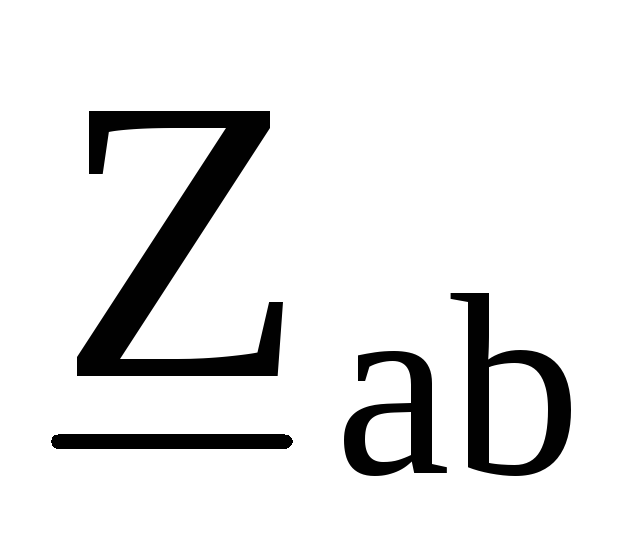 ,
,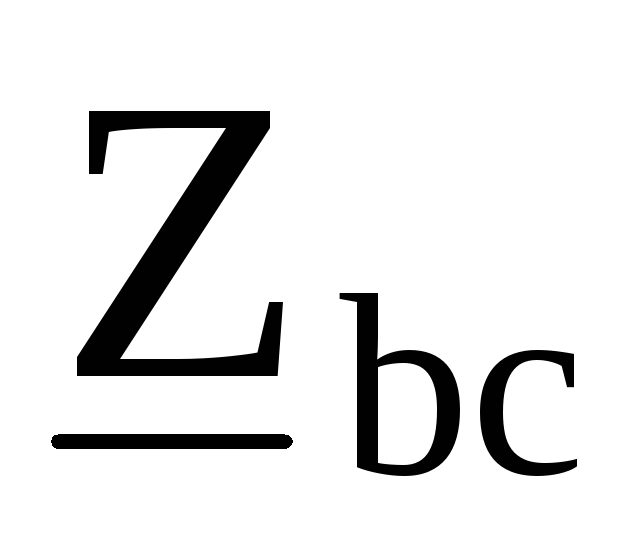 ,
,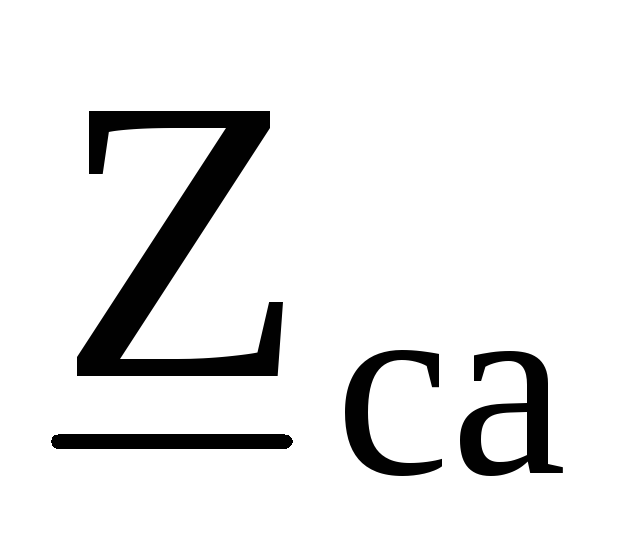 в эквивалентную звезду с
сопротивлениями
в эквивалентную звезду с
сопротивлениями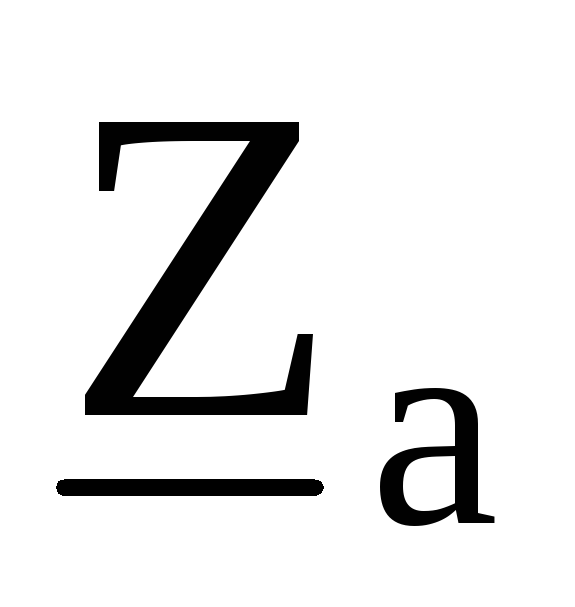 ,
,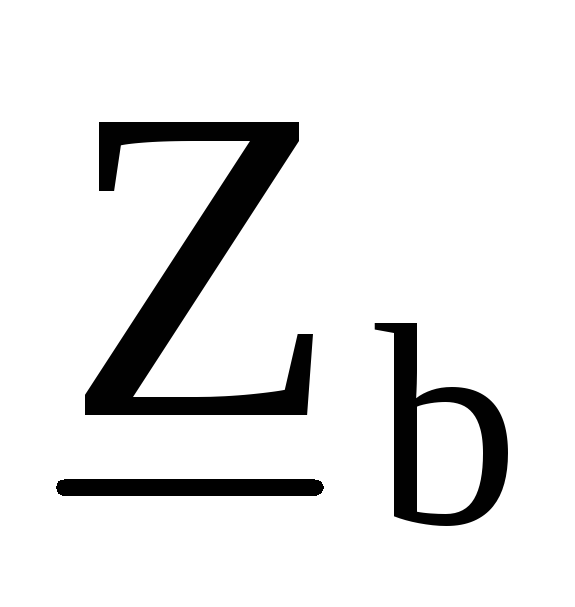 ,
,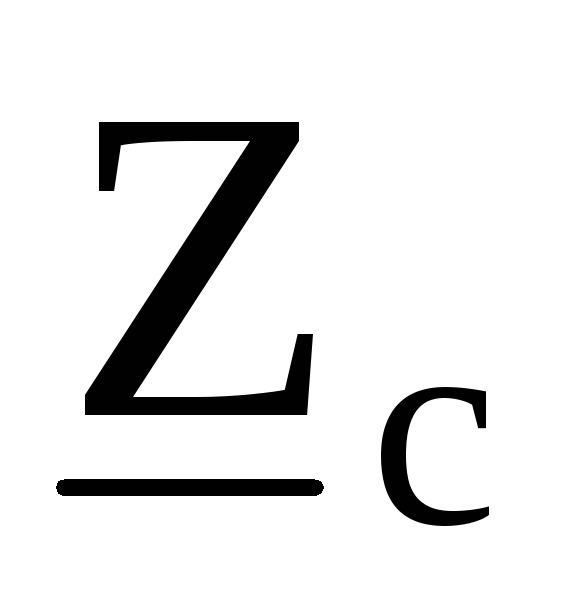 :
:
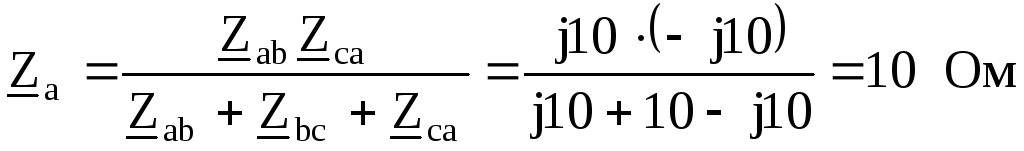
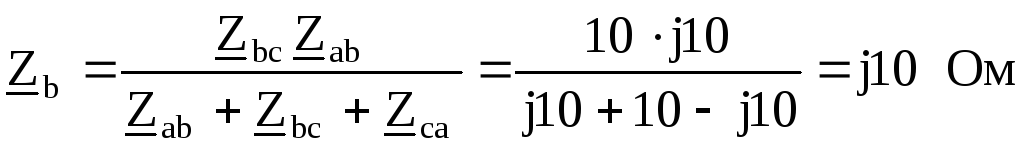
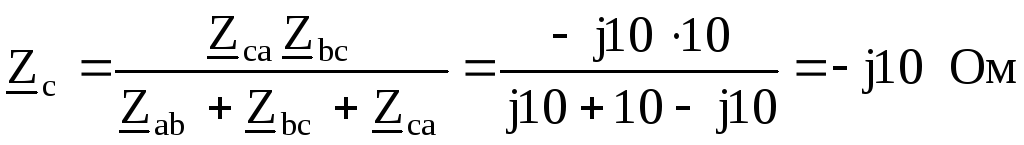
Полученные сопротивления оказываются соединенными последовательно с
соответствующимисопротивлениями в
линии 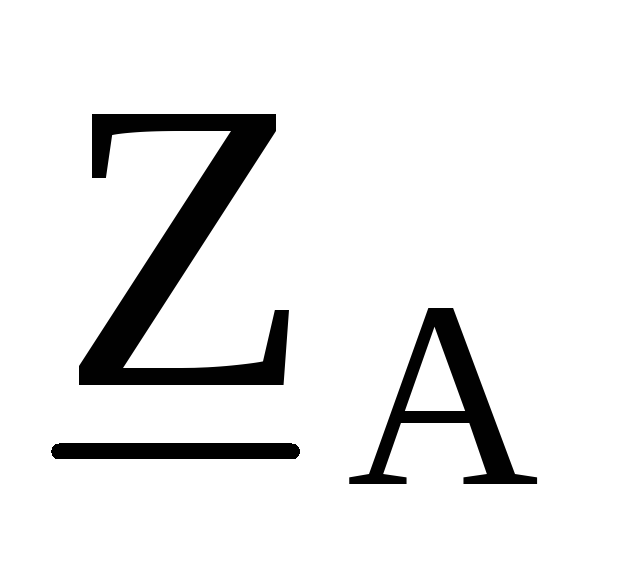 ,
,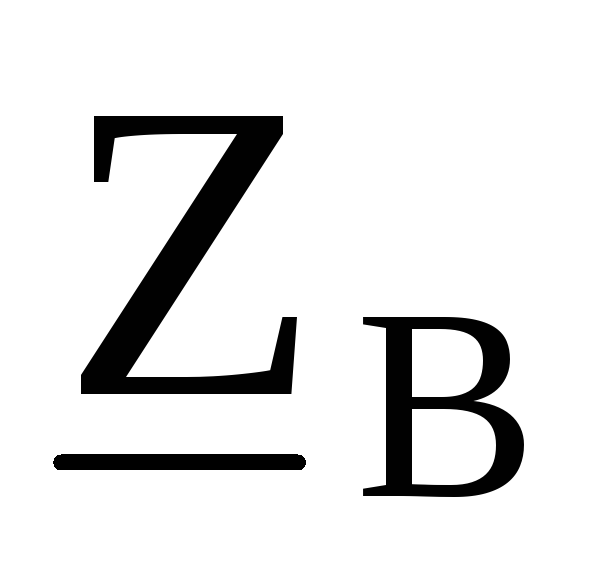 ,
,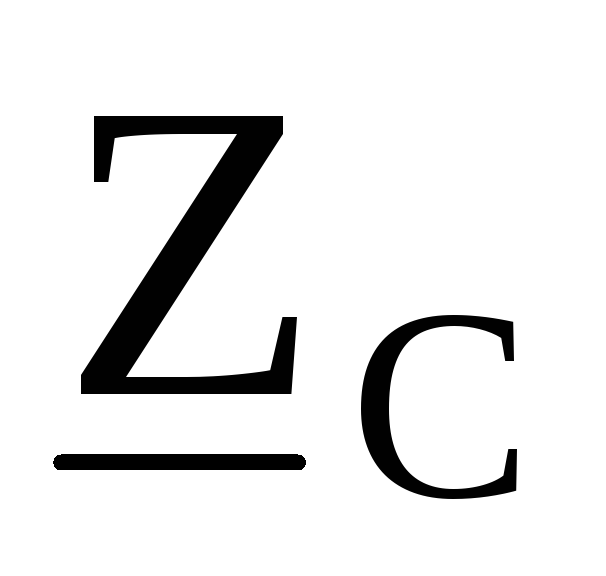 ,
как это показано на рис. 9.38.
,
как это показано на рис. 9.38.
Объединяя сопротивления в фазах, получим эквивалентную несимметричную звезду с
сопротивлениями 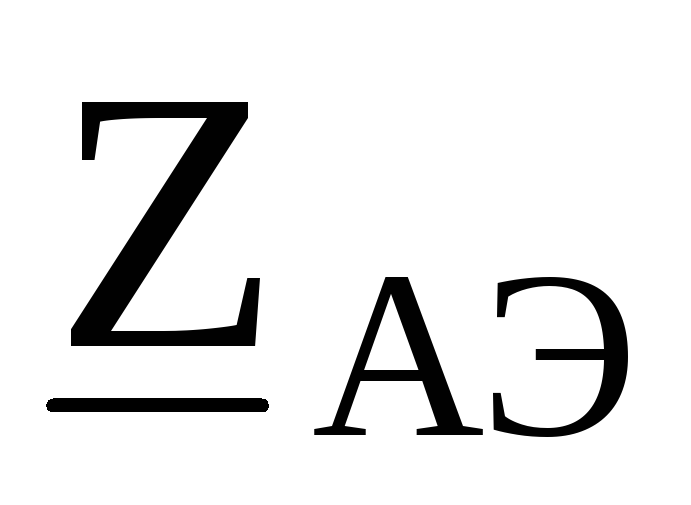 ,
,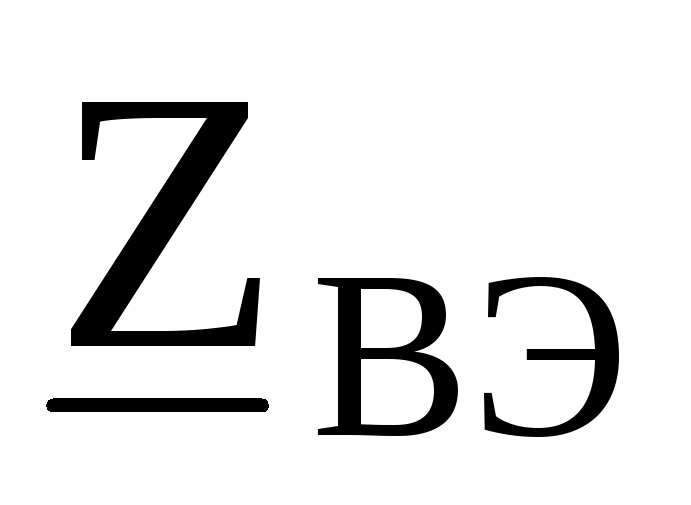 ,
,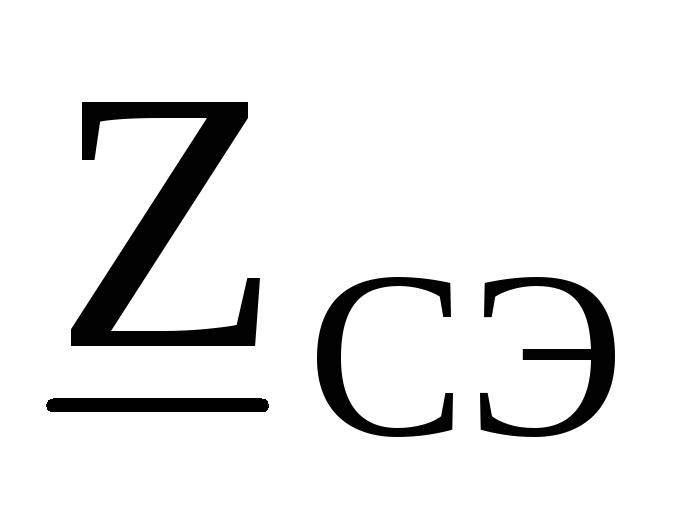 :
:
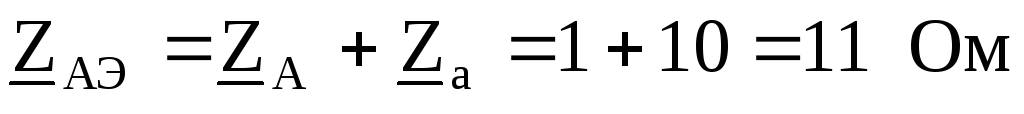
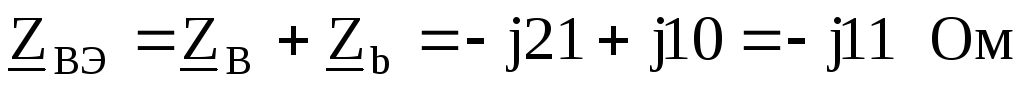
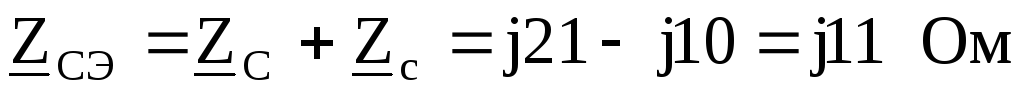
По заданному линейному напряжению найдем фазное напряжение генератора, обмотки которого соединены звездой.
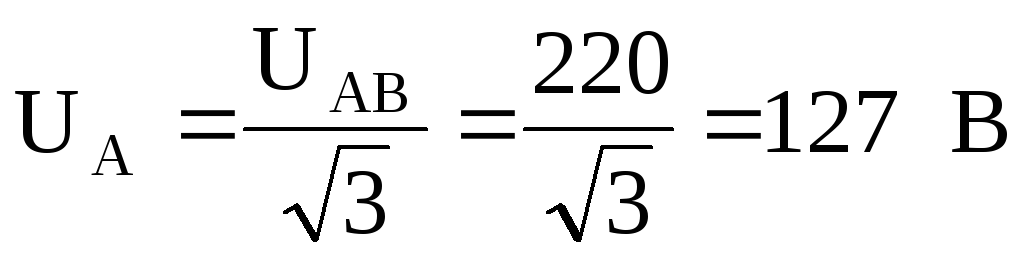
Принимаем  ,
тогда смещение нейтрали
,
тогда смещение нейтрали
позволяет найти фазные напряжения
эквивалентной звезды с сопротивлениями ,
, ,
, :
:
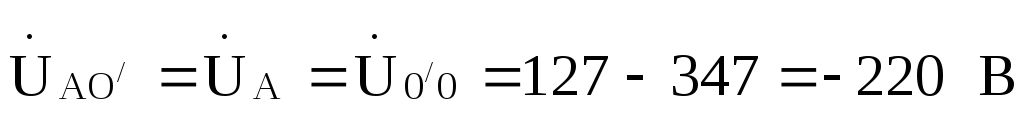
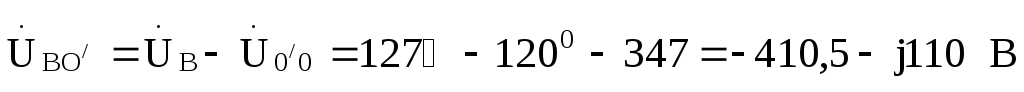
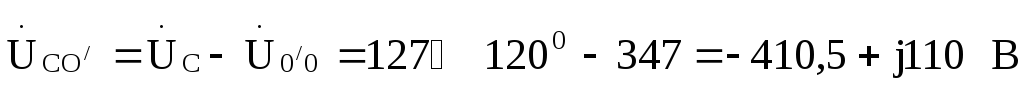
По этим напряжениям находим токи  :
:
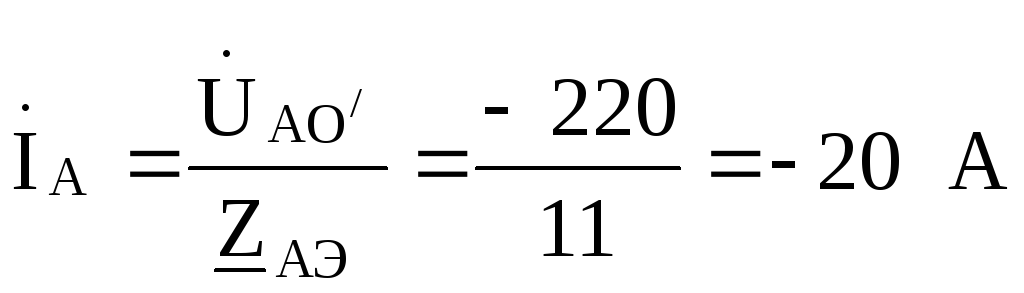
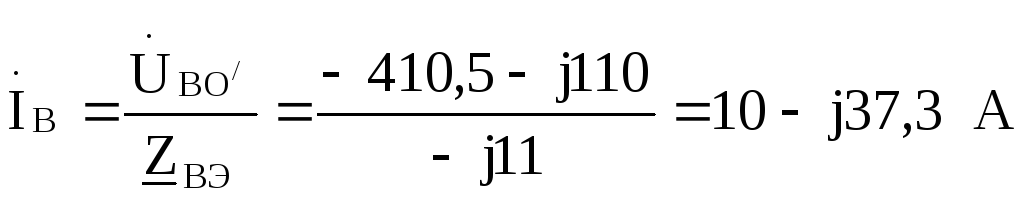
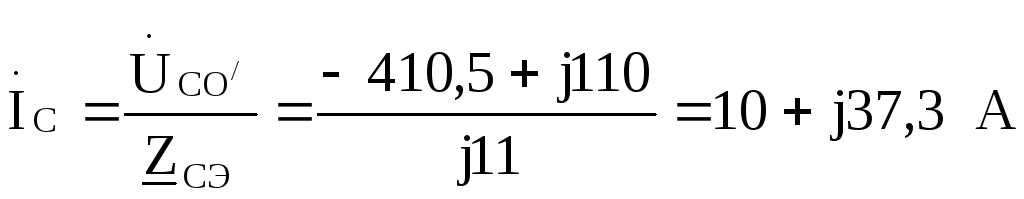
Проверка:  =
=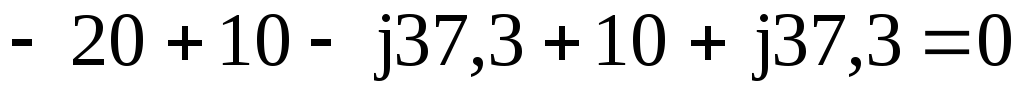 .
Теперь можно найти потенциалы точека, в, сно
отношению к потенциалу точки
.
Теперь можно найти потенциалы точека, в, сно
отношению к потенциалу точки и напряжения на зажимах треугольника
и напряжения на зажимах треугольника
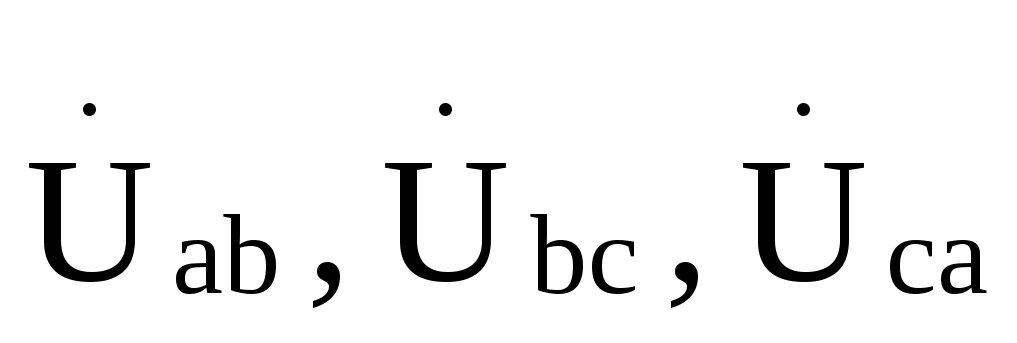 :
:
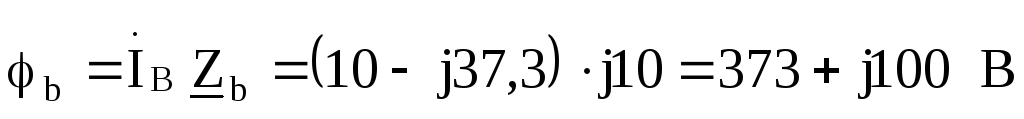
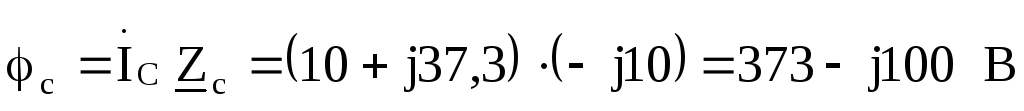

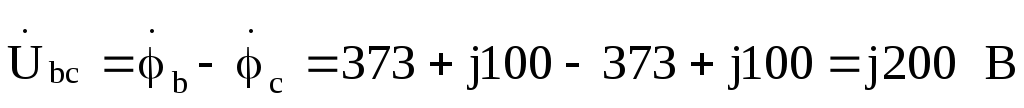
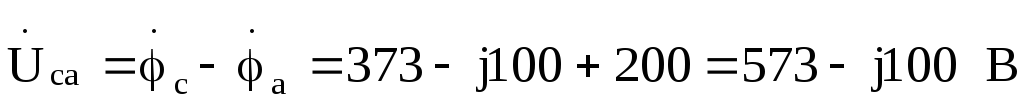
Токи в фазах треугольника:
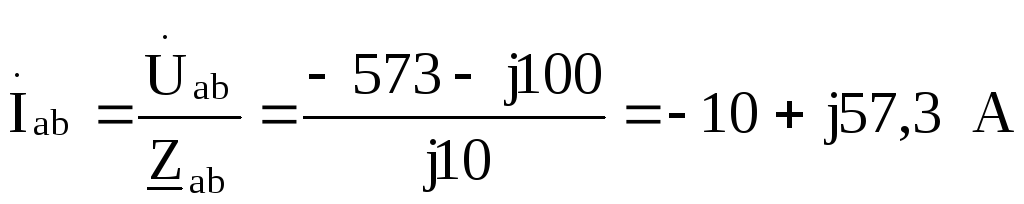 ;
;
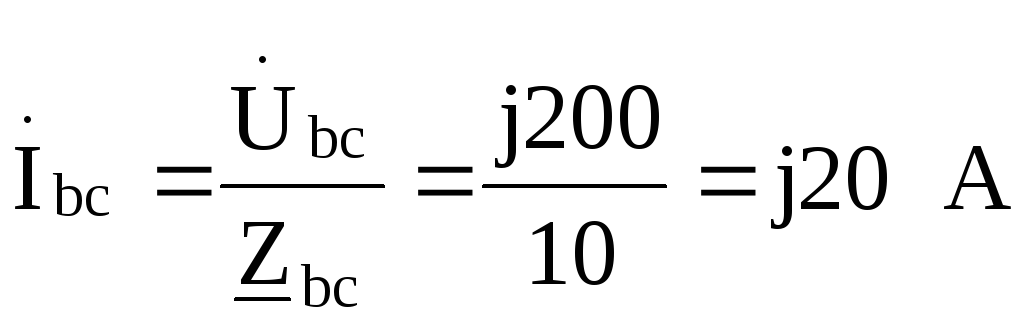 ;
;
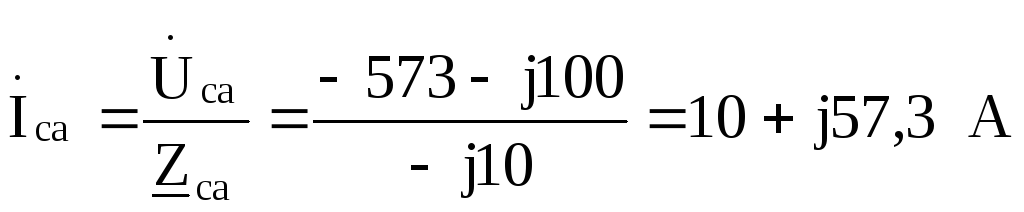 .
.
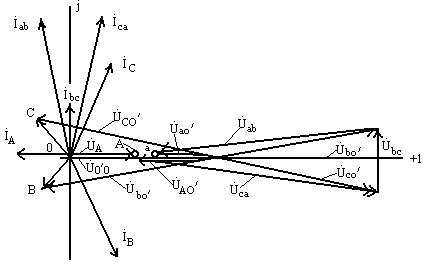
Рис. 9.39
Векторно-топографическая диаграмма приведена на рис. 9.39.
9.3. Расчет трехфазных цепей с симметричной нагрузкой
Исходными данными являются:
— схема трехфазной цепи,
— фазные ЭДС генератора,
— сопротивления фаз нагрузки.
Искомыми величинами являются токи.
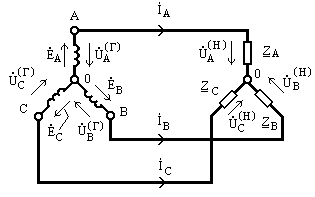
Рис. 9.9
Обмотки генератора и сопротивления нагрузки соединены в звездy, как показано нaрис. 9.9
(без нулевого провода).
По условию: 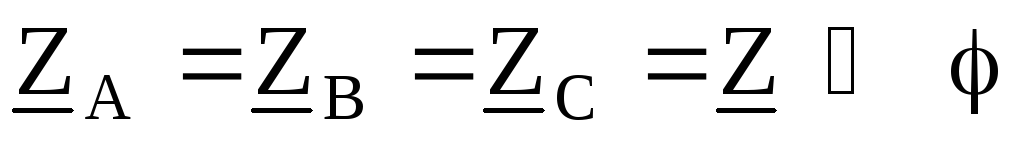
Заданные фазные ЭДС генератора в комплексной форме можно записать так
если 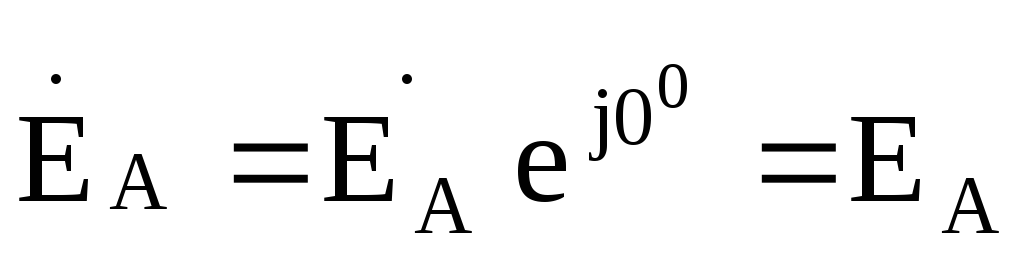 ,
то
,
то
 ,
,
Напряжение между нейтральными точками нагрузки и генератора находим по методу двух узлов
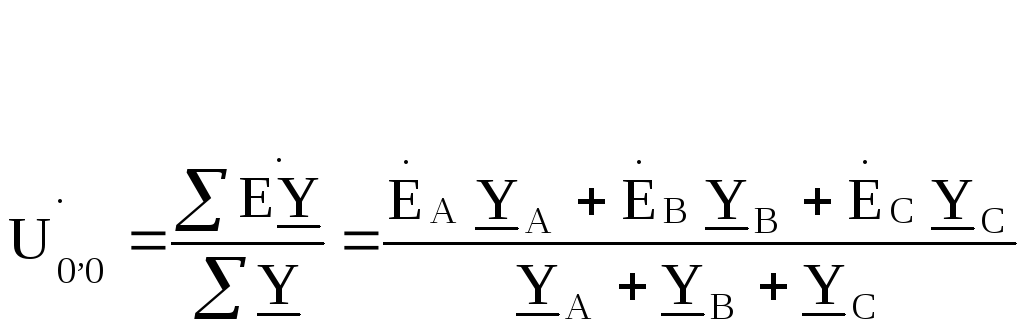
Так как для симметричной нагрузки 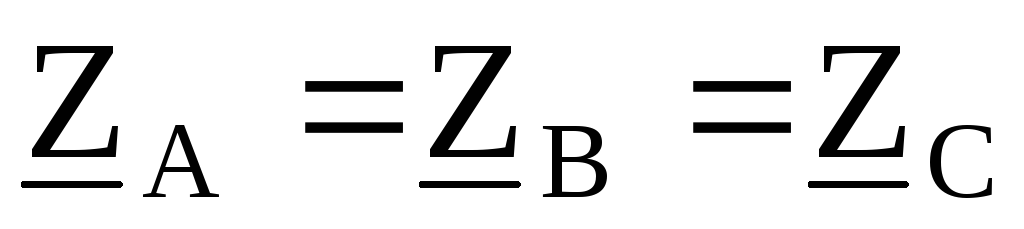 и
и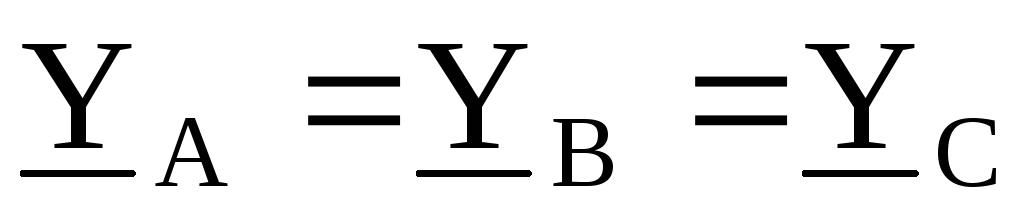 ,
то, учитывая
,
то, учитывая
соотношение (9.2),найдем
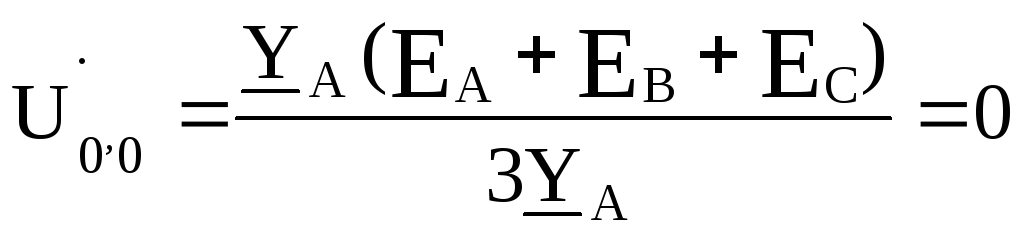
Вывод , который необходимо запомнить: у симметричной нагрузки, соединенной звездой,
потенциал нейтральной точки 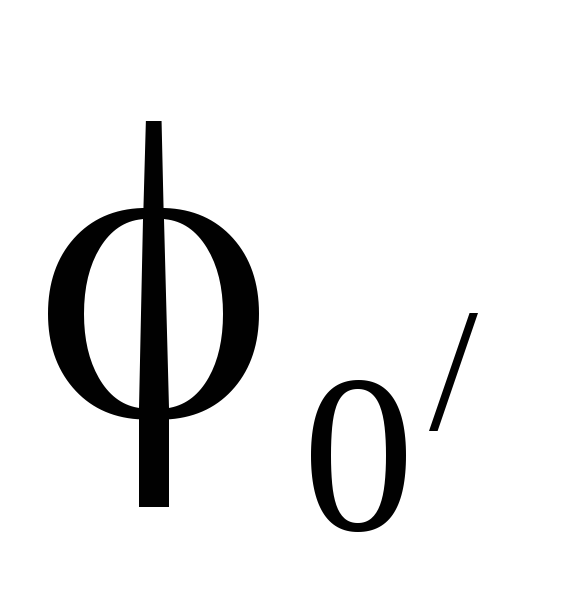 равен потенциалу нейтральной точки
генератора
равен потенциалу нейтральной точки
генератора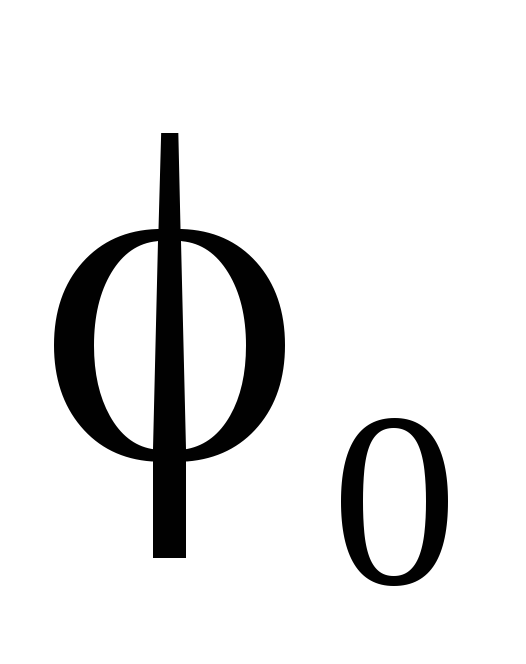 .
Отсюда
.
Отсюда
следует, что эти точки можно соединить между собой проводником и тогда становится ясным,
что 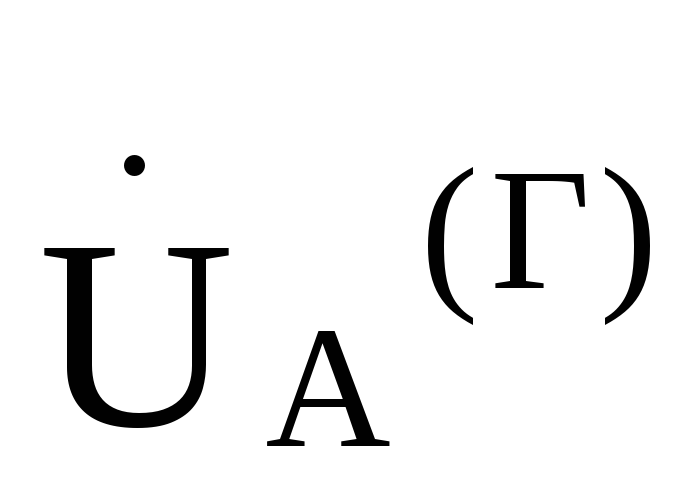 =
=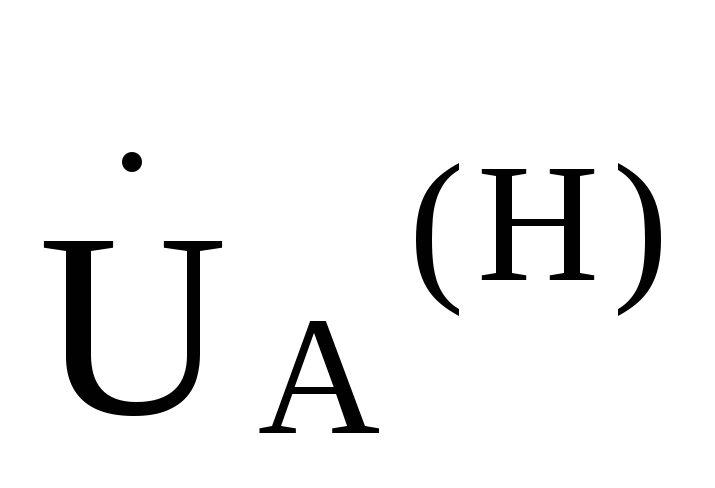 ,
,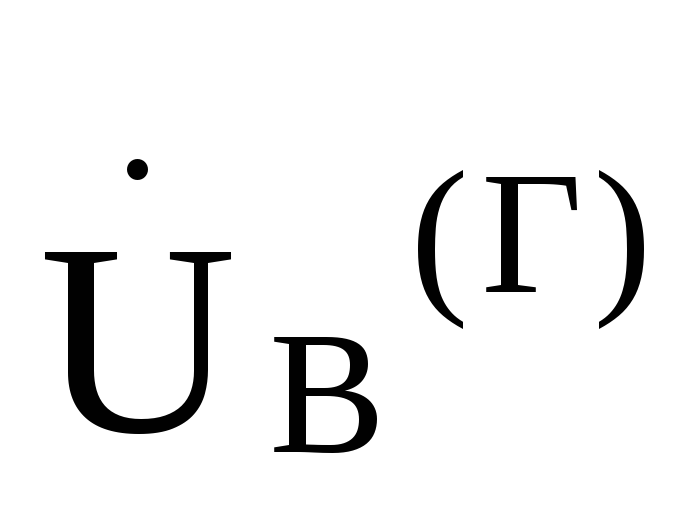 =
=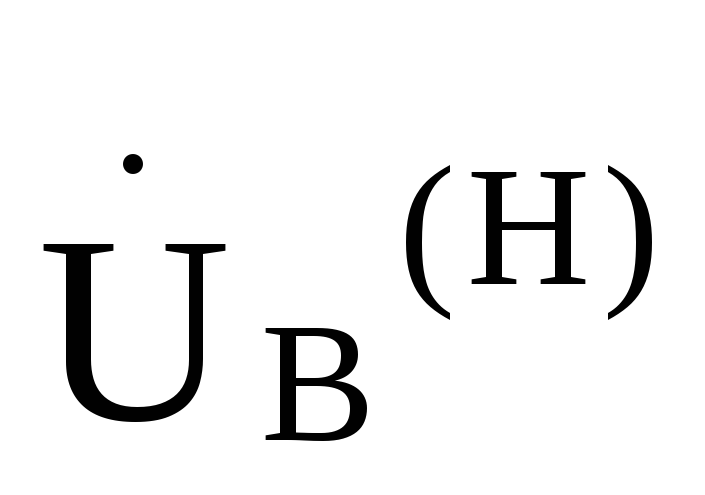 ,
,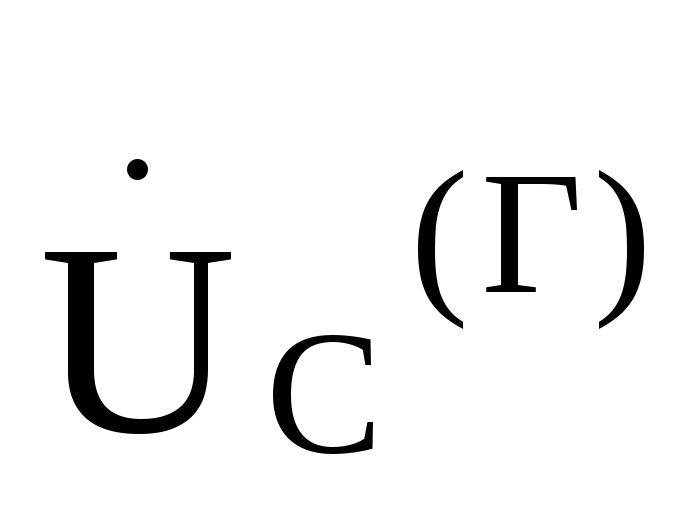 =
=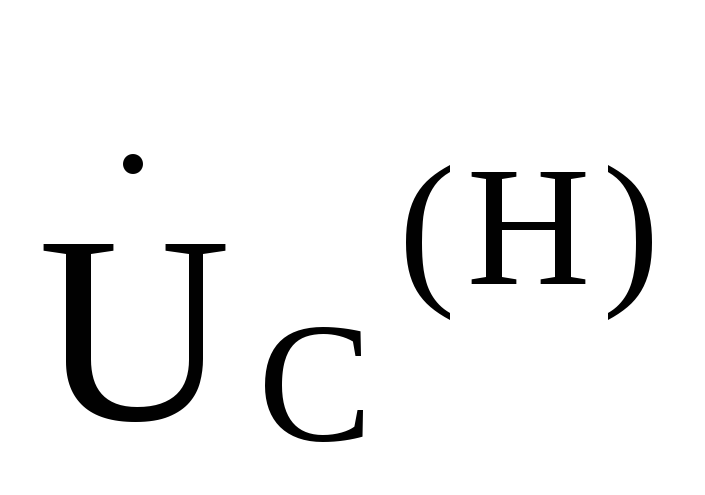 и токи в фазах нагрузки будут
и токи в фазах нагрузки будут
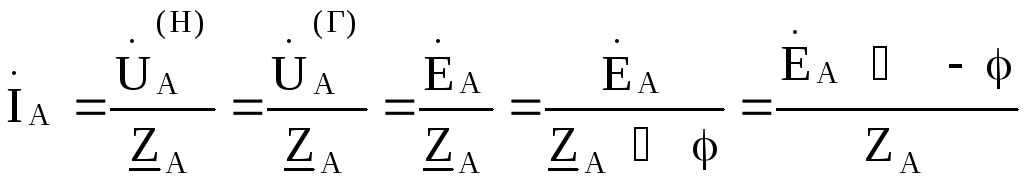

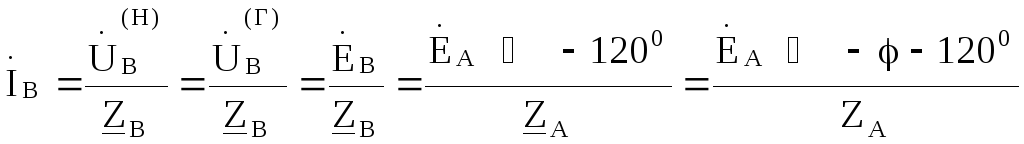
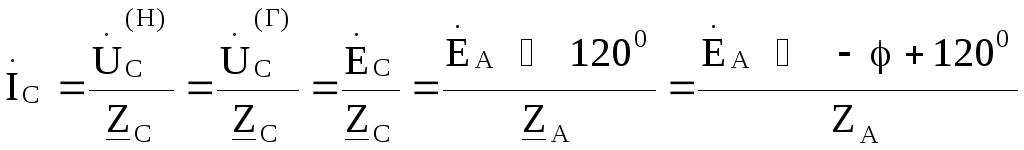
Из схемы очевидно, что фазный ток нагрузки является линейным током и он же есть ток в фазе
генератора.
Покажем, что напряжение между любыми двумя линейными проводами, называемое —
линейным напряжением, в 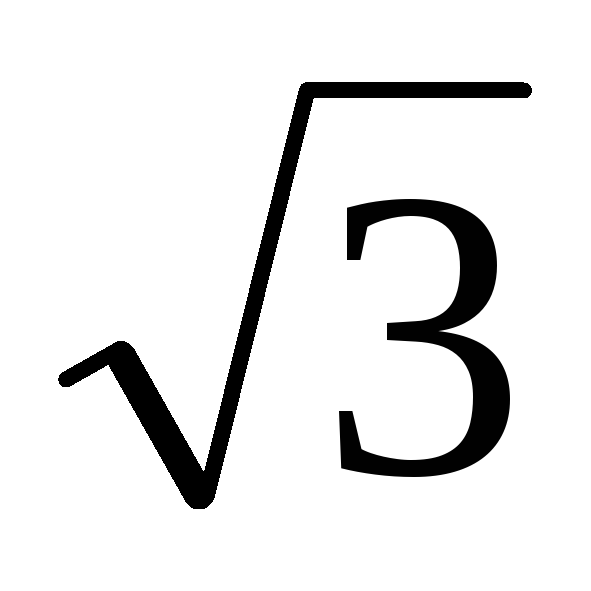 раз
больше фазного напряжения, т. е.
раз
больше фазного напряжения, т. е.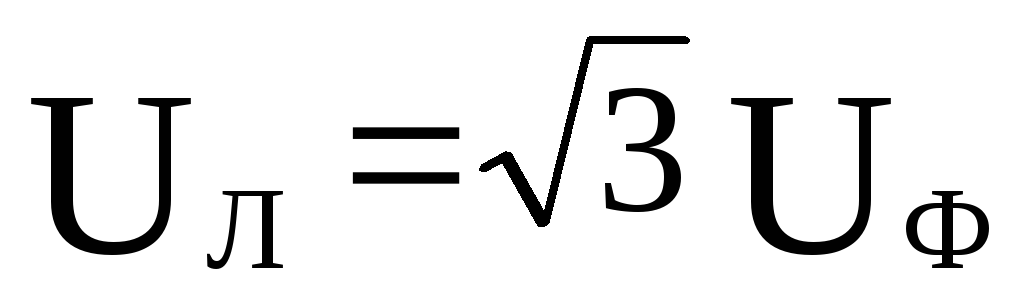 .
.
Для этого найдем, например, разность комплексных потенциалов точек А и В
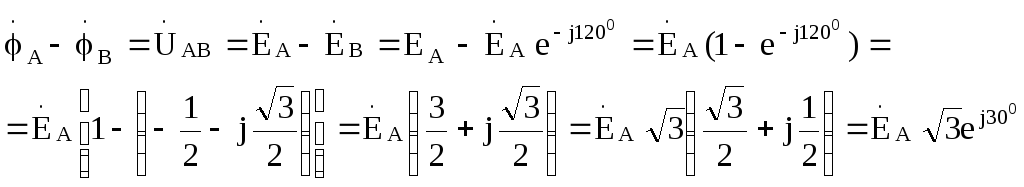
Таким
образом, линейное напряжение 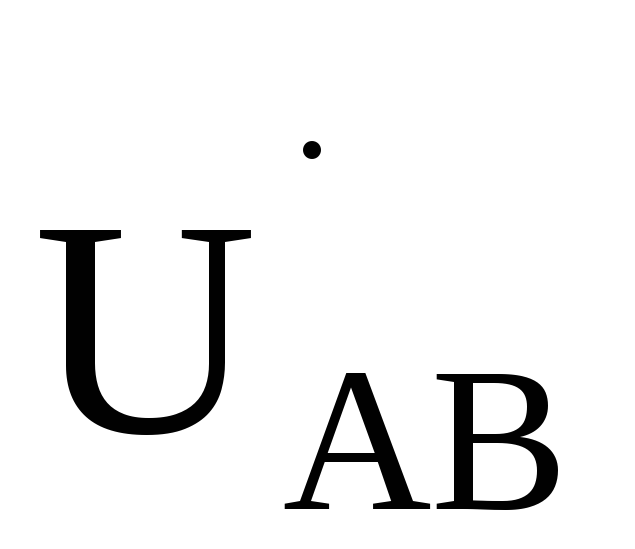 в
в 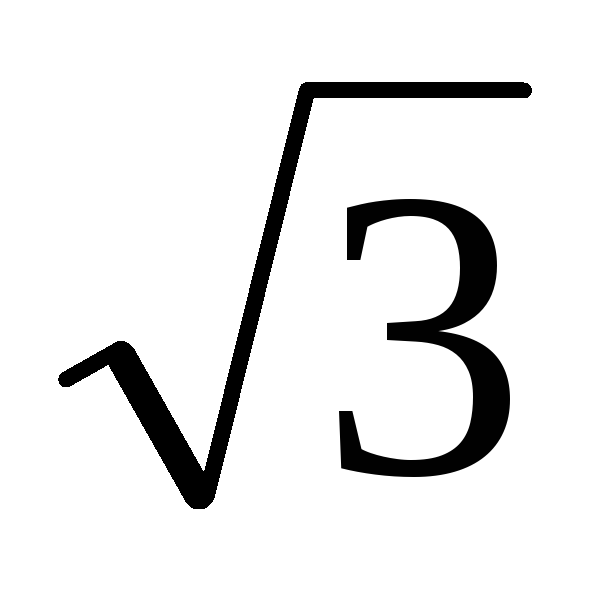 раз
больше фазного
раз
больше фазного 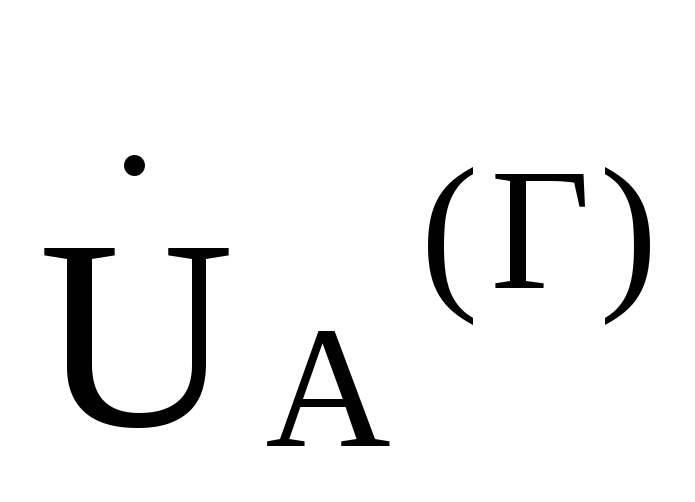 и
на
30°
и
на
30°
опережает его. Аналогично можно
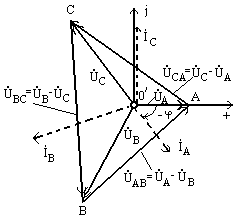
Рис. 9.10
получить, что линейное напряжение 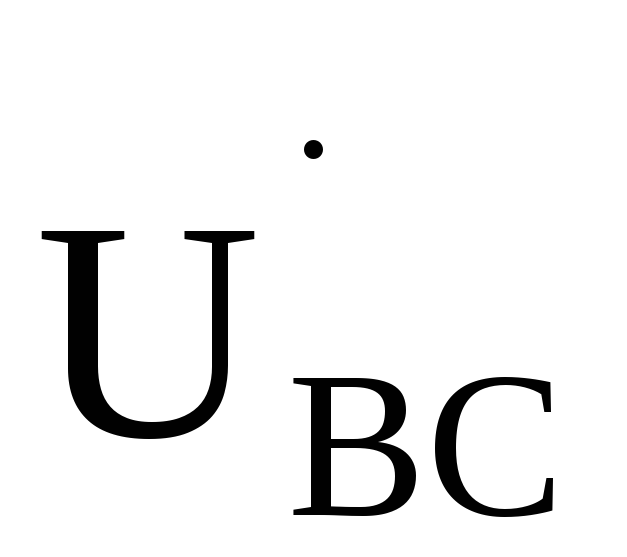 опережает фазное напряжение
опережает фазное напряжение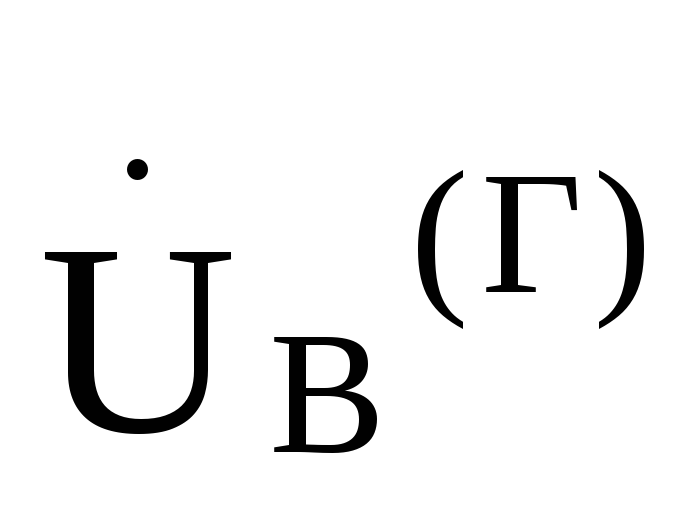 на
30°и в
на
30°и в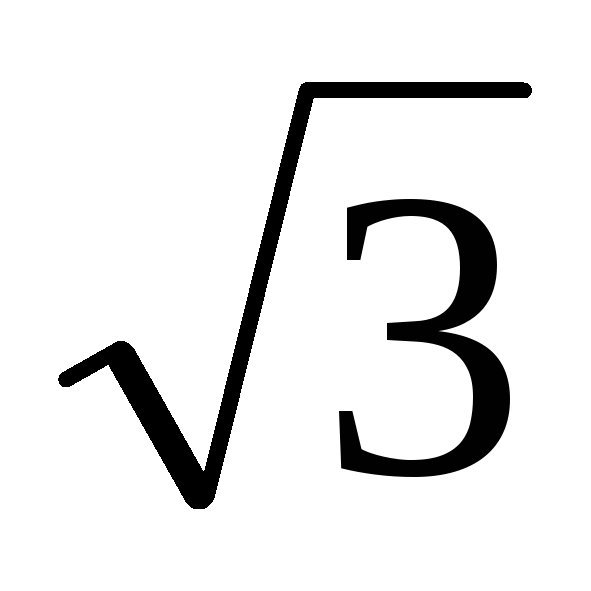 раз
больше его и линейное напряжение
раз
больше его и линейное напряжение опережает фазное напряжение
опережает фазное напряжение  на 30°
на 30°
uв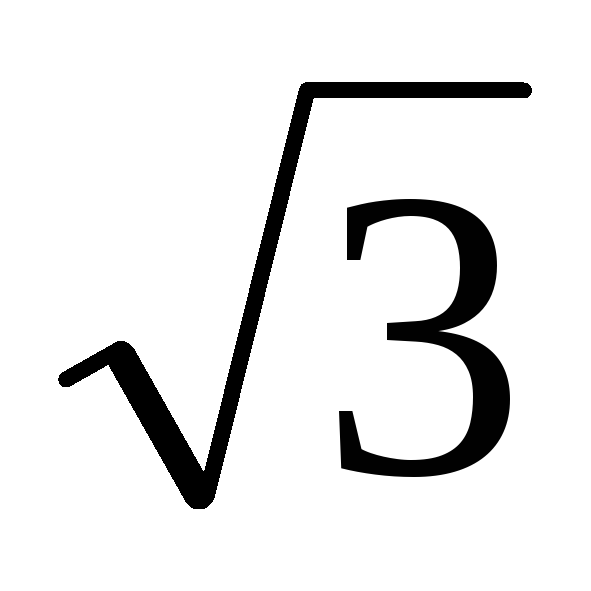 раз
больше, его. Приведенные соотношения
проще всего запомнить с помощью построения
топографической диаграммы для фазных
и линейных напряжений, приведенной
на рис. 9.10.Векторы фазных
напряжений
раз
больше, его. Приведенные соотношения
проще всего запомнить с помощью построения
топографической диаграммы для фазных
и линейных напряжений, приведенной
на рис. 9.10.Векторы фазных
напряжений ,
, ,
и
,
и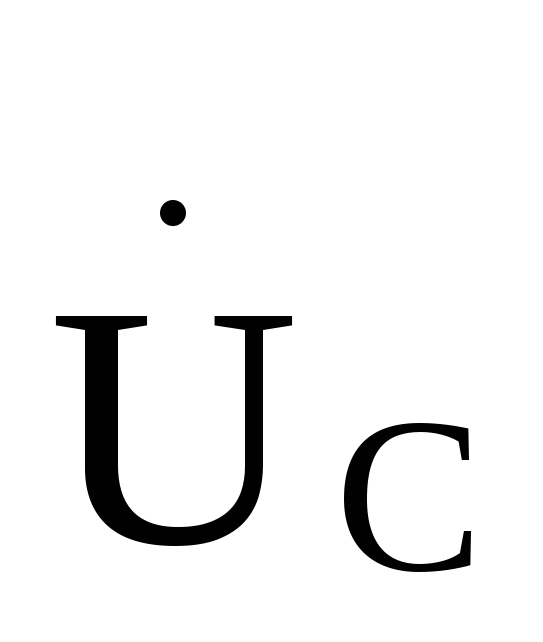 этой диаграммы относятся ках к фазным
напряжениям генератора, так и к фазным
напряжениям нагрузки, т. е. топографические
диаграммы фазных напряжений генератора
и нагрузки совпадают. Векторная диаграмма
токов для схемы рис. 9.9показана на рис. 9.10пунктирными линиями.
этой диаграммы относятся ках к фазным
напряжениям генератора, так и к фазным
напряжениям нагрузки, т. е. топографические
диаграммы фазных напряжений генератора
и нагрузки совпадают. Векторная диаграмма
токов для схемы рис. 9.9показана на рис. 9.10пунктирными линиями.
Следует отметить, что расчет токов и напряжений на отдельных участках трехфазной цепи с симметричной нагрузкой можно и нужно проводить на одну фазу, например, на фазу А, тогда соответствующие величины в фазе Вбудут отличаться только аргументом (углом) величиной
-120°,а в фазеС.– аргументом величиной +120°.
Пример 9.1.В цепи
рис. 9.11. рассчитать токи и построить
векторно-топографическую диаграмму
приr=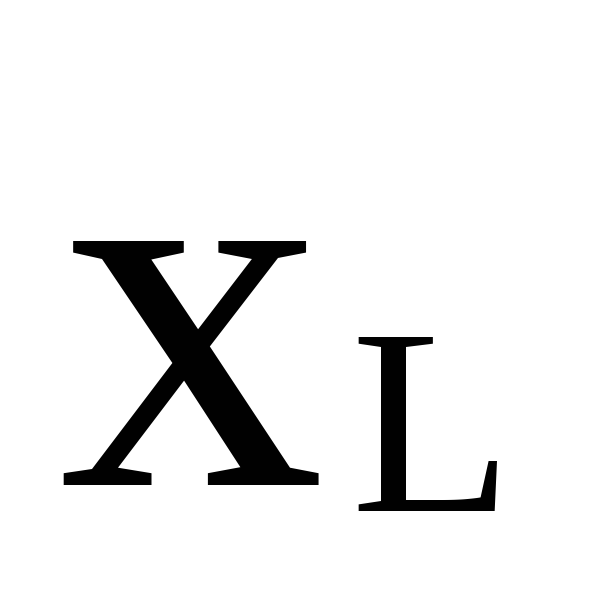 =10
Ом и фазном напряжении генератора
=10
Ом и фазном напряжении генератора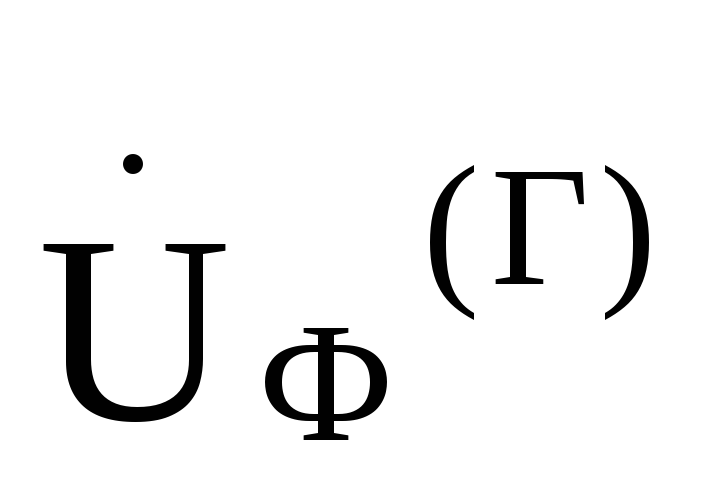 =220В.
=220В.
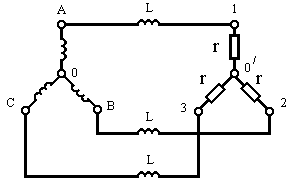
Рис. 9.11
Решение
Так как точки 0и
0’имеют одинаковые потенциалы, то
для фазы А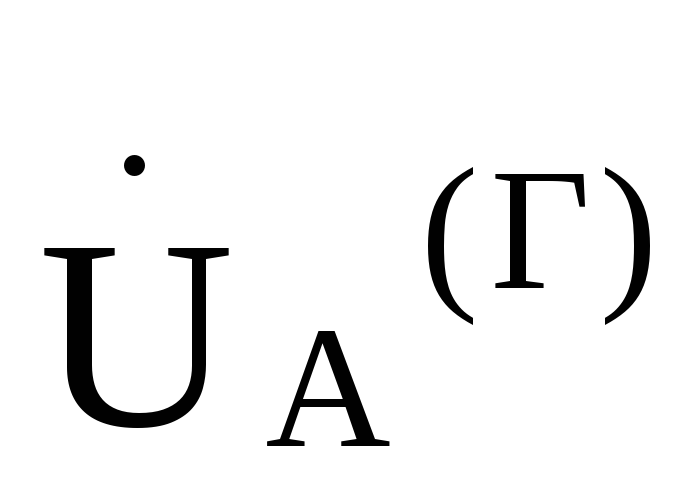 =
=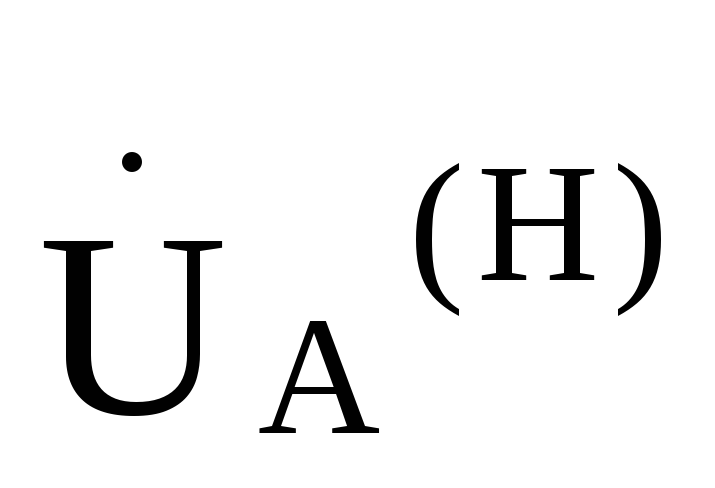 .
.
Принимаем
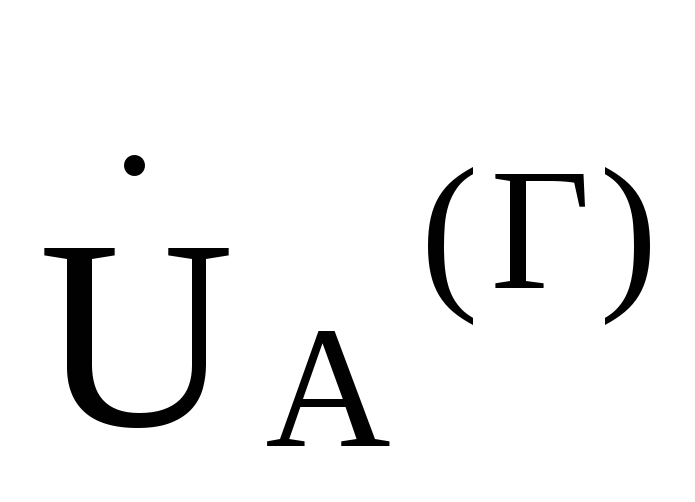 ==220
==220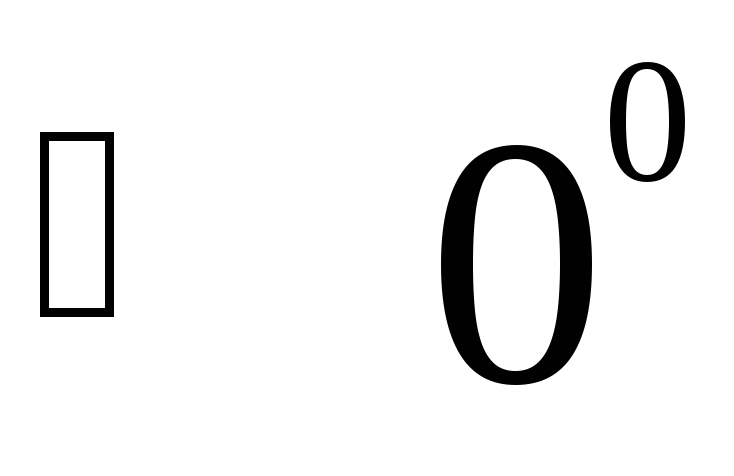 В,
тогда
В,
тогда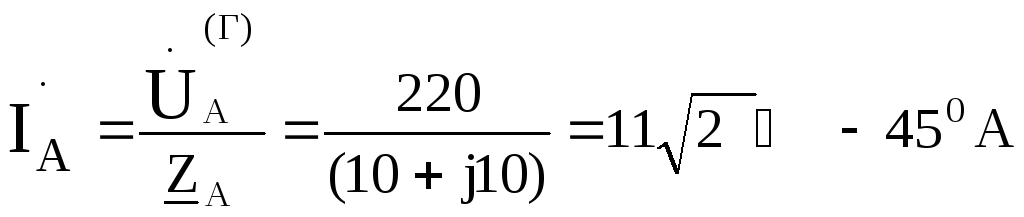 .
.
Токи в фазах ВиСотличаются
от тока только своими аргументами, т.е.
только своими аргументами, т.е.
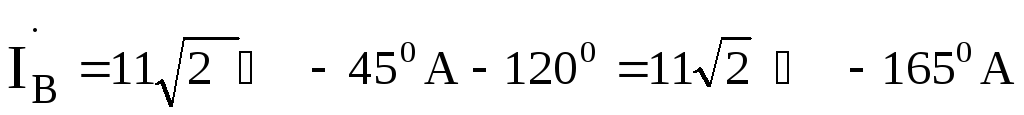
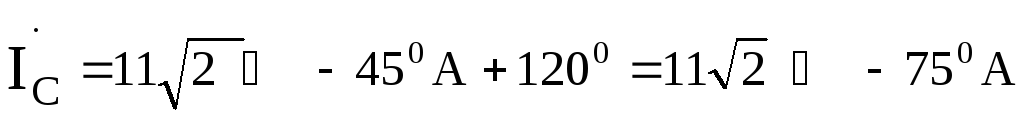
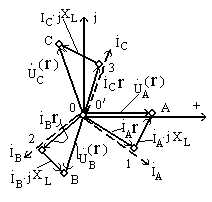
Рис. 9.12
Построение векторно-топографической
диаграммы проведем в следующей
последовательности. Отложим по
действительной оси вектор фазного
напряжения фазы А генератора 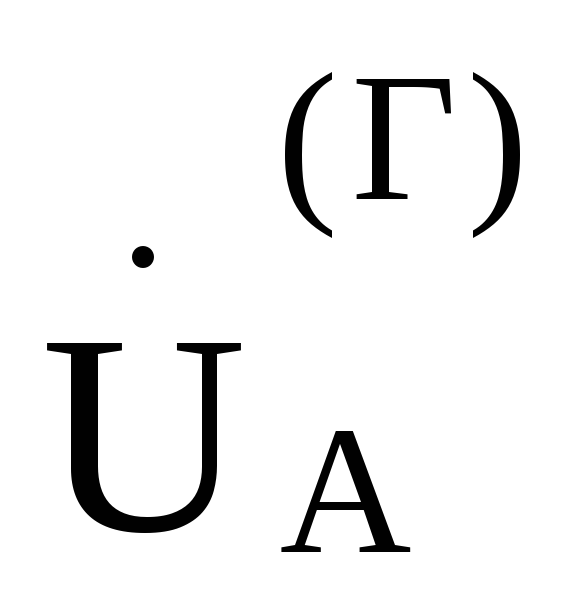 .
.
Затем в выбранном масштабе для напряжения под углами —120°и +120°по отношению к этому вектору из точки 0,потенциал которой принят равным нулю, отложим соответственно векторы
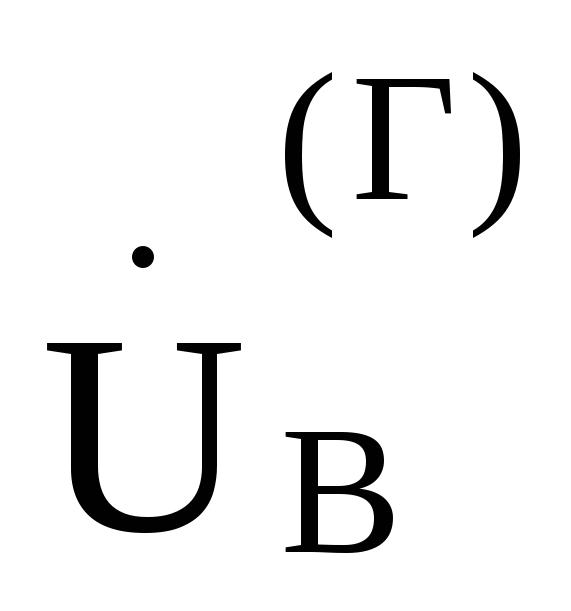 и
и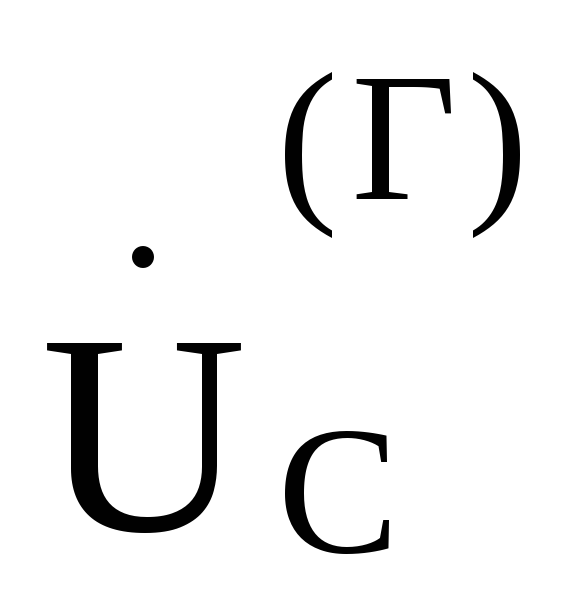 ,
как показано на рис. 9.I
2.Далее под углом —45°по
отношению к вектору
,
как показано на рис. 9.I
2.Далее под углом —45°по
отношению к вектору
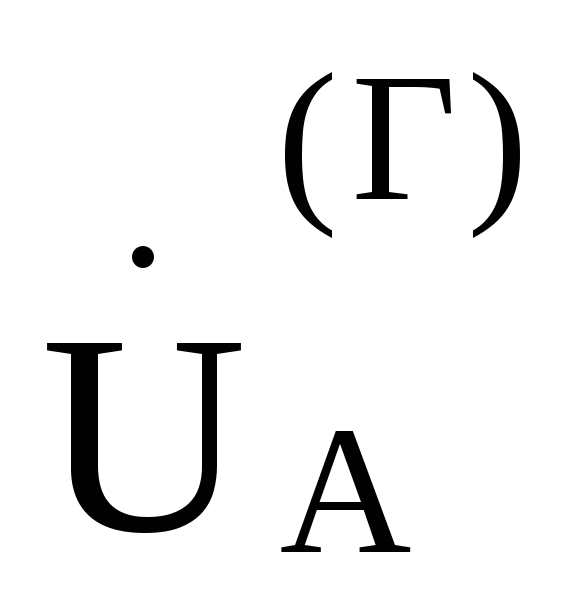 откладываем
в маштабе для тока вектор тока
откладываем
в маштабе для тока вектор тока Векторы токов
Векторы токов и
и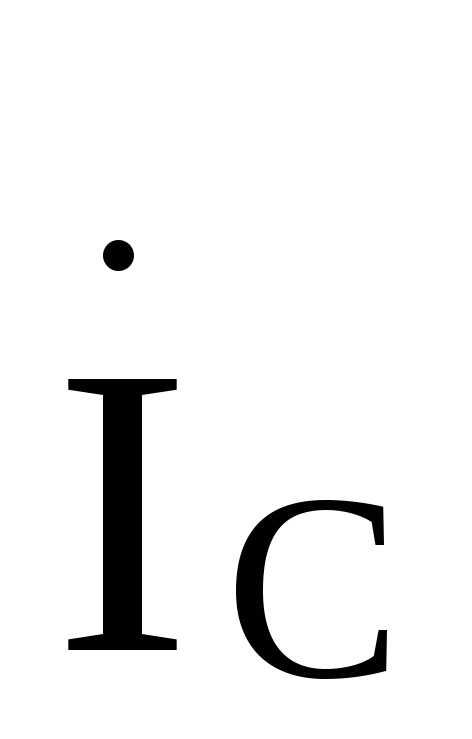 строим
строим
соответственно, под углами
—120°и+120°по отношению
к вектору тока .
Затем для каждой
.
Затем для каждой
из фаз нагрузки определяем комплексные потенциалы точек 1, 2 и 3 по отношеную к потенциалу
точки 0′,равному так-же нулю:


Найденные комплексные потенциалы откладываем от точки О’ по направлениям соответствующих токов в масштабе для напряжения.
Далее определяем потенциалы точек А, В, Спо отношению к потенциалу точки О’:
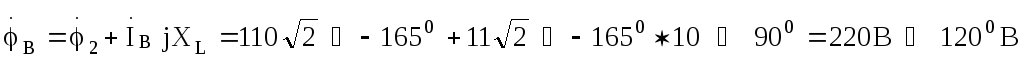
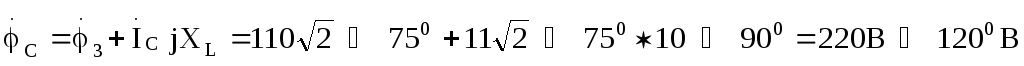
Отметим, что напряжения на индуктивностях нагрузки можно было бы найти графически,
используя соотношения:
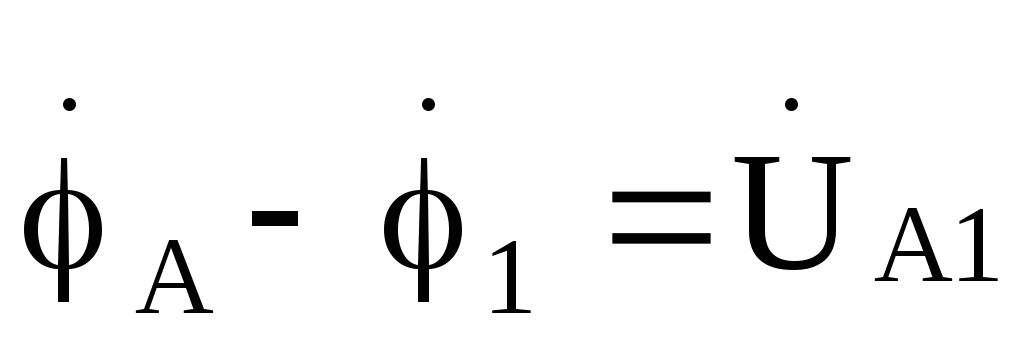 ;
;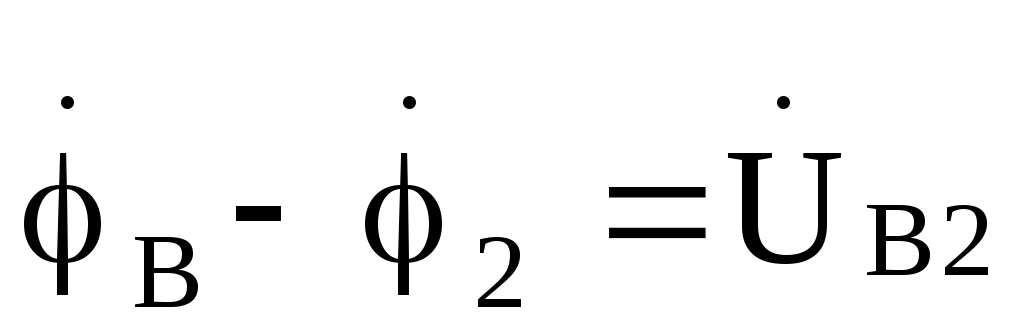 ;
;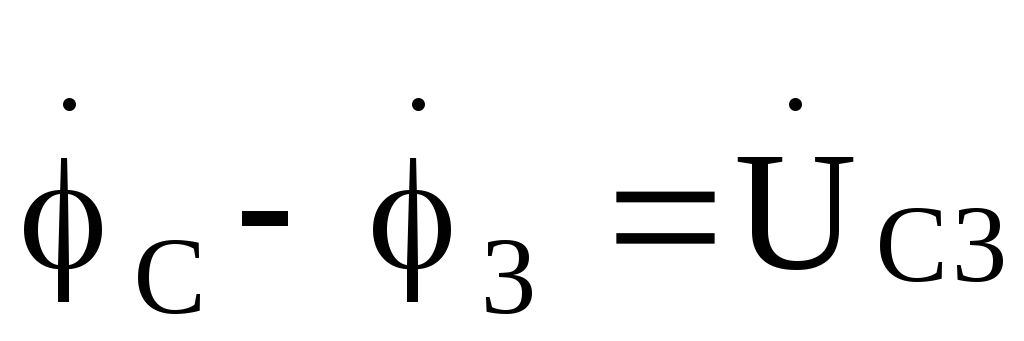
При этом для получения .напряжения  надо на диаграмме соединить точкиАи 1прямой и указать
направление этой прямой к первому
индексу, т.е. к точкеА.Аналогично
. получают напряжения
надо на диаграмме соединить точкиАи 1прямой и указать
направление этой прямой к первому
индексу, т.е. к точкеА.Аналогично
. получают напряжения ;
;
2.Обмотки генератора и сопротивления нагрузки соединены в треугольник, как показано на рис. 9.13.
Из схемы рис .9.13непосредственно следует, что фазные
напряжения генератора, именуемые теперь
как ,
,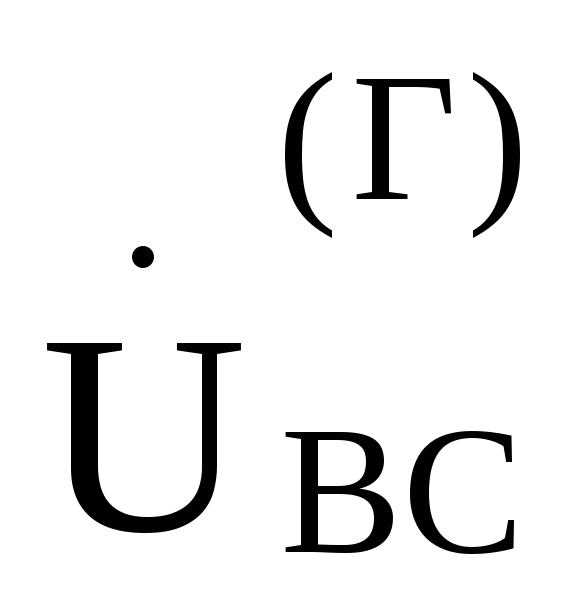 ,
,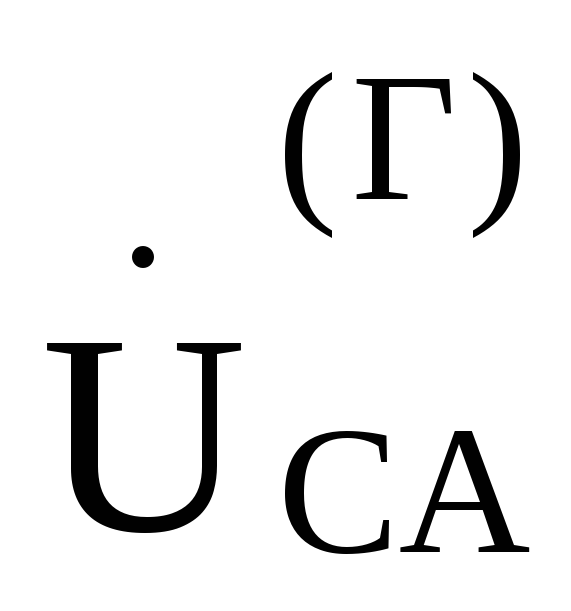 ,
,
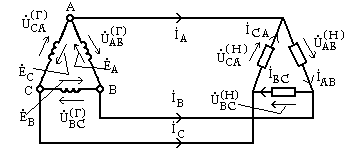
Рис. 9.13
линейные напряжения между соответствующими парами проводов и фазные напряжения
нагрузки 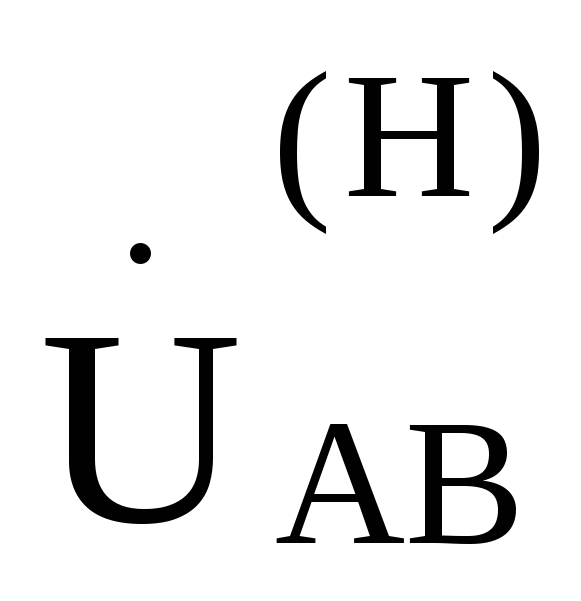 ,
,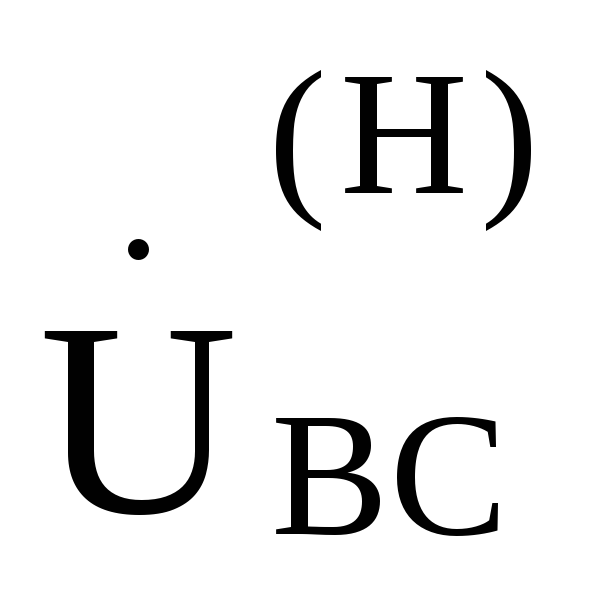 ,
,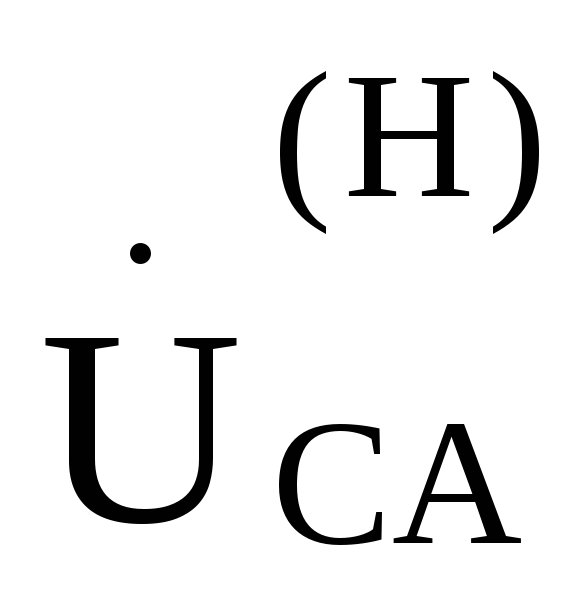 ,—соответственно равны друг другу.
Другими словами, при
,—соответственно равны друг другу.
Другими словами, при
соединений треугольником линейные напряжения равны соответствующим фазным
напряжениям. Поэтому фазные токи нагрузки определяются через заданные фазные ЭДС и
сопротивления нагрузки по соотношениям:
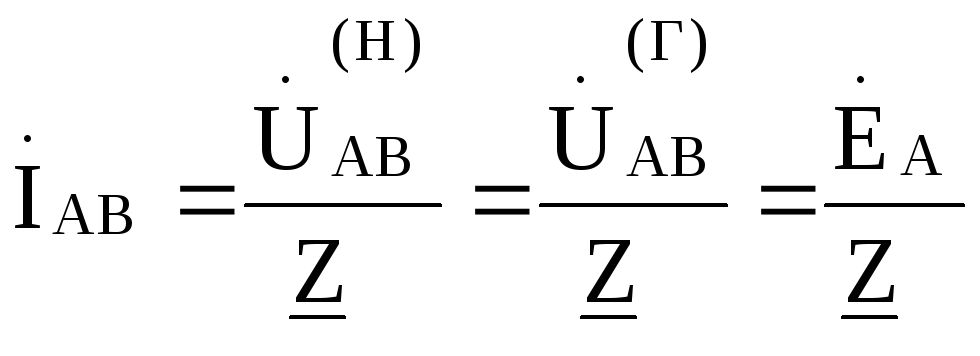

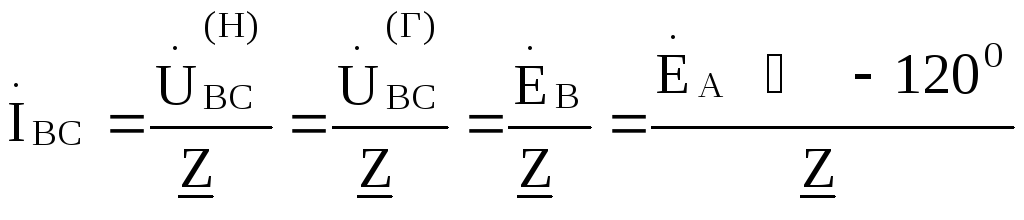
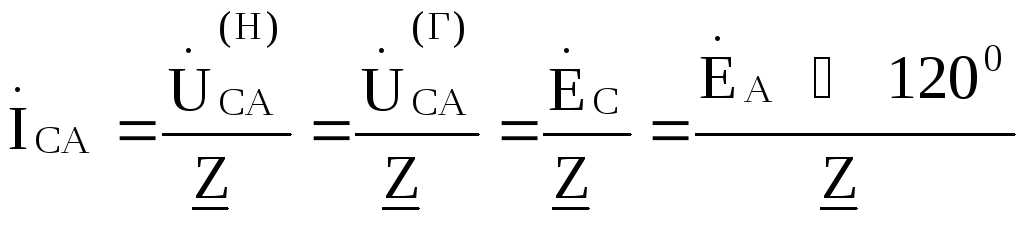
Линейные токи  ,
, ,
,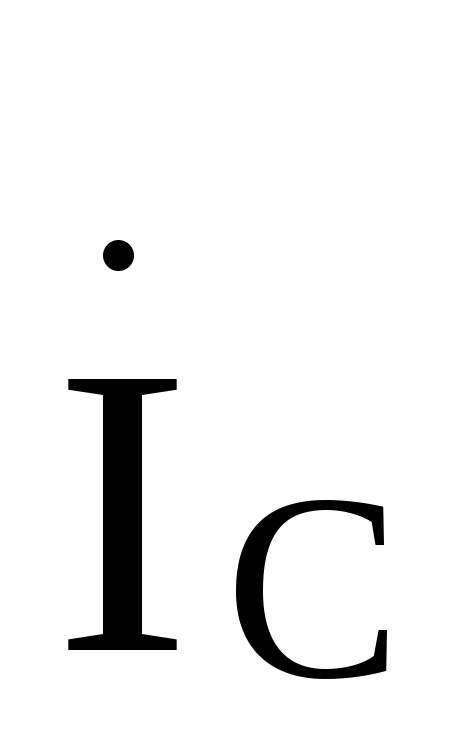 определяются через фазные по первому
закону Кирхгофа:
определяются через фазные по первому
закону Кирхгофа:
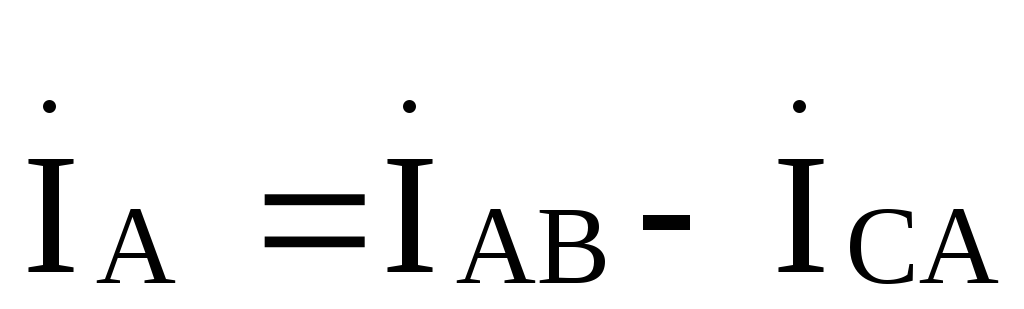 ,
,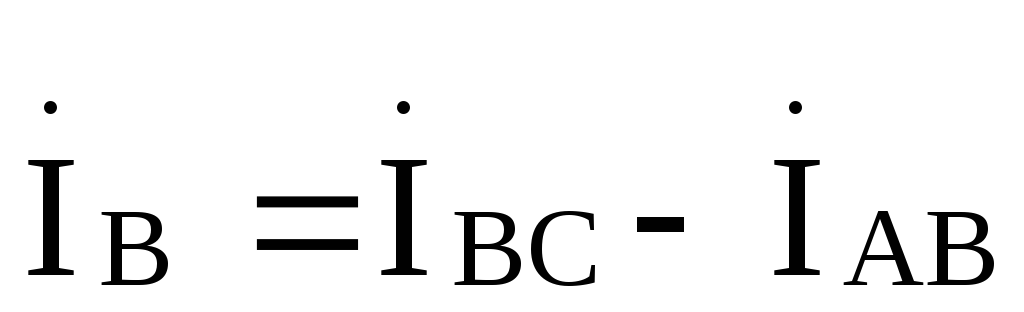 ,
,
Покажем, что при симметричной нагрузке
линейный ток в 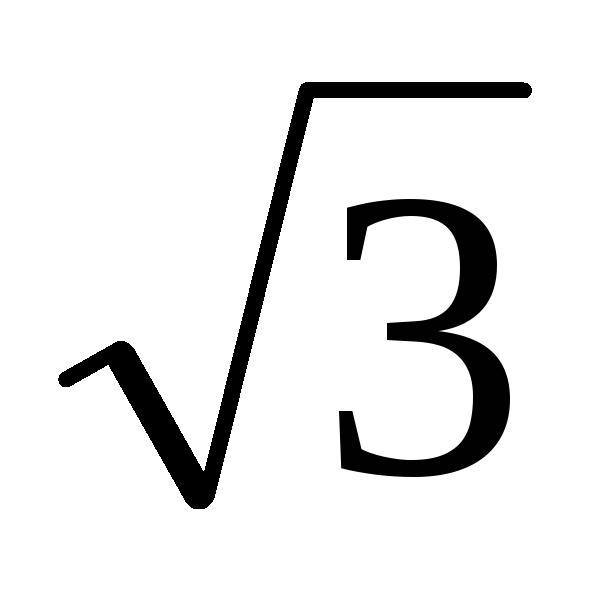 раз больше фазного,
раз больше фазного,
т. е. 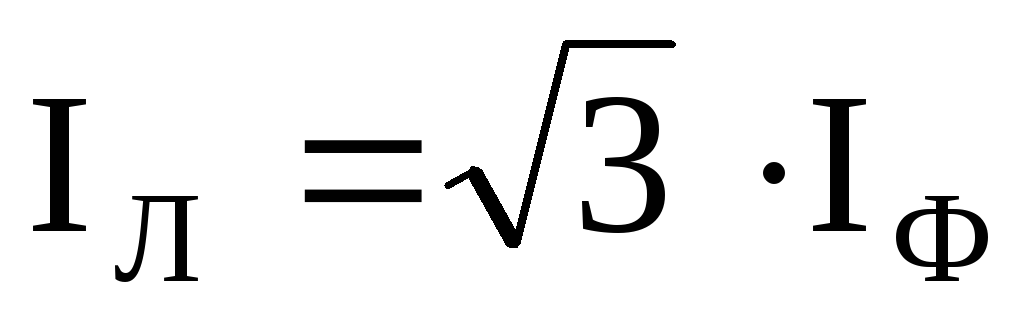
Таким образом, линейный ток  в
в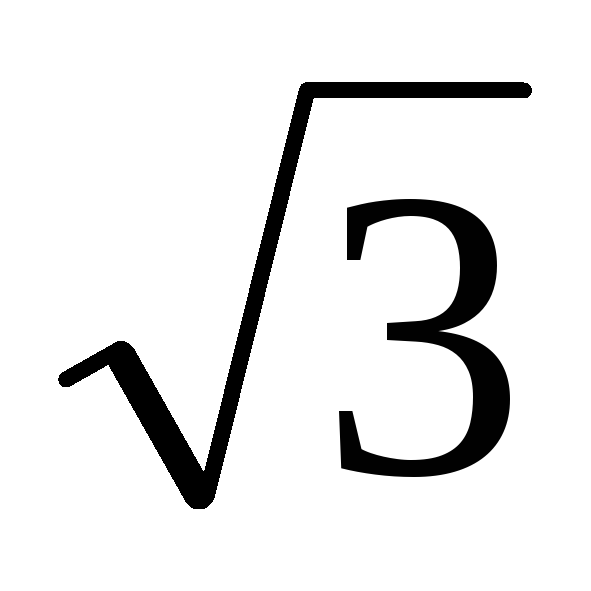 раз больше фазного
раз больше фазного и на 30°отстает от него.
и на 30°отстает от него.
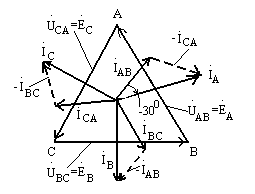
Рис. 9.14
Аналогично можно получить, что линейный
ток  илиотстает соответственно от фазного
илиотстает соответственно от фазного
тока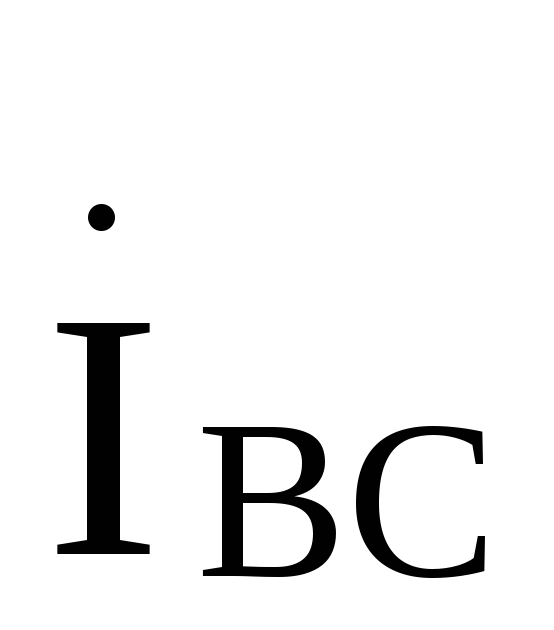 или
или и в
и в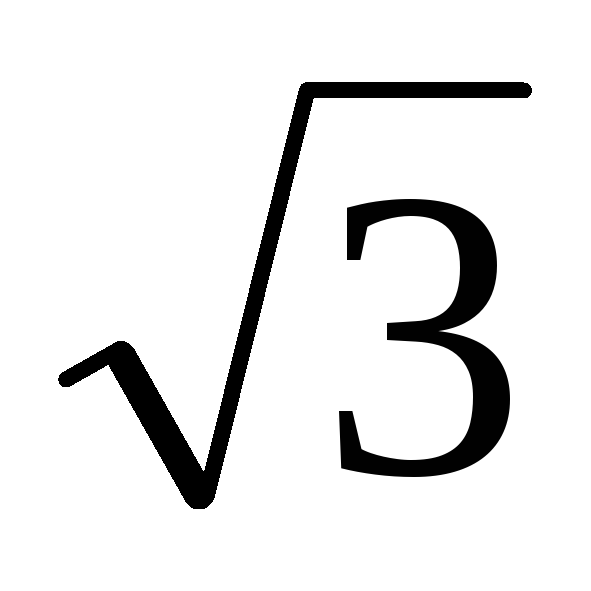 раз больше последнего.
раз больше последнего.
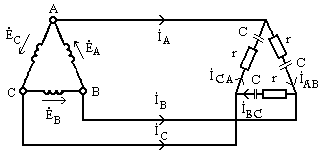
Рис. 9.15
Эти соотношения проще запомнить, если построить векторно-топографическую диаграмму, показанную на рис 9.14.Следует отметить, что фазные токи генератора, если их
положительное направление выбрать совпадающим с положительным направлением ЭДС, будут равны фазным тикам нагрузки одноименных фаз.
Пример 9.2. Вцепи рис. 9.15определить фазные и линейные токи, если r =25Ом, С = 100мкФ
и eA(f)=141sin(400е+30°)В.
Решение
Запишем действующее значение ЭДС фазы Агенератора в комплексной форме
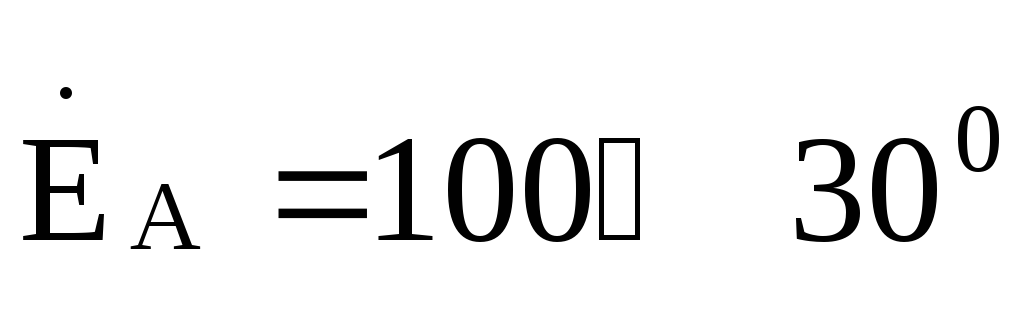 В.
Вычислим емкостное сопротивление
В.
Вычислим емкостное сопротивление
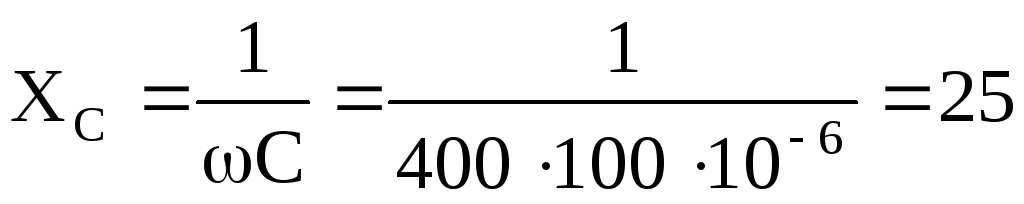 Ом
Ом
Так как 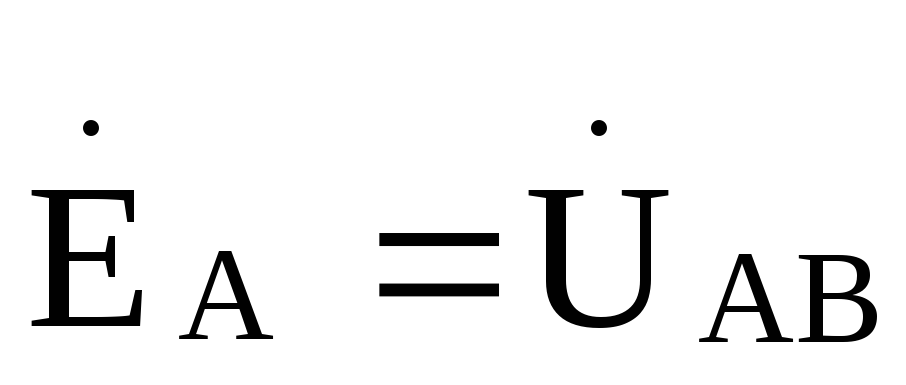 ,
то
,
то
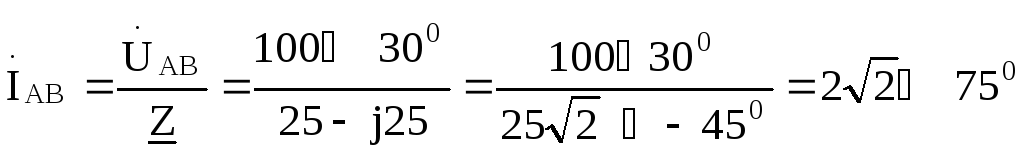 A
A
Ток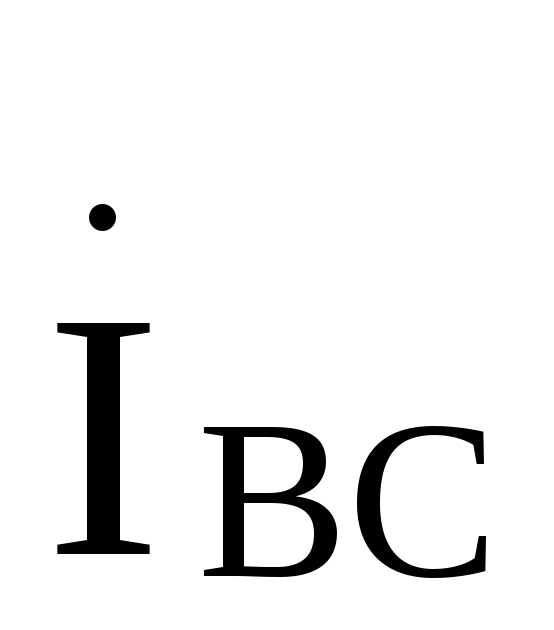 будет отставать от тока
будет отставать от тока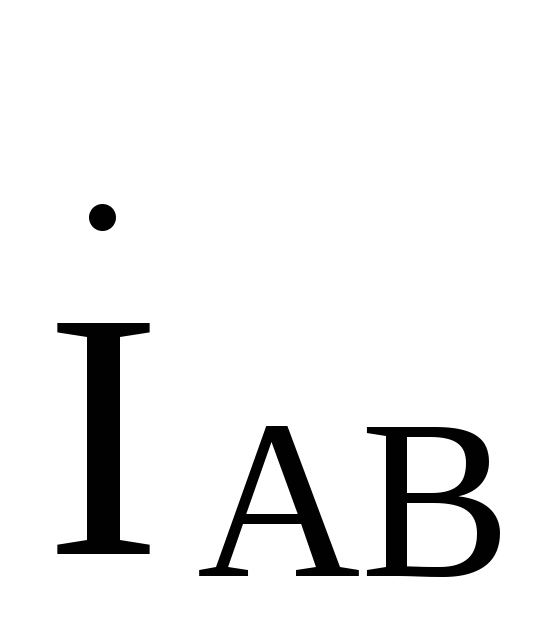 на
120й, а ток
на
120й, а ток будет опережать ток
будет опережать ток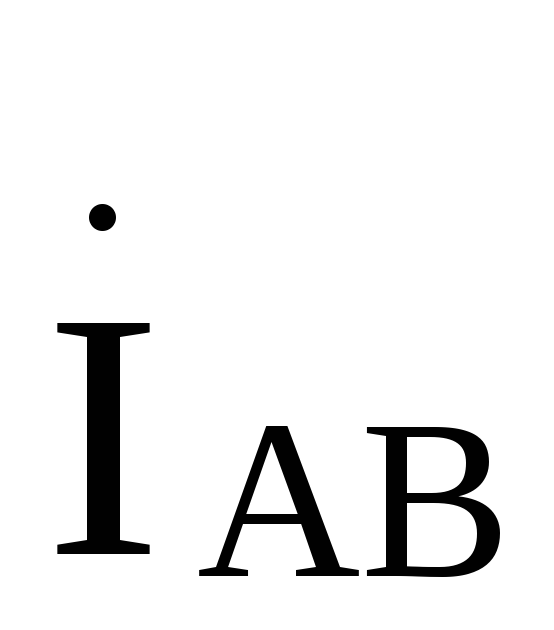 на 120°,поэтому
на 120°,поэтому
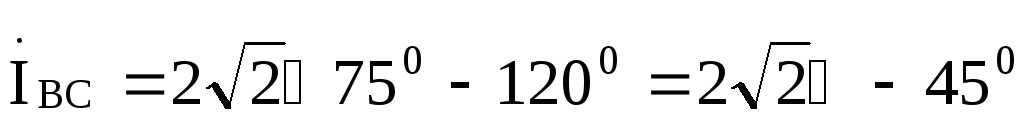 A
A
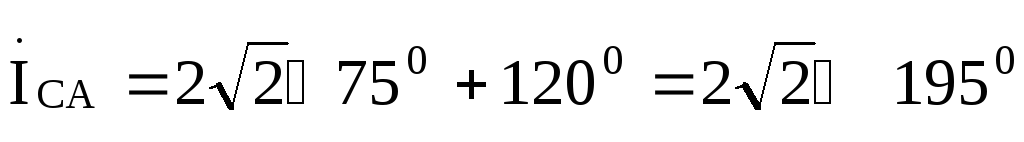 A
A
Линейные токи найдем на основании первого закона Кирхгофа:
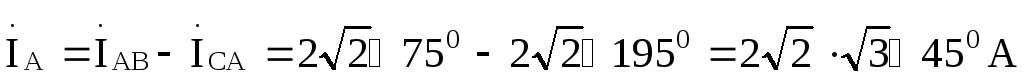
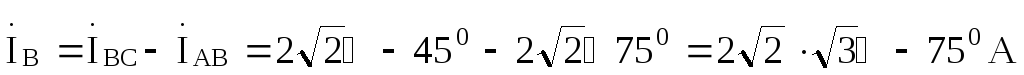
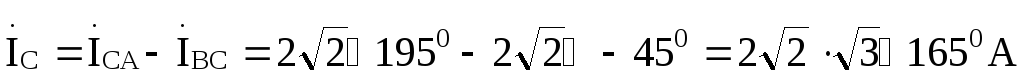
По результатам вычислений построена векторно-топографическая диаграмма,
показанная на рис. 9.16.
3.Обмотки генератора соединены в звезду, а сопротивления нагрузки соединены в треугольник, ‘как показано на рис. 9.17. .
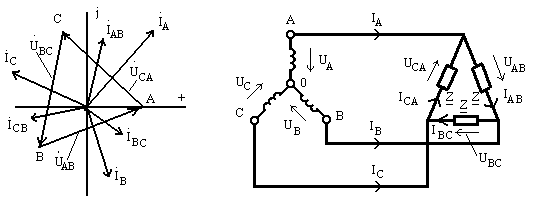
Рис. 9.16 Рис. 9.17
Если принять, что фазная ЭДС фазы Агенератора имеет нулевую начальную
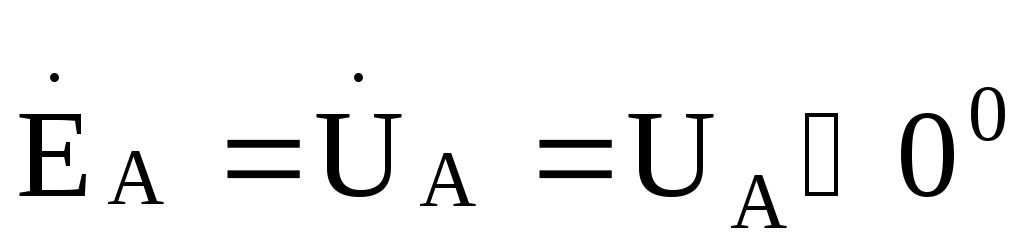 ,то
,то
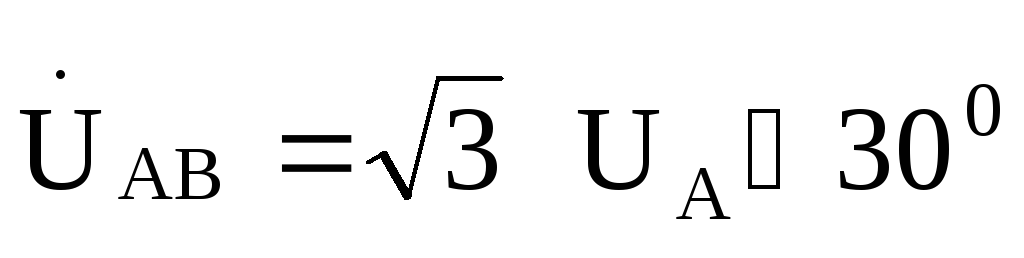
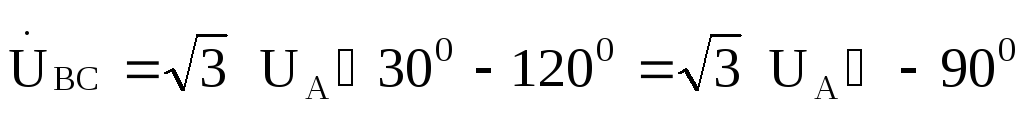
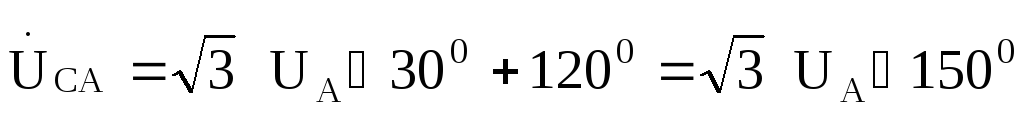
Фазные токи в фазах нагрузки найдем .по закону Ома:
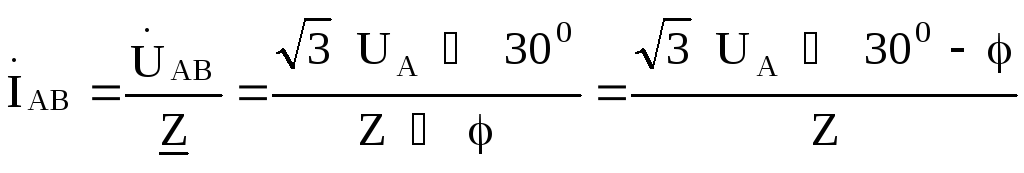
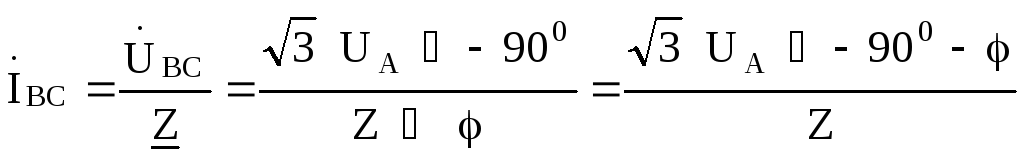
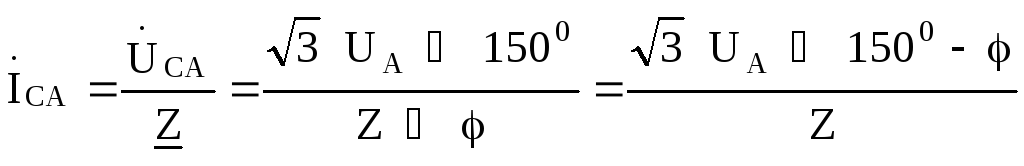
Линейные токи найдем по первому закону Кирхгофа:
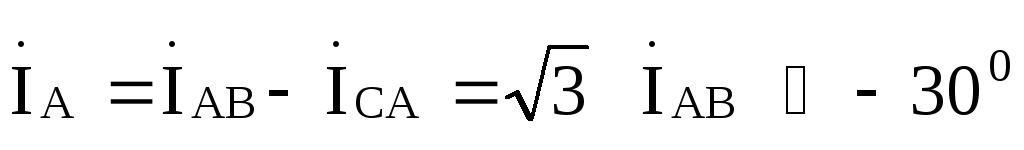
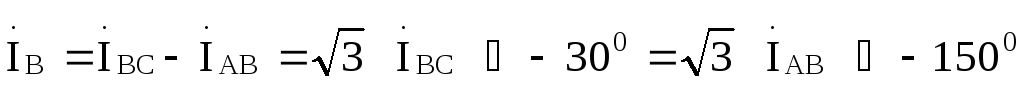
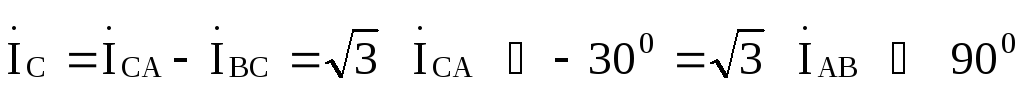
Найденные величины иллюстрируются векторно-топографической диаграммой, приведенной на рис. 9.18,где ось вещественных чисел направлена по вертикали.
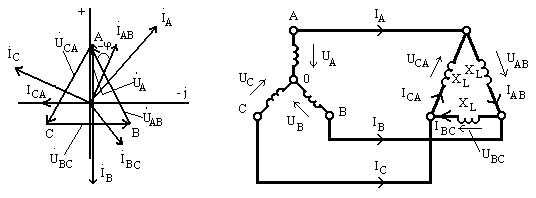
Рис. 9.18Рис. 9.19
Пример 9.3.В цепи
рис. 9.19определить фазные
и линейные токи при ХL=22
Ом и фазном напряжении генератора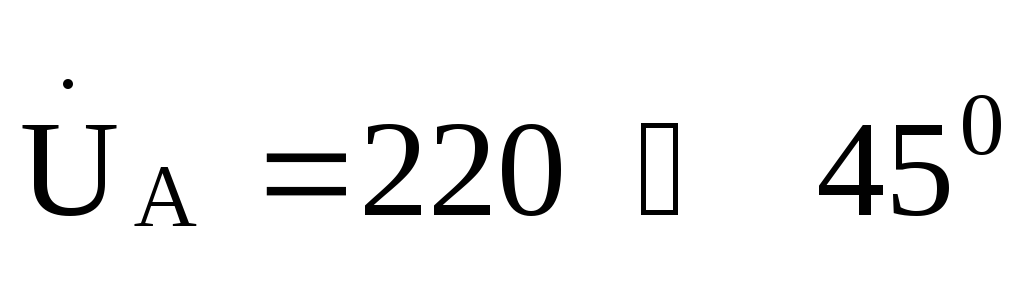 .
.