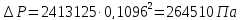Гидравлический расчет трубопроводов Различные способы расчета потерь
Гидравлический расчет трубопроводов 24-14
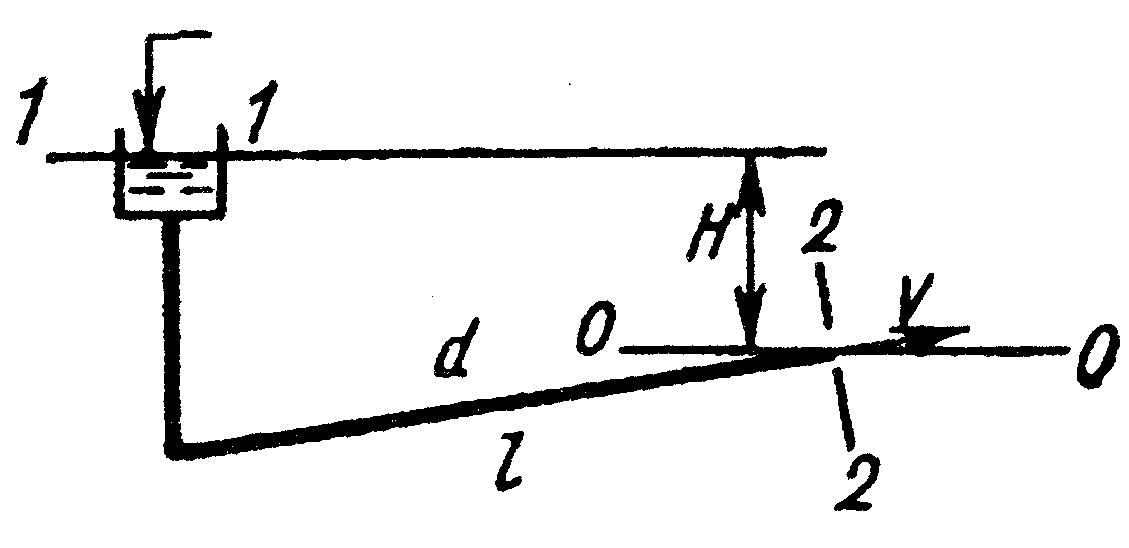
Рассматривается равномерное напорное
движение жидкости в круглой трубе. При
равномерном движении форма и площадь
живого сечения, средняя скорость потока
и эпюра скоростей по длине не изменяются.
В этих условиях живое сечение
характеризуется одним линейным размером
– диаметром. Напомним:  .
.
Общая формула для потерь напора по длине
имеет вид 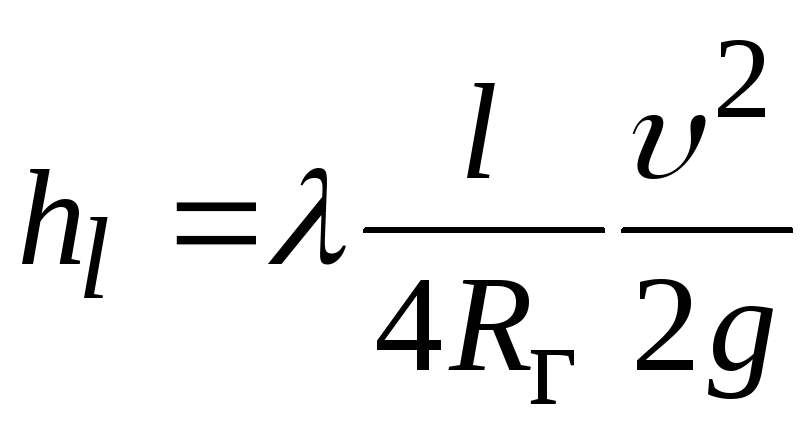 .
.
Для круглых труб 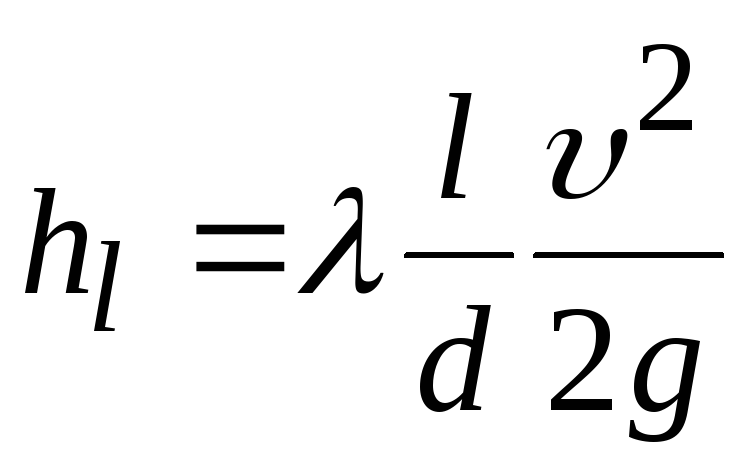 .
.
Это установленная экспериментально формула Дарси-Вейсбаха.
Безразмерный коэффициент
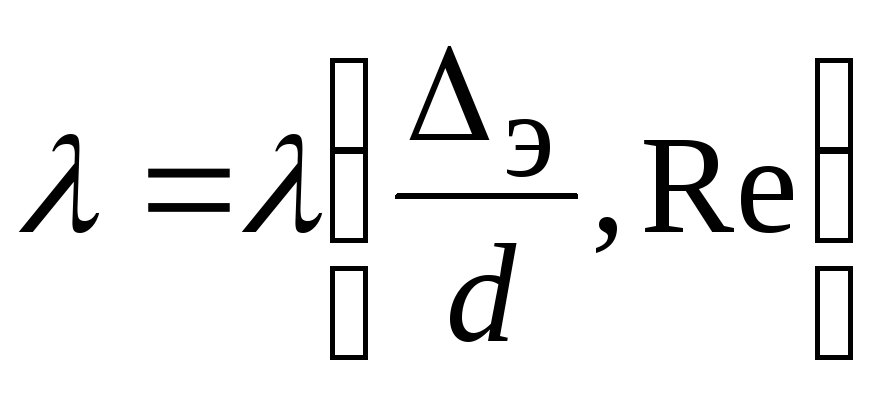 .
Для нахождения
.
Для нахождения существуют эмпирические формулы (режимы
ламинарный – переходный –турбулентный;
область гидравлически гладких труб,
доквадратичная область, квадратичная
область).
существуют эмпирические формулы (режимы
ламинарный – переходный –турбулентный;
область гидравлически гладких труб,
доквадратичная область, квадратичная
область). При равномерном движении жидкости
средняя скорость потока, не изменяющаяся
по длине из формулы  равна
равна .
Обозначим
.
Обозначим .
.
Коэффициент 
 и получимформулу
Шези для средней скорости при равномерном
движении
и получимформулу
Шези для средней скорости при равномерном
движении  ,
где
,
где .
.
Потери напора по длине с учетом
коэффициента Шези 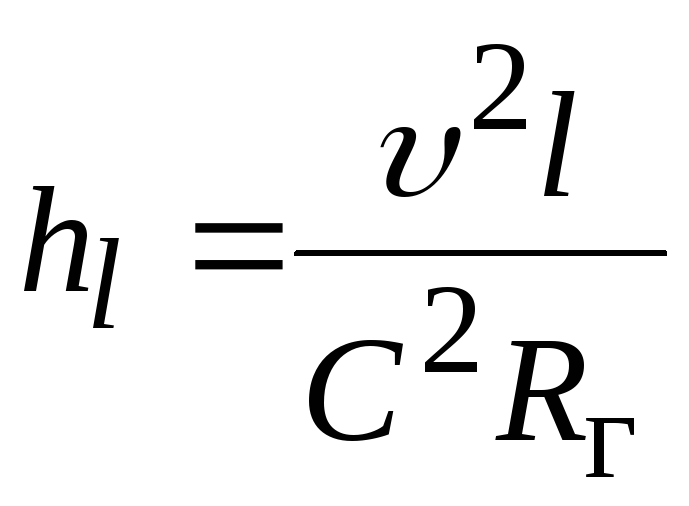 .
.
Коэффициент Шези в отличие от безразмерного
коэффициента Дарси  имеет размерность
имеет размерность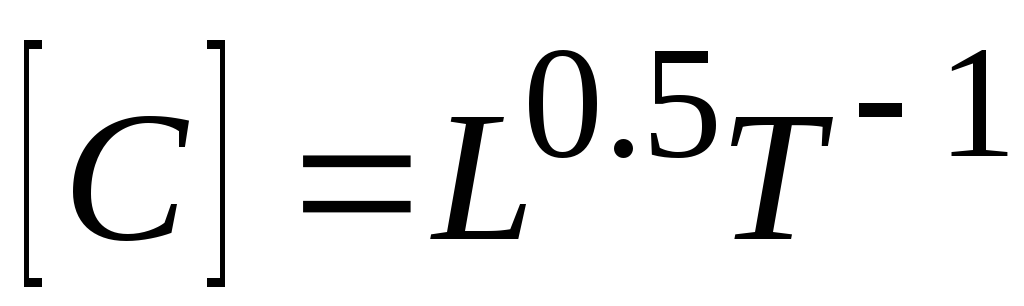 .
В справочниках приводятся таблицы
значений коэффициента Шези для
трубопроводов различного диаметра и
различной шероховатости. Существует
много эмпирических формул для расчета
коэффициента Шези.
.
В справочниках приводятся таблицы
значений коэффициента Шези для
трубопроводов различного диаметра и
различной шероховатости. Существует
много эмпирических формул для расчета
коэффициента Шези.
Зная формулу для средней скорости потока
получим формулу Шези
для расхода при равномерном движении  .
.
При расчете трубопровода обычно
составляют уравнение Бернулли для
потока вязкой жидкости. Пренебрегая
местными потерями и скоростными напорами,
получаем 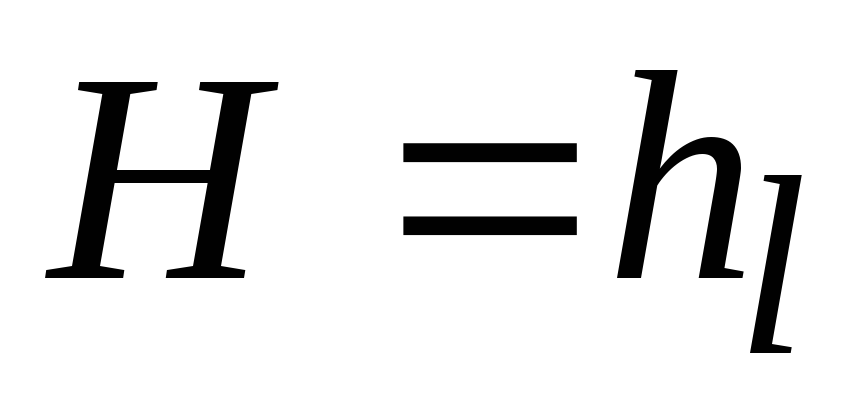 .
.
Вспомним, что гидравлический уклон  ,
откуда
,
откуда .
Подставим найденное значение
гидравлического уклона в формулу Шези
для скорости потока
.
Подставим найденное значение
гидравлического уклона в формулу Шези
для скорости потока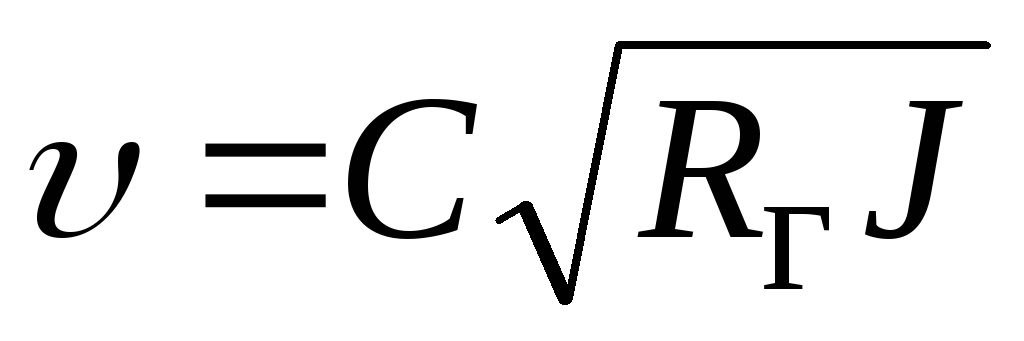

 .
Заметим на будущее, что напор пропорционален
квадрату скорости.
.
Заметим на будущее, что напор пропорционален
квадрату скорости. Запишем формулу Шези для расхода при
равномерном движении  .
.
Объединим параметры, зависящие от
диаметра трубопровода, представим их
виде так называемой расходной
характеристики трубопровода (модуля
расхода) .
.
Расходная характеристика  представляет
собой расход в данной трубе при
гидравлическом уклоне, равном единице.
представляет
собой расход в данной трубе при
гидравлическом уклоне, равном единице.
Тогда расход 
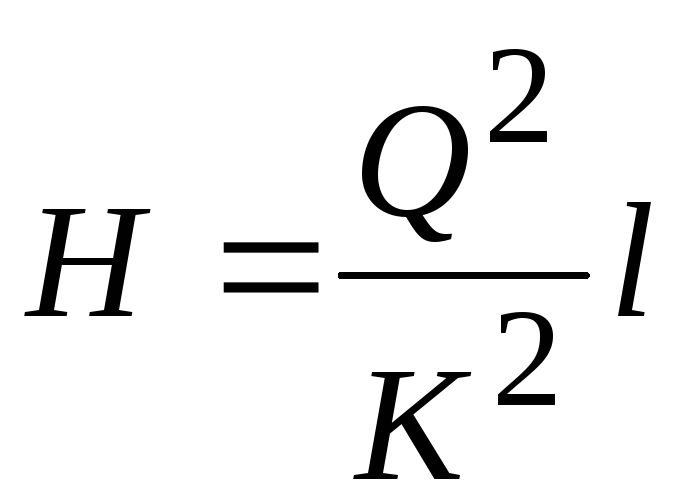 .
. При этом расход  и расходная характеристика
и расходная характеристика должны быть выражены в одних и тех же
единицах. В таблицах для гидравлических
расчетов приводятся значения расходной
характеристики
должны быть выражены в одних и тех же
единицах. В таблицах для гидравлических
расчетов приводятся значения расходной
характеристики для трубопроводов различного диаметра
с различной относительной шероховатостью.
На этой основе производится расчет
трубопроводов «с использованием таблиц».
для трубопроводов различного диаметра
с различной относительной шероховатостью.
На этой основе производится расчет
трубопроводов «с использованием таблиц».
Получим значение  расчетным путем. Гидравлический уклон
равен 1, значит потери равны длине
расчетным путем. Гидравлический уклон
равен 1, значит потери равны длине .
Потери по длине
.
Потери по длине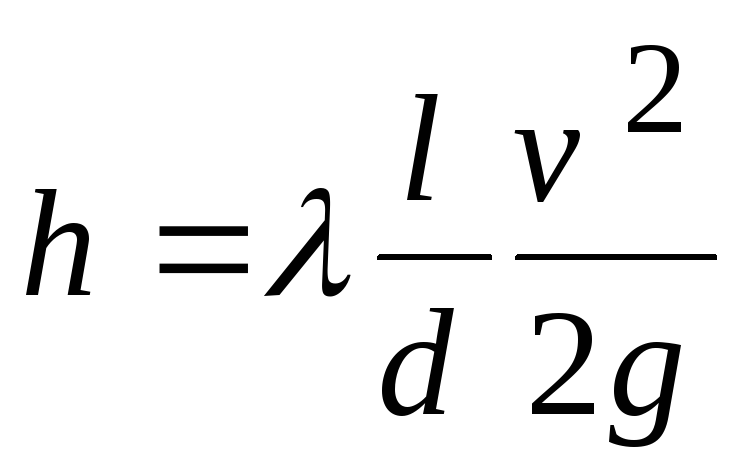

 ;
;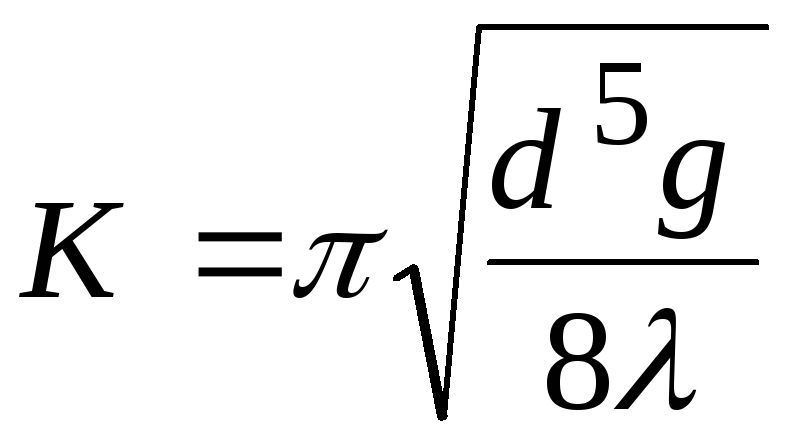 .
. В квадратичной области турбулентного
режима 
Замечание. При равномерном движении гидравлический и пьезометрический уклоны равны. Пренебрегая скоростным напором, получим, что линия полного напора и пьезометрическая лини совпадают.
Классификация трубопроводов
Простой трубопровод – трубопровод, не имеющий ответвлений и состоящий из труб одинакового диаметра, выполненных из одного материала.
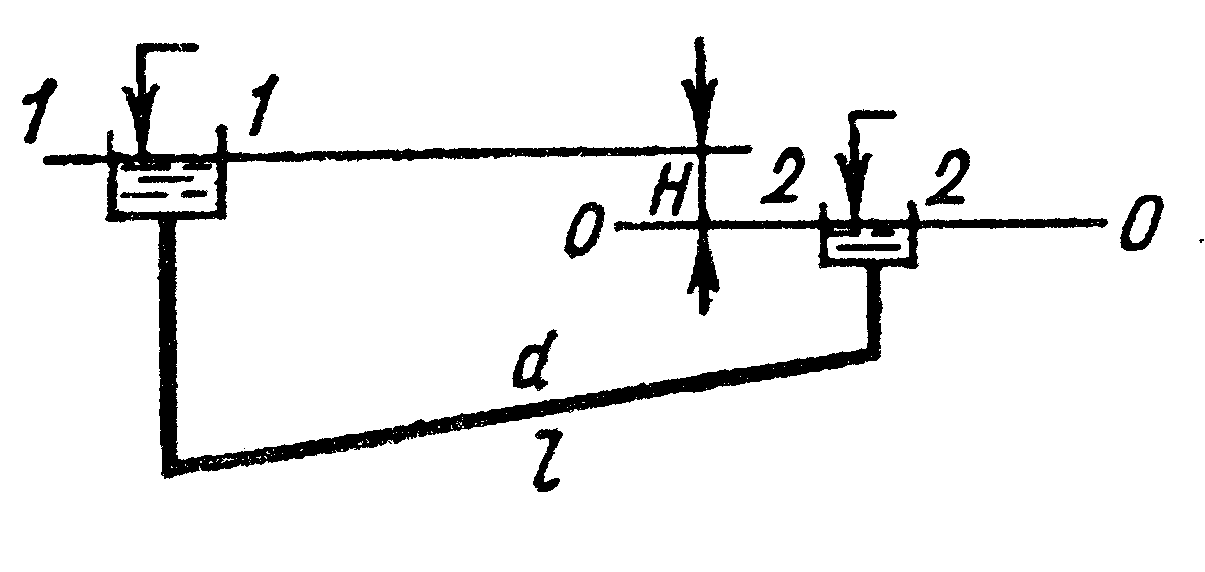
Приведем два примера простых трубопроводов.
 |
|
Движение жидкости в трубе обусловлено
напором  ,
равным разности напоров в резурвуаре-питателе
и приемнике или разности напоров в
резервуаре питателе и в струе на выходе
из трубы, если резервуар-приемник
отсутствует. Если указанная разность
напоров не изменяется во времени, то
движение установившееся. Мы рассматриваем
расчет только трубопроводов с
установившимся движением.
,
равным разности напоров в резурвуаре-питателе
и приемнике или разности напоров в
резервуаре питателе и в струе на выходе
из трубы, если резервуар-приемник
отсутствует. Если указанная разность
напоров не изменяется во времени, то
движение установившееся. Мы рассматриваем
расчет только трубопроводов с
установившимся движением.
Потери напора в трубопроводе можно
рассматривать как сумму потерь на трение
по длине трубопровода и потерь в местных
сопротивлениях  .
.
По соотношению потерь по длине и в местных сопротивлениях в общей величине потерь трубопроводы делятся на гидравлически короткие и гидравлически длинные.
В гидравлически длинном (или просто длинном)трубопроводепотери напора по длине настолько превышают местные потери (и скоростной напор), что местные потери не вычисляют, а принимают как некоторую часть потерь по длине.
Практически при расчете длинных
трубопроводов находят потери напора
по длине  ,
а затем суммарные местные потери напора
учитывают, увеличивая найденное значение
,
а затем суммарные местные потери напора
учитывают, увеличивая найденное значение на
на %.
%.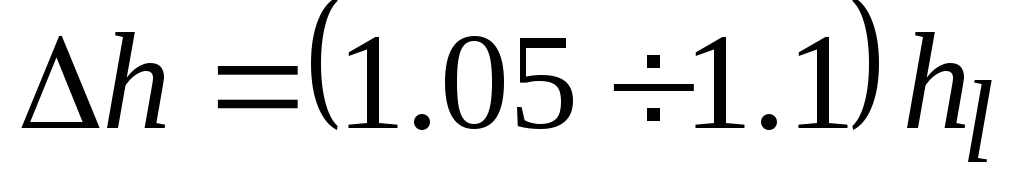 .
.
В гидравлически коротком трубопроводе потери напора по длине и местные потери сопоставимы по значению. При гидравлическом расчете коротких трубопроводов учитывают как местные потери напора, так и потери по длине, а в балансе напоров учитывают скоростные напоры в сечениях потока.
Гидравлические потери — Википедия
Гидравлические потери или гидравлическое сопротивление — безвозвратные потери удельной энергии (переход её в теплоту) на участках гидравлических систем (систем гидропривода, трубопроводах, другом гидрооборудовании), обусловленные наличием вязкого трения[1][2]. Хотя потеря полной энергии — существенно положительная величина, разность полных энергий на концах участка течения может быть и отрицательной (например, при эжекционном эффекте).
Гидравлические потери принято разделять на два вида:
- местные гидравлические потери — обусловлены т. н. местными гидравлическими сопротивлениями — изменениями формы и размера канала, деформирующими поток. Примером местных потерь могут служить: внезапное расширение трубы, внезапное сужение трубы, поворот, клапан и т. п.
Гидравлические потери выражают либо в потерях напора Δh{\displaystyle \Delta h} в линейных единицах столба среды, либо в единицах давления ΔP{\displaystyle \Delta P}: Δh=ΔPρg{\displaystyle \Delta h={\Delta P \over \rho g}}, где ρ{\displaystyle \rho } — плотность среды, g — ускорение свободного падения.
Во многих случаях приближённо можно считать, что потери энергии при протекании жидкости[3] через элемент гидравлической системы пропорциональны квадрату скорости жидкости[2]. По этой причине удобно бывает характеризовать сопротивление безразмерной величиной ζ[4], которая называется коэффициент потерь или коэффициент местного сопротивления и такова, что
- Δp=ζρw22, Δh=ζw22g.{\displaystyle \Delta p=\zeta {\rho w^{2} \over 2}{\mbox{, }}\Delta h=\zeta {w^{2} \over 2g}{\mbox{.}}}
То есть в предположении, что скорость w по всему сечению потока одинакова, ζ=Δp/eторм, где eторм = ρw²/2 — энергия торможения единицы объёма потока относительно канала. Реально в потоке скорость жидкости не равномерна, в справочной литературе в данных формулах принимается среднерасходная скорость w=Q/F, где Q — объёмный расход, F — площадь сечения, для которого рассчитывается скорость[1]. Таким образом, средняя энергия торможения потока обычно несколько больше ρw²/2, см. Среднее квадратическое.
Для линейных потерь обычно пользуются коэффициентом потерь на трение по длине (также коэффициент Дарси) λ, фигурирующего в формуле Дарси — Вейсбаха[2]
- Δh=λLd⋅w22g{\displaystyle \Delta h=\lambda {\frac {L}{d}}\cdot {w^{2} \over 2g}},
где L — длина элемента, d — характерный размер сечения (для круглых труб это диаметр). Иначе в единицах давления
- Δp=λLd⋅ρw22{\displaystyle \Delta p=\lambda {\frac {L}{d}}\cdot {\rho w^{2} \over 2}};
таким образом, для линейного элемента относительной длины L/d коэффициент сопротивления трения ζтр=λL/d.
Влияние режима течения в трубах на гидравлические потери[править | править код]
Поскольку при турбулентном режиме течения происходит расход энергии потока на преодоление вязкости при турбулентных колебаниях, гидравлические потери при ламинарном режиме течения жидкости значительно меньше, чем при турбулентном. Так, например, если бы в системах водоснабжения и отопления при существующих скоростях движения жидкостей возможно было бы поддерживать ламинарный режим течения, то напор насосов можно было бы уменьшить в 5—10 раз[источник не указан 2800 дней]. Изменение режима течения с ламинарного на турбулентный вызывает скачкообразное увеличение сопротивления (при некоторых скоростях, т.е. в некотором диапазоне чисел Рейнольдса, ламинарное течение неустойчиво, но в определённых условиях может существовать). В то же время коэффициент гидравлического сопротивления при ламинарном режиме обычно получается больше, чем при турбулентном, поскольку для ламинарных режимов характерны более низкие скорости. При ламинарном режиме сопротивление примерно линейно зависит от скорости (соответственно, коэффициент примерно линейно падает, например, в круглых трубах λ=64Re{\displaystyle \lambda ={\frac {64}{\mathrm {Re} }}}). При турбулентном режиме в гидравлически гладких трубах (при небольших шероховатостях и небольших Re) зависимость имеет иной характер (для круглых труб λ=0,3164Re4.{\displaystyle \lambda ={\frac {0,3164}{\sqrt[{4}]{\mathrm {Re} }}}.}) и во всех практически реализуемых случаях лежит выше зависимости для ламинарного режима; при бо́льших числах Рейнольдса под влиянием шероховатости график λ претерпевает сложный изгиб, и начиная с некоторого критического значения при Re>Reкр (область автомодельности) λ зависит только от шероховатости.
На преодоление гидравлических потерь в различных технических системах затрачивается работа таких устройств, как насосы, воздуходувки.
Для уменьшения гидравлических потерь рекомендуется в конструкциях гидрооборудования избегать применения деталей, способствующих резкому изменению направления потока — например, заменять внезапное расширение трубы постепенным расширением (диффузор), придавать телам, движущимся в жидкостях, обтекаемую форму и др. Даже в абсолютно гладких трубах имеются гидравлические потери[2]; при ламинарном режиме шероховатость мало на них влияет, однако при обычных в технике турбулентных режимах её увеличение, как правило, вызывает рост гидродинамического сопротивления.
Иногда, напротив, требуется ввести гидравлическое сопротивление в поток. Для этого применяются дроссельные шайбы, редукционные установки, регулирующие клапаны. По измерению давления на некотором элементе, график коэффициента гидравлического сопротивления которого известен, можно узнать скорость потока в некоторых распространённых типах расходомеров.
- ↑ 1 2 Идельчик И. Е. Справочник по гидравлическим сопротивлениям/ Под ред. М. О. Штейнберга. — 3-е изд., перераб. и доп.— М.: Машиностроение, 1992. — C. 10
- ↑ 1 2 3 4 Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов / Т. М. Башта, С. С. Руднев, Б. Б. Некрасов и др.. — 2-е изд., перераб.. — М.: Машиностроение, 1982. — С. 48—50, 84, 88.
- ↑ В гидродинамике жидкостью называется любая текучая среда, как капельная жидкость, так и газ.
- ↑ Также применяется обозначение ξ; буквы часто путают, иногда применяют для различения того, во входном или выходном сечении элемента измерялась скорость в формуле (для расширяющихся или сужающихся элементов).
Расчет гидравлических потерь
Потери давления
в гидролинии слагаются из потерь на
гидравлическое трение  ,
потерь на местное сопротивление
,
потерь на местное сопротивление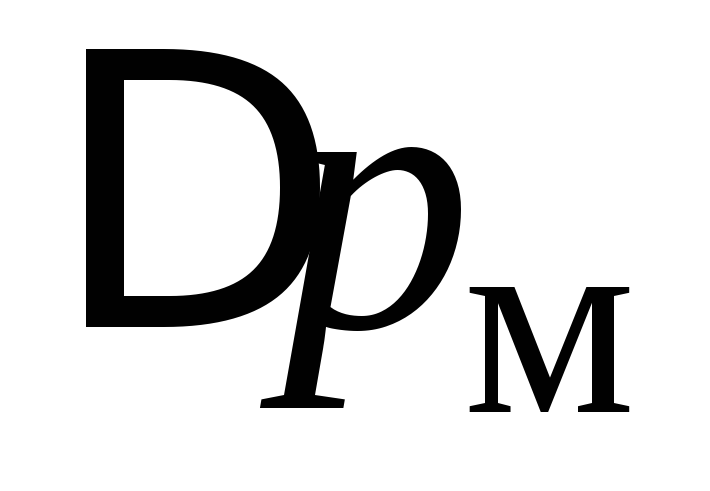 и потери в гидроаппаратуре
и потери в гидроаппаратуре находящихся в данной линии.
находящихся в данной линии.
Потери давления на трение в гидролиниях определяем по формуле:
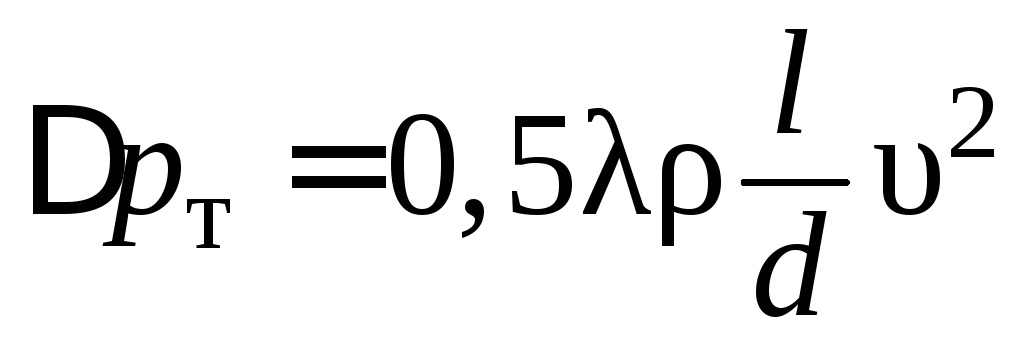 , (6.21)
, (6.21)
где 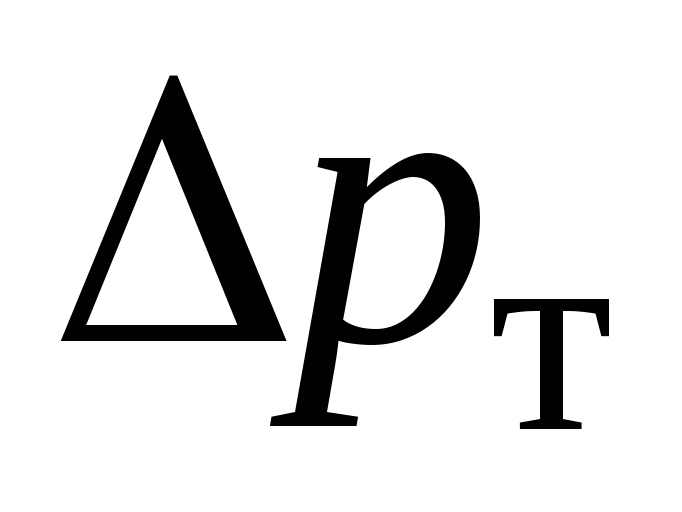 — потери давления, Па;
— потери давления, Па;
d — диаметр трубопровода, м;
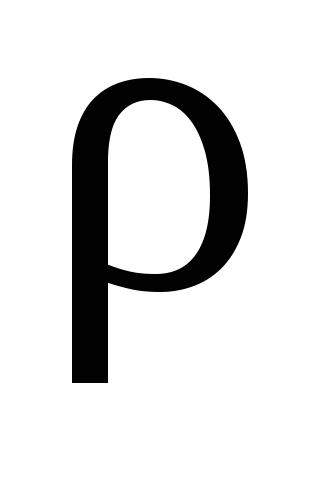 —плотность рабочей
жидкости, кг/м
—плотность рабочей
жидкости, кг/м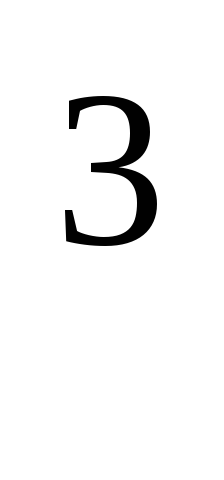 ;
;
 —коэффициент
гидравлического трения;
—коэффициент
гидравлического трения;
 —длина
соответствующего участка гидролинии,
м;
—длина
соответствующего участка гидролинии,
м;
 —средняя скорость
движения рабочей жидкости, м/с.
—средняя скорость
движения рабочей жидкости, м/с.
Для определения
коэффициента гидравлического трения  необходимо определить режим движения
жидкости по формуле:
необходимо определить режим движения
жидкости по формуле:
 , (6.22)
, (6.22)
где  — средняя скорость рабочей жидкости,
см/с;
— средняя скорость рабочей жидкости,
см/с;
 —внутренний
диаметр трубопровода, см;
—внутренний
диаметр трубопровода, см;
 —кинетический
коэффициент вязкости рабочей жидкости,
см2/с,
приложение 29.
—кинетический
коэффициент вязкости рабочей жидкости,
см2/с,
приложение 29.
При ламинарном
режиме движения ( <2300)
коэффициент гидравлического трения
следует определять по формуле
<2300)
коэффициент гидравлического трения
следует определять по формуле ,
для резиновых рукавов РВД
,
для резиновых рукавов РВД .
.
При турбулентном
режиме движения жидкости (2300< <8000)
можно рекомендовать формулу Блазиуса:
<8000)
можно рекомендовать формулу Блазиуса:
 . (6.23)
. (6.23)
При 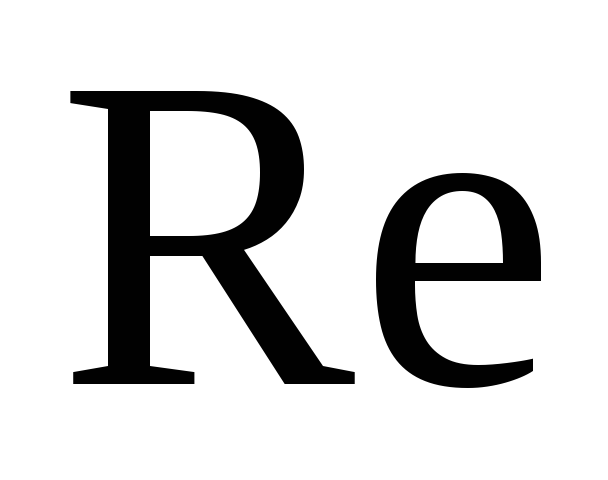 >8000
для жидкостей с высокой вязкостью
коэффициент гидравлического трения
>8000
для жидкостей с высокой вязкостью
коэффициент гидравлического трения не зависит от
не зависит от и его можно принять в практических
расчетах для стальных трубопроводов и
РВД
и его можно принять в практических
расчетах для стальных трубопроводов и
РВД
Потери давления на местные сопротивления определяются по формуле:
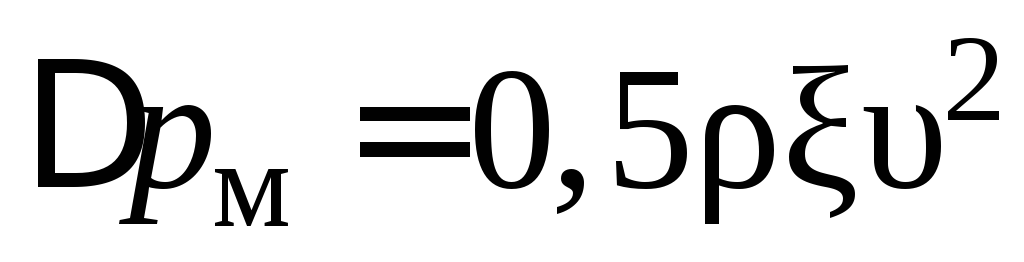 , (6.24)
, (6.24)
где 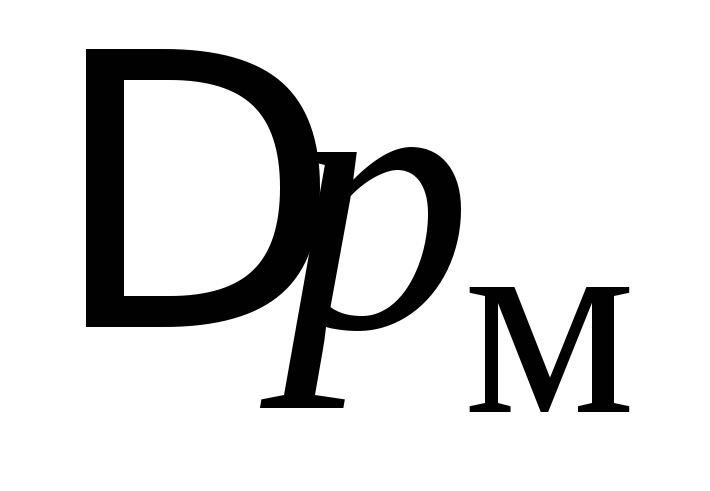 — потери давления, Па;
— потери давления, Па;
 —плотность рабочей
жидкости, кг/м
—плотность рабочей
жидкости, кг/м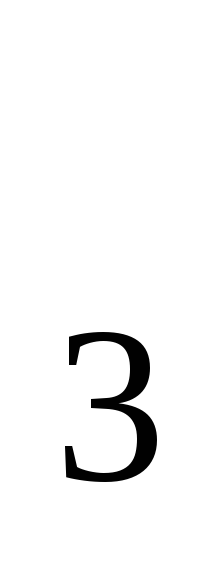 ;
;
ξ — коэффициент местных сопротивлений;
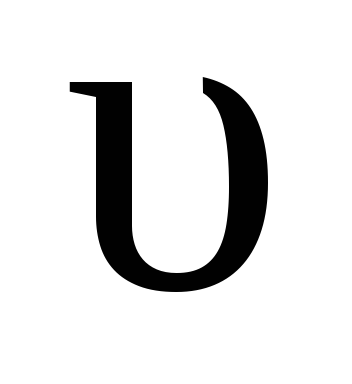 —скорость
жидкости
за местным сопротивлением, м/с.
—скорость
жидкости
за местным сопротивлением, м/с.
Значения коэффициентов местных сопротивлений представлены в приложении 36.
Потери давления в гидроаппаратуре принимаем по техническим характеристикам.
Расчет мощности и кпд гидропривода
Полная мощность гидропривода равна мощности потребляемой насосом и определяется по формуле:
 , (6.25)
, (6.25)
где  — подача насоса;
— подача насоса;
 —давление,
развиваемое насосом;
—давление,
развиваемое насосом;
 —КПД насоса.
—КПД насоса.
КПД гидравлической системы гидропривода определяется по формуле:
 , (6.26)
, (6.26)
где  ,
, ,
, — полезный перепад давления, рабочий
расход жидкости, время работы в течение
каждого цикла исполнительного органа;
— полезный перепад давления, рабочий
расход жидкости, время работы в течение
каждого цикла исполнительного органа;
 —давления настройки
предохранительного клапана;
—давления настройки
предохранительного клапана;
 —подача насоса;
—подача насоса;
 —время цикла.
—время цикла.
Контрольно-регулирующие, направляющие гидроаппараты и вспомогательные элементы. Назначение и классификация гидроаппаратов
При разработке схем объемного гидропривода важным является правильный выбор контрольно-регулирующих, направляющих гидроаппаратов и вспомогательных элементов. В общем случае гидроаппарат — устройство, предназначенное для изменения или поддержания необходимого постоянного давления или расхода рабочей жидкости, а также для изменения направления движения рабочей жидкости в системе гидропривода.
К регулирующим гидроаппаратам относятся предохранительные, переливные, редукционные клапаны, дроссели, делители, сумматоры и регуляторы потока.
К направляющим гидроаппаратам относятся обратные клапана, гидрозамки, разрывные муфты.
К вспомогательным элементам относятся фильтры, теплообменники и гидробаки.
Гидравлический расчет простых трубопроводов
6.5. Гидравлический удар
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено мгновенное закрытие крана (рис. 6.10, а).
Рис. 6.10. Стадии гидравлического удара
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в соответствии с увеличением давления на величину ΔPуд, которое называется ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной. Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе, а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное давление P0 (рис. 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию, соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию, и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная ударная волна под давлением P0 — ΔPуд, которая направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл гидравлического удара повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Если давление P0 невелико (P0 P уд), то картина изменения амплитуды давления получается несколько иная, примерно такая, как показано на рис. 6.11, б.
Рис. 6.11. Изменение давления по времени у крана
Повышение давления при гидравлическом ударе можно определить по формуле
ΔPуд = ρυ0c
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c определится по формуле:
где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = , то скорость ударной волны определится из выражения
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.
6.6. Изменение пропускной способности трубопроводов в процессе их эксплуатации
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по формуле:
kt = k0 + αt
где k0 — абсолютная шероховатость для новых труб, (мм),
kt — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).
Таблица 6.1
Проверить себя ( Тест )
Наверх страницы
Гидравлическое сопротивление. Расчет в Excel.
Опубликовано 24 Июн 2018
Рубрика: Теплотехника | 19 комментариев
Выполнение расчета гидравлического сопротивления отдельного трубопровода и всей системы в комплексе является ключевой задачей в гидравлике, решение которой позволяет подобрать сечения труб и насос с необходимыми значениями давления и расхода в рабочем режиме.
В одной из ранних статей на блоге рассмотрен простой пример расчета трубопровода с параллельными участками с использованием понятия «характеристика сопротивления». В конце статьи я анонсировал: «Можно существенно повысить точность метода…». Под этой фразой подразумевалось учесть зависимость характеристик сопротивления от расхода более точно. В том расчете характеристики сопротивлений выбирались из таблиц по диаметру трубы и по предполагаемому расходу. Полковов Вячеслав Леонидович написал взамен таблиц пользовательские функции в Excel для более точного вычисления гидравлических сопротивлений, которые любезно предоставил для печати. Термины «характеристика сопротивления» и «гидравлическое сопротивление» обозначают одно и то же.
Краткая теория.
В упомянутой выше статье теория вкратце рассматривалась. Освежим в памяти основные моменты.
Движение жидкостей по трубам и каналам сопровождается потерей давления, которая складывается из потерь на трение по длине трубопровода и потерь в местных сопротивлениях – в изгибах, отводах, сужениях, тройниках, запорной арматуре и других элементах.
В гидравлике в общем случае потери давления вычисляются по формуле Вейсбаха:
∆Р=ζ·ρ·w²/2, Па, где:
- ζ – безразмерный коэффициент местного сопротивления;
- ρ – объёмная плотность жидкости, кг/м3;
- w – скорость потока жидкости, м/с.
Если с плотностью и скоростью всё более или менее понятно, то определение коэффициентов местных сопротивлений – достаточно непростая задача!
Как было отмечено выше, в гидравлических расчетах принято разделять два вида потерь давления в сетях трубопроводов.
- В первом случае «местным сопротивлением» считается трение по длине прямого участка трубопровода. Перепад давления для потока в круглой трубе рассчитывается по формуле Дарси-Вейсбаха:
∆Ртр=ζтр·ρ·w²/2=λ·L·ρ·w²/(2·D), Па, где:
- L – длина трубы, м;
- D – внутренний диаметр трубы, м;
- λ – безразмерный коэффициент гидравлического трения (коэффициент Дарси).
Таким образом, при учете сопротивления трению коэффициент потерь – коэффициент местного сопротивления – и коэффициент гидравлического трения связаны для круглых труб зависимостью:
ζтр=λ·L/D
- Во втором случае потери давления в местных сопротивлениях вычисляются по классической формуле Вейсбаха:
∆Рм=ζм·ρ·w²/2, Па
Коэффициенты местных сопротивлений определяются для каждого вида «препятствия» по индивидуальным эмпирическим формулам, полученным из практических опытов.
Выполним ряд математических преобразований. Для начала выразим скорость потока через массовый расход жидкости:
w=G/(ρ·π·D²/4), м/с, где:
- G – расход жидкости, кг/с;
- π – число Пи.
Тогда:
∆Ртр=8·λ·L·G²/(ρ·π²·D5), Па;
∆Рм=8·ζм·G²/(ρ·π²·D4), Па.
Введем понятие гидравлических сопротивлений:
Sтр=8·λ·L·/(ρ·π²·D5), Па/(кг/с)²;
Sм=8·ζм·/(ρ·π²·D4), Па/(кг/с)².
И получим удобные простые формулы для вычисления потерь давления при прохождении жидкости в количестве G через эти гидравлические сопротивления:
∆Ртр=Sтр·G², Па;
∆Рм=Sм·G², Па.
Размерность гидравлического сопротивления (Па/(кг/с)²) определена массовой скоростью (кг/с) движения жидкости, а физические процессы в транспортных системах зависят от её объёмной скорости (м3/с), что учтено в формулах присутствием объёмной плотности ρ транспортируемой жидкости.
Для удобства последующих расчётов целесообразно введение понятия «гидравлическая проводимость» — а.
Для последовательного и параллельного соединений гидравлических сопротивлений справедливы формулы:
Sпосл=S1+S2+…+Sn, Па/(кг/с)²;
Sпар=1/(а1+a2+…+an)², Па/(кг/с)²;
ai=(1/Si)0,5, (кг/с)/Па0,5.
Коэффициент гидравлического трения.
Для определения гидравлического сопротивления от трения о стенки трубы Sтр необходимо знать параметр Дарси λ – коэффициент гидравлического трения по длине.
В технической литературе приводится значительное количество формул разных авторов, по которым выполняется вычисление коэффициента гидравлического трения в различных диапазонах значений числа Рейнольдса.
Обозначения в таблице:
- Re – число Рейнольдса;
- k – эквивалентная шероховатость внутренней стенки трубы (средняя высота выступов), м.
В [1] приведена еще одна интересная формула расчета коэффициента гидравлического трения:
λ=0,11·[(68/Re+k/D+(1904/Re)14)/(115·(1904/Re)10+1)]0,25
Вячеслав Леонидович выполнил проверочные расчеты и выявил, что вышеприведенная формула является наиболее универсальной в широком диапазоне чисел Рейнольдса!
Значения, полученные по этой формуле чрезвычайно близки значениям:
- функции λ=64/Re для зоны ламинарного характера потока в диапазоне 10<Re<1500;
- функции λ=0,11·(68/Re+k/D)0,25для зоны турбулентного характера потока при Re>4500;
- в диапазоне 1500<Re<4500 согласно анализу присутствует переходная зона.
В переходной зоне, согласно опытам Никурадзе, график функции λ=f(Re,D,k) имеет сложную форму. Он представляет собой две сопряженные обратные кривые, которые в свою очередь сопрягаются с одной стороны с кривой гладких труб (ламинарный поток), а с другой стороны с прямыми относительной шероховатости.
Данная зона до конца не изучена, поэтому желательно гидравлические режимы проектируемых систем рассчитывать без захода в эту область: 1500<Re<4500!
На следующем рисунке показаны графики функции λ=f(Re,D,k), построенные по вышеприведенной универсальной формуле. Характер кривых в переходной области соответствует графикам Никурадзе [2, 4].
Пользовательская функция в Excel КтрТрубаВода(Рвода,tвода,G,D,kэ) выполняет расчет коэффициента гидравлического трения λ по рассмотренной универсальной формуле. При этом везде далее kэ=k.
Внимание!
- В зоне переходного характера потока происходит смена знака наклона кривой λ, что может вызвать неработоспособность систем автоматического регулирования!
- ПФ КтрТрубаВода(Pвода,tвода,G,D,kэ) при турбулентном потоке существенно зависит от значения kэ – эквивалентной шероховатости внутренней поверхности трубы. В связи с этим следует обращать внимание на задание объективного значения kэ с учётом используемых при монтаже труб (см. [2] стр.78÷83).
Расчет в Excel гидравлических сопротивлений.
Для облегчения выполнения рутинных гидравлических расчетов Полковов В.Л. разработал ряд пользовательских функций. Перечень некоторых из них, наиболее часто используемых на практике, приведен в таблице ниже.
Некоторые пояснения по аргументам пользовательских функций:
- ГСдиффузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходДиффузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСконфузор(Pвода,tвода,G,Dmin,Dmax,kэ,L) – свободные размеры;
- ГСпереходКонфузор(Pвода,tвода,G,Dmin,Dmax,kэ) – стандартный переход;
- ГСотвод(Pвода,tвода,G,D0,R0,Угол,kэ) – свободные размеры;
- ГСотводГОСТ(Pвода,tвода,G,D,Угол,kэ) – стандартный отвод.
Приведённые пользовательские функции желательно использовать с учётом начального участка транспортирования (расстояния от одного гидравлического сопротивления до следующего гидравлического сопротивления). Это позволяет уменьшить погрешности расчётов, вызванных влиянием «неустановившегося» характера потока жидкости.
Для турбулентных течений длина начального участка должна быть не менее:
Lнач=(7,88·lg (Re) – 4,35)·D
Для ламинарных течений минимальная длина начального участка:
Lнач=B·Re·D
Здесь В=0,029 по данным Буссинекса, и В=0,065 по данным Шиллера, D — внутренний диаметр системы транспортирования.
Далее на скриншоте показана таблица в Excel с примерами расчетов гидравлических сопротивлений.
Литература:
- Черникин А.В. Обобщение расчета коэффициента гидравлического сопротивления трубопроводов // Наука и технология углеводородов. М.: 1998. №1. С. 21–23.
- И.Е. Идельчик, «Справочник по гидравлическим сопротивлениям». 3-е издание, переработанное и дополненное. Москва, «Машиностроение», 1992.
- А.Д. Альтшуль, «Гидравлические сопротивления», издание второе, переработанное и дополненное. Москва, «НЕДРА», 1982.
- Б.Н. Лобаев, д.т.н., профессор, «Расчёт трубопроводов систем водяного и парового отопления». Государственное издательство литературы по строительству и архитектуре. УССР, Киев, 1956.
Ссылка на скачивание файла: gidravlicheskie-soprotivleniya (xls 502,0KB).
Другие статьи автора блога
На главную
Статьи с близкой тематикой
Отзывы
МЕТОДИКА РАСЧЕТА ГИДРАВЛИЧЕСКИХ ПОТЕРЬ В ЭЛЕМЕНТАХ САНИРОВАННЫХ ТРУБОПРОВОДОВ | Опубликовать статью РИНЦ
Савинцева Ю.И.1, Сенаторова Е.В.2, Смирнов А.И.3, Шабалин М.В.4, Хазиев Р.А.5
1,2,3,4,5 Ведущий специалист ЗАО НДЦ «Русская лаборатория», Санкт-Петербург
МЕТОДИКА РАСЧЕТА ГИДРАВЛИЧЕСКИХ ПОТЕРЬ В ЭЛЕМЕНТАХ САНИРОВАННЫХ ТРУБОПРОВОДОВ
Аннотация
В статье рассматривается изменение гидравлического режима в элементах санированных трубопроводов. Представлен метод расчета снижения гидравлических потерь в санированных элементах трубопроводов. Произведена оценка снижения гидравлических потерь в элементах трубопроводов после санации.
Ключевые слова: санация трубопроводов, гидравлические потери, методы расчета.
Savinceva Ju.I.1, Senatorova E.V.2, Smirnov A.I.3, Shabalin M.V.4, Haziev R.A.5
1,2,3,4,5 Lead specialist of Ltd Russian Laboratory, Saint-Petersburg
THE METHOD FOR PRESSURE LOSSES CALCULATION IN THE SLIPLINED PIPELINES ELEMENTS
Abstract
In the present paper there was considered changing of the hydraulic operation in the sliplined pipelines elements. There was performed the method for calculation of pressure losses decreasing in the sliplined pipelines elements. There was estimated average pressure losses decreasing in the pipelines elements after the sliplining process.
Keywords: pipelines sliplining, pressure losses, calculation methods.
Неизбежное старение трубопроводов тепловых сетей неотрывно связано с процессом их реконструкции. Так, в Санкт-Петербурге ежегодно реконструируется от 50 до 100 км магистральных и квартальных тепловых сетей [5]. Процесс полной реконструкции, как известно, связан с дорогостоящим вскрытием грунта над поверхностью всей теплотрассы и сопутствующим нарушением коммуникаций и благоустройства территории. Кроме того, немаловажным является и тот факт, что полная реконструкция участка тепловой сети при таком подходе в целом ряде случаев может растянуться на несколько лет.
Необходимость снижения издержек для сохранения текущего объема реконструкции тепловых сетей в условиях экономии средств, с одной стороны, и стремление сократить также и сроки реконструкции, с другой, приводят к необходимости поиска новых методов и технологий производства реконструкции. Так, специалистами ОАО «Теплосеть Санкт-Петербурга» активно апробируется технология санации реконструируемых участков теплосетей [3, 6]. Суть этого метода состоит в ведении реконструируемый трубопровод специальной вставки, которая при определенных условиях принимает форму трубопровода и затвердевает. Данный метод позволяет существенно снизить удельные затраты на проведение реконструкции за счет практически полного исключения вскрытия грунта и повысить производительность работ.
При проведении такой процедуры немаловажным остается и факт изменения гидравлического режима в реконструированном участке. С одной стороны, наблюдается некоторое уменьшение проходного сечения трубопровода, что, при равном расходе, приводит к росту гидравлических потерь. С другой стороны, после проведения санации эквивалентная шероховатость трубопровода существенно снижается ([1]), что приводит к снижению гидравлических потерь. Оценка превалирования того или иного эффекта была проведена в [4]. В [4] было показано, что для случая прямолинейного участка после санации трубопровода удается достичь снижения гидравлических потерь более чем в 2 раза. Эквивалентом этого эффекта является возможность уменьшения диаметра санированного трубопровода по отношению к несанированному на 20%. При этом, однако, в работе [4] не затрагивались вопросы изменения гидравлического режима в элементах теплосетей, таких как отводы, колена, переходы диаметров. В этой связи целью настоящей работы является разработка методики и численная оценка снижения гидравлических потерь в элементах тепловых сетей:
- литых и секционных отводах;
- коленах.
Вначале рассмотрим основные соотношения для определения потерь давления в исследуемых элементах, являющимися местными сопротивлениями. Будем придерживаться терминологии, принятой авторами [4]. Потери давления в литом отводе при  выражаются соотношением ([2]):
выражаются соотношением ([2]):
 (1)
(1)
где: R0 – радиус закругления отвода, м; δ – угол поворота в отводе, град.; А – коэффициент, учитывающий влияние угла поворота в отводе; В – коэффициент, учитывающий влияние относительного радиуса закругления  отвода; С – коэффициент, учитывающий влияние относительной вытянутости поперечного сечения отвода (для отвода с круглым поперечным сечением коэффициент равен 1). Коэффициент А в формуле (1) при δ = 90º равен 1, при δ < 70º A ≈ 0,9·sinδ. Коэффициент В в формуле (1) для отводов с
отвода; С – коэффициент, учитывающий влияние относительной вытянутости поперечного сечения отвода (для отвода с круглым поперечным сечением коэффициент равен 1). Коэффициент А в формуле (1) при δ = 90º равен 1, при δ < 70º A ≈ 0,9·sinδ. Коэффициент В в формуле (1) для отводов с  вычисляется в соответствии с выражением:
вычисляется в соответствии с выражением:
 (2)
(2)
Для секционных отводов суммарные потери давления для переходной и квадратичной областей выражаются соотношением ([2]):
 (3)
(3)
где:  для переходной и квадратичной областей принимается равным 2 для несанированного отвода и
для переходной и квадратичной областей принимается равным 2 для несанированного отвода и  для санированного отвода. Коэффициенты местного сопротивления
для санированного отвода. Коэффициенты местного сопротивления  для трехзвенных отводов с углами поворота 45º и 60º равны, соответственно, 0,11 и 0,15. Коэффициенты потерь трения для трехзвенных отводов с углами поворота 45º и 60º определяются следующим образом ([2]):
для трехзвенных отводов с углами поворота 45º и 60º равны, соответственно, 0,11 и 0,15. Коэффициенты потерь трения для трехзвенных отводов с углами поворота 45º и 60º определяются следующим образом ([2]):
 (4)
(4)
 (5)
(5)
Для шероховатых колен круглого поперечного сечения суммарные потери давления выражаются соотношением ([2]):
 (6)
(6)
где:  для переходной и квадратичной областей принимается равным 1,5 для несанированного отвода и
для переходной и квадратичной областей принимается равным 1,5 для несанированного отвода и  для санированного отвода. Величины A и
для санированного отвода. Величины A и  в формуле (6) выражаются следующим образом:
в формуле (6) выражаются следующим образом:
 (7)
(7)
 (8)
(8)
В расчетах снижения гидравлических потерь примем граничные условия и значение эквивалентной шероховатости, использованные авторами [4]. Результаты расчетов снижения гидравлических потерь в санированных элементах тепловых сетей приведены в таблицах 1 – 3. Проанализируем полученные результаты.
Таблица 1. Результаты расчета снижения потерь для литого отвода

Таблица 2. Результаты расчета снижения потерь для секционного отвода

Таблица 3. Результаты расчета снижения потерь для колена

Анализ полученных результатов показывает следующее. Для случая литых отводов снижение потерь достигает существенной величины лишь в случае  .
.
Для секционных отводов с ростом диаметра снижение потерь начинает принимать существенные значения (до 2 раз). Необходимо также отметить, что если для секционных отводов с углами поворота 45º и 60º снижение потерь в санированном отводе монотонно увеличивается с ростом  , то для секционного отвода с углом поворота 90º, очевидно, существует некоторая оптимальная конфигурация отвода, при которой снижение потерь в санированном отводе достигает максимума.
, то для секционного отвода с углом поворота 90º, очевидно, существует некоторая оптимальная конфигурация отвода, при которой снижение потерь в санированном отводе достигает максимума.
Для колен снижение потерь не зависит от угла поворота в колене и определяется диаметром поперечного сечения колена.
Подводя итоги, необходимо отметить, что если для случая прямолинейного участка тепловой сети санация трубопровода позволяет существенно снизить потери давления, то для технологических элементов теплосетей такого эффекта не наблюдается. В этих элементах превалируют потери за счет местных сопротивлений. В этой связи уменьшение диаметра технологических элементов при санации теплосетей не рекомендуется, поскольку может привести к существенному росту гидравлических потерь на всем санируемом участке.
Литература
- Гидравлические потери на трение в водоводах электростанций / А.Д. Альтшуль, Ю.А. Войтинская, В.В. Казеннов, Э.Н. Полякова. М.: Энергоатомиздат, 1985. 104 с.
- Идельчик И.Е. Справочник по гидравлическим сопротивлениям. 3-е изд., перераб. и доп. М.: Машиностроение, 1992. 672 с.
- Николаев А.Э., Сафонов А.А. Санация тепловых сетей методом цементирования // Новости теплоснабжения. 2011. №11 (135). С. 18 – 23.
- О возможности применения новой технологии при ремонтах трубопроводов теплосетей / Файнштейн А.В., Мусиенко Л.В., Самсонова Л.В., Некрасова О.Г. // Журнал международного научного института Educatio. 2015. №6 (13) Часть 2. С. 12 – 14.
- О методах НК, применяемых для диагностики трубопроводов тепловых сетей / Л.В. Поленова, Н.В. Черновец, Н.В. Иванов, Д.Е. Чуйко // В мире неразрушающего контроля. 2009. №4 (46). С. 25 – 28.
- Помаскина Т.И. Перспективный метод // ЖКХ: технологии и оборудование. 2008. №12. С. 30 – 31.
References
- Gidravlicheskie poteri na trenie v vodovodah jelektrostancij / A.D. Al’tshul’, Ju.A. Vojtinskaja, V.V. Kazennov, Je.N. Poljakova. M.: Jenergoatomizdat, 1985. 104 s.
- Idel’chik I.E. Spravochnik po gidravlicheskim soprotivlenijam. 3-e izd., pererab. i dop. M.: Mashinostroenie, 1992. 672 s.
- Nikolaev A.Je., Safonov A.A. Sanacija teplovyh setej metodom cementirovanija // Novosti teplosnabzhenija. 2011. №11 (135). S. 18 – 23.
- O vozmozhnosti primenenija novoj tehnologii pri remontah truboprovodov teplosetej / Fajnshtejn A.V., Musienko L.V., Samsonova L.V., Nekrasova O.G. // Zhurnal mezhdunarodnogo nauchnogo instituta Educatio. 2015. №6 (13) Chast’ 2. S. 12 – 14.
- O metodah NK, primenjaemyh dlja diagnostiki truboprovodov teplovyh setej / L.V. Polenova, N.V. Chernovec, N.V. Ivanov, D.E. Chujko // V mire nerazrushajushhego kontrolja. 2009. №4 (46). S. 25 – 28.
- Pomaskina T.I. Perspektivnyj metod // ZhKH: tehnologii i oborudovanie. 2008. №12. S. 30 – 31.
1.Расчёт потерь давления в магистральном трубопроводе 6
2.Расчёт потерь давления в параллельном трубопроводе 10
3.Расчёт потерь давления и расхода жидкости в разветвлённом трубопроводе 13
3.1Расчёт потерь давления и расхода жидкости в разветвлённом трубопроводе при нормальном режиме 13
3.2 Расчёт потерь давления и расхода жидкости в разветвлённом трубопроводе при аварийном режиме работы 16
Список литературы 20
Расчёт потерь давления в магистральном трубопроводе
Магистральный трубопровод имеет компенсаторы через каждые 100м длины и следующие параметры:
Длина, м | Диаметр, мм | Перепад высот, м | Материал | Качество труб | Компенсаторы |
900 | 616 | 6 | бетон | новые | Лирообразные |
Перепад
давления  ,
необходимый для транспортировки жидкости
на расстояние L,
складывается из перепада, необходимого
для преодоления сопротивления при
стабилизированном движении
,
необходимый для транспортировки жидкости
на расстояние L,
складывается из перепада, необходимого
для преодоления сопротивления при
стабилизированном движении  и местных сопротивлений
и местных сопротивлений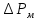 ,
то есть
,
то есть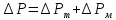 .
.
Потери при стабилизированном движении и местных сопротивлений можно вычислить из формул Дарси-Вейсбаха:
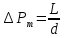 ,
[Па]
,
[Па]
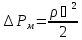 ,
[Па]
,
[Па]
где – гидравлический коэффициент трения;
L– длина трубопровода, м;
 –диаметр
трубопровода, м;
–диаметр
трубопровода, м;
– коэффициент местного сопротивления;
 –плотность
жидкости в трубопроводе,
–плотность
жидкости в трубопроводе,  ;
;
 –скорость
потока жидкости в трубопроводе,
–скорость
потока жидкости в трубопроводе,  .
.
Так как трубопровод круглого сечения, то площадь его сечения можно найти по формуле:
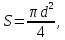 [м2]
[м2]
Полный расход жидкости в трубопроводе выражается формулой:
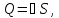 [
[ ]
]
Подставляя
эти формулы в формулы расчёта потерь
давления при
стабилизированном движении  и
местных сопротивлениях
и
местных сопротивлениях  получим:
получим:
 ,
,
 ,
,
Записав полученные выражения в формулу перепада давлений, получим:

Для
упрощения дальнейших записей обозначим 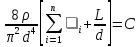 ,
получим
,
получим
Через каждые 100м длины трубопровода установлены лирообразные компенсаторы, которые играют роль местных сопротивлений, т.е. n=8.
Для лирообразного компенсатора коэффициент местного сопротивления равен =2,832.
Температуру
воды в трубопроводе возьмём равной 0 .
Тогда плотность воды равна
.
Тогда плотность воды равна ,
коэффициент вязкости воды равен
,
коэффициент вязкости воды равен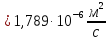
Вычислим
гидравлический коэффициент трения .
Для этого необходимо определить зону
сопротивления, вычислив число Рейнольдса  и определив эквивалентную шероховатость
и определив эквивалентную шероховатость ,
определяемую материалом труб и степенью
их износа. Для новых бетонных труб
,
определяемую материалом труб и степенью
их износа. Для новых бетонных труб .
Число Рейнольдса
.
Число Рейнольдса определяется по формуле:
определяется по формуле:
 ,
,
где  – кинематический коэффициент вязкости,
зависящий от температуры воды,
– кинематический коэффициент вязкости,
зависящий от температуры воды,
Число Рейнольдса, равно:

Следуя
из неравенства  ,
получаем зону квадратичного
сопротивления, для которой коэффициент
трения
находится по формуле Шифринсона:
,
получаем зону квадратичного
сопротивления, для которой коэффициент
трения
находится по формуле Шифринсона:
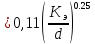
где  – относительная шероховатость.
– относительная шероховатость.
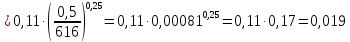
Получим
перепад давления  ,
равный:
,
равный:

Из
уравнения Бернулли выразим разность
статических давлений 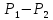 ,
учитывая что скорость потока жидкости
в трубе постоянна
,
учитывая что скорость потока жидкости
в трубе постоянна :
:
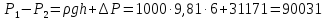 Па
Па
Расчёт потерь давления в параллельном трубопроводе
Падение давления в ветвях параллельного трубопровода обусловлено местными сопротивлениями, включающими:
№ ветви | Диаметр, мм | Задвижка, шт. | Вентиль, шт. | Колено, шт. | Клапан, шт. | Тройник, шт. |
1 | 359 | 4 | 2 | 14 | 3 | 5 |
2 | 404 | 2 | 3 | 12 | 2 | 6 |
3 | 307 | 5 | 4 | 18 | 4 | 3 |
При параллельном соединении трубопроводов все они имеют общие начальную и конечную точки. Уравнение Бернулли для начального и конечного сечения каждого трубопровода будет иметь один и тот же вид:

Следовательно,
потери давления во всех ветвях
параллельного соединения будут одинаковы:  ,
где
,
где
 .
.
Из уравнения неразрывности сумма расходов в ветвях равна полному подводимому расходу:

Решим систему уравнений:
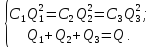
Получим уравнение:
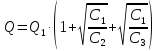
Падение давлений в ветвях происходит на местных сопротивлениях.
Примем следующие коэффициенты местного сопротивления:
Задвижка (простая задвижка на трубе круглого сечения диаметром d):
 , при
, при
Вентиль (с прямым затвором):

Колено (с острыми кромками в месте поворота):
 , при
, при
Клапан (шарнирный клапан):
 , при
, при
Тройник:

Коэффициент местного сопротивления равен:

Получим 1 для первой ветви параллельного трубопровода 1=49,4, для второй ветви – 2=40, а для третьей – 3=65,8.
Рассчитаем С1, С2 и С3.


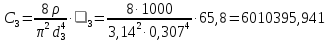
Найдём объёмный расход жидкости в первой ветви трубопровода:

Следовательно, потери давления в параллельном трубопроводе: