формулы и определения / Блог :: Бингоскул

Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.

 

Закон Ома для участка цепи:

Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.

1. I — сила тока (в системе СИ измеряется — Ампер)
   • Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
   • Формула: I=\frac{U}{R}
2. U — напряжение (в системе СИ измеряется — Вольт)
3. R — электрическое сопротивление (в системе СИ измеряется — Ом).
   • Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
   • Формула R=\frac{U}{I}

 

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1 (Ампер).

 

Закон Ома для полной цепи

Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника

 

Формула I=\frac{\varepsilon}{R+r}

• \varepsilon — ЭДС источника напряжения, В;
• I — сила тока в цепи, А;
• R — сопротивление всех внешних элементов цепи, Ом;
• r — внутреннее сопротивление источника напряжения, Ом.

 

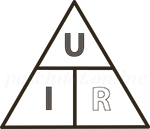
Как запомнить формулы закона Ома

Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.

.

 

• U — электрическое напряжение;
• I — сила тока;
• P — электрическая мощность;
• R — электрическое сопротивление

---

 

Смотри также:

 

Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.

Закон Ома для участка цепи простым языком для чайников

Вся прикладная электротехника базируется на одном догмате — это закон Ома для участка цепи. Без понимания принципа этого закона невозможно приступать к практике, поскольку это приводит к многочисленным ошибкам. Имеет смысл освежить эти знания, в статье мы напомним трактовку закона, составленного Омом, для однородного и неоднородного участка и полной цепи.

Диаграмма, упрощающая запоминание

Классическая формулировка

Этот простой вариант трактовки, известный нам со школы.

Однородный открытый участок электроцепи

Формула в интегральной форме будет иметь следующий вид:

Формула в интегральной форме

То есть, поднимая напряжение, мы тем самым увеличиваем  ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I».  Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.

В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.

Принятые единицы измерения

Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:

• напряжение – в вольтах;
• ток в амперах
• сопротивление в омах.

Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.

Формулировка для полной цепи

Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.

Схема с подключенным с источником

Учитывая «r» ЭДС, формула предстанет в следующем виде:



Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.

Напряжение будет  меньше ЭДС, определить его можно по формуле:



Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.

Неоднородный участок цепи постоянного тока

Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.

Схема неоднородного участка

Формула для такого участка (обобщенный закон) будет иметь следующий вид:

Формула для неоднородного участка цепи

Переменный ток

Если в схема, подключенная к переменному току снабжена емкостью и/или индуктивностью (катушкой), расчет производится с учетом величин их реактивных сопротивлений. Упрощенный вид закона будет выглядеть следующим образом:



Где «Z» представляет  собой импеданс, это комплексная величина, состоящая из активного (R) и пассивного (Х) сопротивлений.

Практическое использование

Видео: Закон Ома для участка цепи — практика расчета цепей.


Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.

Применяем закон к любому участку цепи
Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.
Находим силу тока
Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:
• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

Преобразуем исходные данные:

• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление.

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.

Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров.

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Вывод

Как уже упоминалось в начале статьи, вся прикладная электротехника базируется на законе, составленном Омом. Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.

Подготовка электриков как специалистов начинается с изучения теоретических основ электротехники. И первое, что они должны запомнить – это закон составленный Омом, поскольку на его основе производятся практически все расчеты параметров электрических цепей различного назначения.

Понимание основного закона электротехники поможет лучше разбираться в работе электрооборудования и его основных компонентов. Это положительно отразится на техническом обслуживании в процессе эксплуатации.

Самостоятельная проверка, разработка, а также опытное изучение узлов оборудования – все это существенно упрощается, если использовать закон Ома для участка цепи. При этом не требуется проводить всех измерений, достаточно снять некоторые параметры и, проведя несложные расчеты, получить необходимые значения.

Закон Ома для участка цепи и полной цепи: формулы и объяснение

Для электрика и электронщика одним из основных законов является Закон Ома. Каждый день работа ставит перед специалистом новые задачи, и зачастую нужно подобрать замену сгоревшему резистору или группе элементов. Электрику часто приходится менять кабеля, чтобы выбрать правильный нужно «прикинуть» ток в нагрузке, так приходится использовать простейшие физические законы и соотношения в повседневной жизни. Значение Закона Ома в электротехники колоссально, к слову большинство дипломных работ электротехнических специальностей рассчитываются на 70-90% по одной формуле.

Историческая справка

Год открытия Закон Ома  — 1826 немецким ученым Георгом Омом. Он эмпирически определил и описал закон о соотношении силы тока, напряжения и типа проводника. Позже выяснилось, что третья составляющая – это не что иное, как сопротивление. Впоследствии этот закон назвали в честь открывателя, но законом дело не ограничилось, его фамилией и назвали физическую величину, как дань уважения его работам.

Величина, в которой измеряют сопротивление, названа в честь Георга Ома. Например, резисторы имеют две основные характеристики: мощность в ваттах и сопротивление – единица измерения в Омах, килоомах, мегаомах и т.д.

Закон Ома для участка цепи

Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:

I=U/R

Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.

Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.

Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже.

Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:

f(x) = ky или f(u) = IR или f(u)=(1/R)*I

Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:

I=12 В/6 Ом=2 А

Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.

Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.



Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:

R_провод=ρ(L/S)

Где ρ – удельное сопротивление в Ом*мм²/м, L – длина в м, S – площадь поперечного сечения.

Закон Ома для параллельной и последовательной цепи

В зависимости от типа соединения наблюдается разный характер протекания тока и распределения напряжений. Для участка цепи последовательного соединения элементов напряжение, ток и сопротивление находятся по формуле:

I=I1=I2

U=U1+U2

R=R1+R2

Это значит, что в цепи из произвольного количества последовательно соединенных элементов протекает один и тот же ток. При этом напряжение, приложенное ко всем элементам (сумма падений напряжения), равно выходному напряжению источника питания. К каждому элементу в отдельности приложена своя величина напряжений и зависит от силы тока и сопротивления конкретного:

U_эл=I*R_{элемента}

Сопротивление участка цепи для параллельно соединённых элементов рассчитывается по формуле:

I=I1+I2

U=U1=U2

1/R=1/R1+1/R2

Для смешанного соединения нужно приводить цепь к эквивалентному виду. Например, если один резистор соединен с двумя параллельно соединенными резисторами – то сперва посчитайте сопротивление параллельно соединенных. Вы получите общее сопротивление двух резисторов и вам остаётся сложить его с третьим, который с ними соединен последовательно.



Закон Ома для полной цепи

Полная цепь предполагает наличие источника питания. Идеальный источник питания – это прибор, который имеет единственную характеристику:

• напряжение, если это источник ЭДС;
• силу тока, если это источник тока;

Такой источник питания способен выдать любую мощность при неизменных выходных параметрах. В реальном же источнике питания есть еще и такие параметры как мощность и внутреннее сопротивление. По сути, внутреннее сопротивление – это мнимый резистор, установленный последовательно с источником ЭДС.



Формула Закона Ома для полной цепи выглядит похоже, но добавляется внутренне сопротивление ИП. Для полной цепи записывается формулой:

I=ε/(R+r)

Где ε – ЭДС в Вольтах, R – сопротивление нагрузки, r – внутреннее сопротивление источника питания.

На практике внутреннее сопротивление является долями Ома, а для гальванических источников оно существенно возрастает. Вы это наблюдали, когда на двух батарейках (новой и севшей) одинаковое напряжение, но одна выдает нужный ток и работает исправно, а вторая не работает, т.к. проседает при малейшей нагрузке.

Закон Ома в дифференциальной и интегральной форме

Для однородного участка цепи приведенные выше формулы справедливы, для неоднородного проводника необходимо его разбить на максимально короткие отрезки, чтобы изменения его размеров были минимизированы в пределах этого отрезка. Это называется Закон Ома в дифференциальной форме.



Иначе говоря: плотность тока прямо пропорциональной напряжённости и удельной проводимости для бесконечно малого участка проводника.



В интегральной форме:



Закон Ома для переменного тока

При расчете цепей переменного тока вместо понятия сопротивления вводят понятие «импеданс». Импеданс обозначают буквой Z, в него входит активное сопротивление нагрузки R_a и реактивное сопротивление X (или R_r). Это связано с формой синусоидального тока (и токов любых других форм) и параметрами индуктивных элементов, а также законов коммутации:

1. Ток в цепи с индуктивностью не может измениться мгновенно.
2. Напряжение в цепи с ёмкостью не может измениться мгновенно.

Таким образом, ток начинает отставать или опережать напряжение, и полная мощность разделяется на активную и реактивную.

U=I*Z



X_L и X_C – это реактивные составляющие нагрузки.

В связи с этим вводится величина cosФ:



Здесь – Q – реактивная мощность, обусловленная переменным током и индуктивно-емкостными составляющими, P – активная мощность (выделяется на активных составляющих), S – полная мощность, cosФ – коэффициент мощности.

Возможно, вы заметили, что формула и её представление пересекается с теоремой Пифагора. Это действительно так и угол Ф зависит от того, насколько велика реактивная составляющая нагрузки – чем её больше, тем он больше. На практике это приводит к тому, что реально протекающий в сети ток больше чем тот, что учитывается бытовым счетчиком, предприятия же платят за полную мощность.

При этом сопротивление представляют в комплексной форме:



Здесь j – это мнимая единица, что характерно для комплексного вида уравнений. Реже обозначается как i, но в электротехнике также обозначается и действующее значение переменного тока, поэтому, чтобы не путаться, лучше использовать j.

Мнимая единица равняется √-1. Логично, что нет такого числа при возведении в квадрат, которого может получиться отрицательный результат «-1».

Как запомнить закон Ома

Чтобы запомнить Закон Ома – можно заучить формулировку простыми словами типа:

Чем больше напряжение – тем больше ток, чем больше сопротивление – тем меньше ток.

Или воспользоваться мнемоническими картинками и правилами. Первая это представление закона Ома в виде пирамиды – кратко и понятно.



Мнемоническое правило – это упрощенный вид какого-либо понятия, для простого и легкого его понимания и изучения. Может быть либо в словесной форме, либо в графической. Чтобы правильно найти нужную формулу – закройте пальцем искомую величину и получите ответ в виде произведения или частного. Вот как это работает:



Вторая – это карикатурное представление. Здесь показано: чем больше старается Ом, тем труднее проходит Ампер, а чем больше Вольт – тем легче проходит Ампер.



Напоследок рекомендуем просмотреть полезное видео, в котором простыми словами объясняется Закон Ома и его применение:

Закон Ома – один из основополагающих в электротехнике, без его знания невозможна бОльшая часть расчетов. И в повседневной работе часто приходится переводить амперы в киловатты или по сопротивлению определять ток. Совершенно не обязательно понимать его вывод и происхождение всех величин – но конечные формулы обязательны к освоению. В заключении хочется отметить, что есть старая шуточная пословица у электриков: «Не знаешь Ома – сиди дома». И если в каждой шутке есть доля правды, то здесь эта доля правды – 100%. Изучайте теоретические основы, если хотите стать профессионалом на практике, а в этом вам помогут другие статьи из нашего сайта.

Закон Ома для участка цепи, пример расчета.

21 Января 2017

1950

Всем привет.
В предыдущей статье мы собрали простую замкнутую цепь, состоящий из источника питания, проводников по которым протекает ток и нагрузки. Выяснили, что такое сопротивление проводника и сопротивление нагрузки. Так же рассмотрели взаимосвязь между напряжением тока, силой тока и сопротивлением на разных участках цепи (проводника и нагрузки). Все эти отношения установлены в основном законе электротехники – в законе Ома.
В этой статье, мы рассмотрим Закон Ома для участка цепи.

Закон Ома для участка цепи

Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи.

Давайте рассмотрим этот закон на примере. Соберем следующую схему:



Так как сопротивление проводников близко к нулю, будем считать, что они равны нулю. В нашу электрическую цепь, кроме нагрузки, мы еще добавили два прибора.
Амперметр – прибор для измерения силы тока, или другими словами измеряет сколько потребляет нагрузка, так легче запомнить. Соединяется последовательно с нагрузкой.
Вольтметр – прибор для измерения напряжения тока, при подключении к нагрузке, показывает сколько падает напряжение на нагрузку. Соединятся параллельно с нагрузкой.

Давайте нагрузку поставим сопротивлением равной 100 Ом, с источника питания пустим напряжение 5 В (вольт). Снимем показания с приборов. Нас интересует показатель амперметра. Амперметр показывает — 0,05 А (ампер) для удобства можно перевести в миллиамперы – 50 мА (миллиампер).



наведите или кликните мышкой, для анимации

Теперь поменяем напряжение тока, вместо 5 В установим 10 В. Снимем показатель амперметра. Амперметр показывает — 0,1 А переводим в миллиамперы – 100 мА. Сразу отметим для себя — с увеличением напряжения увеличилась сила тока.
В законе ома: «сила тока в участке цепи прямо пропорциональна напряжению … ».



наведите или кликните мышкой, для анимации

Теперь вернемся к первому опыту, то есть установим напряжение обратно на значение 5 В. Попробуем изменить сопротивление нагрузки. Поменяем нагрузку со значение сопротивления 200 Ом. Снимем показатели с амперметра и сравним с показателями первого опыта. Амперметр показывает — 0,025 А переводим в миллиамперы – 25 мА. Таким образом увеличение сопротивления нагрузки, уменьшило силу тока.
В законе ома: «сила тока в участке цепи … обратно пропорциональна электрическому сопротивлению».



наведите или кликните мышкой, для анимации

Закон Ома для участка цепи записывается следующей формулой: I = U/R
Как нам уже известно:
I = сила тока
U = напряжение тока
R = сопротивление (сопротивление нагрузки)




Так же эту формулу можно преобразовывать для определения напряжения тока или сопротивления нагрузки. Что бы легче запомнить формулы, надо запомнить треугольник Ома, который изображен выше. Закрывая искомую величину пальцем, можно увидеть формулу для нее.

Формула для определения напряжения:



Формула для определения сопротивления:



Рассмотрим простой пример расчета используя закон Ома для участка цепи. Если в примере выше, мы бы не использовали амперметр, зная напряжение тока 5 В (U) и сопротивление нагрузки 100 Ом (R). Использую следующую формулу I = U/R, мы бы получили результат: 5/100 = 0,05. Ответ 0,05 А = 50 мА.

Мы разобрали закон Ома для участка цепи, ознакомились с формулами для определения силы тока, напряжение тока и сопротивления. Так же хочу добавить, при расчетах, необходимо переводить единицы измерения в систему СИ. В примерах выше для демонстраций замкнутой цепи, я использовал программу — Electronics Workbench. Программа предназначена для моделирования и анализа электронных схем.

Закон Ома — онлайн калькулятор

Чтобы посчитать Закон Ома воспользуйтесь нашим очень удобным онлайн калькулятором:

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Онлайн калькулятор

Найти силу тока



Формула

I = ^U/_R

Пример

Если напряжение на концах участка цепи U = 12 В, а его электрическое сопротивление R = 2 Ом, то:

Сила тока на этом участке I = ¹²/₂= 6 А

Найти напряжение



Формула

U = I ⋅ R

Пример

Если сила тока на участке цепи I = 6 А, а электрическое сопротивление этого участка R = 2 Ом, то:

Напряжение на этом участке U = 6⋅2 = 12 В

Найти сопротивление



Формула

R = ^U/_I

Пример

Если напряжение на концах участка цепи U = 12 В, а сила тока на участке цепи I = 6 А, то:

Электрическое сопротивление на этом участке R = ¹²/₆ = 2 Ом

Закон Ома для полной цепи

Закон Ома для полной цепи гласит, что сила тока в цепи пропорциональна действующей в цепи электродвижущей силе (ЭДС) и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Онлайн калькулятор

Найти силу тока

Формула

I = ^ε/_R+r

Пример

Если ЭДС источника напряжения ε = 12 В, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

Сила тока I = ¹²/₄₊₂ = 2 А

Найти ЭДС

Формула

ε = I ⋅ (R+r)

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а внутреннее сопротивление источника напряжения r = 2 Ом, то:

ЭДС ε = 2 ⋅ (4+2) = 12 В

Найти внутреннее сопротивление источника напряжения

Формула

r = ^ε/_I— R

Пример

Если сила тока в цепи I = 2A, сопротивление всех внешних элементов цепи R = 4 Ом, а ЭДС источника напряжения ε = 12 В, то:

Внутреннее сопротивление источника напряжения r = 12/2 — 4 = 2 Ом

Найти сопротивление всех внешних элементов цепи

Формула

R = ^ε/_I— r

Пример

Если сила тока в цепи I = 2A, внутреннее сопротивление источника напряжения r = 2 Ом, а ЭДС источника напряжения ε = 12 В, то:

Сопротивление всех внешних элементов цепи: R = 12/2 — 2 = 4 Ом

См. также

Закон Ома | Закон Ома для участка цепи, формула

Как говорится в среде радиолюбителей: “Если не знаешь закон Ома, то сиди-ка лучше дома”.

Закон Ома с точки зрения гидравлики

Как вы уже знаете, электрический ток имеет аналогию с гидравликой. Напряжение – это уровень воды в башне. Сопротивление – это  труба или шланг. Сила тока – это объем воды за какой-то период времени.

Теперь давайте рассмотрим такой случай. Пусть вместо башни у нас будет сосуд с водой, в котором пробиты три одинаковых отверстия на разной высоте сосуда. Так как сосуд у нас наполнен водой, следовательно, на дне сосуда давление будет больше, чем на  его поверхности.



Как вы видите, нижняя струя, которая находится ближе ко дну, стреляет дальше, чем средняя струя. А средняя струя стреляет дальше, чем верхняя.  Заметьте, что отверстия у нас везде  одинакового диаметра. То есть можно сказать, что сопротивление каждого отверстия воде одинаково. За одинаковое время, объем воды, вытекаемый с самого нижнего отверстия намного больше, чем объем воды, вытекаемый со среднего и самого верхнего отверстия. А что у нас такое объем воды  за какое-то время? Да это же сила тока!

Итак, какую закономерность мы тут видим? Учитывая, что сопротивление везде одинаковое, получается что с увеличением напряжения увеличивается и сила тока!

Опыт №1

Думаю, у каждого из вас есть садовый участок. Где-то недалеко от вас всегда есть водонапорная башня



Для чего нужна водонапорная башня? Для контроля уровня расхода воды, а также для создания давления в трубах, иначе как вы  будете поливать свои огурцы? Вы никогда  не замечали, что башню возводят  где-нибудь на возвышенности? Для чего это делается? Как раз для того, чтобы создать давление.

Предположим, что ваш садовый участок находится выше, чем верхушка водобашни. Что произойдет в этом случае? Вода просто-напросто не дойдет до вас! Физика… закон сообщающихся сосудов.

У всех на кухне и в ванной есть краник. После очередного трудового дня вы решили помыть руки. Для этого вы на полную катушку включаете воду, и она начинает течь бурным потоком из краника:



Но вас не устраивает такой поток воды, поэтому, покрутив ручку крана, вы уменьшаете поток воды на минимум:



Что только что сейчас произошло?

Поменяв сопротивление потоку с помощью ручки краника, вы добились того, что этот поток воды стал течь очень слабо.

Давайте же проведем аналогию этой ситуации с электрическим током. Итак, что имеем? Напряжение потока мы не меняли. Где-то там вдалеке стоит водобашня и создает давление в трубах. Мы ведь не имеем права трогать водобашню, а тем более ее сносить). Поэтому уровень воды в башне все время полный, так как насос все время подкачивает воду до максимального уровня. Следовательно, напряжение у нас постоянное и не меняется.

Закрутив обратно ручку краника, мы  только что поменяли сопротивление трубы, из которой сделан краник. В данном случае мы увеличили сопротивление потоку воды. А что у нас получилось с потоком водички? Она стала бежать медленнее! То есть, можно сказать, что количество молекул воды за какое-то время при полностью открытом и полузакрытом кранике получилось разное. Ну-ка, вспоминаем, что такое сила тока 😉 Кто забыл, напомню – это количество электронов протекающих через поперечное сечение проводника за какой-то период времени. И что у нас стало с этой силой тока? Она уменьшилась!

Делаем вывод:

При увеличении сопротивления, сила тока, проходящая через это сопротивление, уменьшается.


Опыт N2

Итак. Имеем вот такую схему водоснабжения:



Теперь представьте, что вы поливаете огород и вам  надо наполнить  бочку с водой из шланга за 10 минут. Ни секундой раньше и не позже! У вас в огороде поток воды бежит примерно вот так:



Допустим, с водобашни у нас идет простой резиновый шланг. Сосед случайно припарковал свой автомобиль прямо на шланге и чуть-чуть придавил его



У вас поток воды стал убывать. Идти ругаться с соседом? Он уже ушел по делам, а бочку за 10 минут  наполнить не успеете. Потребуется больше времени. Как же быть? А почему бы нам не открыть краник перед водобашней чуток побольше? А это хорошая идея! Открываем краник на полную катушку и добиваемся, чтобы уровень воды в башне стал еще больше, чем был до этого (хотя  в башнях стоят защиты от переполнения какого-либо максимального уровня, но для примера упустим этот момент).

Итак, что у нас получается? Сосед придавил шланг, значит увеличил сопротивление. Поэтому сила тока у нас стала меньше. Чтобы восстановить силу тока, мы для этого увеличивали напряжение, то есть уровень воды в башне.

Вывод: при увеличении напряжения увеличивается и сила тока.

Опыт №3

Но беда не приходит одна. На башне сломалось реле контроля водонасоса! Насос качает воду и не отключается! Башня переполняется и поток воды из шланга с каждой секундой становиться все больше и больше! Что же делать? Мы же переполним нашу бочку за отведенное нам время! Спокойствие, только спокойствие… Выход есть! Для этого бежим и чуток перекрываем краник , добиваясь того, чтобы поток воды из шланга тек также, как и раньше 😉

В этом случае уровень воды (напряжение) на водобашне стал увеличиваться из-за того, что насос не отключался и все время качал воду. Поэтому, поток воды (сила тока) у нас тоже стала  расти. Чтобы выровнять силу тока, мы увеличили сопротивление краника ;-), тем самым привели в норму уровень воды в водобашне (напряжение) до приемлемого уровня.


Формула Закона Ома

Ну как, увидели закономерность из всего вышеописанного? А вот немецкий физик Георг Ом с помощью простых опытов нашел все-таки связь между этими тремя величинами и с тех пор этот закон носит его имя:




где

I – это сила тока, выражается в Амперах (А)

U – напряжение, выражается в Вольтах (В)

R – сопротивление, выражается в Омах (Ом)

Заключение

Закон Ома является самым главным законом в электронике. Абсолютно вся теория цепей построена именно на законе Ома. Поэтому, чтобы научиться читать электрические схемы, вам очень важно знать, как связаны напряжение, сила тока и сопротивление на участке цепи. В этой статье мы с вами разобрали закон Ома для участка цепи, но есть еще закон Ома для полной цепи, о котором можно прочитать в этой статье.

Более подробно про закон Ома для участка цепи вы можете также прочитать в этой статье.

Электротехника. Основы. Закон Ома — Всё об энергетике

Электротехника. Основы. Закон Ома

В электротехнике, как и в любой другой науке, существуют базовые понятия, без понимания которых не удастся овладеть этой областью знаний. Здесь такими понятиями являются электрическое напряжение, электрический ток и электрическое сопротивление.

Закон Ома

Закон Ома был открыт в результате экспериментов Георга Ома с гальванометром и простой электрической цепью из источника ЭДС и сопротивления. Со временем формула полученная Омом претерпела несколько изменений.

Закон Ома для участка цепи без ЭДС

Может быть сформулирован через сопротивление [1, стр.33][2, стр.15]:

\begin{equation} I = {U_{ab}\over R}; \end{equation}

Где:

• I — ток через участок ab электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = U_{ab} × G; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (1, 2) справедлива для электрической цепи представленной ниже на рисунке 1.



Рисунок 1 — Участок цепи без ЭДС

Закон Ома для участка цепи содержащего ЭДС

Или обобщённый закон Ома. Формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {U_{ab} + E\over R}; \end{equation}

Где:

• I — ток через участок ac электрической цепи;
• U_ab — напряжение на участке ab электрической цепи;
• E — ЭДС на участке bс электрической цепи;
• R — сопротивление участка ab электрической цепи.

Или через проводимость:

\begin{equation} I = {(U_{ab} + E) × G}; \end{equation}

Где:

• G — проводимость участка ab электрической цепи.

Формула (3, 4) справедлива для электрической цепи представленной ниже на рисунке 2.



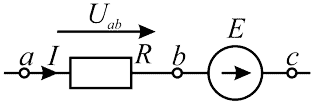
Рисунок 2 — Участок цепи содержащий ЭДС

Закон Ома для полной цепи

Закон формулируется следующим образом [1, стр.34][2, стр.17]:

\begin{equation} I = {E\over {R + r}}; \end{equation}

Где:

• I — ток в электрической цепи;
• E — ЭДС электрической цепи;
• R — сопротивление электрической цепи;
• r — внутреннее сопротивление источника ЭДС.

Формулировка выражения (5) через проводимость неудобна и здесь приведена не будет. Ниже на рисунке 3 изображена схема электрической цепи для которой справедливо выражение (5).



Рисунок 3 — Полная цепь

На схеме видно, что R и r соединены последовательно, а в формуле это отражено как сумма R (сопротивления цепи) и r (внутреннего сопротивления источника ЭДС). Заменим выражение R + r на R_п

\begin{equation} I = {E\over R_п}; \end{equation}

Где:

• R_п — полное сопротивление электрической цепи (включая сопротивление источника ЭДС).

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме, представленный в выражении (7), справедлив для неоднородного, но изотропного вещества [3].

\begin{equation} \vec E = {ρ × \vec\jmath}; \end{equation}

Где:

• \(\vec\jmath\) — плотность тока;
• ρ — удельное сопротивление;
• \(\vec E\) — напряжённость электрического поля.

Примеры применения

Ниже приведены несколько примеров для демонстрации применения разных формулировок закона Ома.

Пример 1

Схема задания приведена на рисунке 4. На схеме R = 5,2 Ом, U = 26 В. Определить I.



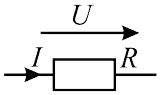
Рисунок 4 — Схема к 1 и 2-му примеру

Для решения задания воспользуемся выражением (1):

\begin{equation} I = {U\over R} = {26\over 5,2} = {5 \ А;} \end{equation}

Пример 2

Схема задания приведена на рисунке 4. К данному участку цепи приложено напряжение 24 В и по нему протекает ток 1,5 А. Определить проводимость участка цепи.

Для решения задания преобразуем выражение (2) относительно G:

\begin{equation} I = {U × G} \ \Rightarrow \ G = {I\over U} = {1,5\over 24} = {0,0625 \ См;} \end{equation}

Пример 3

Схема задания приведена на рисунке 5. На схеме U = 220 В, I = 0,5 А, R = 140 Ом. Определить E.



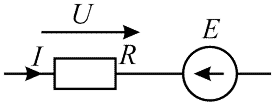
Рисунок 5 — Схема к 3-му примеру

Для решения задания преобразуем выражение (3) относительно E:

\begin{equation} I = {U — E\over R} \ \Rightarrow \ {I × R} = {U — E} \ \Rightarrow \ E = {U — I × R}; \end{equation}

Подставим в выражение (10) известные величины:

\begin{equation} E = {U — I × R} = {220 — 0,5 × 140} = {150 \ В;} \end{equation}

Пример 4

Сопротивление электрической цепи, приведенной на рисунке 3 составляет 12 Ом, напряжение источника ЭДС включенного в цепь — 9 В. Измерения показали, что по цепи протекает ток 0,72 А. Необходимо определить внутреннее сопротивление источника ЭДС.

Преобразуем выражение (5) относительно r:

\begin{equation} I = {E\over {R + r}} \ \Rightarrow \ {I × (R + r)} = E \ \Rightarrow \ {I × r} = {E — I × R} \ \Rightarrow \ r = {E — I × R\over I}; \end{equation}

Определим внутренней сопротивление источника ЭДС, подставив в выражение (10) известные величины:

\begin{equation} r = {E — I × R\over I} = {9 — 0,72 × 12\over 0,72} = {0,36\over 0,72} = {0,5 \ Ом;} \end{equation}

Использованные термины

Электрический потенциал точки:

Физическая величина, равная потенциальной энергии, которой обладает элементарный положительный заряд, помещенный в электрическое поле.

Потенциал обозначается буквой φ греческого алфавита и измеряется в вольтах (В). Он не имеет направления и записывается как скаляр.

Электрическое напряжение:

Физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из точки А в точку Б электромагнитного поля, определяемая как разность потенциалов этих точек: U_ab = φ_a — φ_b.

Напряжение обозначается буквой U (u) латинского алфавита и измеряется в вольтах (В). Напряжение — скалярная величина, но на электрических схемах указывают его положительное направление.

Электродвижущая сила (ЭДС):

Также как и напряжение это физическая величина, равная количеству энергии, затраченной на перенос единичного заряда из одной точки электромагнитного поля в другую.

ЭДС обозначается буквой E (e) латинского алфавита и измеряется в вольтах (В). ЭДС — скалярная величина, но на электрических схемах указывают её положительное направление. Она численно равна напряжению на зажимах не подключенного источника.

Электрическое ток:

Физическая величина, равная количеству заряженных частиц прошедших через поперечное сечение проводника за единицу времени. Как явление — направленное движение заряженных частиц.

Напряжение обозначается буквой I (i) латинского алфавита и измеряется в амперах (А). Ток, так же как и напряжение, величина скалярная, и на электрических схемах тоже указывают его положительное направление [2, стр.11].

Плотность тока:

Физическая величина, имеющая смысл силы электрического тока, протекающего через элемент поверхности единичной площади.

Плотность тока обозначается буквой \(\vec\jmath\) латинского алфавита и измеряется в амперах на метр квадратный (А/м²). Плотность тока — векторная величина [4].

Электрическое сопротивление:

Физическая величина, характеризующая способность проводника препятствовать прохождению по нему тока.

Сопротивление обозначается буквами R (r), X (x) или Z (z) латинского алфавита (последние два обозначения применяются для реактивного и комплексного сопротивления соответственно) и измеряется в омах (Ом). Как и предыдущие, сопротивление — скалярная величина.

Электрическая проводимость:

Физическая величина, характеризующая насколько хорошо проводник проводит электрический ток, является обратной сопротивлению: G = 1/R.

Проводимость обозначается буквами G (g) латинского алфавита и измеряется в сименсах (См). Так же как и сопротивление проводимость — скалярная величина.

Удельное сопротивление:

Физическая величина, численно равная сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м².

Удельная проводимость обозначается буквами ρ греческого алфавита и измеряется в омах на метр (Ом×м). Является скалярной величиной. [3].

В дальнейшем при использовании вышеперечисленных терминов слово «электрический» будет упускаться.

Список использованных источников

1. Бессонов, Л.А. Теоретические основы электротехники: учебник / Л.А. Бессонов — Москва: Высшая школа, 1996. — 623 с.
2. Иванова, С.Г. Теоретические основы электротехники: Версия 1.0 [Электронный ресурс] : учеб. пособие / С. Г. Иванова, В. В. Новиков – Красноярск: ИПК СФУ, 2008. — 318 с.
3. Википедия — Удельное электрическое сопротивление [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Удельное_электрическое_сопротивление
4. Википедия — Плотность тока [электронный ресурс] — Режим доступа: https://ru.wikipedia.org/wiki/Плотность_тока