elektrotekhnika_pervaya_laba_zaschita
Какие электрические цепи называются линейными?
Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и индуктивности.
Сформулируйте законы Кирхгофа. Что отражают они физически?
Первое правило Кирхгофа (правило токов Кирхгофа) гласит, что алгебраическая сумма токов в каждом узле любой цепи равна нулю. При этом втекающий в узел ток принято считать положительным, а вытекающий — отрицательным:
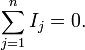
Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма падений напряжений на всех ветвях, принадлежащих любому замкнутому контуру цепи, равна алгебраической сумме ЭДС ветвей этого контура. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:
Физический смысл второго закона Кирхгофа
Второй закон устанавливает связь между падением напряжения на замкнутом участке электрической цепи и действием источников ЭДС на этом же замкнутом участке. Он связан с понятием работы по переносу электрического заряда. Если перемещение заряда выполняется по замкнутому контуру, возвращаясь в ту же точку, то совершенная работа равна нулю. Иначе бы не выполнялся закон сохранения энергии. Это важное свойство потенциального электрического поля описывает 2 закон Кирхгофа для электрической цепи.
Физический смысл первого закона Кирхгофа
Первый закон устанавливает связь между токами для узлов электрической цепи. Он вытекает из принципа непрерывности, согласно которому суммарный поток зарядов, образующих электрический ток, проходящих через любую поверхность равен нулю. Т.е. количество прошедших зарядов в одну сторону равно количеству зарядов, прошедших в другую сторону. Т.е. количество зарядов никуда не может деться. Они не могу прост исчезнуть.
сколько уравнений составляется по первому закону Кирхгофа и сколько по второму?
Кол-во уравнений, первый закон Кирхгофа = Кол-во узлов – 1
Кол-во уравнений, второй закон Кирхгофа = Кол-во ветвей – Кол-во узлов + 1
Понятие независимого контура. Чему равно число независимых контуров в любой цепи?
Независимый контур — это замкнутый участок электрической цепи, проложенный через ветви цепи, содержащий хотя бы одну новую ветвь, неиспользованную при поиске других независимых контуров.
понятия узел, ветвь, электрическая цепь.
Электрическая цепь характеризуется совокупностью элементов, из которых она состоит, и способом их соединения. Соединение элементов электрической цепи наглядно отображается ее схемой. Рассмотрим для примера две электрические схемы (рис. 1, 2), введя понятие ветви и узла.
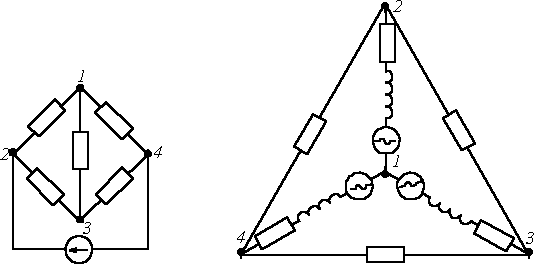
Ветвью называется участок цепи, обтекаемый одним и тем же током.
Узел – место соединения трех и более ветвей.
Что такое потенциальная диаграмма как она строится?
Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат — потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
Каковы особенности режимов работы аккумуляторной батареи?
Метод наложения его достоинства и недостатки
Сущность метода эквивалентного генератора и способы определения параметров активного двухполюсника
Этот
метод применяется в тех случаях, когда
требуется рассчитать ток в какой-либо
одной ветви при нескольких значениях
ее параметров (сопротивления и ЭДС) и
неизменных параметрах всей остальной
цепи. Сущность метода заключается в
следующем. Вся цепь относительно зажимов
интересующей нас ветви представляется
как активный двухполюсник, который
заменяется эквивалентным генератором,
к зажимам которого подключается
интересующая нас ветвь. В итоге получается
простая неразветвленная цепь, ток в
которой определяется по закону Ома. ЭДС
Е
Сущность метода контурных токов и напряжения двух узлов.
Метод контурных токов можно применить для расчета сложных электрических цепей, имеющих больше двух узловых точек. Сущность метода контурных токов заключается в предположении, что в каждом контуре проходит свой ток (контурный ток). Тогда на общих участках, расположенных на границе двух соседних контуров, будет протекать ток, равный алгебраической сумме токов этих контуров.
Режимы работы источников питания.
Покажите, что условием максимальной передачи мощности от источника к приемнику электрической энергии является равенство Rвн=Rн
Электрическая цепь Википедия
| Электрическая цепь | |
Условное обозначение электрической цепи | |
| Изучается в | Теория электрических цепей[d] |
|---|---|
| Альтернативное имя | гальваническая цепь |
 Медиафайлы на Викискладе Медиафайлы на Викискладе | |
Электри́ческая цепь (гальвани́ческая цепь) — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.
Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).
Классификация электрических цепей[ | ]
Неразветвленные и разветвленные электрические цепи[ | ]
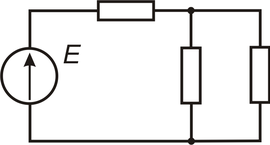
Электрические цепи подразделяют на неразветвленные и разветвленные. Во всех её элементах неразветвленной цепи течёт один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 1. В ней имеются три ветви и два узла. В каждой ветви течёт свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течёт одинаковый ток) и заключённый между двумя узлами. В свою очередь, узел есть точка цепи, в которой сходятся не менее трёх ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 1), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом.
Линейные и нелинейные электрические цепи[ | ]
Линейной электрической цепью называют такую цепь, все компоненты которой линейные. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсато
1. Нелинейная электрическая цепь. Основные понятия
ЛЕКЦИЯ № 15
НЕЛИНЕЙНЫЕ РЕЗИСТИВНЫЕ ЭЛЕМЕНТЫ И ИХ ХАРАКТЕРИСТИКИ
Учебные вопросы
1. Нелинейная электрическая цепь. Основные понятия и определения.
2. Классификация нелинейных элементов и их характеристики.
3. Статические и дифференциальные параметры резистивных линейных элементов.
В электротехнике, автоматике, электронике и радиотехнике широко применяются элементы электрических цепей, имеющие нелинейную зависимость между током и напряжением:
u = f(i) или
Нелинейным элементом называется элемент, параметр которого существенно зависит от приложенного напряжения или от проходящего по нему тока.
В зависимости от типа параметра различают нелинейные резистивные, индуктивные и емкостные элементы, которые имеют соответственно нелинейные сопротивления R(I) или R(U), нелинейные индуктивности L(I) или L(U), нелинейные емкости C(I) или C(U).
Нелинейные элементы описываются нелинейными уравнениями или соответствующими нелинейными вольтамперными i(u) (рис.15.1,а), вебер-амперными (i) (рис.29.1,б) и кулон-вольтными q(u) (рис.15.1,в) характеристиками.
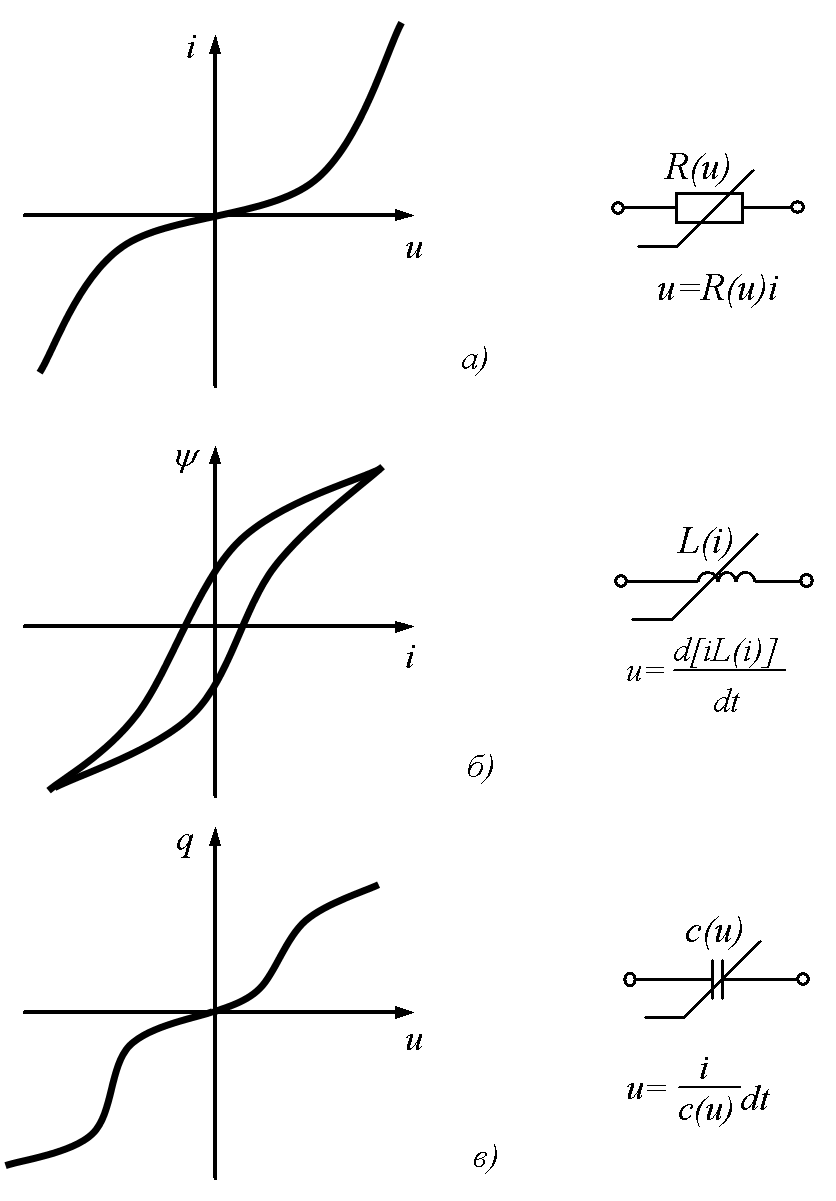
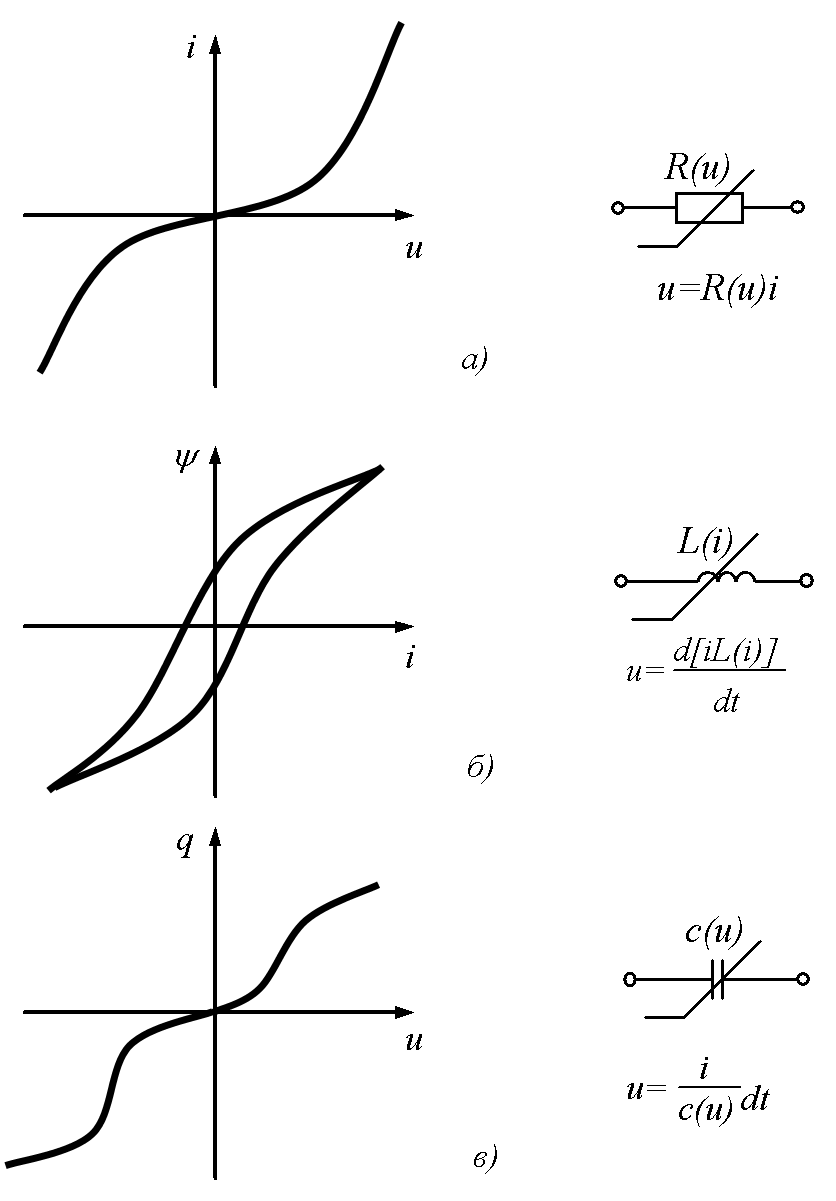
Рис. 15.1
Электрическая цепь, которая содержит хотя бы один нелинейный элемент называется нелинейной.
В нелинейных цепях не соблюдается принцип наложения. Это свойство нелинейных цепей связано с природой характеристик нелинейных элементов, нарушающий пропорциональность между током и напряжением, поэтому не существует общего метода анализа нелинейных цепей. Это является причиной трудности их анализа.
Нелинейность электрических цепей почти всегда приводит к существенно новым явлениям, которые принципиально не могут возникнуть в линейных цепях.
Эти явления обусловливают следующие преобразовательные свойства нелинейных цепей, имеющие большое практическое значение в электротехнике и радиоэлектронике:
1) преобразование частотного состава (спектра) входного сигнала, т.е. при гармоническом входном сигнале выходной сигнал нелинейной цепи является негармоническим и может содержать высшие гармоники и постоянную составляющую;
2) изменение формы входного сигнала, приводящее к изменению его спектра и наоборот;
3) выпрямление переменного напряжения (тока), осуществляемое с помощью нелинейных элементов с односторонней проводимостью;
4) автоколебания, т.е. незатухающие колебания, частота и амплитуда которых не зависит от входного сигнала, а зависит от параметров нелинейной цепи;
5) релейный или триггерный эффект – скачкообразное изменение выходной величины при плавном изменении входной.
Если оценивать строго, то все электрические цепи нелинейны, поскольку характеристики всех реальных элементов в той или иной степени нелинейны. В одних случаях нелинейность характеристик невелика и при построении упрощенной модели ею можно пренебречь, в других нелинейностью характеристик реальных элементов пренебречь нельзя.
Нелинейность характеристик реальных элементов обычно считается несущественной, если ее наличие не является принципиальным для функционирования устройства, а ее влияние приводит лишь к появлению некоторых второстепенных эффектов, которыми в рамках решаемой задачи можно пренебречь.
На практике нелинейностью характеристик реального элемента, как правило, можно пренебречь, если характеристика элемента практически линейна в рабочем диапазоне токов и напряжений, а функционирование устройства не построено на использовании нелинейности соответствующей характеристики.
Рассмотрим основные особенности и методы расчета цепей, содержащих нелинейные резистивные элементы (нелинейные резисторы, транзисторы, диоды и т.д.), наиболее часто применяемые в электропреобразовательной технике и электронике.
Нелинейные емкостные элементы применяются чаще всего в радиоэлектронике и в настоящем курсе не рассматриваются. Нелинейные индуктивные элементы будут рассмотрены в Разделе 3 настоящей дисциплины.
Основные понятия и законы теории электрических цепей
33
Электрическая цепь и ее элементы
Реальной электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и преобразования энергии. В общем случае электрическая цепь содержит источники электрической энергии, приемники электрической энергии, измерительные приборы, коммутационную аппаратуру, соединительные линии и провода.
Электрическая цепь представляет собой совокупность связанных определенным образом источников, потребителей (или соответственно активных и пассивных элементов) и преобразователей электрической энергии.
Цепь называют пассивной, если она состоит только из пассивных элементов, и активной, если в ней также содержатся активные элементы.
Источником электрической энергии называют элемент электрической цепи, осуществляющий преобразование энергии неэлектрического вида в электрическую. Например: гальванические элементы и аккумуляторы преобразуют химическую энергию, термоэлементы – тепловую, электромеханические генераторы – механическую.
Потребителем электрической энергии называют элемент электрической цепи, преобразующий электрическую энергию в неэлектрическую. Например: лампы накаливания – в световую и тепловую, нагревательные приборы – в тепловую, электродвигатель – в механическую.
Преобразователем электрической энергии называют устройство, изменяющее величину и форму электрической энергии. Например: трансформаторы, инверторы преобразуют постоянный ток в переменный, выпрямители – переменный ток в постоянный, устройства для преобразования частоты.
Для того чтобы выполнить расчет, необходимо каждое электротехническое устройство представить его схемой замещения. Схема замещения электрической цепи состоит из совокупности идеализированных элементов, отображающих отдельные свойства физически существующих устройств. Так, идеализированный резистор (сопротивление R) учитывает преобразование электромагнитной энергии в тепло, механическую работу или ее излучение. Идеализированный конденсатор (емкость С) и катушка индуктивности (индуктивность L) характеризуются способностью накапливать энергию соответственно электрического и магнитного поля.
Объединение источников, потребителей и соединительных проводов образует электрическую цепь, на каждом участке которой может действовать электрическое напряжение и протекать электрический ток. Эти напряжения и токи в общем случае могут быть постоянными и переменными во времени и зависеть от свойств элементов цепи. В данном разделе будут рассматриваться постоянные токи и напряжения.
Реальные электрические цепи изучаются на моделях, которые изображаются с помощью условных обозначение в виде электрических схем.
Напряжение U на элементе электрической цепи обозначается на схеме (рис. 1.1.) знаками «+» и «–», имеющими смысл только при совместном рассмотрении, т.к. знак «+» указывает на точку с относительно более высоким потенциалом.
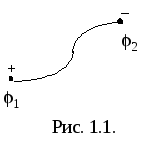
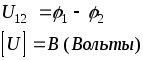 (1.1)
(1.1)
Ток I в элементе электрической цепи обозначается стрелкой на схеме (рис. 1.2.) и указывает направление упорядоченного перемещения положительных электрических зарядов, если ток I выражается положительным числом.
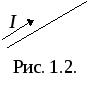
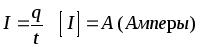 (1.2)
(1.2) 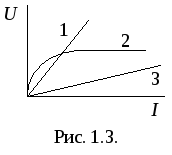
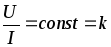 или его отклонение от постоянной величины
невелико. В данном случае, когда ВАХ
изображается линией, близкой к прямой,
считают, что потребитель подчиняетсязакону Ома, согласно
которому напряжение и ток пропорциональны
друг другу.
или его отклонение от постоянной величины
невелико. В данном случае, когда ВАХ
изображается линией, близкой к прямой,
считают, что потребитель подчиняетсязакону Ома, согласно
которому напряжение и ток пропорциональны
друг другу.Этот коэффициент пропорциональности k называют электрическим сопротивлением элемента R, которое измеряется в Омах (Ом).
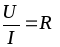 или
или 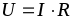 ,
,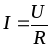 (1.3)
(1.3)
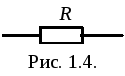
Обозначение резистора на электрических схемах изображено на рис. 1.4.
Величину, обратную
сопротивлению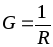 ,
называютпроводимостью, которая
измеряется в Сименсах (См).
,
называютпроводимостью, которая
измеряется в Сименсах (См).
Закон Ома можно представить через проводимость:
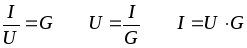 (1.4)
(1.4)
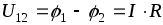 (1.5)
(1.5)
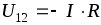 .
.Таким образом, в ТОЭ потребитель моделируется идеальным потребителем, свойства которого определяются значением единственного параметра (R или G).
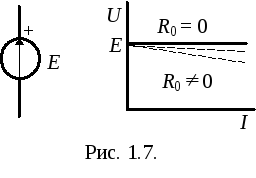
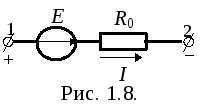
Источники энергии моделируются с помощью источника ЭДС (Е), или источника напряжения, и источника тока (J). ВАХ источников энергии – это внешние характеристики, обычно имеющие ниспадающий характер, т.к. в большинстве случаев с увеличением тока напряжение источника уменьшается.
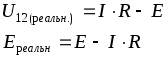 (1.6)
(1.6)Таким образом, свойства источника ЭДС или реального источника напряжения определяются двумя параметрами – вырабатываемой ЭДС Е и внутренним сопротивлением R0.
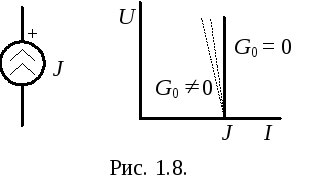
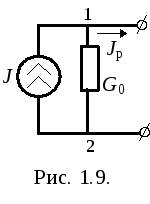
Идеализированный источник тока – это элемент цепи, ток которого не зависит от напряжения и является заданной постоянной величиной, ему соответствует сплошная ВАХ на рис. 1.8.
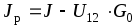 ,
(1.7)
,
(1.7)где J, G0– постоянные параметры.
Таким образом, свойства источника задающего тока определяются двумя параметрами: задающим током J и внутренней проводимостью G0. Чем меньше G0, тем ближе характеристика реального источника тока к идеализированному.
Поскольку внутренние сопротивления реальных источников всегда можно отнести к потребителям цепи далее рассматриваются только идеализированные источники напряжения и тока.
Провода, связывающие потребители и источники, по своей сущности также относятся к потребителям энергии. Однако, часто провода наделяют лишь соединительными функциями и считают, что они служат лишь для того, чтобы показать, как связаны между собой отдельные элементы цепи. Сопротивления проводов, если ими нельзя пренебречь, учитываются включением в соответствующих местах цепи дополнительных потребителей.
Таким образом, в теории линейных электрических цепей объектом изучения является расчетная модель, состоящая из потребителей и идеализированных источников, конфигурация и свойства элементов которой определены условиями задачи.
При решении задач большое значение придается структуре электрической цепи (топологии), определяемой характером связей между элементами.
Введение
Роль и значение электрической энергии в жизни и экономической деятельности человека общеизвестны. Благодаря удобству ее получения, передачи на расстояние и распределения между потребителями она получила широкое распространение и стала основой современной техники, базой для развития промышленности, транспорта, сельского хозяйства, связи, нашла свое место в медицине и образовании, прочно вошла в быт.
Вся область практического применения электрических и магнитных явлений получила название электротехники. Все ее отрасли тесно связаны между собой, технические средства построены на общих принципах, подчиняются одним и тем же законам. Базой для исследования этих принципов и законов стал курс “Теоретические основы электротехники” (ТОЭ), задачами которого являются анализ электромагнитных процессов и явлений, изучение механизма действия электрических машин и аппаратов, разработка и обобщение методов расчета различных электротехнических устройств. Курс ТОЭ имеет большое значение в формировании научного мировоззрения инженера-электрика. На нем базируются все специальные электротехнические дисциплины.
Предлагаемое учебное пособие ставит целью помочь студенту разобраться в сложных теоретических вопросах, понять суть изучаемых явлений, научиться решать конкретные практические задачи. Пособие не является в полном смысле учебником по ТОЭ. Оно включает в себя только отдельные разделы курса. Ряд вопросов излагается без доказательств и подробных выводов. Для лучшего усвоения материала в пособие включено большое количество численных примеров с решениями.
Пособие предназначено для студентов, обучающихся без отрыва от производства и изучающих ТОЭ самостоятельно.
1. Линейные электрические цепи постоянного тока
1.1. Электрическая цепь и ее элементы
Электрическая цепь представляет собой совокупность устройств, предназначенных для производства, передачи и потребления электрической энергии. Пример простейшей электрической цепи показан на рис. 1.1. Кружок со стрелкой внутри и стоящей рядом буквой Е (рис. 1.1, а) обозначает так называемый источник ЭДС (его еще называют источником напряжения). Это идеализированный источник энергии, внутреннее сопротивление которого равно нулю, а напряжение постоянно по величине, равно ЭДС реального источника и не зависит от протекающего по нему тока. Стрелка показывает направление возрастания потенциала внутри источника. Плюс находится у острия, минус – у хвоста стрелки. Ток во внешней цепи протекает по направлению стрелки ЭДС – от плюса источника к минусу. Внутреннее сопротивление реального источника R0 соединяется последовательно с ЭДС Е, и в совокупности они образуют схему замещения реального источника (на рис. 1.1, а обведена пунктиром).
а) б)
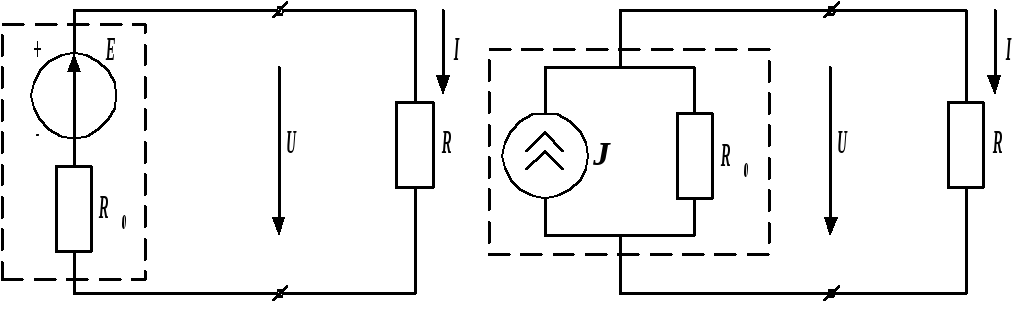
Рис. 1.1. Простейшая электрическая цепь
Другое представление схемы генератора осуществляется в виде параллельного соединения источника тока и сопротивления R0 (рис. 1.1, б). Под источником тока понимают также идеализированный источник энергии, внутреннее сопротивление которого бесконечно велико, и который вырабатывает ток J, не зависящий от величины нагрузки R и равный частному от деления ЭДС реального источника на его внутреннее сопротивление J = E/R0. На схеме он изображается кружком с двойной стрелкой, рядом с которым ставится буква J (рис. 1.1, б).
В схеме рис. 1.1, а ЭДС равна сумме напряжений на нагрузке и внутреннем сопротивлении источника:
Е = U + IR0.
Отсюда
U = E – IR0. (1.1)
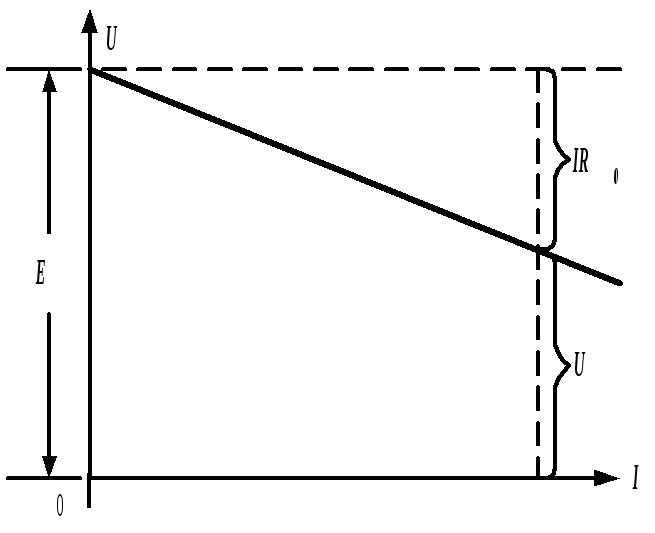
Рис. 1.2. Внешняя характеристика генератора
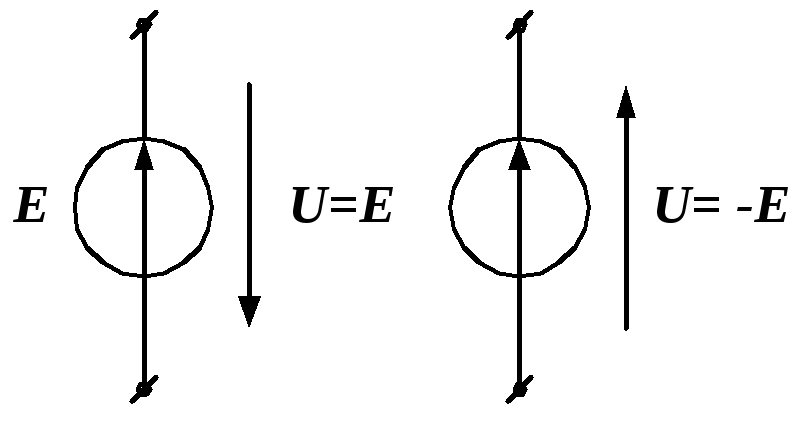
а)
б)
Рис. 1.3. Напряжение на зажимах источника
Последнее выражение представляет так называемую внешнюю характеристику генератора. Оно говорит о том, что напряжение на его зажимах меньше ЭДС на величину падения напряжения на внутреннем сопротивлении (рис. 1.2). Чем больше ток и внутреннее сопротивление генератора, тем меньше выдаваемое им напряжение. При холостом ходе генератора (при I = 0) напряжение, измеренное на его разомкнутых зажимах равно ЭДС: U = E.На практике часто приходится сталкиваться с элементами схемы, показанными на рис. 1.3. Разница между ними заключается во взаимном направлении стрелок ЭДС и напряжения. В первом случае (рис. 1.3, а), когда эти стрелки направлены противоположно друг другу, напряжение определяется как разность потенциалов положительного и отрицательного зажимов источника и поэтому положительно. При одинаковых направлениях стрелок E и U (рис. 1.3, б) напряжение равно разности отрицательного и положительного потенциалов, а потому оно отрицательно: U = – E.
Пример 1.1. Напряжение холостого хода батареи равно 16,4 В. Чему равно ее внутреннее сопротивление, если при токе во внешней цепи, равном 8 А, напряжение на ее зажимах равно 15,2 В?
Р е ш е н и е. В соответствии с уравнением (1.1) из схемы, показанной на рис. 1.4, а, следует U = UX = E = 16,4 В.
Схема
1.4, б дает 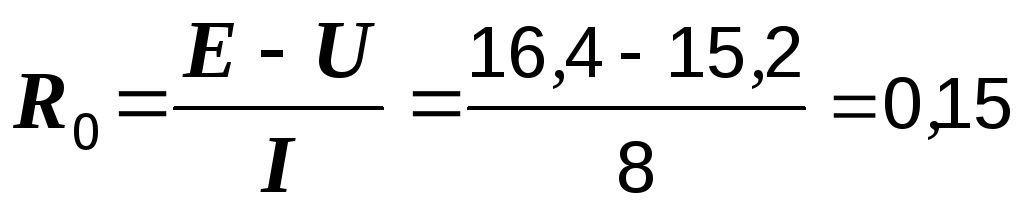 Ом.
Ом.
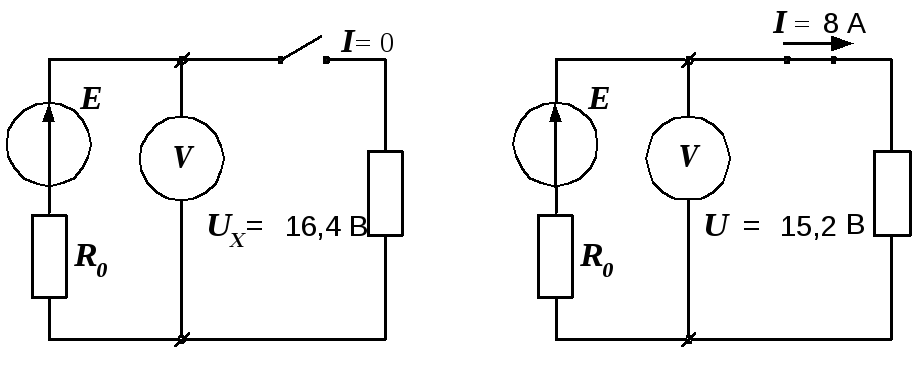
а)
б)
Рис. 1.4. Разомкнутая (а) и замкнутая (б) цепи
При решении задачи мы полагали, что измерение проводилось идеальным вольтметром, имеющим бесконечно большое сопротивление. При конечной величине сопротивления вольтметра в измерение вносится погрешность.
П
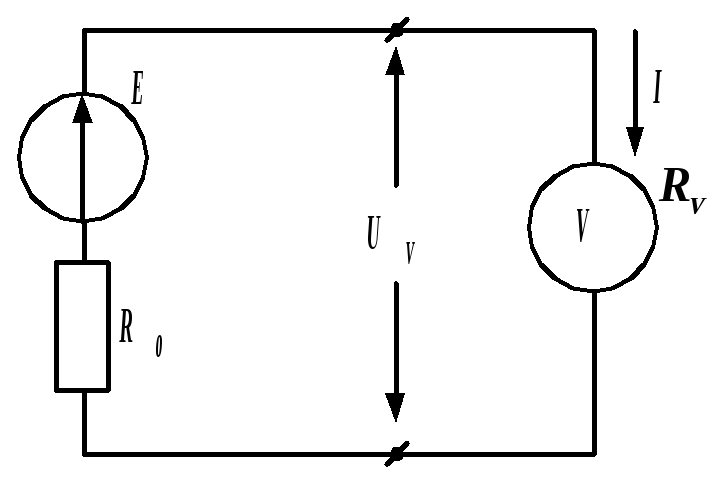
Рис. 1.5. Измерение ЭДС вольтметром
ример 1.2. ЭДС батареи измеряется вольтметром, имеющим сопротивление RV. Чему равно показание вольтметра при трех различных значениях его сопротивления, если Е = 80 В,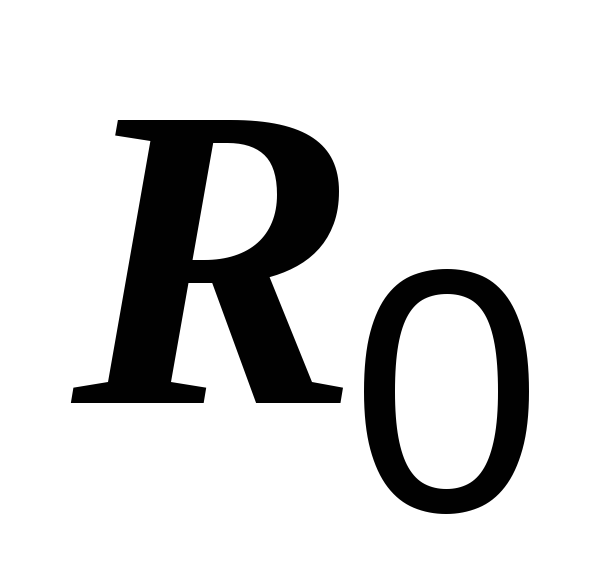 =
100 Ом?
=
100 Ом?Р е ш е н и е. Показание вольтметра UV равно падению напряжения на его сопротивлении (рис. 1.5):
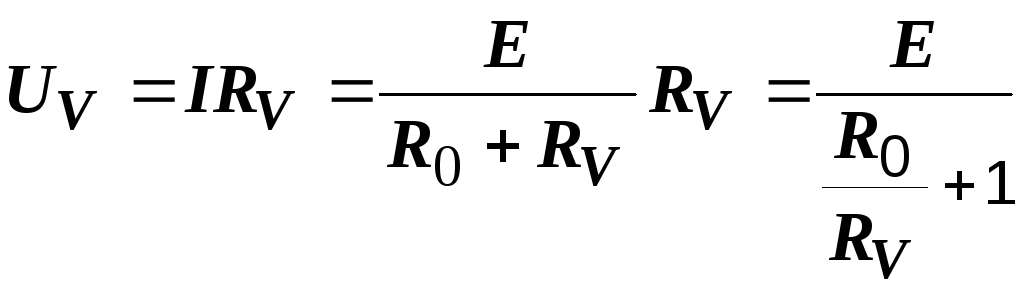 ;
(1.2)
;
(1.2)
а) RV =
100 кОм: 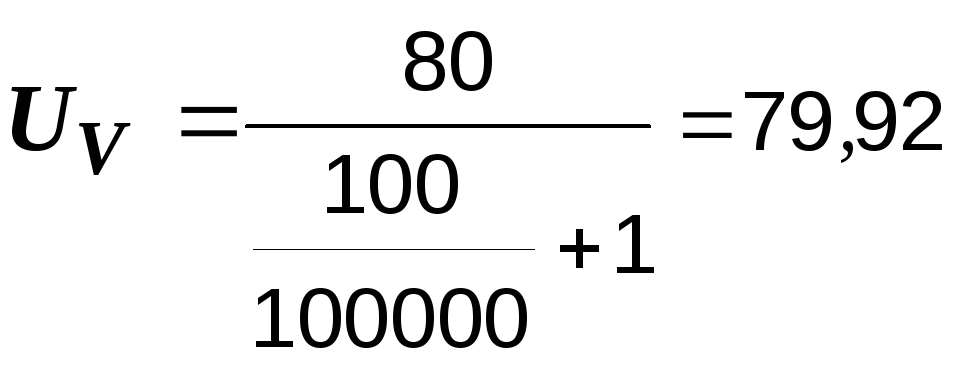 В;
В;
б) RV =
2,5 кОм: 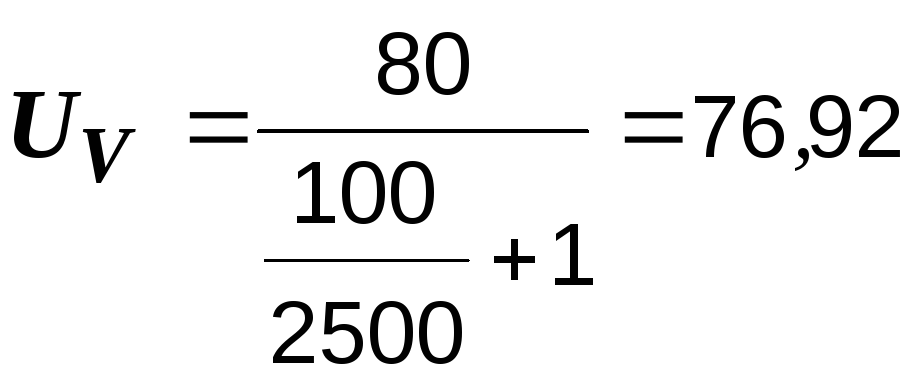 В;
В;
в) RV =
400 Ом: 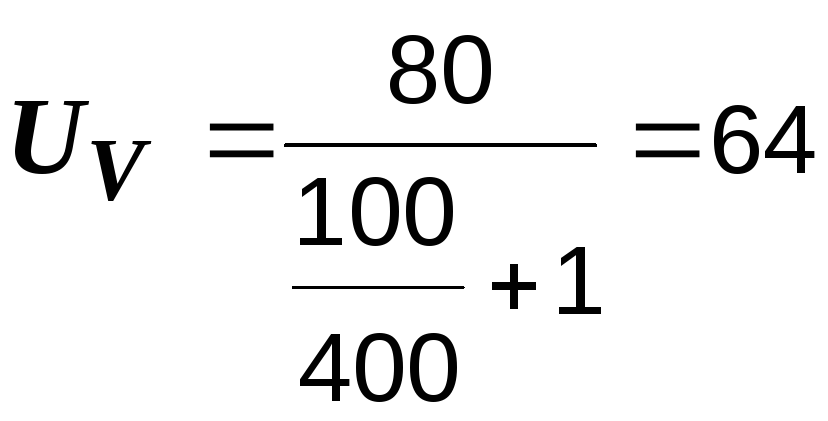 В.
В.
Чем больше сопротивление вольтметра, тем меньше погрешность измерения. Как следует из формулы (1.2), только при RV показание вольтметра равно ЭДС: UV = E.
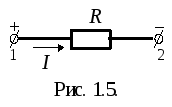
Нагрузкой в схеме на рис. 1.1 служит сопротивление R. Напряжение на его зажимах связано с током законом Ома
I = GU, (1.3)
где G – проводимость, величина, обратная сопротивлению R; единица измерения – cименс (См).
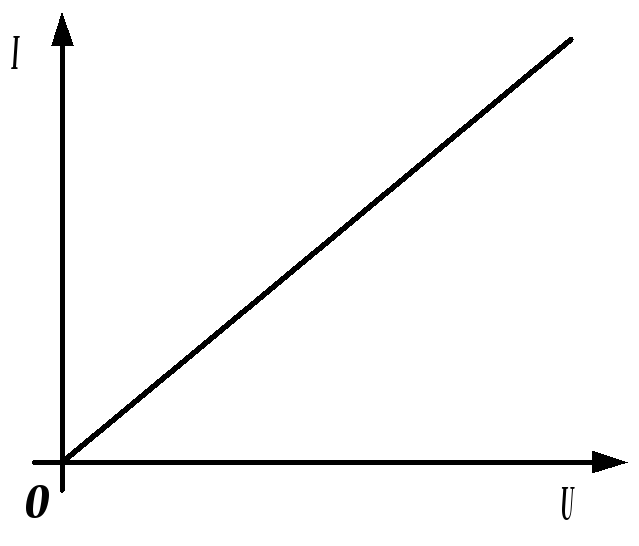
Рис. 1.6. Вольтамперная характеристика линейного сопротивления
При G = const выражение (1.3) представляет собой уравнение прямой, проходящей через начало координат. Его график (рис. 1.6) называется вольтамперной характеристикой. Элементы электрической цепи, имеющие аналогичную (прямолинейную) вольтамперную характеристику, называются линейными. Электрическая цепь, состоящая только из линейных элементов, также называется линейной. Полагая
в уравнении (1.3) 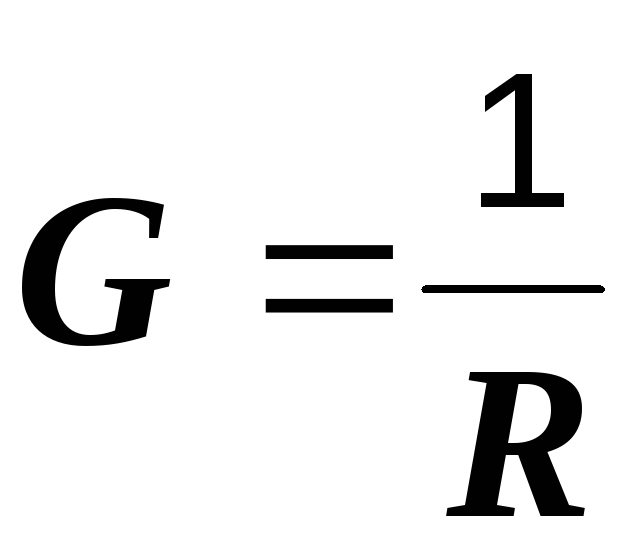 ,
получим U
= IR.
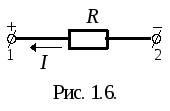
Последнее выражение справедливо, когда
стрелки напряжения и тока у резистора
направлены в одну сторону (рис. 1.7, а).
При изменении на схеме направления
любой из стрелок в правой части закона
Ома следует ставить минус (рис. 1.7, б).
Здесь при определении напряжения на
элементе мы «идем по стрелке»
напряжения против стрелки тока.
,
получим U
= IR.
Последнее выражение справедливо, когда
стрелки напряжения и тока у резистора
направлены в одну сторону (рис. 1.7, а).
При изменении на схеме направления
любой из стрелок в правой части закона
Ома следует ставить минус (рис. 1.7, б).
Здесь при определении напряжения на
элементе мы «идем по стрелке»
напряжения против стрелки тока.
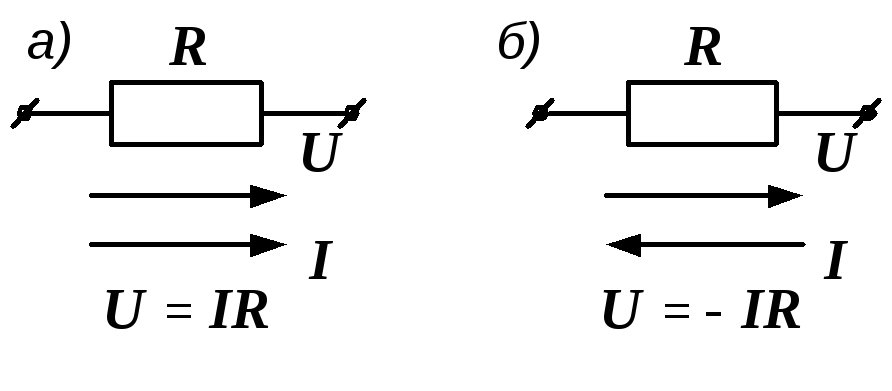
Рис. 1.7. Напряжение и ток в сопротивлении
Рядом с буквой U можно ставить два индекса, обозначающие точки, между которыми определяется напряжение; например, Uab – напряжение между точками а и b. При этом направление стрелки напряжения на схеме определяется порядком следования индексов – от а к b (от первого индекса ко второму).Раздел №1. Электротехника. Тема №1. Линейные электрические цепи постоянного тока
1.1.Элементы электрических цепей постоянного тока
Электромагнитные устройства с происходящими в них физическими процессами можно заменить некоторым расчетным эквивалентом – электрической цепью (ЭЦ).
Электрической цепью называют совокупность источников электрической энергии, соединенных с нагрузками. Электромагнитные процессы в ЭЦ можно описать с помощью понятий: ток – I (А), напряжение – U (В), электродвижущая сила (ЭДС) – Е (В), электрический потенциал в точке а – φa, сопротивление – R (Ом), проводимость – g (См), индуктивность – L (Гн), емкость – С (Ф).
Постоянный ток, не изменяющийся во времени ни по величине, ни по направлению, представляет собой упорядоченное «направленное» движение электрических зарядов. Носителями зарядов в металлах являются электроны, в полупроводниках – дырки и электроны, в жидкостях – ионы, в газовом разряде – электроны и ионы. Упорядоченное движение носителей зарядов в проводнике вызывается электрическим полем, создаваемым источниками электрической энергии.
Источник энергии характеризуется величиной и направлением ЭДС и величиной внутреннего сопротивления.
На рис. 1.1а) изображена схема неразветвленной электрической цепи.
а)
б)
в)
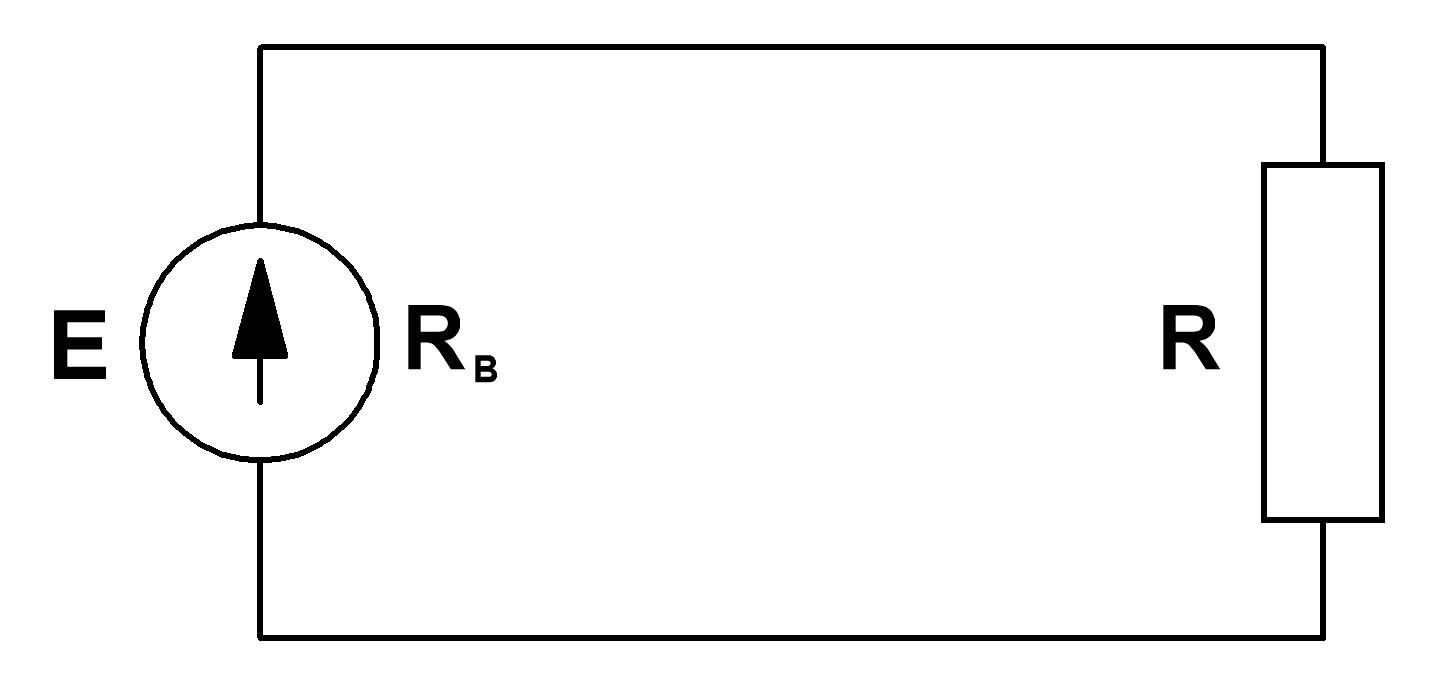
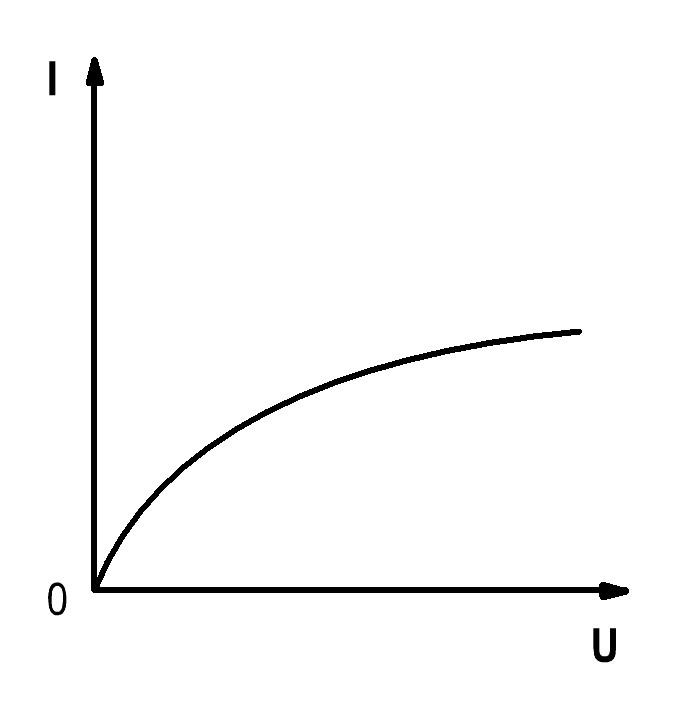
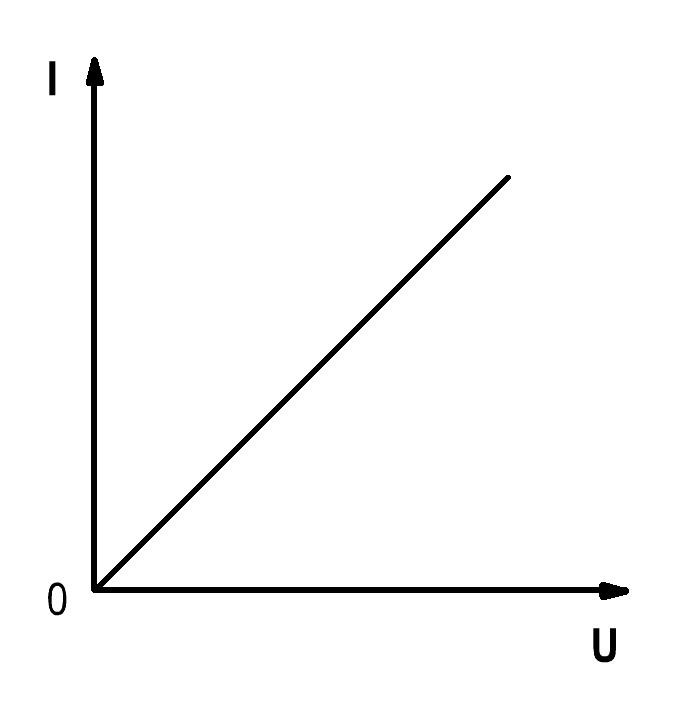
Рис. 1.1.
Зависимость протекающего по сопротивлению R тока от напряжения на этом сопротивлении I=f(U), называется вольтамперной характеристикой (ВАХ). Сопротивления, ВАХ которых – прямые линии (рис.1.1.б.), называются линейными, а электрические цепи с такими сопротивлениями – линейными электрическими цепями. Сопротивления, ВАХ которых не являются прямыми линиями, называют нелинейными (рис. 1.1.в.), а электрические цепи с таким сопротивлениями − нелинейными. В неразветвленной цепи через каждый участок протекает один и тот же ток. В разветвленной цепи, представленной на рис.1.2., в каждой ветви протекает свой ток.
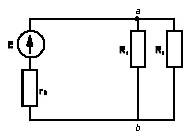
Рис. 1.2.
Ветвью называется участок цепи, образованный последовательно соединенными элементами, заключенными между двумя узлами а и b (рис.1.2.). Узел – это точка цепи, в которой сходится не менее трех ветвей. Если в месте пересечения двух линий нет электрического соединения, то точка не ставится.
1.2. Закон Ома для участка цепи
Напряжение Uab на участке a—b ЭЦ (рис.1.3.) понимают разность потенциалов
между крайними точками этого участка.
Ток I течет от точки «а» большего потенциала к точке «b» меньшего потенциала, т.е. 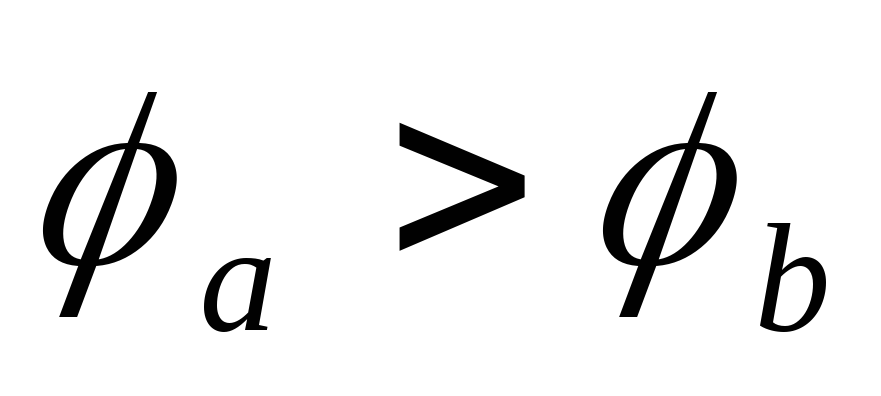 на величину падения напряжения на
сопротивленииR
на величину падения напряжения на
сопротивленииR
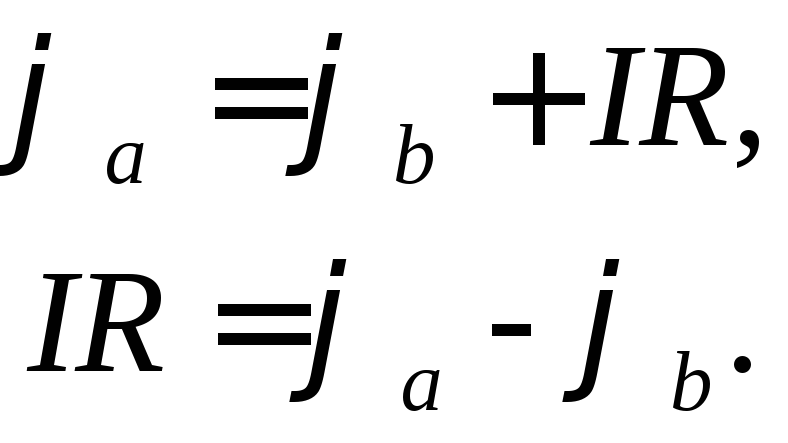
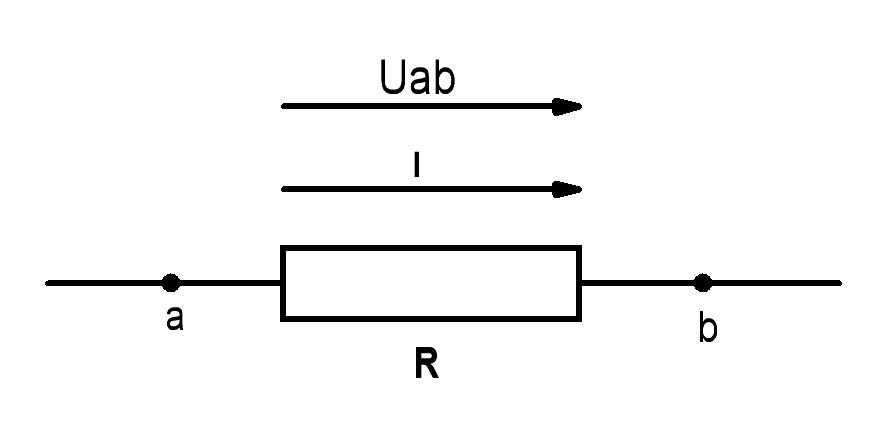
Рис. 1.3.
В соответствии с определением напряжение между точками а и b:

Тогда напряжение на сопротивлении R равно произведению протекающего по нему тока на величину этого сопротивления. Так определяется закон Ома для участка цепи, не содержащего ЭДС, который можно записать как
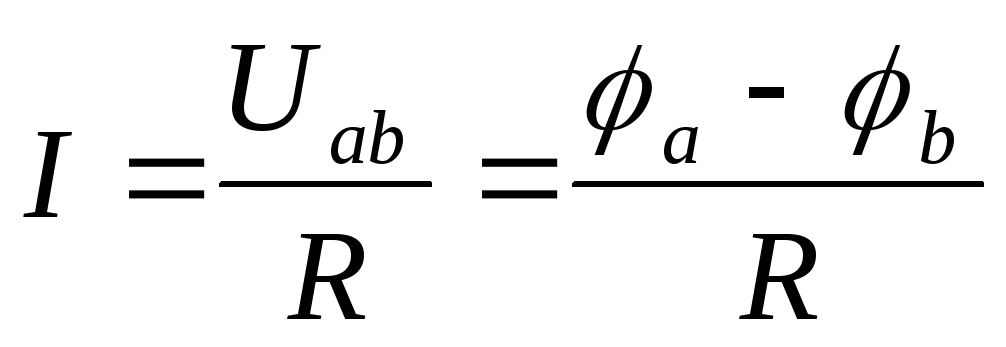
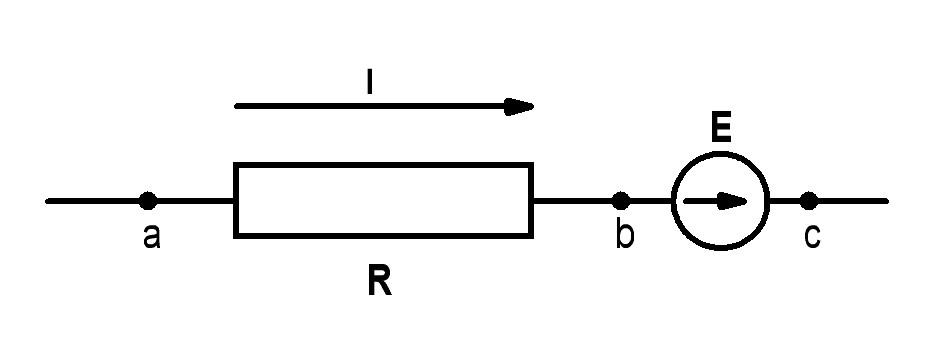
Рассмотрим участок цепи, содержащий помимо сопротивления ЭДС, Е.
а)
б)
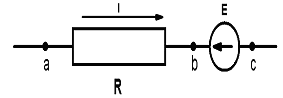
Рис. 1.4.
На рис. 1.4. (а и б) показаны участки цепей с источником ЭДС, по которым протекает ток I. Найдем разность потенциалов (напряжение) между точками «а» и «с». Согласно определению в обоих случаях имеем
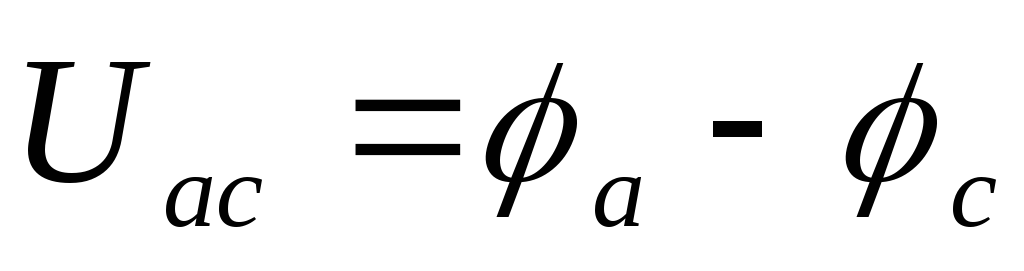 .
.
На рис.1.4.а)
перемещение от точки «с» к точке «b» является встречным направлению ЭДС Е,
поэтому 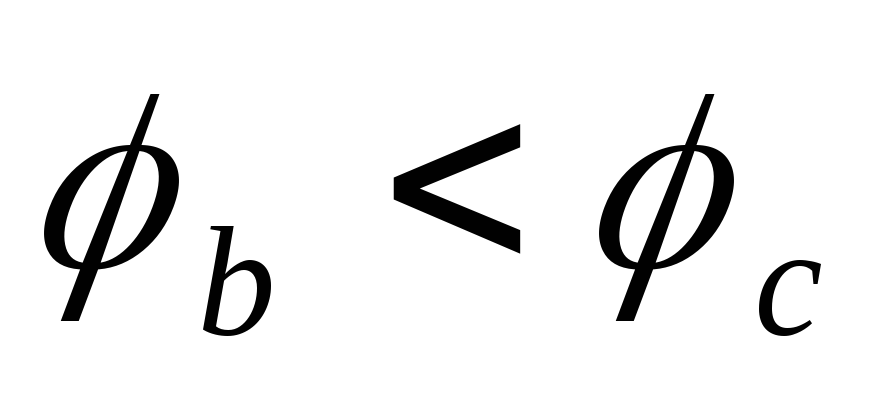 на величинуЕ
на величинуЕ
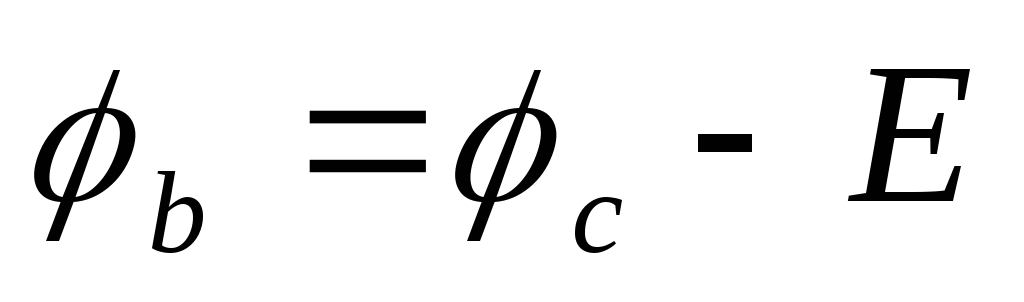 .
.
Потенциал в точке «b» на рис. 1.4.б) оказывается выше, чем в точке с на величину ЭДС Е
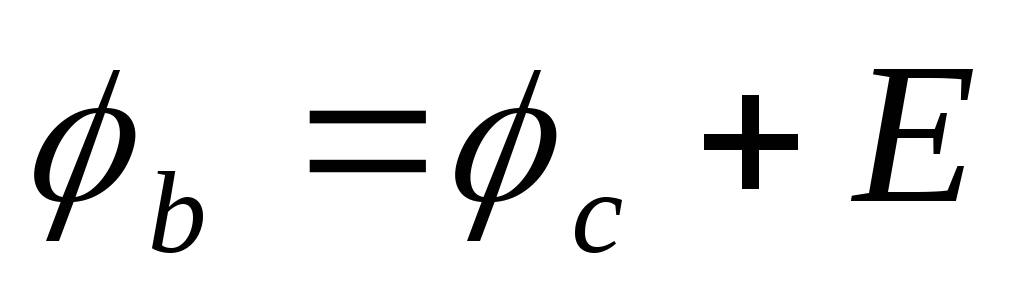 .
.
Поскольку ток течет от более высокого потенциала к более низкому, в обеих схемах а и b рис. 1.4. потенциал точки а выше потенциала точки b на величину падения напряжения на сопротивлении R
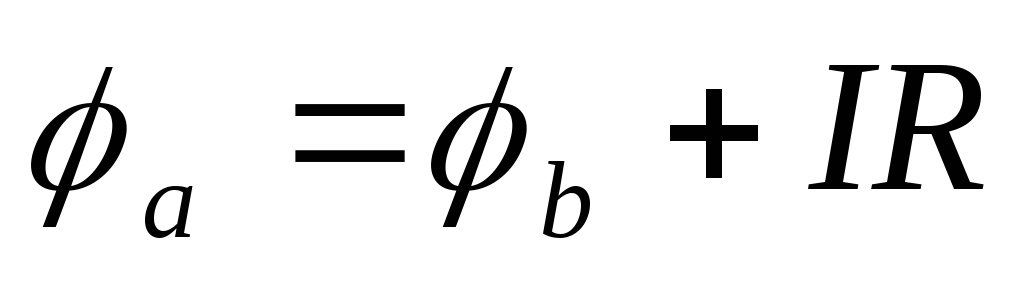 .
.
Таким образом, на рис. 1.4.а)
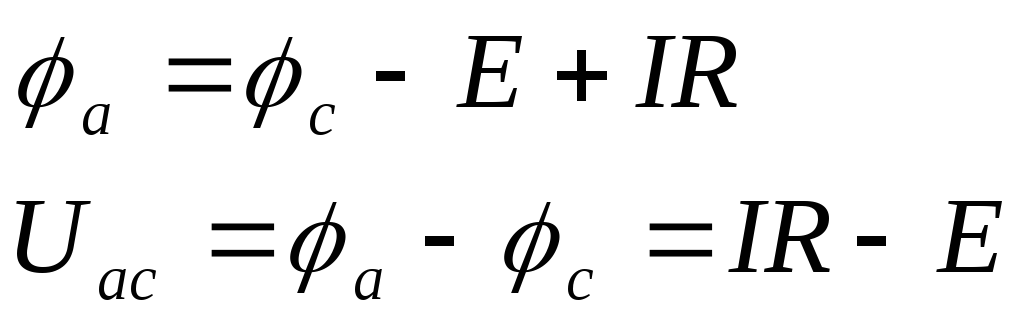 ,
,
а на рис. 1.4.б).
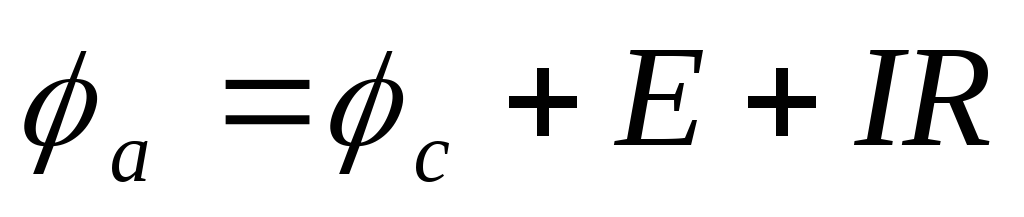 ,
или
,
или 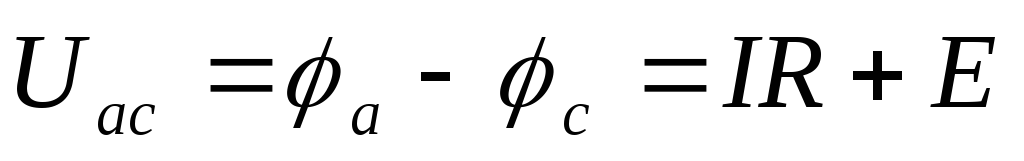 .
.
Т.о., для участка
цепи, содержащего источник ЭДС, можно
найти ток этого участка по разности
потенциалов 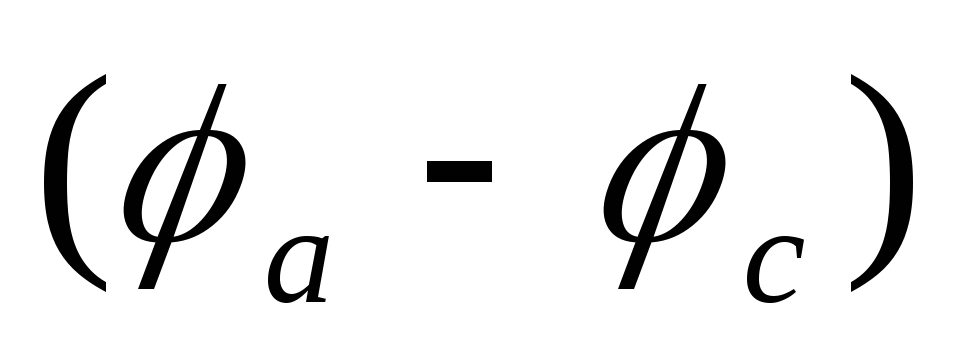 .
.
Ток для схемы рис.
1.4.а) 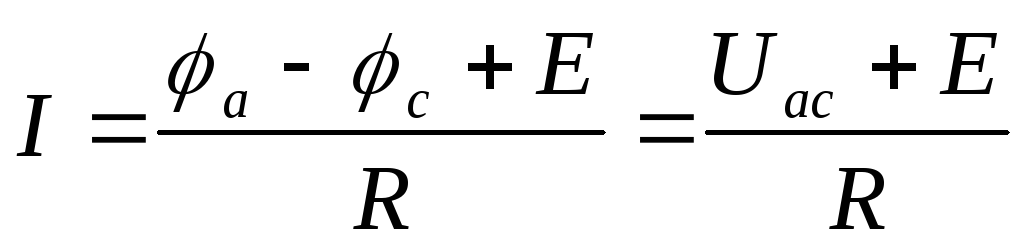 ,
,
для схемы рис.1.4.б) 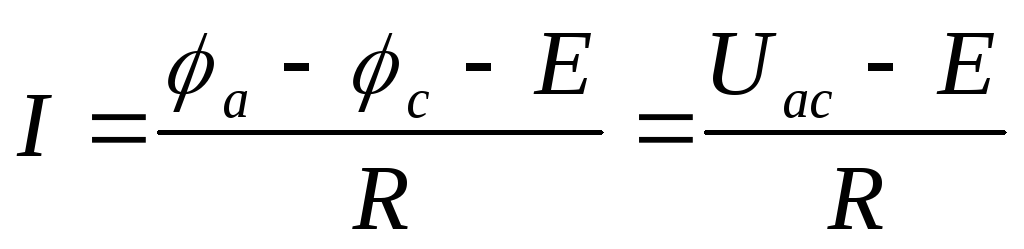 .
.
Полученные уравнения выражают закон Ома для участков цепи, включающих источники ЭДС, направленные по току и против тока.
1. Линейные электрические цепи постоянного тока. 1, 2 законы Кирхгофа.
Последовательность расчета линейных электрических цепей с помощью законов Кирхгофа:
произвольно задаются положительные направления токов в ветвях;
обозначают направления обхода контуров;
записывают уравнения по первому и второму законам Кирхгофа;
решают уравнения;
проверяют правильность расчета, составляя энергетический баланс.
Первый закон Кирхгофа:
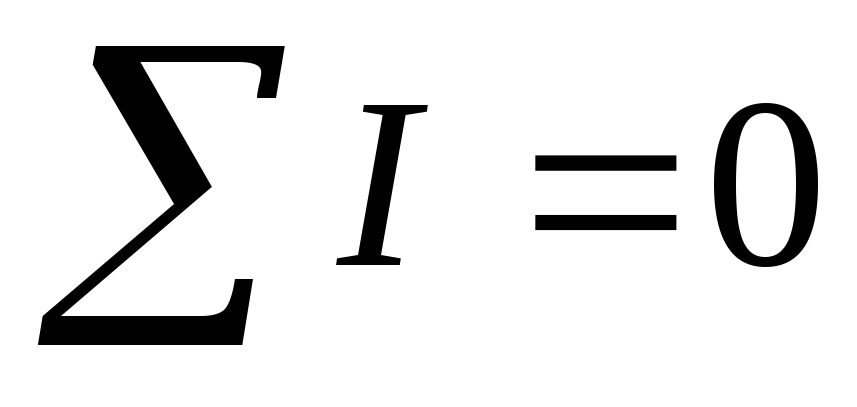
Формулировка:Алгебраическая сумма токов ветвей, сходящихся в узле равна нулю, при этом токи, направленные от узла, следует брать со знаком плюс, а токи, направленные к узлу, — со знаком минус.
Второй закон Кирхгофа:
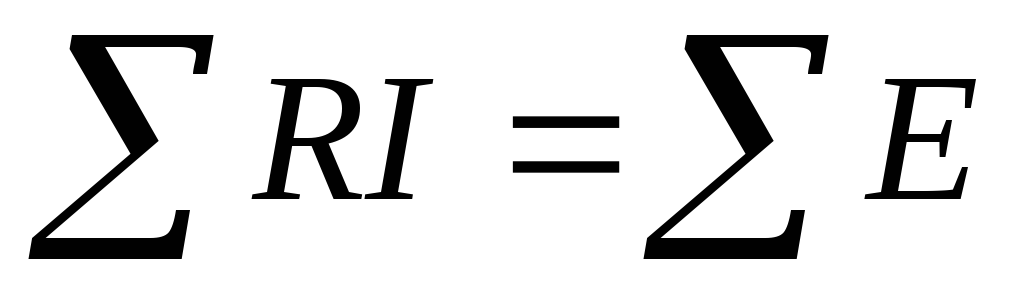
Формулировка:Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме э.д.с., входящих в контур. Слагаемые берут со знаком плюс в случае, когда направление обхода контура совпадает с направлением соответсвенно напряжения, тока или э.д.с., в противном случае слагаемые берут с отрицательным знаком.
Если в цепи имеется x ветвей и у узлов, в том числе xi –ветвей с источниками токов, то необходимо составить x–xi уравнений для определения токов во всех ветвях. При этом по первому закону Кирхгофа составляют у–1 уравнений, а все остальные x–xi–(у–1) уравнения – по второму закону Кирхгофа.
Для проверки правильности расчетов определяют сумму мощностей, генерируемых источниками, и сравнивают ее с суммой мощностей всех потребителей
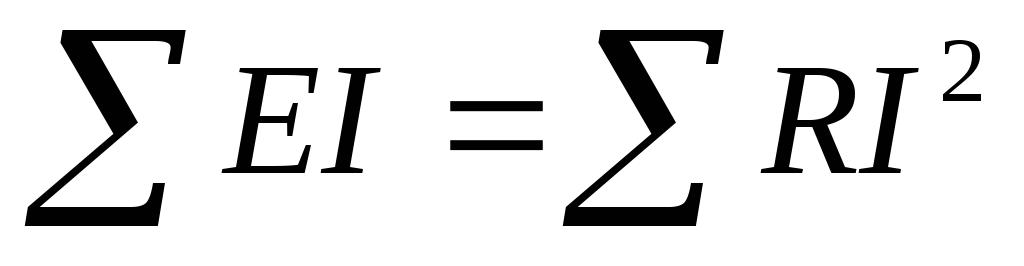 .
.
Слагаемые I2R всегда положительны, а слагаемые EI берут со знаком минус, когда направления E и I встречные. Если баланс не получается, то токи определены неправильно.
2. Методы расчёта электрических цепей постоянного тока.
Метод контурных токов:
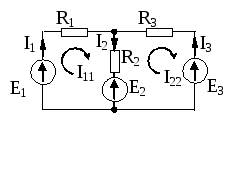 Ток
в любой ветви электрической схемы можно
представить в виде суммы нескольких
токов, каждый их которых замыкается по
своему контуру, оставаясь вдоль него
неизменным. Такие составляющие
действительных токов называют контурными
токами. На
рис. действительный
ток I2 можно представить как разность контурных
токов I11 и I22,
т.е.
Ток
в любой ветви электрической схемы можно
представить в виде суммы нескольких
токов, каждый их которых замыкается по
своему контуру, оставаясь вдоль него
неизменным. Такие составляющие
действительных токов называют контурными
токами. На
рис. действительный
ток I2 можно представить как разность контурных
токов I11 и I22,
т.е.
I2=I11–I22 .
При этом уравнение по второму закону Кирхгофа, составленное для 1-го контура, имеет вид I1R1+I2R2=E1–E2, или с учетом предыдущего уравненияI11R1+(I11–I22)R2=E1–E2.
Аналогично для другого контура
I2R2+I3R3=E3–E2 или (I11–I22)R2–I22R3=E3–E2.
Преобразуем уравнения 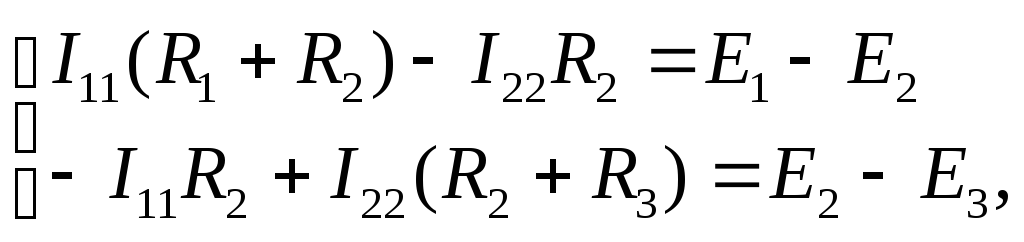
или иначе I11R11–I22R12=E11
–I11R21+I22R22=E22,
где R11 – сумма сопротивлений всех ветвей, входящих в первый контур; R12 – сопротивление ветви, общей для первого и второго контура; E11 – сумма всех ЭДС, входящих в первый контур.
Соответствующие ЭДС берутся со знаком «минус», если они направлены против направления обхода контура. Аналогичные величины получаются для второго контура.
Метод наложения (суперпозиции):
Для линейных цепей ток в k-ветви равен сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Это позволяет проводить расчеты электрических цепей методом наложения – сначала определить все токи от одной ЭДС, затем от другой и т.д., а потом все составляющие токов от разных ЭДС сложить. Отметим, что мощности от частичных токов суммировать нельзя – в баланс мощностей должны входить полные токи.
Принцип взаимности:
Для линейной цепи ток в k-ветви Ik, вызванный источником Em, находящимся в m-ветви, равен току Im в m-ветви, вызванным источником Em, если источник Em перенести в k-ветвь , т.е. Ik=Emgkm=Emgmk.
Принцип компенсации:
В любой электрической цепи без изменений токораспределения можно заменить сопротивление источником ЭДС, величина которого равна падению напряжения на сопротивлении и направлена встречно току на этом сопротивлении. Аналогичную замену можно сделать и источником тока J, величина которого равна току в этом сопротивлении и направлена на ту же сторону. Это следует из второго и соответственно первого законов Кирхгофа при переносе слагаемого из левой части уравнения в правую.
3. Нелинейные электрические цепи постоянного тока и методы их расчета.
В электрические цепи могут входить элементы, сопротивление которых не является величиной постоянной, а зависит от напряжения и силы тока. Вольт-амперная характеристика (ВАХ) такого элемента имеет нелинейный вид, поэтому элемент называется нелинейным (НЭ). Электрическая цепь, в которую входит хотя бы один нелинейный элемент, называется нелинейной. К нелинейным элементам относятся полупроводниковые приборы, лампы накаливания и др. На рис.1 приведена ВАХ одного из НЭ.
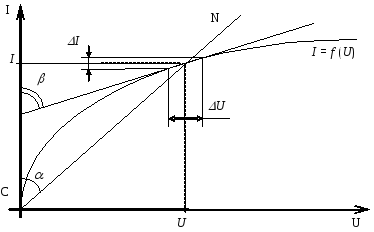
Каждой
точке ВАХ НЭ соответствует определенное
сопротивление 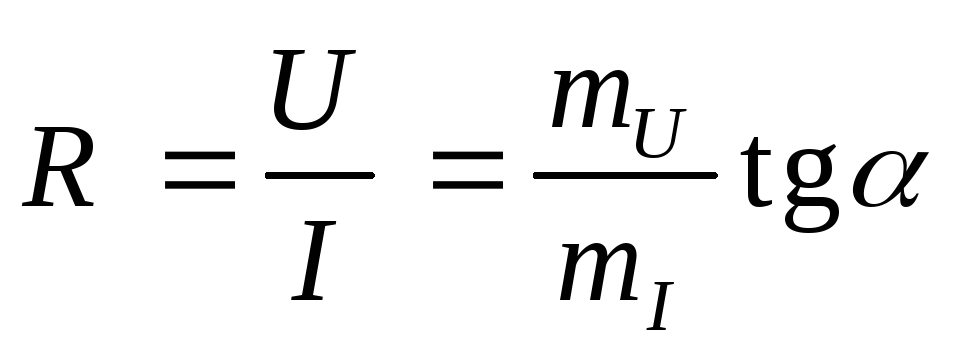 ,
которое пропорционально тангенсу угла
наклона прямой CN к оси токов. Это
сопротивление называетсястатическим и представляет собой сопротивление
элемента постоянному току. Кроме
статического сопротивления НЭ для
каждой точки характеристики можно
определить так называемое дифференциальное сопротивление Rдиф,
которое равно отношению приращения
напряжения U к приращению тока I,
стремящегося к нулю:
,
которое пропорционально тангенсу угла
наклона прямой CN к оси токов. Это
сопротивление называетсястатическим и представляет собой сопротивление
элемента постоянному току. Кроме
статического сопротивления НЭ для
каждой точки характеристики можно
определить так называемое дифференциальное сопротивление Rдиф,
которое равно отношению приращения
напряжения U к приращению тока I,
стремящегося к нулю:
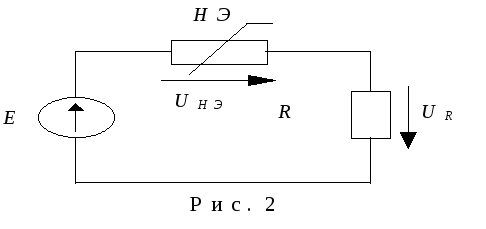
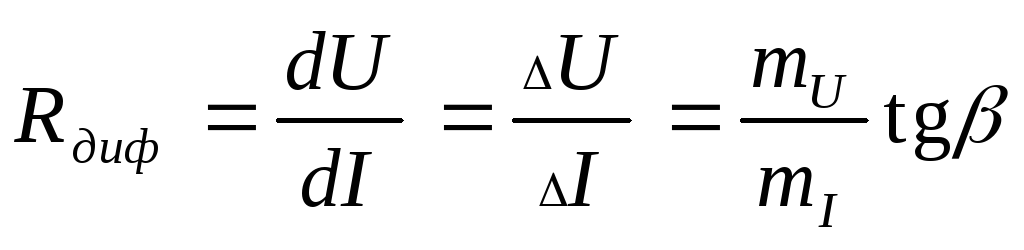 ,
,т.е. пропорционально тангенсу угла наклона касательной в данной точке характеристики к оси токов. Дифференциальное сопротивление характеризует НЭ при малых изменениях напряжения и тока. При расчете нелинейной цепи с последовательным соединением линейного и нелинейного элемента часто используют метод нагрузочной характеристики.
Для цепи, показанной на рис. 2, согласно второму закону Кирхгофа можно записать:
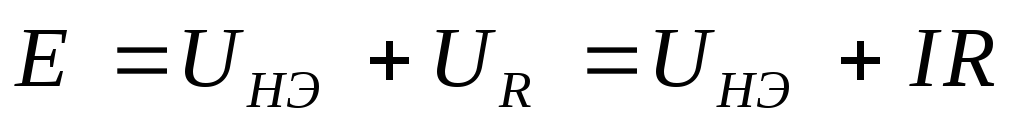 ,
,
откуда 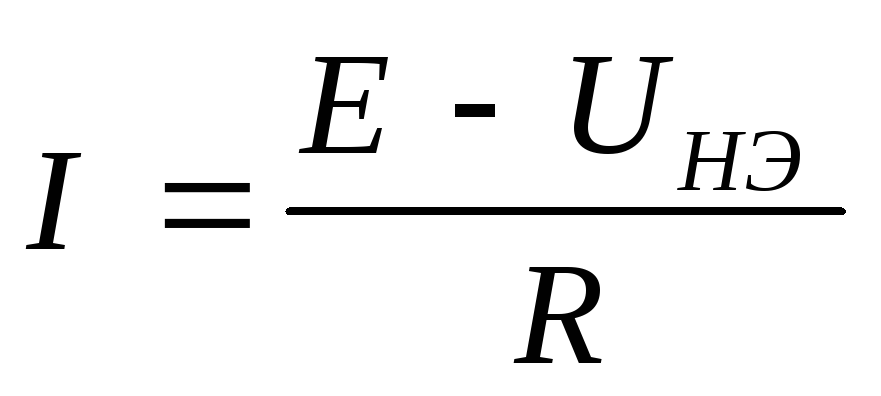 . (1)
. (1)
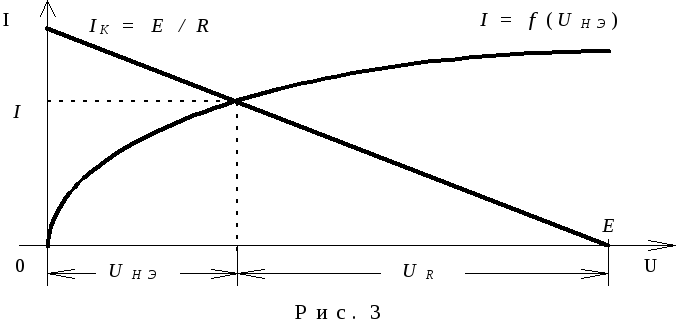
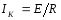 ,
приUНЭ = 0 (короткое замыкание
на нелинейном элементе).
,
приUНЭ = 0 (короткое замыкание
на нелинейном элементе).