как замерить по длине окружности, измерить рулеткой, определить диаметр

Содержание:

В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.

Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.

Определение диаметра в бытовых условиях

До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:

• рулетка или стандартная линейка;
• штангенциркуль;
• фотоаппарат — его задействуют при необходимости.

Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.

В этом случае выполняют измерение диаметра труб в такой последовательности:

1. Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
2. Потом отсчитывают количество делений, соответствующих размеру диаметра.

Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров. Иногда требуется определить и площадь трубопровода, что тоже весьма просто сделать.

Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:

1. Раздвигают его ножки и прикладывают к торцу изделия.
2. Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
3. Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.

Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.

Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности. Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.

Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14. Не намного сложнее узнать объем трубы, выполнив простые расчеты.

Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:

d – определяемый диаметр;

l – длина измеренной окружности.

К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.

Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.

К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.

Измерение диаметров в производственных условиях

На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю. Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.

Документация должна содержать определенную информацию, касающуюся труб:

• номинальные размеры;
• номер и дата ТУ;
• марка металла или вид пластика;
• номер товарной партии;
• итоги проведенных испытаний;
• хим. анализ выплавки;
• тип термической обработки;
• результаты рентгеновской дефектоскопии.

Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:

• наименование производителя;
• номер плавки;
• номер изделия и его номинальные параметры;
• дату изготовления;
• эквивалент углерода.

Длины труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.

Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.

У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:

Δр – толщина материала рулетки;

0,2 миллиметра– припуск на прилегание инструмента к поверхности.

Допускается отклонение величины внешнего диаметра от заявленной производителем:

• для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
• для больших труб – 0,7%.

В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.

Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов. 

trubaspec.com

Диаметр — это… Что такое Диаметр?

Диаметр в изначальном значении это отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Диаметр геометрических фигур

Диаметр окружности, круга, сферы, шара

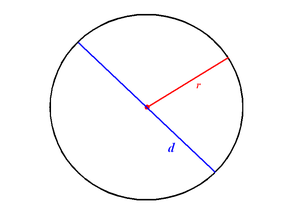Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), и проходящий через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет максимальную длину. По величине диаметр равен двум радиусам.

Символ диаметра

Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как

⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов Юникода» (gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализорованные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или \U+2205 в текстовой строке.

Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.

Следует отличать символ диаметра «⌀» от других похожих на него символов:

Вариации и обобщения

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.

• Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
• Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
  • Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
  • Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
  • Диаметром множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, диаметр n-размерного гиперкуба со стороной s равен

.

См. также

Литература

dic.academic.ru

Диаметр — Википедия. Что такое Диаметр

Материал из Википедии — свободной энциклопедии

Диа́метр в изначальном значении термина — отрезок, соединяющий две точки на окружности и проходящий через центр окружности, а также длина этого отрезка. Диаметр равен двум радиусам.

Диаметр геометрических фигур

Радиус (r) и диаметр (d) окружности

Диаметр — это хорда (отрезок, соединяющий две точки) на окружности (сфере, поверхности шара), проходящая через центр этой окружности (сферы, шара). Также диаметром называют длину этого отрезка. Диаметр окружности является хордой, проходящей через её центр; такая хорда имеет наибольшую длину. По величине диаметр равен двум радиусам.

Символ диаметра

Символы со сходным начертанием: Ø · ø · ∅

Символ диаметра «⌀» (может не отображаться в некоторых браузерах) схож начертанием со строчной перечёркнутой буквой «o». В Юникоде он находится под десятичным номером 8960 или шестнадцатеричным номером 2300 (может быть введён в HTML-код как ⌀ или ⌀). Этот символ не присутствует в стандартных раскладках, поэтому для его ввода при компьютерном наборе необходимо использовать вспомогательные средства — например, приложение «Таблица символов» в Windows, программу «Таблица символов» (ранее gucharmap) в GNOME, команду «Вставка» → «Символ…» в программах Microsoft Office и т. д. Специализированные программы могут предоставлять пользователю свои способы ввода этого символа: к примеру, в САПР AutoCAD для ввода символа диаметра используется сочетание символов %%c (буква c — латинская) или \U+2205 в текстовой строке.

Во многих случаях символ диаметра может не отображаться, так как он редко включается в шрифты — например, он присутствует в Arial Unicode MS (поставляется с Microsoft Office, при установке именуется «Универсальный шрифт»), DejaVu (свободный), Code2000 (условно-бесплатный) и некоторых других.

Сопряжённые диаметры эллипса и гиперболы

Сопряжённые диаметры эллипса

Пара сопряжённых диаметров эллипса. Если в точках касания диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм

• Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.

На рисунке представлена пара сопряженных диаметров (красный и синий). Если в точках пересечения диаметра с эллипсом провести прямую, параллельную сопряжённому диаметру, то прямая будет касательной к эллипсу, и четыре таких касательных ко всем четырём концам пары сопряжённых диаметров эллипса образуют описанный около эллипса параллелограмм (зеленые линии на рисунке).

• Расстояния r1{\displaystyle r_{1}} и r2{\displaystyle r_{2}} от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
• Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле r=abb2cos2⁡φ+a2sin2⁡φ=b1−e2cos2⁡φ{\displaystyle r={\frac {ab}{\sqrt {b^{2}\cos ^{2}\varphi +a^{2}\sin ^{2}\varphi }}}={\frac {b}{\sqrt {1-e^{2}\cos ^{2}\varphi }}}}, где φ{\displaystyle \varphi } — угол между радиус-вектором данной точки и осью абсцисс.

Сопряжённые диаметры гиперболы

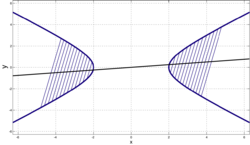Диаметры гиперболы

• Диаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряжённый диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
• Угловой коэффициент k{\displaystyle k} параллельных хорд и угловой коэффициент k1{\displaystyle k_{1}} соответствующего диаметра связан соотношением

k⋅k1=ε2−1=b2a2{\displaystyle k\cdot k_{1}=\varepsilon ^{2}-1={\frac {b^{2}}{a^{2}}}}

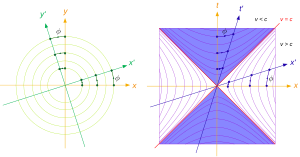Для произвольного угла φ показаны диаметры и сопряженные им диаметры для окружностей и равнобочных гипербол.

• Если диаметр гипербол a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряжёнными.
• Главными диаметрами гипербол называются взаимно сопряжённые и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
• В случае гипербол с асимптотами, образующими прямой угол, её сопряженные гиперболы получатся при её зеркальном отражении относительно одной из асимптот. При таком зеркальном отражении её диаметр перейдет в сопряженный диаметр, который будет просто диаметром сопряженной гиперболы (см. рис.). Также. как наблюдается перпендикулярность сопряженных диаметров на окружности (на рис. слева), аналогичная ортогональность наблюдается для сопряженных диаметров гиперболы со взаимно перпендикулярными асимптотами (на рис. справа).

Вариации и обобщения

Понятие диаметра допускает естественные обобщения на некоторые другие геометрические объекты.

• Под диаметром конического сечения понимается прямая проходящая через середины двух параллельных хорд.
• Под диаметром метрического пространства понимается точная верхняя грань расстояний между парами его точек. В частности:
  • Диаметр графа — это максимальное из расстояний между парами его вершин. Расстояние между вершинами определяется как наименьшее число рёбер, которые необходимо пройти, чтобы добраться из одной вершины в другую. Иначе говоря, это расстояние между двумя вершинами графа, максимально удаленными друг от друга.
  • Диаметр геометрической фигуры — максимальное расстояние между точками этой фигуры.
  • Диаметром множества M{\displaystyle M}, лежащего в метрическом пространстве с метрикой ρ{\displaystyle \rho }, называется величина (supx,y∈Mρ(x,y)){\displaystyle (\sup _{x,y\in M}\rho (x,y))}. Например, диаметр n-размерного гиперкуба со стороной s равен

d=s⋅n{\displaystyle d=s\cdot {\sqrt {n}}}.

Некоторые окружности, построенные в треугольнике на одном отрезке, как на диаметре

См. также

Литература

wiki.sc

формула и пояснения :: SYL.ru

Нас окружает множество предметов. И многие из них имеют круглую форму. Она задана им для удобного использования. Взять, например, колесо. Если бы оно было изготовлено в форме квадрата, то как бы катилось по дороге?

Для того чтобы изготовить предмет круглой формы, нужно знать, как выглядит формула длины окружности через диаметр. Для этого сначала определим, что же представляет собой это понятие.

Круг и окружность

Окружностью является множество точек, которые размещены на равном расстоянии от основной точки — центра. Это расстояние называется радиусом.

Расстояние между двумя точками на данной линии называется хордой. Помимо того, если хорда проходит через основную точку (центр), тогда она называется диаметром.

А теперь рассмотрим, что такое круг. Совокупность всех точек, которые находятся внутри очертания, называется кругом.

После того как мы рассмотрели все определения, мы можем высчитывать диаметр окружности. Формула будет рассмотрена немного позже.

Для начала мы попробуем измерить длину очертания стакана. Для этого мы обмотаем его ниткой, затем ее измерим линейкой и узнаем приблизительную длину воображаемой линии вокруг стакана. Потому что размер зависит от правильного измерения предмета, а данный способ не является надежным. Но тем не менее сделать точные измерения вполне возможно.

Для этого опять вспомним о колесе. Неоднократно мы видели, что если увеличить спицу в колесе (радиус), то увеличится и длина обода колеса (окружности). И так же при уменьшении радиуса окружности уменьшается и длина обода.

Если внимательно проследить за этими изменениями, то увидим, что длина воображаемой круглой линии пропорциональна ее радиусу. И данное число является постоянным. Дальше рассмотрим, как определяется диаметр окружности: формула для этого применится в примере ниже. И рассмотрим ее, следуя шаг за шагом.

Формула окружности через диаметр

Поскольку длина очертания пропорциональна к радиусу, то и соответственно пропорциональна диаметру. Поэтому ее длину мы условно означим буквой C, диаметр — d. Поскольку соотношение длины очертания и диаметра — постоянное число, то его можно определить.

Проделав все подсчеты, мы определим число, которое приблизительно равно 3,1415… По той причине, что при подсчетах конкретное число не получилось, то обозначим его буквой π. Этот значок нам пригодится для того, чтобы была выведена формула длины окружности через диаметр.

Проведем воображаемую линию через центральную точку и измерим расстояние между двумя крайними. Это и будет диаметр. Если будем знать диаметр окружности, формула для определения длины ее самой будет выглядеть так: C = d * π.

Если мы будем определять длину разных очертаний, то если известен их диаметр, формула будет применена одна и та же. Поскольку знак π — это приблизительное исчисление, то и было решено умножать диаметр на 3,14 (число, округленное до сотых).

Как вычислить диаметр: формула

На этот раз попробуем с помощью данной формулы вычислить другие величины, помимо длины очертания. Чтобы вычислить диаметр по длине окружности, формула используется та же. Только для этого ее длину делим на π. Это будет выглядеть так d = C / π.

Рассмотрим, как эта формула действует на практике. К примеру, нам известна длина очертания колодца, следует вычислить его диаметр. Измерить его невозможно, поскольку из-за погодных условий нет доступа к нему. А задача у нас — изготовить крышку. Что будем делать в таком случае?

Нужно воспользоваться формулой. Возьмем длину очертания колодца — к примеру, 600 см. В формулу ставим конкретное число, а именно С = 600 / 3,14. В результате мы получим приблизительно 191 см. Округлим результат до 200 см. Затем с помощью циркуля рисуем круглую линию с радиусом в 100 см.

Поскольку очертание с большим диаметром нужно чертить соответствующим циркулем, то такой инструмент можно изготовить самому. Для этого возьмем рейку нужной длины и на каждом конце вбиваем по гвоздю. Устанавливаем один гвоздь в заготовку и слегка его вбиваем, для того чтобы он не сдвинулся с намеченного места. А с помощью второго чертим линию. Приспособление очень простое и удобное.

Современные технологии позволяют для вычисления длины очертания использовать онлайн-калькулятор. Для этого нужно всего лишь ввести диаметр окружности. Формула будет применена автоматически. Так же можно вычислять длину окружности с помощью радиуса. Кроме того, если вы знаете длину окружности, онлайн-калькулятор вычисляет радиус и диаметр с помощью данной формулы.

www.syl.ru

Формула длины окружности через радиус или диаметр

Окружность это замкнутая кривая линия, все точки которой, равноудалены от другой, определенной точки (центр окружности) на заданном расстоянии (радиус).
Радиус окружности — отрезок, соединяющий её центр и любую другую точку расположенную на линии окружности.
Диаметр окружности — отрезок, соединяющий две любые точки расположенные на линии окружности и проходящий через её центр. Диаметр, в два раза больше радиуса

---

r — радиус окружности

D — диаметр окружности

π ≈ 3.14

 

Формула длины окружности через радиус или диаметр, (L):

 

---

Калькулятор для расчета длины окружности через радиус

---

---

Калькулятор для расчета длины окружности через диаметр

---

 

S — площадь круга

O — центр круга

π ≈ 3.14

 

Формула длины окружности через площадь, (L):

 

---

Калькулятор для расчета длины окружности через площадь

---

 

Формулы для окружности и круга:

Подробности

Автор: Сергей Кондратов

Опубликовано: 07 сентября 2011

Обновлено: 09 октября 2017

www-formula.ru

Как вычислить диаметр окружности?

Для начала, давайте разберемся, что такое окружность и в чем ее отличие от круга. Возьмите ручку или карандаш красного цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, – это окружность. А вот синее содержимое внутри нее — и есть круг.

Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

D = 2 * R

К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить длину окружности. Формула L = 2 Пи * R, где 2 – это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

L = Пи * D

D = L / Пи

Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

D = 7 / 3, 14

D = 21, 98

Ответ: диаметр равен 21,98 метрам.

Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

D = 2 * (S / Пи) * (1 / 2)

S – в данном случае площадь фигуры. Допустим, в задаче она равна 30 кв. м. Получаем:

D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

R = S / p (S – площадь заданного треугольника, а p – периметр, разделенный на 2).

Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

Нередко находить диаметр окружности приходится и в быту. К примеру, при определении размера кольца, что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

fb.ru

Как определить диаметр окружности | Сделай все сам

Окружность – замкнутая кривая, точки которой равноудалены от ее центра. Основными колляциями окружности являются радиус и диаметр , связанные между собой как визуально, так и арифметически.

Инструкция

1. Диаметр – это отрезок, соединяющий две произвольные точки на окружности и проходящий через ее центр. Следственно, если диаметр надобно обнаружить, зная радиус данной окружности , то следует умножить численное значение радиуса на два, и измерить обнаруженное значение в тех же единицах, что и радиус. Пример: Радиус окружности 4 сантиметра. Обнаружить диаметр этой окружности . Решение: Диаметр равен 4 см*2=8 см. Результат: 8 сантиметров.

2. Если диметр надобно обнаружить через длину окружности , то делать необходимо применяя шаг 1-й. Существует формула для расчета длины окружности : l=2пR, где l-длина окружности , 2- константа, п – число, равное 3,14; R – радиус окружности . Зная, что диаметр – это двойственный радиус, вышеуказанную формулу дозволено записать в виде: l=пD, где D – диаметр .

3. Выразить из данной формулы диаметр окружности : D=l/п. И подставить в нее все вестимые величины, вычислив линейное уравнение с одним незнакомым. Пример: Обнаружить диаметр окружности , если ее длина составляет 3 метра. Решение: диаметр равен 3/3 = 1м. Результат: диаметр равен одному метру.

Окружность представляет собой фигуру плоскости, чьи точки идентично удалены от ее центра, а диаметр окружности – отрезок, проходящий через данный центр и соединяющий две самые удаленные точки окружности. Именно диаметр часто становится той величиной, которая разрешает решить множество задач в геометрии по нахождению окружности.

Инструкция

1. Скажем, дабы обнаружить длину окружности, довольно определить в виде начальных данных знаменитый диаметр . Задайте, что вам знаменит диаметр окружности, равный N, и начертите в соответствии с этими данными окружность. От того что диаметр соединяет две точки окружности и проходит при этом через центр, следственно, радиус окружности неизменно будет равен значению половинного диаметр а, то есть r = N/2.

2. Используйте для нахождения длины либо всякий иной величины математическую константу ?. Она представляет собой отношение значения длины окружности к значению длины диаметр а окружности и в геометрических вычислениях принимается равной ? ? 3,14.

3. Дабы определить длину окружности, возьмите стандартную формулу L = ?*D и подставьте значение диаметр а D = N. В итоге диаметр , умноженный на величину 3.14, покажет примерную длину окружности.

4. В случае когда требуется определить не только длину окружности, но и ее площадь, также воспользуйтесь значением константы ?. Только в данный раз воспользуйтесь иной формулой, согласно которой площадь круга определяется как длина радиуса, возведенная квадрат, и умноженная на число ?. Соответственно формула выглядит дальнейшим образом: S = ?*(r^2).

5. От того что в начальных данных определено, что радиус r = N/2, следственно, формула площади окружности видоизменяется: S = ?*(r^2) = ?*((N/2)^2). В итоге, если вы подставите в формулу значение знаменитого диаметр а, вы получите желанную площадь.

6. Не позабудьте проверить, в каких единицах измерения нужно определить длину либо площадь окружности. Если в начальных данных определено, что диаметр измеряется в миллиметрах, площадь круга также должна измеряться в миллиметрах. Для других единиц – см2 либо м2 расчеты производятся подобно.

Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это обозначает, что первую из них дозволено перевести во вторую без каких-нибудь дополнительных данных. Математической константой, через которую они связаны между собой, является число ?.

Инструкция

1. Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить примерно, измерьте его непринужденно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, обнаружьте его при помощи циркуля. Для этого используйте угольник с углами в 90 и 45 градусов. Приложите его 90-градусным углом к окружности таким образом, дабы ее касались оба катета, и обведите. Приложив после этого к получившемуся прямому углу 45-градусный угол угольника, начертите биссектрису. Она пройдет через центр окружности. После этого аналогичным образом начертите в ином месте окружности 2-й прямой угол и его биссектрису. Они пересекутся в центре. Это дозволит измерить диаметр.

2. Для измерения диаметра предпочтительно применять линейку, изготовленную из как дозволено больше тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а после этого, не изменяя его раствора, перенесите его на миллиметровую бумагу.

3. Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа дозволено измерить длину окружности при помощи курвиметра, а диаметр после этого рассчитать. Дабы воспользоваться курвиметром, сначала вращением его колесика установите стрелку верно на нулевое деление. После этого подметьте на окружности точку и прижмите курвиметр к листу таким образом, дабы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих вновь не окажется над этой точкой. Прочитайте показания. Они будут в сантиметрах – при необходимости переведите их в миллиметры.

4. Зная длину окружности (указанную в условиях задачи либо измеренную курвиметром), поделите ее на удвоенное число ?. Получится диаметр, выраженный в тех же единицах измерения, что и начальные данные. Если это требуется условиями, переведите итог вычисления в другие, больше комфортные единицы.

Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка – центр окружности, а отрезок между точкой на косой и ее центром именуется радиусом окружности.

Инструкция

1. Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью именуется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиусокружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.

2. Начертите несколько окружностей различным раствором циркуля. Визуальное сопоставление дозволяет сделать итог, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следственно, между диаметром окружности и ее длиной существует прямо пропорциональная связанность.

3. По физическому смыслу параметр «длина окружности» соответствует периметру многоугольника, ограниченного ломаной линией. Если вписать в окружность верный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (?/n), где R — радиус окружности, в которую вписали n-угольник.

4. При увеличении числа сторон периметр вписанного многоугольника будет все огромнее приближаться к длине окружности L. Р= b*n=2n*R*Sin (?/n)=n*D*Sin (?/n). Связанность между длиной окружности L и ее диаметром D непрерывна. Отношение L/D=n*Sin (?/n) при тяготении числа сторон вписанного многоугольника к бесконечности тяготится к числу ?, непрерывной величине, называемой «число пи» и выраженной безмерной десятичной дробью. Для расчетов без использования вычислительной техники принимается значение ?=3,14. Длина окружности и ее диаметр связаны формулой: L= ?D. Для вычисления диаметра окружности поделите ее длину на число ?=3,14.

Видео по теме

Полезный совет
В математических задачах зачастую разрешается применять число “пи” как легко 3, а 3,14.

jprosto.ru