| Символ (TeX) (Команда (TeX)) | Символ (Юникод) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒{\displaystyle \Rightarrow } (\Rightarrow) →{\displaystyle \rightarrow } (\rightarrow) ⊃{\displaystyle \supset } (\supset) | ⇒ → ⊃ | Импликация, следование | A⇒B{\displaystyle A\Rightarrow B} означает «если A{\displaystyle A} верно, то B{\displaystyle B} также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒ или для обозначения надмножества, см. ниже.). | x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4} верно, но x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2} неверно (так как x=−2{\displaystyle x=-2} также является решением). |
| «влечёт» или «если…, то» или «отсюда следует» | ||||
| везде | ||||
| ⇔{\displaystyle \Leftrightarrow } (\Leftrightarrow) | ⇔ | Равносильность | A⇔B{\displaystyle A\Leftrightarrow B} означает «A{\displaystyle A} верно тогда и только тогда, когда B{\displaystyle B} верно». | x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y} |
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧{\displaystyle \wedge } (\wedge) | ∧ | Конъюнкция | A∧B{\displaystyle A\wedge B} истинно тогда и только тогда, когда A{\displaystyle A} и B{\displaystyle B} оба истинны. | (n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, если n{\displaystyle n} — натуральное число. |
| «и» | ||||
| Математическая логика | ||||
| ∨{\displaystyle \vee } (\vee) | ∨ | Дизъюнкция | A∨B{\displaystyle A\vee B} истинно, когда хотя бы одно из условий A{\displaystyle A} и B{\displaystyle B} истинно. | (n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, если n{\displaystyle n} — натуральное число. |
| «или» | ||||
| Математическая логика | ||||
| ¬{\displaystyle \neg } (\neg) | ¬ | Отрицание | ¬A{\displaystyle \neg A} истинно тогда и только тогда, когда ложно A{\displaystyle A}. | ¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)} |
| «не» | ||||
| Математическая логика | ||||
| ∀{\displaystyle \forall } (\forall) | ∀ | Квантор всеобщности | ∀x,P(x){\displaystyle \forall x,P\left(x\right)} обозначает «P(x){\displaystyle P\left(x\right)} верно для всех x{\displaystyle x}». | ∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n} |
| «Для любых», «Для всех», «Для всякого» | ||||
| Математическая логика | ||||
| ∃{\displaystyle \exists } (\exists) | ∃ | Квантор существования | ∃x,P(x){\displaystyle \exists x,\;P\left(x\right)} означает «существует хотя бы один x{\displaystyle x} такой, что верно P(x){\displaystyle P\left(x\right)}» | ∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (подходит число 5) |
| «существует» | ||||
| Математическая логика | ||||
| ={\displaystyle =} | = | Равенство | x=y{\displaystyle x=y} обозначает «x{\displaystyle x} и y{\displaystyle y} обозначают одно и то же значение». | 1 + 2 = 6 − 3 |
| «равно» | ||||
| везде | ||||
| :={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } | := :⇔
| Определение | x:=y{\displaystyle x:=y} означает «x{\displaystyle x} по определению равен y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означает «P{\displaystyle P} по определению равносильно Q{\displaystyle Q}» | ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}\left(x\right):={1 \over 2}\left(e^{x}+e^{-x}\right)} (определение гиперболического косинуса) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (определение исключающего «ИЛИ») |
| «равно/равносильно по определению» | ||||
| везде | ||||
| {,}{\displaystyle \{,\}} | { } | Множество элементов | {a,b,c}{\displaystyle \{a,\;b,\;c\}} означает множество, элементами которого являются a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}. | N={1,2,…}{\displaystyle \mathbb {N} =\{1,\;2,\;\ldots \}} (множество натуральных чисел) |
| «Множество…» | ||||
| Теория множеств | ||||
| {|}{\displaystyle \{|\}} | {|} | Множество элементов, удовлетворяющих условию | {x|P(x)}{\displaystyle \{x\,|\,P\left(x\right)\}} означает множество всех x{\displaystyle x} таких, что верно P(x){\displaystyle P\left(x\right)}. | {n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}} |
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅{\displaystyle \varnothing } (\varnothing) {}{\displaystyle \{\}} | ∅ {} | Пустое множество | {}{\displaystyle \{\}} и ∅{\displaystyle \varnothing } означают множество, не содержащее ни одного элемента. | {n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing } |
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈{\displaystyle \in } (\in) ∉{\displaystyle \notin } (\notin) | ∈ ∉ | Принадлежность/непринадлежность к множеству | a∈S{\displaystyle a\in S} означает «a{\displaystyle a} является элементом множества S{\displaystyle S}» a∉S{\displaystyle a\notin S} означает «a{\displaystyle a} не является элементом множества S{\displaystyle S}» | 2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} } |
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆{\displaystyle \subseteq } (\subseteq) ⊂{\displaystyle \subset } (\subset) | ⊆ ⊂ | Подмножество | A⊆B{\displaystyle A\subseteq B} означает «каждый элемент из A{\displaystyle A} также является элементом из B{\displaystyle B}». A⊂B{\displaystyle A\subset B} обычно означает то же, что и A⊆B{\displaystyle A\subseteq B}. Однако некоторые авторы используют ⊂{\displaystyle \subset }, чтобы показать строгое включение (то есть ⊊{\displaystyle \subsetneq }). | (A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} } |
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇{\displaystyle \supseteq } (\supseteq) ⊃{\displaystyle \supset } (\supset) | ⊇ ⊃ | Надмножество | A⊇B{\displaystyle A\supseteq B} означает «каждый элемент из B{\displaystyle B} также является элементом из A{\displaystyle A}». A⊃B{\displaystyle A\supset B} обычно означает то же, что и A⊇B{\displaystyle A\supseteq B}. Однако некоторые авторы используют ⊃{\displaystyle \supset }, чтобы показать строгое включение (то есть ⊋{\displaystyle \supsetneq }). | (A∪B)⊇A{\displaystyle (A\cup B)\supseteq A} R⊇Q{\displaystyle \mathbb {R} \supseteq \mathbb {Q} } |
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊{\displaystyle \subsetneq } (\subsetneq) | ⊊ | Собственное подмножество | A⊊B{\displaystyle A\subsetneq B} означает A⊆B{\displaystyle A\subseteq B} и A≠B{\displaystyle A\neq B}. | N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} } |
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋{\displaystyle \supsetneq } (\supsetneq) | ⊋ | Собственное надмножество | A⊋B{\displaystyle A\supsetneq B} означает A⊇B{\displaystyle A\supseteq B} и A≠B{\displaystyle A\neq B}. | Q⊋N{\displaystyle \mathbb {Q} \supsetneq \mathbb {N} } |
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪{\displaystyle \cup } (\cup) | ∪ | Объединение | A∪B{\displaystyle A\cup B} означает множество, содержащее все элементы из A{\displaystyle A} и B{\displaystyle B} | A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B} |
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ∩{\displaystyle \cap } (\cap) | ⋂ | Пересечение | A∩B{\displaystyle A\cap B} означает множество одинаковых элементов, принадлежащих и A{\displaystyle A}, и B{\displaystyle B}. | {x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}} |
| «Пересечение … и … «, «…, пересечённое с …» | ||||
| Теория множеств | ||||
| ∖{\displaystyle \setminus } (\setminus) | \ | Разность множеств | A∖B{\displaystyle A\setminus B} означает множество элементов, принадлежащих A{\displaystyle A}, но не принадлежащих B{\displaystyle B}. | {1,2,3,4}∖{3,4,5,6}={1,2}{\displaystyle \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\}=\{1,\;2\}} |
| «разность … и …», «минус», «… без …» | ||||
| Теория множеств | ||||
| →{\displaystyle \to } (\to) | → | Функция (отображение) | f:X→Y{\displaystyle f\colon X\to Y} означает функцию f{\displaystyle f} с областью определения X{\displaystyle X} и областью значений Y{\displaystyle Y}. | Функция f:Z→N∪{0}{\displaystyle f\colon \mathbb {Z} \to \mathbb {N} \cup \{0\}}, определённая как f(x)=x2{\displaystyle f\left(x\right)=x^{2}} |
| «из … в …», | ||||
| везде | ||||
| ↦{\displaystyle \mapsto } (\mapsto) | ↦ | Отображение | f:x↦f(x){\displaystyle f\colon x\mapsto f\left(x\right)} означает, что образом x{\displaystyle x} после применения функции f{\displaystyle f} будет f(x){\displaystyle f\left(x\right)}. | Функцию, определённую как |
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | |||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
| Символ | Значение и происхождение |
|---|---|
| A{\displaystyle A} | Площадь (лат. area), векторный потенциал[1], работа (нем. Arbeit), амплитуда (лат. amplitudo), параметр вырождения, Работа выхода (нем. Austrittsarbeit), коэффициент Эйнштейна для спонтанного излучения, массовое число |
| a{\displaystyle a} | Ускорение (лат. acceleratio), амплитуда (лат. amplitudo), активность (лат. activitas), коэффициент температуропроводности, вращательная способность, радиус Бора, натуральный показатель поглощения света |
| B{\displaystyle B} | Вектор магнитной индукции[1], барионный заряд (англ. baryon number), удельная газовая постоянная, вириальний коэффициент, функция Бриллюэна (англ. Brillion function), ширина интерференционной полосы (нем. Breite), яркость, постоянная Керра, коэффициент Эйнштейна для вынужденного излучения, коэффициент Эйнштейна для поглощения, вращательная постоянная молекулы |
| b{\displaystyle b} | Вектор магнитной индукции[1], красивый кварк (англ. beauty/bottom quark), постоянная Вина, ширина распада (нем. Breite) |
| C{\displaystyle C} | Электрическая ёмкость (англ. capacitance), теплоёмкость (англ. heatcapacity), постоянная интегрирования (лат. constans), очарование (чарм, шарм; англ. charm), коэффициенты Клебша — Гордана (англ. Clebsch-Gordan coefficients), постоянная Коттона — Мутона (англ. Cotton-Mouton constant), кривизна (лат. curvatura) |
| c{\displaystyle c} | Скорость света (лат. celeritas), скорость звука (лат. celeritas), Теплоёмкость (англ. heat capacity), очарованный кварк (англ. charm quark), концентрация (англ. concentration), первая радиационная постоянная, вторая радиационная постоянная |
| D{\displaystyle D} | Вектор электрической индукции[1] (англ. electric displacement field), Коэффициент диффузии (англ. diffusion coefficient), Оптическая сила (англ. dioptric power), коэффициент прохождения, тензор квадрупольного электрического момента, угловая дисперсия спектрального прибора, линейная дисперсия спектрального прибора, коэффициент прозрачности потенциального барьера, D-мезон (англ. D meson), Диаметр (лат. diametros, др.-греч. διάμετρος) |
| d{\displaystyle d} | Расстояние (лат. distantia), Диаметр (лат. diametros, др.-греч. διάμετρος), дифференциал (лат. differentia), нижний кварк (англ. down quark), дипольный момент (англ. dipole moment), период дифракционной решётки, толщина (нем. Dicke) |
| E{\displaystyle E} | Энергия (лат. energīa), напряжённость электрического поля[1] (англ. electric field), Электродвижущая сила (англ. electromotive force), магнитодвижущая сила, освещенность (фр. éclairement lumineux), излучательная способность тела, модуль Юнга |
| e{\displaystyle e} | Основание натуральных логарифмов (2,71828…), электрон (англ. electron), элементарный электрический заряд (англ. elementaty electric charge), константа электромагнитного взаимодействия |
| F{\displaystyle F} | Сила (лат. fortis), постоянная Фарадея (англ. Faraday constant), свободная энергия Гельмгольца (нем. freie Energie), атомный фактор рассеяния, тензор электромагнитного поля, магнитодвижущая сила, модуль сдвига, фокусное расстояние (англ. focal length) |
| f{\displaystyle f} | Частота (лат. frequentia), функция (лат. functia), летучесть (нем. Flüchtigkeit), сила (лат. fortis), фокусное расстояние (англ. focal length), сила осциллятора, коэффициент трения |
| G{\displaystyle G} | Гравитационная постоянная (англ. gravitational constant), тензор Эйнштейна, свободная энергия Гиббса (англ. Gibbs free energy), метрика пространства-времени, вириал, парциальная мольная величина, поверхностная активность адсорбата, модуль сдвига, полный импульс поля, Глюон (англ. gluon), константа Ферми, квант проводимости, электрическая проводимость, Вес (нем. Gewichtskraft) |
| g{\displaystyle g} | Ускорение свободного падения (англ. gravitational acceleration), Глюон (англ. gluon), фактор Ланде, фактор вырождения, весовая концентрация, Гравитон (англ. graviton), метрический тензор |
| H{\displaystyle H} | Напряжённость магнитного поля[1], эквивалентная доза, энтальпия (англ. heat contents или от греческой буквы «эта», H — ενθαλπος[2]), гамильтониан (англ. Hamiltonian), функция Ганкеля (англ. Hankel function), функция Хевисайда (англ. Heaviside step function), бозон Хиггса (англ. Higgs boson), экспозиция, полиномы Эрмита (англ. Hermite polynomials) |
| h{\displaystyle h} | Высота (нем. Höhe), постоянная Планка (нем. Hilfsgröße[3]), спиральность (англ. helicity) |
| I{\displaystyle I} | сила тока (фр. intensité de courant), интенсивность звука (лат. intēnsiō), интенсивность света (лат. intēnsiō), сила излучения, сила света, момент инерции, вектор намагниченности |
| i{\displaystyle i} | Мнимая единица (лат. imaginarius), единичный вектор (координатный орт) |
| J{\displaystyle J} | Плотность тока (также 4-вектор плотности тока), момент импульса, функция Бесселя, момент инерции, полярный момент инерции сечения, вращательное квантовое число, сила света, J/ψ-мезон |
| j{\displaystyle j} | Мнимая единица (в электротехнике и радиоэлектронике), плотность тока (также 4-вектор плотности тока), единичный вектор (координатный орт) |
| K{\displaystyle K} | Каона (англ. kaons), термодинамическая константа равновесия, коэффициент электронной теплопроводности металлов, модуль всестороннего сжатия, механический импульс, постоянная Джозефсона, кинетическая энергия |
| k{\displaystyle k} | Коэффициент (нем. Koeffizient), постоянная Больцмана, теплопроводность, волновое число, единичный вектор (координатный орт) |
| L{\displaystyle L} | Момент импульса, дальность полёта, удельная теплота парообразования и конденсации, индуктивность, функция Лагранжа (англ. Lagrangian), классическая функция Ланжевена (англ. Langevin function), число Лоренца (англ. Lorenz number), уровень звукового давления, полиномы Лагерра (англ. Laguerre polynomials), орбитальное квантовое число, энергетическая яркость, яркость (англ. luminance) |
| l{\displaystyle l} | Длина (англ. length), длина свободного пробега (англ. length), орбитальное квантовое число, радиационная длина |
| M{\displaystyle M} | Момент силы, масса (лат. massa, от др.-греч. μᾶζα, кусок теста), вектор намагниченности (англ. magnetization), крутящий момент, число Маха, взаимная индуктивность, магнитное квантовое число, молярная масса |
| m{\displaystyle m} | Масса, магнитное квантовое число (англ. magnetic quantum number), магнитный момент (англ. magnetic moment), эффективная масса, дефект массы, масса Планка |
| N{\displaystyle N} | Количество (лат. numerus), постоянная Авогадро, число Дебая, полная мощность излучения, увеличение оптического прибора, концентрация, мощность, сила нормальной реакции |
| n{\displaystyle n} | Показатель преломления, количество вещества, нормальный вектор, единичный вектор, нейтрон (англ. neutron), количество (англ. number), основное квантовое число, частота вращения, концентрация, показатель политропы, постоянная Лошмидта |
| O{\displaystyle O} | Начало координат (лат. origo) |
| P{\displaystyle P} | Мощность (лат. potestas), давление (лат. pressūra), полиномы Лежандра, вес (фр. poids), сила тяжести, вероятность (лат. probabilitas), поляризуемость, вероятность перехода, импульс (также 4-импульс, обобщённый импульс; лат. petere) |
| p{\displaystyle p} | Импульс (также 4-импульс, обобщённый импульс; лат. petere), протон (англ. proton), дипольный момент, волновой параметр, давление, число полюсов, плотность. |
| Q{\displaystyle Q} | Электрический заряд (англ. quantity of electricity), количество теплоты (англ. quantity of heat), объёмный расход, обобщённая сила, хладопроизводительность, энергия излучения, световая энергия, добротность (англ. quality factor), нулевой инвариант Аббе, квадрупольный электрический момент (англ. quadrupole moment), энергия ядерной реакции |
| q{\displaystyle q} | Электрический заряд, обобщённая координата, количество теплоты (англ. quantity of heat), эффективный заряд, добротность |
| R{\displaystyle R} | Электрическое сопротивление (англ. resistance), универсальная газовая постоянная, постоянная Ридберга (англ. R ydberg constant), постоянная фон Клитцинга, коэффициент отражения, сопротивление излучения (англ. resistance), разрешение (англ. resolution), светимость, пробег частицы, расстояние |
| r{\displaystyle r} | Радиус (лат. radius), радиус-вектор, радиальная полярная координата, удельная теплота фазового перехода, удельная рефракция (лат. rēfractiō), расстояние |
| S{\displaystyle S} | Площадь поверхности (англ. surface area), энтропия[4], действие, спин (англ. spin), спиновое квантовое число (англ. spin quantum number), странность (англ. strangeness), главная функция Гамильтона, матрица рассеяния (англ. scattering matrix), оператор эволюции, вектор Пойнтинга |
| s{\displaystyle s} | Перемещение (итал. spostamento), странный кварк (англ. strange quark), путь, пространственно-временной интервал (англ. spacetime interval), оптическая длина пути |
| T{\displaystyle T} | Температура (лат. temperātūra), период (лат. tempus), кинетическая энергия, критическая температура, терм, период полураспада, критическая энергия, изоспин |
| t{\displaystyle t} | Время (лат. tempus), истинный кварк (англ. true quark), правдивость (англ. truth), планковское время |
| U{\displaystyle U} | Внутренняя энергия, потенциальная энергия, вектор Умова, потенциал Леннард-Джонса, потенциал Морзе, 4-скорость, электрическое напряжение |
| u{\displaystyle u} | Верхний кварк (англ. up quark), скорость, подвижность, удельная внутренняя энергия, групповая скорость |
| V{\displaystyle V} | Объём (фр. volume), электрическое напряжение (англ. voltage), потенциальная энергия, видность полосы интерференции, постоянная Верде (англ. Verdet constant) |
| v{\displaystyle v} | Скорость (лат. vēlōcitās), фазовая скорость, удельный объём |
| W{\displaystyle W} | Механическая работа (англ. work), работа выхода, W-бозон, энергия, энергия связи атомного ядра, мощность |
| w{\displaystyle w} | Скорость, плотность энергии, коэффициент внутренней конверсии, ускорение |
| X |
Символ | Название | Объяснение | Примеры | Значение Unicode | Название в HTML | Символ LaTeX |
|---|---|---|---|---|---|---|
| Читается как | ||||||
| Категория | ||||||
| Импликация | A ⇒ B верно, только когда либо A ложно, либо B истинно. → может означать то же самое, что и ⇒ (символ может также указывать область определения и область значений функции, см. таблицу математических символов). ⊃ может означать то же самое, что и ⇒ (символ может также обозначать надмножество). | x = 2 ⇒ x2 = 4 истинно, но x2 = 4 ⇒ x = 2, в общем случае, ложно (поскольку x может быть равен −2). | U+21D2 U+2192 U+2283 | ⇒ → ⊃ | ⇒{\displaystyle \Rightarrow }\Rightarrow →{\displaystyle \to }\to ⊃{\displaystyle \supset }\supset ⟹{\displaystyle \implies }\implies | |
| из .. следует; если .. то | ||||||
| логика высказываний, алгебра Гейтинга[en] | ||||||
| Тогда и только тогда | A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны. | x + 5 = y + 2 ⇔ x + 3 = y | U+21D4 U+2261 U+2194 | ⇔ ≡ ↔ | ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow ≡{\displaystyle \equiv }\equiv ↔{\displaystyle \leftrightarrow }\leftrightarrow ⟺{\displaystyle \iff }\iff | |
| тогда и только тогда | ||||||
| логика высказываний | ||||||
| отрицание | Утверждение ¬A истинно тогда и только тогда, когда A ложно. Знак /, расположенный поверх другого оператора, означает то же самое, что «¬», помещённое перед выражением. | ¬(¬A) ⇔ A x ≠ y ⇔ ¬(x = y) | U+00AC U+02DC | ¬ ˜ ~ | ¬{\displaystyle \neg }\lnot или \neg ∼{\displaystyle \sim }\sim | |
| not (не) | ||||||
| логика высказываний | ||||||
| конъюнкция | Утверждение A ∧ B истинно, если и A, и B истинны, и ложно в противном случае. | n < 4 ∧ n >2 ⇔ n = 3, если n — натуральное число. | U+2227 U+0026 | ∧ & | ∧{\displaystyle \wedge }\wedge или \land \&[2] | |
| and (и) | ||||||
| логика высказываний, Булева алгебра | ||||||
| логическая дизъюнкция | Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны, утверждение неверно. | n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 когда n является натуральным числом. | U+2228 | ∨ | ∨{\displaystyle \lor }\lor или \vee | |
| or (или) | ||||||
| логика высказываний, Булева алгебра | ||||||
| исключающее или | Утверждение A ⊕ B верно, когда либо A, либо B верно, но не оба. A ⊻ B означает то же самое. | (¬A) ⊕ A всегда верно, A ⊕ A всегда неверно. | U+2295 U+22BB | ⊕ | ⊕{\displaystyle \oplus }\oplus ⊻{\displaystyle \veebar }\veebar | |
| xor | ||||||
| логика высказываний, Булева алгебра | ||||||
| Тавтология | Утверждение ⊤ безусловно верно. | A ⇒ ⊤ всегда верно. | U+22A4 | T | ⊤{\displaystyle \top }\top | |
| верх | ||||||
| логика высказываний, Булева алгебра | ||||||
| Противоречие | Утверждение ⊥ безусловно неверно. | ⊥ ⇒ A всегда верно. | U+22A5 | ⊥ F | ⊥{\displaystyle \bot }\bot | |
| ложь, неверно, ошибочно | ||||||
| логика высказываний, Булева алгебра | ||||||
| Квантор всеобщности | ∀ x: P(x) или (x) P(x) означает P(x) верно для всех x. | ∀ n ∈ ℕ: n2 ≥ n. | U+2200 | ∀ | ∀{\displaystyle \forall }\forall | |
| для любого; для всех | ||||||
| Логика первого порядка | ||||||
∃ | Квантор существования | ∃ x: P(x) означает, что существует по меньшей мере один x, такой, что P(x) верно. | ∃ n ∈ ℕ: n чётно. | U+2203 | ∃ | ∃{\displaystyle \exists }\exists |
| существует | ||||||
| логика первого порядка | ||||||
∃! | Единственность | ∃! x: P(x) означает, что существует ровно один x, такой, что P(x) верно. | ∃! n ∈ ℕ: n + 5 = 2n. | U+2203 U+0021 | ∃ ! | ∃!{\displaystyle \exists !}\exists ! |
| существует в точности один | ||||||
| логика первого порядка | ||||||
| Определение | x := y илиx ≡ y означает, что x является другим обозначением для y (но заметьте, что ≡ может означать и другое, как, например, конгруэнтность). P :⇔ Q означает, что P логически эквивалентно Q. | cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B) | U+2254 (U+003A U+003D) U+2261 U+003A U+229C | := : ≡ ⇔ | :={\displaystyle :=}:= ≡{\displaystyle \equiv }\equiv ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow | |
| определяется как | ||||||
| везде | ||||||
() | приоритетная группировка | Операции внутри скобок выполняются первыми. | (8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4. | U+0028 U+0029 | () | ( ){\displaystyle (~)} () |
| скобки | ||||||
| везде | ||||||
⊢ | Выводимо[en] | x ⊢ y означает, что y выводимо из x (в некоторых формальных системах). | A → B ⊢ ¬B → ¬A | U+22A2 | ⊢ | ⊢{\displaystyle \vdash }\vdash |
| выводимо | ||||||
| логика высказываний, логика первого порядка | ||||||
⊨ | Модель[en] | x ⊨ y означает, что x семантически влечёт за собой y | A → B ⊨ ¬B → ¬A | U+22A8 | ⊨ | ⊨{\displaystyle \vDash }\vDash |
| влечёт | ||||||
| логика высказываний, логика первого порядка |
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Алфавиты, номиналы, единицы / / Алфавиты, в т.ч. греческий и латинский. Символы. Коды. Альфа, бета, гамма, дельта, эпсилон… / / Таблица научных, математических, физических символов и сокращений. Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. Поделиться:
| ||||
ОБОЗНАЧЕНИЕ — это… Что такое ОБОЗНАЧЕНИЕ?
Обозначение — сопряжения, контролируемого размера, поверхности или зоны контроля, номер сварного шва или обозначение пересечения сварных швов, указываемого номерами сварных швов, через тире, например № 1 2, и других параметров. Источник … Словарь-справочник терминов нормативно-технической документации
обозначение — индикатор, указатель, помета, знак, символ, отметка, ярлык, название, указание, наименование, маркировка; выражение, артикул, вырисовывание, отбивка, намечание, определение, очерчивание, позиционирование, помечание, прорисовывание, наметка,… … Словарь синонимов
Обозначение — Действие по глаголу обозначить/обозначать Знак/Символ/Образ предмета или явления … Википедия
ОБОЗНАЧЕНИЕ — ОБОЗНАЧЕНИЕ, я, ср. 1. см. обозначить. 2. Знак, к рым что н. обозначено. Условные обозначения. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
ОБОЗНАЧЕНИЕ — ОБОЗНАЧЕНИЕ. Кодирование (наименование) средствами языка компонентов внеязыковых ситуаций, предметов и объектов. См. также номинация … Новый словарь методических терминов и понятий (теория и практика обучения языкам)
обозначение — ОБОЗНАЧЕНИЕ1, означение, отметка, спец. маркирование, спец. маркировка ОТМЕТКА, заметка, метка, помета, пометка ОБОЗНАЧАТЬ/ОБОЗНАЧИТЬ, замечать/заметить, намечать/наметить, означать/ означить, отмечать/отметить, спец., несов. и сов.… … Словарь-тезаурус синонимов русской речи
обозначение — Данный термин включает в себя товарные знаки, коммерческие обозначения, фирменные наименования, элементы дизайна, эмблемы и иные средства маркировки товаров/услуг, способные идентифицировать товары/услуги, а также их производителей. [Департамент… … Справочник технического переводчика
Обозначение — Обозначение ♦ Designation Отношение знака к его референту, т. е. к реальному или воображаемому объекту, находящемуся вне знака (в лингвистике употребляются также термины денотация или референция). Не путать со значением – внутренне присущим… … Философский словарь Спонвиля
обозначение — заявить обозначение • вербализация … Глагольной сочетаемости непредметных имён
обозначение — ОБОЗНАЧЕНИЕ, я, ср Знак, обозначающий что л.; Син.: знак. Тире в сложном предложении это чаще всего обозначение результата … Толковый словарь русских существительных
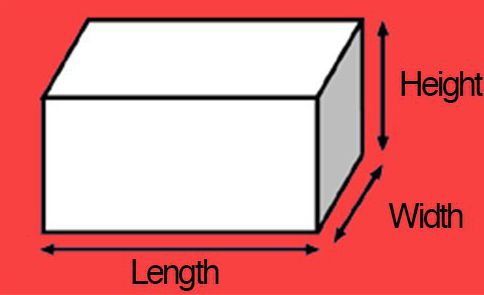
Обозначение: высота, ширина, длина. Ширина
Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.
Величины
Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.
Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.
Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.
Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.
Ширина
Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана. Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».
Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.
Длина
Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.
Высота
Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.
На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).
Радиус и диаметр
Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.
Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».
Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.
Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».
Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».
Толщина
Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.
Периметр и площадь
В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка. Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».
Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.
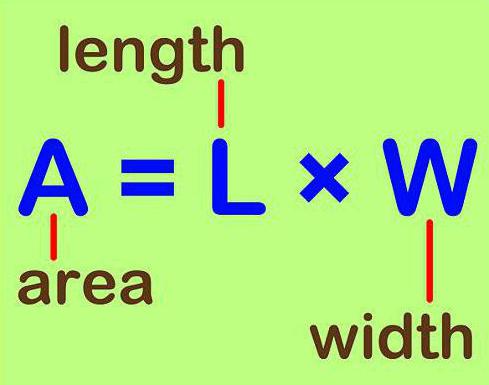Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).Другие распространенные сокращения
Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.
Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита. Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.
Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?
Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.