Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма. Площади плоских фигур. Формулы площади.

Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма.

Справочно: число пи

Пример 1

Прямоугольный поднос имеет длину 900 мм и ширину 350 мм. Определить его площадь в а) мм², б) в см², в) в м²

Решение:

а) Площадь =длина*ширина=900*350=315000 мм²

б) 1 см²=100 мм², следовательно,

315000 мм²=315000/100=3150 см²

1 м²=10000 см², следовательно,

3150 см²=3150/10000=0.315 м²

Пример 2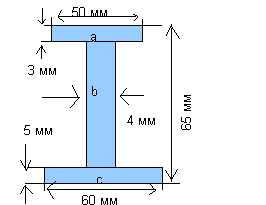

Определить площадь поперечного сечения балки, изображенной на рисунке.

Сечение балки можно разделить на три отдельных прямоугольника, как показано на рисунке

Sa=3*50=150 мм²

Sb=(65-5-3)*4=228 мм²

Sc=60*5=300 мм²

Общая площадь балки 150+228+300=678 мм²=6.78 см².

Пример 3

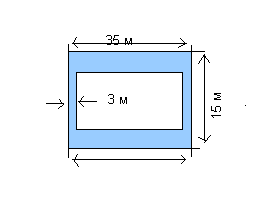
Определить площадь дорожки, показанной на рисунке.

Решение:

Площадь дорожки = площадь большого прямоугольника — площадь малого прямоугольника

S=35*15-29*11=206 м²

Пример 4

Определить площадь параллелограмма, показанного на рисунке (размеры приведены в миллиметрах).

Площадь параллелограмма = основание * высота. Высота h определяется по теореме Пифагора BC²=CE²+h²

Тогда

20²=(36-30)²+h²

h²=20²-6²=164

h=14,3 (приблизительно)

Следовательно, S_abcd=30*14.3=429 мм²

Пример 5

Показана боковая сторона здания. Определить площадь кирпичной кладки на боковой стороне.

Боковая сторона состоит из прямоугольника и треугольника.

S_прям.=6*10=60 м²

S _треуг. =1/2*основание*высота

CD=5 м, AD=6 м, следовательно, AC=3 м (по т. Пифагора). Следовательно,

S _треуг. =1/2*10*3=15 м².

Общая площадь кирпичной кладки есть 60+15=75 м²

Пример 6

Определить площади кругов, имеющих а) радиус 3 см, б) диаметр 10 мм, в) длину окружности 60 мм.

S=πr

2 или πd²/4.

а) S=πr²=π(3)²=9π=28.26 см²

б) S=πd²/4=π(10)²/4=100π/4=78.5 мм²

в) Длина окружности с=2πr, следовательно,

r=c/2π=60/2π=30/π

S=πr²=π(30/π)²=286.62 мм²

Пример 7

Вычислить площадь правильного восьмиугольника со стороной 5 см и поперечником 10 см.

Восьмиугольник — это многоугольник с 8 сторонами. Если из центра многоугольника провести лучи к вершинам, получится восемь одинаковых треугольников.

S _треуг. =1/2*основание*высота=1/2*5*10/2=12.5 см²

Площадь восьмиугольника есть 8*12.5=100 см²

 Пример 8

Определить площадь правильного шестиугольника со стороной 10 см.

Шестиугольник — это многоугольник с шестью сторонами, который может быть разбит на шесть равных треугольников, как показано на рис. сходящиеся в центре многоугольника углы треугольника равны 360^о/6=60^о

Другие два угла каждого треугольника составляют в сумме 120^о и равны между собой.

Следовательно, все треугольники являются равносторонними с углами 60^о и стороной 10 см

S _треуг. =1/2*основание*высота

Высоту h находим по теореме Пифагора:

10²=h²+5²

Отсюда h²=100-25=75

h=8.66 см

Следовательно, S _треуг. =1/2*10*8.66=43.3 см ²

Площадь шестиугольника равна 6*43.3=259.8 см²

Площадь поперечного сечения проводника: как найти площадь формулой

С необходимостью определения площади поперечного сечения проводника сталкивается каждый, кто хоть раз в жизни занимался ремонтом кабельной проводки в квартире, на даче, в гараже или офисе. Нехватка сечения может привести к пожару, так как провод будет сильно нагреваться. Если же сечение, наоборот, подобрано со значительным запасом, то стоимость проводки станет необоснованно высокой. В этой статье рассказывается, о различных методиках определения площади поперечного сечения проводника для круглых, одножильных, многожильных проводов и кабелей.

Что такое площадь поперечного сеченья

Если провод разрезать строго перпендикулярно его длине, чтобы металлические сердечники имели форму правильного круга, то несложно будет измерить диаметр этих жил и определить их площадь с использованием стандартной формулы.

Поперечное сечение

Важно! До недавнего времени опытные электрики могли определить этот параметр на глаз, но сегодня даже они вынуждены измерять провода, и проводить вычисления. Во времена Советского Союза все провода и кабели выпускались по единому ГОСТу, который и нормировал стандартные сечения. Если это 2.5 мм2, то электрик сразу мог отличить его от близких параметров 2 мм2 или 3 мм2. Сегодня производством кабельной продукции занимаются различные компании, которые могут сознательно уменьшать сечение провода и экономить на этом деньги. Вместо заявленных 2.5 мм2 в продажу может поступить провод 2,2 мм2, а это может иметь серьезные последствия и закончиться выгоранием проводки.

Чему равна площадь

Чему равна площадь поперечного сечения проводника – главный вопрос монтажника. Данный показатель является величиной, которая зависит от формы перпендикулярного среза геометрического тела. Проще всего определить площадь квадрата или прямоугольника, для чего достаточно перемножить между собой длину на ширину. Еще в Древней Греции научились рассчитывать площадь практически любой фигуры. Как правило, большинство проводов имеют круглую форму сечения, которую вычислить несложно по формуле или воспользовавшись справочной таблицей. Для этого нужно знать только диаметр или радиус жилы проводника.

Обратите внимание! Существуют кабели большого сечения, в составе которых расположены секторные провода. Но в конечном итоге, сердечники таких изделий рассчитываются исходя из общего приведённого диаметра всех металлических элементов в пучке. Для определения площади сечения каждой жилы необходимо общий показатель разделить на их количество в кабеле.

Секторный кабель

Чем измерять площадь

Для правильного измерения площади поперечного сечения важно сделать ровный перпендикулярный срез и измерить диаметр металла при помощи высокоточных приборов. В случае с многожильными проводами необходимо выполнить следующие шаги:

• Для точных расчетов нужна одиночная проволока. Из пучка проводов выделяют одну жилку и вычисляют площадь ее сечения.
• Пересчитывают количество жил в проводе.
• Перемножают площадь сечения жилки на их количество.

Полученный результат и будет искомой площадью многожильного проводника.

Многожильный провод

Дополнительная информация: Для вычисления площади сечения проводника необходимо, в первую очередь, измерить его диаметр, и сделать это лучше всего микрометром, штангенциркулем или, в крайнем случае, высокоточной инженерной линейкой. Так как микрометр – редкость в наборе инструментов электрика, то этот способ мы упустим и остановимся на штангенциркуле и линейке.

Штангенциркуль

Штангенциркуль — высокоточный измерительный инструмент, при помощи которого можно определить линейные размеры любого предмета, диаметры круглых изделий, а также глубину сквозных и глухих отверстий и выемок. Такой инструмент должен быть у каждого домашнего мастера, стоит он не дорого и при правильном обращении может прослужить не одно десятилетие.

Штангенциркуль

Штангенциркули подразделяются на следующие виды:

• Нониусные — имеют классическую конструкцию и высокоточную измерительную шкалу, которая позволяет измерять предметы с точностью до 0.1 – 0.05 мм.
• Со стрелочным отображением результатов измерений — очень удобный для снятия точных показаний инструмент, но его главным недостатком является повышенная хрупкость.
• С электронной индикацией результатов — относительно новая разработка, предназначенная для получения максимальной точности и удобного снятия показаний измерений.

Рассмотрим самый распространенный вид штангенциркуля — нониусный. Из таких инструментов наибольшее распространение получили два вида:

• ШЦ-I с точностью измерений 0,1 мм, такой инструмент есть практически у каждого слесаря.
• ШЦ-II с точностью измерений 0,05 мм, этот штангенциркуль предпочтительнее, так как в результате работы он выдаёт меньшую погрешность.

Для правильного измерения диаметра достаточно оголить сердечник кабеля путём снятия изоляция, после чего прижать раздвижные губки инструмента к его поверхности. Риска на подвижной части штангенциркуля совпадёт с показателем на шкале, который и будет являться диаметром.

Карандаш + линейка

Если под рукой нет точных измерительных инструментов, а определить диаметр провода необходимо в настоящий момент, можно воспользоваться старым проверенным способом. Картинка 5. Метод карандаша.

Для данного способа понадобятся круглый карандаш и линейка. Суть метода состоит в следующем алгоритме:

• Прежде всего необходимо отрезать кусок провода и очистить его от изоляции.
• Далее проволока из металлического сердечника плотно наматывается на карандаш, причём, минимальное количество витков должно быть не меньше 15. Здесь все зависит от толщины провода, и чем он тоньше, тем больше витков необходимо намотать.
• Проводятся вычисления по формуле, приведённой на картинке 6.

Формула расчета диаметра методом карандаша и линейки

Обратите внимание! Для получения точного результата следует наматывать провод на карандаш как можно плотнее. Для этого перед наматыванием его необходимо тщательно выровнять в местах перегибов и образования петель.

Как правильно найти площадь поперечного сечения (с помощью формулы)

Как найти площадь поперечного сечения проводника подскажет формула, известная из школьного курса геометрии – пr2. Когда известен диаметр провода, можно приступать к вычислению площади сечения. Сделать это несложно с помощью калькулятора по формуле, указанной на картинке 7.

Формула расчета площади

Таблица диаметров и сечения проводов

Формула для расчёта диаметра достаточно проста и выдаёт стандартные значения для конкретного диаметра. Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.

Таблица соотношений диаметров и площадей проводов

Таким способом можно пользоваться в том случае, если под рукой оказался стандартный проводник, указанный в ГОСТ. Например — при диаметре сердечника 2.8 мм площадь его сечения составит 6 мм2.

Прочитав эту статью, любой человек сможет самостоятельно рассчитать площадь поперечного сечения провода или кабеля. Это пригодится при замене старой проводки или при монтаже новой кабельной линии. Главное условия подбора – повышенная точность, так как идеального соотношения качества, простоты установки, безопасности и оптимальной цены можно добиться только после проведения кропотливых замеров.

Читать книгу Сопротивление материалов. Шпаргалка для студентов Романа Сиренко : онлайн чтение

22. Статический момент сечения

Расчеты на прочность показывают, что напряжение и деформации, возникающие в твердом теле, зависят от внутренних силовых факторов и геометрических характеристик поперечного сечения. При растяжении, например, напряжение зависит от площади поперечного сечения, и, так как напряжение в этом случае распределяется по сечению равномерно, не зависит от формы сечения. При кручении напряжения зависят от размеров и формы сечения из-за неравномерного распределения напряжений. В расчетные формулы бруса при кручении входят полярный момент инерции I_p и полярный момент сопротивления W_p – геометрические характеристики сечения. Проводя расчеты на прочность бруса при изгибе, необходимо знать моменты инерции и моменты сопротивления сечения относительно осей, проходящих через центр тяжести бруса. Возьмем для рассмотрения некоторое сечение бруса площадью A и ось, проходящую через центр тяжести этого тела. Статическим моментом плоского сечения относительно некоторой оси x называется сумма произведений площадей элементарных площадок, из которых состоит сечение, на расстояния этих площадок до оси, проходящей через центр тяжести. Аналогично для оси y.

Статический момент измеряется в кубических метрах. Он может быть положительным, отрицательным или равным нулю в зависимости от выбранной оси. Если известны статические моменты и площадь сечения, то координаты центра тяжести могут быть определены как отношение статического момента к площади поперечного сечения. И наоборот, если координаты центра тяжести сечения известны – x_c, y_c, статический момент равен произведению площади сечения на расстояния от центра тяжести до оси.

S_x = Ay_c

S_y = Ax_c

Из полученных соотношений видно, что в случае, когда ось проходит через центр тяжести, статический момент равен нулю.

В случае, когда сечение можно рассматривать как n-ное количество составляющих частей с известными площадями A_i и координатами центров тяжести x_i, y_i, положение всего центра тяжести можно определить как сумму произведений:

Каждое слагаемое в числителе определяет статический момент данного участка относительно выбранной оси.

23. Момент инерции сечения

Осевым (или экваториальным) моментом инерции плоского сечения относительно некоторой оси x называется сумма произведений площадей элементарных площадок, из которых состоит сечение на квадрат расстояния этих площадок до оси, проходящей через центр тяжести. Таким образом, осевые моменты представляют собой интегралы по всей площади сечения.

Полярным моментом инерции относительно некоторой точки (полюса) называется сумма произведений площадей элементарных площадок, из которых состоит сечение, на квадрат расстояния этих площадок до выбранной точки.

Центробежным моментом инерции относительно некоторых двух взаимно перпендикулярных осей называется сумма произведений элементарных площадок, из которых состоит сечение, на расстояния этих площадок до этих осей.

Моменты инерции измеряются в м⁴. Осевые и полярный моменты инерции могут быть только положительными, так как при любом знаке координаты в формуле берется квадрат этой координаты. Центробежный момент инерции может быть положительным, отрицательным и равным нулю.

Сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равна полярному моменту инерции относительно точки, где эти оси пересекаются.

I_ρ = I_x +I_y

Действительно, ρ – это расстояние от элементарной площадки сечения до некоторой точки, он определяется как гипотенуза треугольника со сторонами x и y.

ρ² = x² + y²

Подставим это соотношение в выражение для полярного момента инерции и получим:

24. Моменты инерции простых сечений

Рассмотрим моменты инерции некоторых простых фигур.

Круг. I_ρ = I_x +I_y. Так как круг – симметричная фигура, то I_x= I_y. Следовательно, I_ρ = 2I_x. Исходя из определения полярного момента инерции и соотношения для полярного момента инерции и осевых моментов инерции в случае круга имеем:

Для кольца диаметром d и внутренним диаметром d₀

Полукруг. Главные центральные оси представляют собой ось симметрии этого полукруга и перпендикулярную ей ось. Для полукруга момент инерции в два раза меньше, чем момент инерции круга для той же самой оси. Если обозначить x₁ ось основания, то

Из соотношения, связывающего моменты инерции параллельных осей, одна из которых является центральной, и, зная значение ординаты центра тяжести полукруга y_c ≈ 0.424r можно определить моменты инерции полукруга:

Прямоугольник. Определим момент инерции I_x1, совпадающий с основанием прямоугольника, и рассмотрим сечение A как сумму элементарных прямоугольников шириной b и высотой dy₁, A = bdy₁

Для моментов инерции параллельных осей, одна из которых является центральной, I_x = I_x1 – a²A. В данном случае расстояние a = h / 2, A = bh, момент инерции относительно осей x и y

I_x = bh³ / 12

I_y = hb³ / 12

В частном случае квадрата

I_x = I_y = b⁴ / 12

Для треугольника вычислим момент инерции I_x1, относительно оси x₁, совпадающей с основанием, и для этого рассмотрим сечение как сумму элементарных прямоугольников шириной b. После выполнения математических преобразований найдем значение I_x= bh³ / 12. Момент инерции относительно центральной оси равен I_x = I_x1 — a²b, в данном случае a = h / 3, A = (1 / 2)bh. В итоге получим:

I_x = bh³ / 12 – (h / 3)³(1 / 2)bh = bh³ / 36

В общем случае ось x не является главной и

I_y = bh³ / 48

25. Зависимость между моментами инерции относительно параллельных осей

Установим зависимость между моментами инерции относительно параллельных осей, одна из которых является центральной. Для этого рассмотрим сечение площадью А. (Рис. 10) Предположим, что известны координаты центра тяжести сечения C и моменты инерции I_xc, I_yc относительно центральных осей x_c, y_c. В таком случае можно определить моменты инерций относительно осей x и y, параллельных центральным и удаленным от центральных на расстояние a и b соответственно. Запишем соотношение для координат параллельных осей:

x = x_c + b

y = y_c + a

Тогда момент инерции сечения относительно оси x запишется в виде:

В этом выражении первое слагаемое представляет собой момент инерции относительно оси x_c, во втором слагаемом интеграл представляет статический момент (а относительно центральной оси статический момент всегда равен нулю), третье слагаемое – это площадь сечения, умноженная на квадрат расстояния между осями а. Таким образом:

I_x = I_xc + a²A

I_y = I_yc + b²A

Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллельной данной, и произведения площади сечения фигуры на квадрат расстояния между осями.

Мы получили соотношение для моментов инерции относительно центральных осей при переходе к параллельным им нецентральным. Эти соотношения носят также название формул параллельного переноса.

Из полученных формул понятно, что момент инерции относительно центральной оси всегда меньше, чем момент инерции любой параллельной ей нецентральной.

Рис. 10

26. Главные оси инерции и главные моменты инерции

Через любую точку плоскости сечения можно провести бесчисленное множество пар взаимно перпендикулярных осей. Так как сумма двух осевых моментов инерции сечения представляет собой полярный момент и является постоянной величиной, то, перемещая систему координат, можно подобрать такое положение осей, в котором один из выбранных моментов инерции будет максимальным, а второй – минимальным. Рассмотрим зависимость между моментами инерции относительно осей x₀, y₀ и моментами инерции относительно осей x и y, повернутыми на угол α относительно x₀, y₀. Найдем такие значения угла α, при которых моменты инерции перпендикулярных осей примут свои максимальное и минимальное значения. Для этого найдем первую производную по углу поворота от I_x, I_y и приравняем ее нулю (математическое правило нахождения экстремумов функции).

После преобразований соотношение примет вид:

Полученная формула определяет положение двух взаимно перпендикулярных осей, момент инерции относительно одной из которых максимален, момент инерции относительно другой минимален. Такие оси носят название главных осей инерции. Моменты инерции относительно таких осей называются главными моментами инерции. При этом центробежный момент равняется нулю.

Оси, проходящие через центр тяжести сечения, носят название центральных осей. В практических расчетах интерес представляют главные моменты инерции относительно центральных осей, их называют главными центральными моментами инерции, а такие оси – главными центральными осями. Так как интерес представляют только центральные оси, то для краткости их называют просто главными осями, и осевые моменты инерции, вычисленные относительно таких осей называют просто главными моментами инерции.

Одной из главных осей инерции является ось, проходящая через центр симметрии плоскости сечения, вторая – перпендикулярная ей. Ось симметрии и любая перпендикулярная ей образуют систему главных осей. Если сечение имеет несколько осей симметрии (например, круг, квадрат, равносторонний треугольник), то все центральные оси являются главными и все центральные моменты равны.

27. Вычисление моментов инерции сложных сечений

Для нахождения момента инерции сложного сечения площадью A сечение разбивают на простые A₁, A₂, … A_n, для которых моменты инерции находятся по готовым формулам или таблицам.

Момент инерции сложной фигуры находится как сумма моментов инерции, составляющих простых фигур.

I_x = I_x1 + I_x2 +… + I_xn

Момент инерции представляет собой интеграл по площади поверхности сечения,

для интеграла справедливо:

Следовательно, можно записать, что:

Другими словами, момент инерции составного сечения относительно некоторой оси складывается из моментов инерции составляющих этого сечения относительно той же самой оси.

При решении задач такого рода придерживаются следующего алгоритма. Находят центр тяжести плоского сечения и определяют главные центральные оси. Из таблиц или с помощью готовых формул вычисляют значения моментов инерции составляющих частей относительно собственных центральных осей, параллельных главным центральным осям сечения. При помощи формул параллельного переноса вычисляют значения моментов инерции составляющих частей сечения относительно главных осей сечения. Путем суммирования определяют значения главных центральных моментов инерции.

Это правило справедливо также для центробежного момента инерции.

28. Понятие о крутящем моменте

Кручение – это один из видов деформации бруса, при котором в поперечном сечении бруса возникает один внутренний силовой фактор, называемый крутящим моментом Мк. Такой вид деформации возникает, когда на брус действует пара сил, называемых скручивающими моментами М, приложенных перпендикулярно его продольной оси.

Нагруженный вращающими моментами брус называется валом. Сумма вращающих моментов, действующих на вал, равна нулю, если вал вращается равномерно. Вращающий момент можно определить по формуле, с условием, что известны передаваемая мощность P и угловая скорость w.

При известной частоте вращения вала угловая скорость может быть записана в виде

Следовательно, выражение для вращающего момента можно записать в виде:

В практических расчетах реальный объект заменяется расчетной схемой. Для упрощения задачи предполагается, что вращательные моменты сосредоточены в среднем сечении деталей, а не распределены по их поверхности. В сечении произвольного вала крутящий момент можно определить, используя метод сечений, когда вал мысленно рассекается плоскостью. Одну из частей отбрасывают и заменяют ее влияние крутящим моментом Мк, затем определяют его из уравнений равновесия. Числовое значение крутящего момента складывается из сумм вращающих моментов, находящихся по одну сторону сечения.

В поперечных сечениях бруса при кручении возникают только касательные напряжения, нормальные силы параллельны продольной оси бруса и их моменты равны нулю. Следовательно, можно сформулировать определение для крутящего момента таким образом: крутящий момент – это результирующий момент внутренних касательных сил, возникающих в поперечном сечении бруса относительно его продольной оси.

При расчетах на прочность в случае кручения бруса необходимо найти опасное сечение бруса. Если размеры поперечного сечения вдоль оси бруса неизменны, то опасными считаются сечения с максимальным крутящим моментом. Для нахождения опасных сечений строятся эпюры крутящих моментов (графики изменения крутящих моментов по длине бруса). При построении эпюров принято считать, что крутящий момент положителен, если его направление совпадает с направлением часовой стрелки, если смотреть на проведенное сечение. Это предположение условно, так как знак крутящего момента не имеет физического смысла.

29. Определение напряжений при кручении круглого вала

При изучении кручения валов имеют место следующие предположения:

– гипотеза плоских сечений: плоские поперечные сечения бруса после деформации также остаются плоскими и направленными по нормали к его оси, поворачиваясь на некоторый угол относительно этой оси;

– радиусы поперечных сечений не искривляются, и их длина остается постоянной;

– вдоль оси бруса расстояния между поперечными сечениями остаются постоянными.

Исходя из перечисленных предположений кручение круглого вала можно рассматривать как чистый сдвиг. Полученные на основе этих предположений формулы подтверждаются экспериментально.

Рассмотрим кручение участка бруса круглого сечения с радиусом r длиной dz. Один из концов будем считать неподвижно закрепленным.

Рис. 11

При повороте на угол a в поперечном сечении угол сдвига, лежащий на поверхности такого вала, определяется по формуле:

Отношение полного угла закручивания на участке вала к его длине называется относительным углом закручивания.

Мысленно выделим в рассматриваемом участке вала цилиндр с радиусом ρ, угол сдвига для поверхности этого цилиндра определяется аналогично:

Согласно закону Гука в случае сдвига касательные напряжения равны:

Таким образом, при кручении касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения, причем у центра тяжести касательные напряжения равны нулю. Приближаясь к поверхности вала, они принимают свои максимальные значения.

30. Вычисление моментов, передаваемых на вал

Рассмотрим кручение участка круглого вала диметром r и длиной dz. Выделим в нем цилиндр диаметра ρ. Так как кручение представляет собой чистый сдвиг, нормальные напряжения равны нулю, а касательные напряжения при повороте на угол α распределяются следующим образом:

Крутящий момент определяется как:

А – площадь сечения. Подставив в это выражение касательное напряжение и учитывая, что интеграл от радиуса по площади сечения представляет собой полярный момент инерции сечения , получим:

Подставив это выражение в формулу для касательных напряжений, получим:

Таким образом, касательные напряжения определяются как произведение крутящего момента и радиуса, отнесенное к полярному моменту сечения. Ясно, что для точек, удаленных от оси на одинаковые расстояния, касательные напряжения равны, максимальные значения напряжения имеют точки, расположенных на поверхности вала.

Здесь  – полярный момент сопротивления при кручении.

Для круглого сечения

Условие прочности при кручении выглядит следующим образом:

[τ] – максимально допускаемое касательное напряжение.

Эта формула позволяет также определять допускаемый крутящий момент или подбирать допустимый диаметр вала.

31, Деформация при кручении. Потенциальная энергия

В процессе кручения вращающие моменты поворачиваются вместе с сечением на какой-то угол и при этом совершают работу, которая так же, как и при других видах деформации, расходуется на создание в теле, подвергающемся деформации, определенного запаса потенциальной энергии и определяется по формуле:

Это соотношение следует из линейной зависимости крутящего момента М_к от угла поворота φ.

Рис. 12

При воздействии нагрузки крутящий момент постепенно нарастает, при этом в соответствии с законом Гука пропорционально увеличивается угол поворота. Работа, совершаемая крутящим моментом, равна потенциальной энергии деформации согласно закону сохранения энергии, следовательно,

Если в полученное соотношение подставить известную формулу для угла закручивания, то выражение примет вид:

При ступенчатом изменении крутящего момента или поперечного сечения бруса потенциальная энергия представляет собой сумму:

Если же крутящий или полярный моменты (или оба одновременно) непрерывно изменяются по длине участков бруса, то потенциальная энергия представляет интеграл по длине

32. Расчет винтовых цилиндрических пружин

В машиностроении и приборостроении широко используются винтовые пружины, которые могут иметь цилиндрическую, конусовидную или фасонную. Чаще всего применяются пружины цилиндрической формы, изготовленные из проволоки круглого поперечного сечения: пружины растяжения (изготавливаются без просветов между витками) и пружины сжатия (с просветом). Для упрощения расчета пружин на жесткость и прочность будем считать, что угол наклона витков настолько мал, что им можно пренебречь и считать сечение вдоль оси пружины поперечным для витка. Из условий равновесия для отсеченной части пружины ясно, что в сечении возникают два внутренних силовых фактора: поперечная сила Q_y = F и крутящий момент М_к = FD / 2, т. е. в сечении витка возникают только касательные напряжения. Будем считать, что касательные напряжения, связанные с поперечной силой, распределены по сечению равномерно, а касательные силы, связанные с наличием крутящего момента, распределены по линейному закону и достигают своих максимальных значений в крайних точках сечения. Наиболее напряженной окажется точка, расположенная ближе всего к оси пружины, напряжение для нее равно:

Отношение диаметра пружины к диаметру проволоки называют индексом пружины,

c_n = D / d

Если считать что напряжения в витке возникают только от кручения, и пренебречь вторым слагаемым, формула запишется в следующем виде:

Полученная формула приближенна из-за пренебрежения влиянием поперечной силы и из-за того, что не учтена кривизна витков. Введем поправочный коэффициент К, зависящий от индекса пружины и угла наклона витков. Тогда условие прочности примет вид:

При воздействии нагрузки пружина изменяет свою длину. Это изменение называется осадкой пружины λ. Определим, чему равна осадка, если витки испытывают только кручение. Согласно формуле Клапейрона работа внешних статических сил равна:

Потенциальная энергия деформации

В данном случае

где l – длина рассматриваемого участка пружины;

n – число витков.

Выполнив подстановку и математические преобразования, получим, что:

33. Перемещения и напряжения в винтовых пружинах

Винтовые пружины широко используются в машиностроении как амортизирующие устройства или устройства обратной подачи. Расчет винтовых пружин хорошо демонстрирует метод определения перемещений. Винтовые пружины подразделяются на пружины растяжения, сжатия и кручения. Пружины растяжения и сжатия нагружаются силами, действующими вдоль оси пружины, пружины кручения нагружаются моментами, расположенными в плоскости, перпендикулярной оси пружины.

Витую пружину можно рассматривать как пространственно изогнутый стержень с осью, имеющей винтовую форму. Форма пружины характеризуется следующими параметрами: диаметром пружины D, числом витков n, углом подъема θ и шагом пружины s, определяемым формулой:

s = πDtgθ

Обычно шаг пружины значительно меньше, чем πD, угол θ достаточно мал (меньше 5°).

Рассмотрим пружину растяжения-сжатия. Под воздействием внешней нагрузки Р в каждом поперечном сечении возникает результирующая внутренняя сила Р и момент М = РD / 2, лежащий в плоскости действия сил Р. На Рис. 13 изображены силы, действующие в поперечном сечении пружины.

Рис. 13

Проекции полной силы и момента относительно системы координат, связанной с сечением, описываются следующими соотношениями:

M_к = (PD / 2) × cosθ,

M_изг= (PD / 2) × sinθ,

Q = P × cosθ,

N = P × sinθ.

Предположим, что сила Р равна 1, тогда соотношения для сил и моментов примут вид:

M_к1 = (D / 2) × cosθ,

M_изг1 = (D / 2) × sinθ,

Q₁ = cosθ,

N₁ = sinθ.

Найдем осевое перемещение в пружине, пользуясь интегралом Мора. С учетом малости перемещений, вызванных нормальной и поперечными силами, а также осевого перемещения, в данном случае интеграл Мора запишется следующим образом:

где произведение в знаменателе представляет собой жесткость пружины на кручение;

l – длина рабочей части пружины;

l ≈ πDn

Вследствие малости угла наклона витков θ полагаем, что cos θ = 1, тогда

Напряжения в винтовых пружинах, работающих на сжатие-растяжение или кручение, определяются следующим образом:

Расчет прямоугольного сечения балки — Лекции и примеры решения задач технической механики

Задача

Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.

Соотношение сторон сечения h=2b (h – высота, b – ширина).

Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [σ]=160МПа.

Решение

Предыдущие пункты решения задачи:

1. Определение опорных реакций
2. Построение эпюр внутренних поперечных сил и изгибающих моментов
3. Расчет момента сопротивления сечения балки по условию прочности

Минимально необходимый расчетный момент сопротивления сечения балки составил

В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.

По справочнику находим формулу осевого момента сопротивления прямоугольного сечения

Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении

и запишем необходимое неравенство

откуда находим расчетную высоту прямоугольного сечения

Из заданного соотношения сторон определяем расчетную ширину сечения

Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.

При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).

По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.

Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.

После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.

Оценка экономичности сечений >
Построение эпюры нормальных напряжений >
Другие примеры решения задач >

Заказать решение

Рекомендуем:

• Скачать рамки А4 для учебных работ
• Учебные работы по всем предметам
• Скачать шрифты ГОСТ (чертежные)
• Миллиметровки А4 разного цвета

Золотой прямоугольник — Википедия

Материал из Википедии — свободной энциклопедии

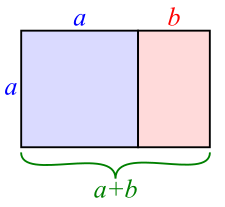Золотой прямоугольник с длинной стороной a и короткой b, помещённый рядом с квадратом со стороной a, даёт подобный золотой прямоугольник с длинной стороной a + b и короткой стороной a. Это иллюстрирует отношение a+ba=ab≡φ.{\displaystyle {\frac {a+b}{a}}={\frac {a}{b}}\equiv \varphi \,.}

Золотой прямоугольник — это прямоугольник, длины сторон которого находятся в золотой пропорции, 1:1+52{\displaystyle 1:{\tfrac {1+{\sqrt {5}}}{2}}}, или 1:φ{\displaystyle 1:\varphi } (греческая буква фи), где φ примерно равно 1,618.

Метод построения золотого прямоугольника. Квадрат выделен красным цветом. Результирующие размеры находятся в золотой пропорции.

Золотой прямоугольник можно построить с помощью циркуля и линейки следующим способом:

1. Строим обычный квадрат.
2. Из угла проводится линия до середины противоположной стороны.
3. Строим окружность, используя точку пересечения в качестве центра окружности, а в качестве радиуса используем полученный отрезок.
4. Продолжаем противоположную сторону до пересечения с окружностью.

Связь с правильными многоугольниками и многогранниками[править | править код]

Отличительной особенностью фигуры является то, что после удаления квадрата оставшаяся часть остаётся золотым прямоугольником, сохраняя то же самое отношение геометрических размеров^[en]. Удаление квадратов можно продолжать бесконечно, при этом соответствующие углы квадратов образуют бесконечную последовательность точек на золотой спирали, единственной логарифмической спирали с этим свойством.

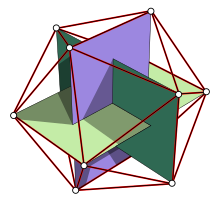Три золотых прямоугольника в икосаэдре

Другое построение золотого прямоугольника использует три правильных многоугольника, вписанных в одинаковые окружности — десятиугольник, шестиугольник и пятиугольник. Соответствующие длины сторон a, b и c этих трёх многоугольников удовлетворяют равенству a² + b² = c², так что отрезки с этими длинами образуют прямоугольный треугольник^[en] (согласно теореме Пифагора). Отношение длины стороны шестиугольника к длине стороны десятиугольника равно золотому сечению, так что треугольник образует половину золотого прямоугольника^[1].

Выпуклая оболочка двух противоположных рёбер правильного икосаэдра образует золотой прямоугольник. Двенадцать вершин икосаэдра можно разбить на три взаимно перпендикулярных золотых прямоугольника, границы которых образуют кольца Борромео^[2].

Согласно популяризатору астрофизики и математики Марио Ливио, после публикации книги Пачоли О божественной пропорции в 1509 году^[3], когда золотая пропорция стала известна художникам без излишней математики^[4], многие художники и архитекторы были очарованы золотым сечением и оно принято ими как эстетически приятное. Пропорции золотого прямоугольника были известны и до публикации Пачоли^[5]: такие архитектурные шедевры, как Парфенон в Афинах или Альгамбра в Гранаде явно использовали пропорции золотого прямоугольника.

• Вилла Штейн^[en] (1927) архитектора Ле Корбюзье в Гарше в горизонтальном плане, в профиле и во внутренних структурах использует близкие к золотому прямоугольнику пропорции ^[6].
• Флаг Того разработан с пропорциями, близкими к золотому прямоугольнику^[7].

1. ↑ Euclid, Book XIII, Proposition 10.
2. ↑ Burger, Starbird, 2005, с. 382.
3. ↑ Pacioli, Luca. De divina proportione, Luca Paganinem de Paganinus de Brescia (Antonio Capella) 1509, Venice.
4. ↑ Livio, 2002.
5. ↑ Van Mersbergen, 1998.
6. ↑ Padovan, 1999, с. 320.
7. ↑ Flag of Togo (неопр.). FOTW.us. Flags Of The World. Дата обращения 9 июня 2007. Архивировано 7 июня 2007 года.

• Edward B. Burger, Michael P. Starbird. The Heart of Mathematics: An Invitation to Effective Thinking. — Springer, 2005. — ISBN 9781931914413.
• Mario Livio. The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number. — New York: Broadway Books, 2002. — ISBN 0-7679-0815-5.
• Audrey M. Van Mersbergen. Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic // Communication Quarterly. — 1998. — Т. 46. ‘Golden Rectangle’ has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.
• Le Corbusier. The Modulor. — С. 35., как цитировано у Падована Richard Padovan. Proportion: Science, Philosophy, Architecture. — Taylor & Francis, 1999. — С. 320. — ISBN 0-419-22780-6.: «Both the paintings and the architectural designs make use of the golden section».

Поперечное сечение прямоугольника формула

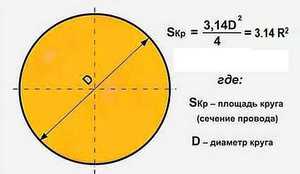В инженерной и строительной практике нередко встречаются задачи по расчёту площади поперечного сечения. Если фигуру разрезать по линии, которая перпендикулярна продольной оси предмета, то полученный торец и будет поперечным сечением. Круг — один из наиболее часто встречающихся видов подобного рассечения. Такой срез присущ цилиндру, шару, конусу, тору, эллипсоиду.

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

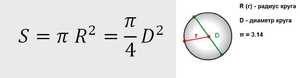
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

Область применения

Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:

1. Определение объемов емкостей.
2. Решение задач по сопротивлению материалов и электротехнике.
3. Расчет количества материалов при проектировании, строительстве и ремонте.
4. Ведение поливного земледелия.

Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.

Круг имеет ряд характеристик:

• радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
• диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
• длина окружности (C/c/L/l).

Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).

Способы расчета

Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.

Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.

При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.

Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).

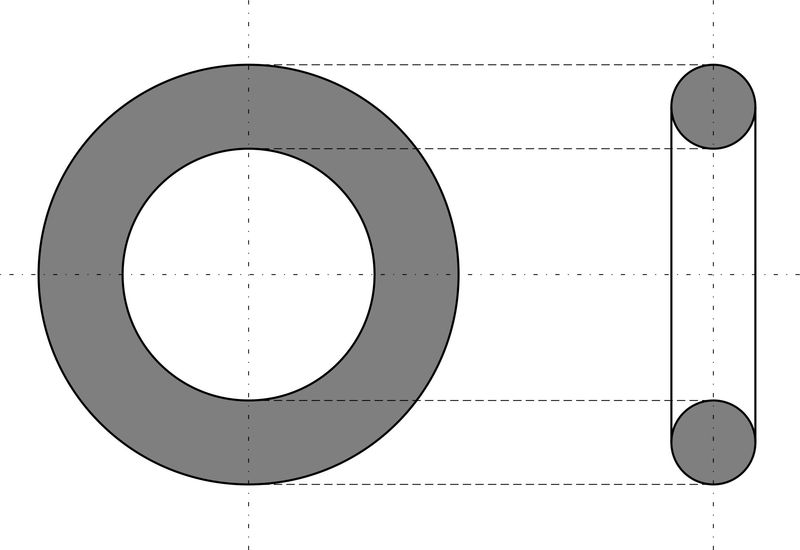
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:

1. Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
2. Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
3. Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.

Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».

Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые).

Сечение прямоугольника — это изображение фигуры, образованной рассечением прямоугольника плоскостью в поперечном или продольном направлении.

Формула для расчета площади поперечного сечения прямоугольника:

a — длина прямоугольника;
b — ширина прямоугольника.

Смотрите также статью о всех геометрических фигурах (линейных 1D, плоских 2D и объемных 3D).

Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета площади сечения прямоугольника, если известны его стороны. С помощью этого калькулятора вы в один клик сможете рассчитать поперечную площадь сечения прямоугольника если известна его сторона и высота.

Для заданной стальной балки подобрать размеры прямоугольного поперечного сечения по условию прочности.

Соотношение сторон сечения h=2b (h – высота, b – ширина).

Полученные размеры принять согласно ГОСТ 6636.
Допустимые напряжения для материала балки [ σ ]=160МПа.

Предыдущие пункты решения задачи:

Минимально необходимый расчетный момент сопротивления сечения балки составил

В случаях, когда система изгибающих нагрузок действующих на балку расположена в вертикальной плоскости сечение тоже следует располагать вертикально.

По справочнику находим формулу осевого момента сопротивления прямоугольного сечения

Используя заданное соотношение сторон (h=2b), уменьшим количество переменных в выражении

и запишем необходимое неравенство

откуда находим расчетную высоту прямоугольного сечения

Из заданного соотношения сторон определяем расчетную ширину сечения

Отметим, что полученные размеры являются минимально необходимыми для обеспечения прочности заданной балки.

При отсутствии дополнительных условий расчетные размеры можно округлить до целого значения в миллиметрах исключительно в большую сторону (h=153мм, b=77мм).

По ГОСТ 6636 нормальных линейных размеров выбираются ближайшие значения в сторону увеличения.

Следовательно, за окончательные размеры прямоугольного сечения балки принимаем: h=155мм, b=80мм.

После принятия размеров согласно ГОСТ заданное соотношение сторон может несколько измениться. Это нормально.

Расчет характеристик полого прямоугольного сечения

• ГЛАВНАЯ
  • расчеты
  • мониторинг
  • консалтинг
• ОБЪЕКТЫ
  • сосуды и аппараты
  • здания и сооружения
  • трубопроводы
  • прочие
• ОНЛАЙН
  • сосуды и аппараты
  • трубопроводы
  • прочие
  • математика
• МАТЕРИАЛЫ
  • статьи
  • презентации
  • отчеты
  • log-files
  • прочие
• ЛИТЕРАТУРА
  • сосуды и аппараты
  • здания и сооружения
  • трубопроводы
  • прочие
• Карта сайта

Искать…