1.Что изучает наука – электротехника? Электрическая цепь. Электрический ток

Электротехника — область технических наук, изучающая получение, распределение, преобразование и использование электрической энергии

Электрическая цепь  — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение

Цепи бывают:

Неразветвленные и разветвленные электрические цепи

Линейные и нелинейные электрические цепи

Неразветвленные— это когда во всех элементах ее течет один и тот же ток

Разветвленные— в каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей.

Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным относятся те компоненты, которые описываются линейным дифференциальным уравнением

Нелинейные- если цепь содержит отличные от перечисленных компоненты

Законы действующие в электрических цепях:

-Закон Ома

-Теорема Тевенина

-Правило токов Кирхгофа

-Правило напряжений Кирхгофа

Электрический ток — упорядоченное некомпенсированное движение свободных электрически заряженных частиц под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях — электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость)

Различают: Постоянный ток — ток, направление и величина которого слабо меняются во времени

Переменный ток — это ток, величина и (или) направление которого меняются во времени. Среди переменных токов основным является ток, величина которого изменяется по синусоидальному закону

2.Электрические цепи и ее элементы.

Электрическая цепь представляет собой совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении. В электрической цепи постоянного тока могут действовать как постоянные токи, так и токи, направление которых остается постоянным, а значение изменяется произвольно во времени или по какому-либо закону.

Электрическая цепь состоит из отдельных устройств или элементов, которые по их назначению можно разделить на 3 группы:

Первую группу составляют элементы, предназначенные для выработки электроэнергии (источники питания)

 Вторая группа — элементы, преобразующие электроэнергию в другие виды энергии (механическую, тепловую, световую, химическую и т. д.). Эти элементы называются приемниками электрической энергии (электроприемниками)

В третью группу входят элементы, предназначенные для передачи электроэнергии от источника питания к электроприемнику (провода, устройства, обеспечивающие уровень и качество напряжения, и др.).

Теория электрических цепей — Википедия

Материал из Википедии — свободной энциклопедии

Теория электрических цепей — совокупность наиболее общих закономерностей, описывающих процессы в электрических цепях. Теория электрических цепей основана на двух постулатах:

1. Исходное предположение теории электрических цепей. Все процессы в любых электротехнических устройствах можно описать с помощью двух понятий: тока и напряжения.
2. Исходное допущение теории электрических цепей. Сила тока в любой точке сечения любого проводника одна и та же, а напряжение между любыми двумя точками пространства изменяется по линейному закону^{[источник не указан 1145 дней]}.

Ток — количество зарядов (q, в Кулонах), перемещаемых через поперечное сечение проводника в единицу времени (t, в секундах).

i(t) = dq/dt или I = q/t , измеряется в Амперах = А

Напряжение — предел отношения количества энергии, необходимой для переноса некоторого количества электричества из одной точки пространства в другую, к этому количеству электричества, когда оно стремится к нулю. Последнее равенство написано в предположении, что энергия и заряд — величины непрерывные. Размерность напряжения:

В = Дж • Кл⁻¹

Из основных понятий как следствие вытекают определения:

Энергия — мера способности объекта совершать работу. Её размерность:

Дж = В • А • с

Мощность — скорость изменения энергии во времени. Размерность мощности:

Вт = Дж • с⁻¹ = В • А

Электрическая цепь[править | править код]

Электрическая цепь — совокупность элементов и источников, предназначенных для генерации, приема и преобразования токов и напряжений (электрических сигналов). Те участки цепи, куда поступают или для которых генерируются сигналы, называют входами; те участки, на которых регистрируют токи или напряжения в результате их генерации или преобразования, — выходами.

Элементы электрической цепи — идеализированные устройства с двумя или более зажимами, все электромагнитные процессы в которых с достаточной для практики точностью могут быть описаны только в основных понятиях (тока и напряжения).

Элементы бывают: линейные и нелинейные, пассивные и активные, стационарные и нестационарные, непрерывные и дискретные, с сосредоточенными и распределенными параметрами. Из дальнейшего рассмотрения исключим нестационарные элементы и элементы с распределенными параметрами. Источники электромагнитной энергии — идеализированные устройства, имеющие два или более зажимов и предназначенные для генерации или преобразования электромагнитной энергии. Источники бывают: независимые, зависимые и управляемые.

Ветвь[править | править код]

Ветвью называется участок электрической цепи с одним и тем же током. Ветвь состоит из одного активного или пассивного элемента или представляет собой последовательное соединение нескольких элементов.

Узел[править | править код]

Узлом называется место соединения трех и более ветвей. Различают понятия геометрического и потенциального узлов. Геометрические узлы, имеющие одинаковые потенциалы, могут быть объединены в один потенциальный узел.

Контур[править | править код]

Контуром называется замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи.

Двухполюсник[править | править код]

Двухполюсником называют часть электрической цепи с двумя выделенными зажимами-полюсами.

Четырёхполюсник[править | править код]

Четырёхполюсником называют часть электрической цепи, имеющую две пары зажимов, которые называются входными и выходными.

• Добротворский И. Н. Теория электрических цепей. Учебник. — М.: Радио и связь, 1989.
• В. Г. Герасимов, Э. В. Кузнецов, О. В. Николаева. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Вопрос №4. Понятие электрической цепи постоянного тока. Электродвижущая сила (20 мин.)

Одна из важнейших задач электротехники – передача электрической энергии на дальние и ближние расстояния. Этот процесс осуществляется по электрическим цепям.

Электрическая цепь – совокупность устройств, предназначенных для получения, передачи, преобразования и использования электри­ческой энергии.

Электрическая цепь состоит из источников электрической энергии, передающих и преобразующих элементов, приемников электроэнергии.

Источники электрической энергии осуществляют преобразо­вание в электрическую энергию каких-либо других видов энергии – механической (генераторах электрической энергии), тепловой (термопреобразователи), химической (аккумуляторы, гальванические элементы), световой (фотогенераторы) и др.

Приемники электрической энергии или потребители пре­образуют электроэнергию в другие виды энергии, например, в механическую (электродвигатели), тепловую (электрические печи, нагревательные приборы), химическую (электролизные ванны), световую (лампы накаливания).

Передающие элементы цепи служат для передачи электрической энергии от источников, рас­пределения ее между приемниками и контроля режима работы всех электротехнических устройств. К ним относятся коммутационная аппаратура (аппараты для включения и от­ключения цепи, предохранители), преобразующие устройства (трансформаторы), линии и измерительные приборы.

Классификация электрических цепей приведена в таблице 4.

Таблица 4

Классификация электрических цепей
По виду тока
Цепи постоянного тока		Цепи переменного тока
По содержанию элементов
Линейные цепи (содержат только линейные элементы)		Нелинейные цепи (содержат хотя бы один нелинейный элемент)
По конфигурации
Простые (содержат один источник питания и один контур)	Сложные (содержат два и более источников питания и контуров)	Неразветвленные (содержат один контур)	Разветвленные (содержат много контуров)

Основной задачей изучения электротехники является овладение методиками расчетов электрических цепей. Для того, чтобы произвести расчет реальной электрической цепи необходимо составить ее схемы (табл. 5).

Таблица 5

Электрическая схема
Эскизная	Принципиальная	Схема замещения
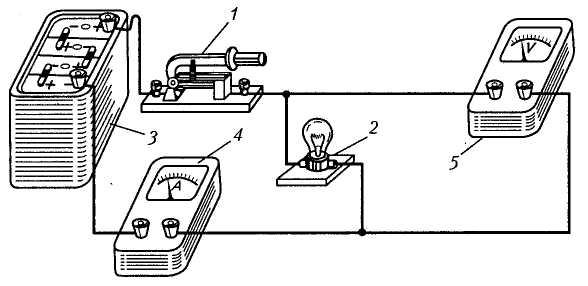
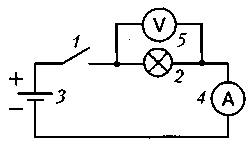
Реальное изображение электротехнических устройств и способов их соединения 1 – рубильник, 2 – лампа накаливания (приемник электрической энергии), 3 – аккумуляторная батарея (источник элек­трической энергии постоянного тока), контролирующие приборы – амперметр (4) и вольтметр (5)	Графическое изображение цепи, в которой каждое электротехническое устройство заменено (согласно ГОСТам) его условным обозначением	Графическое отображение электрической цепи с использованием различных идеализированных элементов (источников питания, резисторов, конденсаторов, катушек индуктивности и т.д.), выбранных так, чтобы можно было с заданным или необходимым приближением описать процессы в цепи

Для того, чтобы выполнить расчет электрической цепи необходимо составить ее схему замещения. Элементами электрической цепи являются источники электрической энергии, активные и реактивные сопротивления.

Условные графические обозначения некоторых элементов электрической цепи приведены в табл. 6.

Таблица 6

Элемент электрической цепи	Условное обозначение	Элемент электрической цепи	Условное обозначение
Термопара		Лампа накаливания сигнальная
Фотоэлемент		Катушка индуктивности
Гальванический элемент (ГЭ) или аккумулятор		Катушка индуктивности с ферромагнитным сердечником
Источник ЭДС		Источник тока
Батарея ГЭ или аккумуляторов		Конденсатор
Линия электрической связи		Конденсатор регулируемый
Узел цепи		Контакт выключателя
Заземление		Переключатель
Резистор		Штепсельный разъем
Реостат		Плавкий предохранитель
Реостат		Амперметр
Варистор (нелинейный резистор)		Вольтметр
Лампа накаливания осветительная		Ваттметр

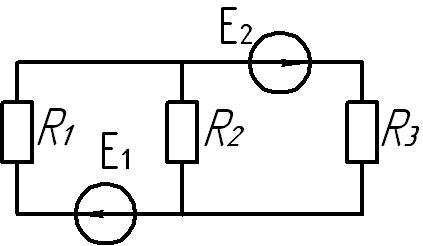
Для описания электрической цепи используются топологические понятия, основными из которых являются узел, ветвь и контур (рис. 17).

Ветвь – совокупность связанных элементов электрической цепи между двумя узлами. Это участок цепи, по которому протекает один и тот же ток. Ветвь по определению содержит элементы.

Узел – место соединения не менее трех ветвей.

Контур – замкнутый путь, про­ходящий по нескольким ветвям так, что ни одна ветвь и ни один узел не встречается больше одного раза.

Контур называется элементарным, если содержит хотя бы одну ветвь, не входящую в другие выбранные контуры, и неэлементарным, если все ветви данного контура входят в другие выбранные контуры (рис. 18).

По определению различные контуры электрической цепи должны отличаться друг от друга по крайней мере одной ветвью. Количество контуров, которые могут быть образованы для данной электрической цепи, ограничено и определено.

Рис. 18

Например, укажите максимальное число контуров, которые можно образовать в этой цепи (рис. 19) с участием R₁.

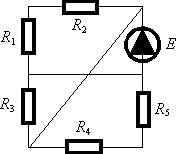
Рис. 19

Укажите максимальное число контуров, которые можно образовать в этой цепи (рис. 19).

Элементы электрической цепи подразделяются на: активные − источники электрической энергии и пассивные, т.е. не способные генерировать электрическую энергию (приемники электроэнергии).

Источник электрической энергии, включенный в замкнутую электрическую цепь, расходует энергию на преодоление сопротивления внешней и внутренней (внутреннего сопротивления самого источника) цепей (рис. 20). В сопротивлении происходит необратимый процесс преобразования электрической энергии в тепловую.

Рис. 20

Чтобы в электрической цепи протекал ток, необходимо иметь разность потенциалов на зажимах цепи. Эту разность потенциалов создают источники электродвижущей силы. В каждом источнике электрической энергии действуют сторонние силы.

Сторонние силы – это силы неэлектрического происхождения, вызывающие разделение зарядов.

Например, сторонними силами являются:

• в электрических генераторах – механическая сила, под действием которой проводник перемещается в магнитном поле, в результате чего в проводнике возникает электродвижущая сила;

• в химических источниках тока (гальванические элементы, аккумуляторы) – химическая реакция;

• в термогенераторах – нагрев места спая двух разнородных металлов;

• в фотоэлементах – действие светового потока на пластину цезия.

Сторонние силы перемещают внутри источников эклектической энергии электрические заряды, в результате чего энергия одного вида превращается в энергию другого вида. Если к источнику электрической энергии подключить приемники, то в цепи будет протекать электрический ток.

При существовании тока в электрической цепи источник совершает работу.

Электродвижущая сила источника (ЭДС) – работа, затрачиваемая сторонними силами на перемещение единицы положительного заряда от меньшего потенциала к большему. Единица измерения – Вольт.

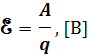
где E – электродвижущая сила; А — работа, Дж; q – величина электрического заряда, Кл.

Таким образом, условное обозначение источника ЭДС включает два элемента. Первый из них кружок со стрелкой указывает, что в источнике есть ЭДС Е, стрелка показывает направление ЭДС. При этом ток в источнике за счет действия сторонних (не электрических) сил протекает от отрицательного зажима к положительному, от зажима с меньшим потенциалом к зажиму с большим. Второй элемент с с сопротивлением r_вн или иногда его обозначают r₀ характеризует преобразование электроэнергии внутри источника в тепло, иными словами потери энергии внутри источника (рис. 21).

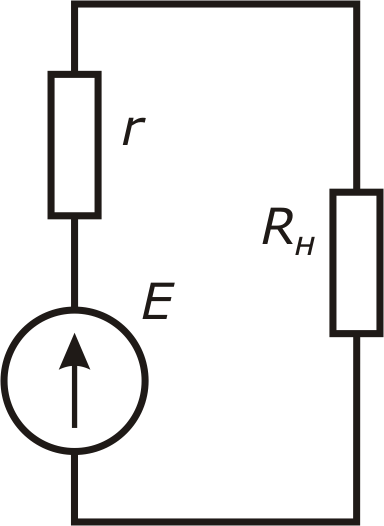
Рис. 21

Направление перемещения положительных зарядов, а следовательно, и направление тока, протекающего в замкнутой цепи, совпадает с направлением ЭДС. При протекании тока через участок, имеющий сопротивление, на концах этого участка возникают потенциалы φ₁ и φ₂, разность которых равна напряжению, падающему на этом участке U₁₂ (рис. 22).

На каждом участке цепи (рис. 20) ток протекает от точки с большим потенциалом (φ₁) к точке с меньшим потенциалом (φ₂).

Рис. 22

Источниками постоянного тока являются генераторы постоянного тока, аккумуляторы и гальванические элементы (рис. 23).

а)	б)	в)
Рис. 23. Виды источников постоянного тока: а) батарейка; б) генератор постоянного тока; в) аккумулятор

Постоянный ток применяется при электрохимическом получении алюминия, на городском и железнодорожном электротранспорте, в электронике, медицине и других областях на­уки и техники. В настоящее время быстрыми темпами развиваются и совершенствуются различные альтернативные источники электрической энергии постоянного тока – сол­нечные батареи, фотоэлементы, МГД-генераторы.

Электротехника — Википедия

Электроте́хника — область техники, связанная с получением, распределением, преобразованием и использованием электрической энергии. А также — c разработкой, эксплуатацией и оптимизацией электронных компонентов, электронных схем и устройств, оборудования и технических систем^[1]. Под электротехникой также понимают техническую науку, которая изучает применение электрических и магнитных явлений для практического использования^[2][3][4]. Электротехника выделилась в самостоятельную науку из физики в конце XIX века. В настоящее время электротехника как наука включает в себя следующие научные специальности: электромеханика, ТОЭ, светотехника, силовая электроника. Кроме того, к отраслям электротехники часто относят энергетику^[2], хотя легитимная классификация^[5] рассматривает энергетику как отдельную техническую науку. Основное отличие электротехники от слаботочной электроники заключается в том, что электротехника изучает проблемы, связанные с силовыми крупногабаритными электронными компонентами: линии электропередачи, электрические приводы, в то время как в электронике основными компонентами являются компьютеры и другие устройства на базе интегральных схем, а также сами интегральные схемы^[6]. В другом смысле, в электротехнике основной задачей является передача электрической энергии, а в слаботочной электронике — информации.

Основы для развития электротехники заложили обширные экспериментальные исследования и создание теорий электричества и магнетизма. Широкое практическое применение электричества стало возможно только в XIX веке с появлением вольтова столба, что позволило как найти приложение открытым законам, так и углубить исследования. В этот период вся электротехника базировалась на постоянном токе.

В конце XIX века, с преодолением проблемы передачи электроэнергии на большие расстояния за счёт использования переменного тока и созданием трёхфазного электродвигателя, электричество повсеместно внедряется в промышленность, а электротехника приобретает современный вид, включающий множество разделов, и оказывает влияние на смежные отрасли науки и техники^[4].

Электричество является своеобразной «разменной монетой» в области преобразования и использования энергии. Электричество возможно получить множеством различных способов: механическим (мускульные, гидро- ,ветро-, паро-, ДВС-генераторы и т.д, трибоэлектризация, пьезоэлектричество, эффект Виллари, опыт Мандельштама-Папалекси), тепловым (термопары, РИТЭГи), химическим (гальванические батареи, аккумуляторы, топливные элементы, МГД-генераторы), световым (фотогальванические элементы, наноантенны), биологическим (электрический скат, электрический угорь), звуковым (микрофоны), индукционным (антенны, ректенны). В то же время можно реализовывать обратные процессы — преобразование электричества в механическое усилие (электродвигатели, электромагниты, магнитострикция, МГД-насосы, опыты Гальвани, электромиостимуляция), тепло (ТЭНы, индукционный нагрев, искровой поджиг, элементы Пельтье), световое, УФ- и ИК-излучение (лампы накаливания, светодиоды), химические процессы (электрохимия, плазмогенераторы, гальваностегия, гальванопластика), звуковые волны (динамические головки, пьезоизлучатели), элекромагнитное излучение (антенны, магнетроны, лампы бегущей волны). Этими же методами возможно фиксировать различные параметры промышленных, бытовых и научных приборов. Таким образом, используя одно физическое явление, можно удовлетворить огромное множество потребностей человека. Именно это обеспечило широчайшее применение электричества в современном быту, промышленности и научных исследованиях.

Электротехника имеет множество разделов, самые важные из которых описаны ниже. Хотя инженеры работают каждый в своей области, многие из них имеют дело с комбинацией из нескольких наук.

Электроэнергетика[править | править код]

Электроэнергетика — наука о выработке, передаче и потреблении электроэнергии, а также о разработке устройств для этих целей. К таким устройствам относят: трансформаторы, электрические генераторы, ТЭНы, электродвигатели, низковольтную аппаратуру и электронику для управления силовыми приводами. Многие государства мира имеют электрическую сеть, называемую электроэнергетической системой, которая соединяет множество генераторов с потребителями энергии. Потребители получают энергию из сети, не тратя ресурсы на выработку своей собственной энергии. Энергетики работают как над проектированием и обслуживанием сети, так и над энергетическими системами, присоединёнными к сети. Такие системы называются внутрисетевыми и могут как поставлять энергию в сеть, так и потреблять её. Энергетики работают также и над системами, не присоединёнными к сети, называемыми внесетевыми, которые в некоторых случаях являются более предпочтительными, чем внутрисетевые системы. Имеется перспектива создания энергетических систем, контролируемых со спутника, имеющих обратную связь в реальном времени, что позволит избежать скачков напряжения и предотвратить нарушения энергоснабжения.

Электромеханика[править | править код]

Электромеханика  рассматривает общие принципы электромеханического преобразования электрической энергии и их практическое применение для проектирования и эксплуатации электрических машин. Предметами изучения электромеханики являются: преобразование электрической энергии в механическую и наоборот, электрические машины, электромеханические комплексы и системы. Цель электромеханики — управление режимами работы и регулирование параметров обратимого преобразования электрической энергии в механическую. К основным направлениям электромеханики относятся: общая теория электромеханического преобразования энергии; проектирование электрических машин;анализ переходных процессов в электрических машинах.

Системы автоматического управления[править | править код]

Задачами автоматических систем управления (и автоматизации в целом) является моделирование различных динамических систем и разработка систем управления, которые заставляют работать динамические системы нужным образом. Для создания таких устройств могут использоваться электрические схемы, процессоры цифровой обработки сигналов, микроконтроллеры и программируемые логические контроллеры. Системы управления имеют широкую область применения от систем, встраиваемых в энергетические установки (например, на коммерческих авиалайнерах), автоматов постоянной скорости (имеющихся во множестве современных автомобилей) и ЧПУ в станках до систем управления на базе промышленных ПК в автоматизации промышленного производства.

Инженеры часто используют обратную связь при проектировании систем управления. Например, в автомобиле с автоматом постоянной скорости скорость транспортного средства постоянно отслеживается, и данные передаются системе, которая соответственно регулирует выходную мощность двигателя. Если имеется стандартная система обратной связи, можно использовать теорию управления для определения того, как система должна реагировать на поступающую информацию.

Электроника[править | править код]

Метод контурных токов — Википедия

Ме́тод ко́нтурных то́ков — метод сокращения размерности системы уравнений, описывающей электрическую цепь.
Метод контурных токов — метод расчёта электрических цепей, при котором за неизвестные принимаются токи в контурах, образованных некоторым условным делением электрической цепи.

Любая электрическая цепь, состоящая из Р рёбер (ветвей, участков, звеньев) и У узлов, может быть описана системой уравнений в соответствии с 1-м и 2-м правилами Кирхгофа. Число уравнений в такой системе равно Р, из них У–1 уравнений составляется по 1-му правилу Кирхгофа для всех узлов, кроме одного; а остальные Р–У+1 уравнений – по 2-му правилу Кирхгофа для всех независимых контуров. Поскольку независимыми переменными в цепи считаются токи рёбер, число независимых переменных равно числу уравнений, и система разрешима.

Существует несколько методов сократить число уравнений в системе. Одним из таких методов является метод контурных токов.

Метод использует тот факт, что не все токи в рёбрах цепи являются независимыми. Наличие в системе У–1 уравнений для узлов означает, что зависимы У–1 токов. Если выделить в цепи Р–У+1 независимых токов, то систему можно сократить до Р–У+1 уравнений. Метод контурных токов основан на очень простом и удобном способе выделения в цепи Р–У+1 независимых токов.

Метод контурных токов основан на допущении, что в каждом из Р–У+1 независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторое ребро принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ребро принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любое ребро принадлежит хотя бы одному контуру), то ток в любом ребре можно выразить через контурные токи, и контурные токи составляют полную систему токов.

Использование планарных графов[править | править код]

Наиболее простым и наглядным методом построения системы независимых контуров является построение планарного графа схемы, то есть размещение ветвей и узлов цепи на плоскости без взаимных пересечений рёбер. Планарный граф разбивает плоскость на К ограниченных областей. Можно показать, что замкнутые цепочки рёбер, ограничивающие эти области, являются системой независимых контуров для рассматриваемой схемы.

Метод планарного графа предпочтителен при ручном расчёте схем. В случае, если схему невозможно изобразить в виде планарного графа, а также в случае компьютерного построения системы контуров применение этого метода может оказаться невозможным.

Метод выделения максимального дерева[править | править код]

Дерево представляет собой подмножество звеньев цепи, представляющее собой односвязный (то есть состоящий из одной части) граф, в котором нет замкнутых контуров. Дерево получается из цепи путём исключения из него некоторых звеньев. Максимальное дерево — это дерево, для которого добавление к нему любого исключённого звена приводит к образованию контура.

Метод выделения максимального дерева основан на последовательном исключении из цепи определённых звеньев согласно следующим правилам:

• На каждом шагу из цепи в произвольном порядке исключается одно звено;
• Если исключение звена приводит к нарушению односвязности графа (то есть граф разбивается на две изолированных части, либо появляются «висящие» узлы), то звено возвращается в цепь;
• Если при исключении звена граф не теряет односвязности, звено остаётся исключённым;
• Переходим к следующему шагу.

В конце работы алгоритма число исключённых из цепи звеньев оказывается точно равно числу независимых контуров схемы. Каждый независимый контур получается присоединением к цепи соответствующего исключённого звена.

Пример выделения максимального дерева

• Удаление звена R1

• Удаление звеньев R2 и R3

• Удаление звена R4 приводит к появлению «висячего» узла

• Присоединение к дереву удалённого звена образует контур

Для построения системы уравнений необходимо выделить в цепи P – У + 1 независимых контуров. По каждому из этих контуров будет составлено одно уравнение по 2-му закону Кирхгофа. В каждом контуре необходимо выбрать направление обхода (например, по часовой стрелке).

Выделение независимых контуров можно осуществить одним из перечисленных выше методов. Следует отметить, что система независимых контуров, как правило, не единственна, как не единственно и максимальное дерево цепи. Однако системы уравнений, составленные по различным системам контуров, математически эквивалентны, поэтому возможен специальный подбор системы контуров, дающей наиболее простую систему уравнений.

Отметим также, что при любом выборе системы контуров в любом контуре обязательно найдётся ребро, которое входит только в этот контур и ни в какой другой. Таким образом, контурный ток всегда совпадает с током в одном из рёбер этого контура. Например, для схемы, изображённой на рисунке, звено 4 входит только в левый контур, поэтому контурный ток обозначен как I₄. То же самое относится к двум другим контурам, токи в которых обозначены как I₅ и I₆. В литературе встречаются и другие обозначения для контурных токов, например, римскими цифрами (I_I, I_II, I_III …), латинскими буквами (I_A, I_B, I_C …) и т.д.

Принцип построения системы уравнений следующий.

• Все токи в звеньях выражаем через контурные токи. В данном случае необходимо выразить только те токи, которые не совпадают с одним из контурных токов:

I1=I6−I4;I2=I5−I4;I3=I6−I5;{\displaystyle I_{1}=I_{6}-I_{4};\quad I_{2}=I_{5}-I_{4};\quad I_{3}=I_{6}-I_{5};}

• Для каждого контура записываем уравнение по второму закону Кирхгофа:
  • В левой части каждого уравнения записываем сумму токов в звеньях, входящих в контур, умноженных на сопротивление соответствующего звена. Суммирование происходит с учётом знака: если ток в звене совпадает с направлением обхода контура, слагаемое записывается со знаком «плюс», в противном случае — со знаком «минус».
  • В правой части каждого уравнения записываем сумму ЭДС источников, а также сумму произведений токов источников на сопротивление соответствующего звена. Суммирование также происходит с учётом знака, в зависимости от совпадения или несовпадения направления источника с направлением контурного тока:

Рис. 1. Пример электрической схемы

Для первого контура (I₄):

−I1Z1−I2Z2+I4Z4=E4;{\displaystyle -I_{1}Z_{1}-I_{2}Z_{2}+I_{4}Z_{4}=E_{4};}

−(I6−I4)Z1−(I5−I4)Z2+I4Z4=E4;{\displaystyle -(I_{6}-I_{4})Z_{1}-(I_{5}-I_{4})Z_{2}+I_{4}Z_{4}=E_{4};}

(Z1+Z2+Z4)I4−Z2I5−Z1I6=E4;{\displaystyle (Z_{1}+Z_{2}+Z_{4})I_{4}-Z_{2}I_{5}-Z_{1}I_{6}=E_{4};}

Для второго контура (I₅):

I2Z2−I3Z3+I5Z5=J5Z5;{\displaystyle I_{2}Z_{2}-I_{3}Z_{3}+I_{5}Z_{5}=J_{5}Z_{5};}

(I5−I4)Z2−(I6−I5)Z3+I5Z5=J5Z5;{\displaystyle (I_{5}-I_{4})Z_{2}-(I_{6}-I_{5})Z_{3}+I_{5}Z_{5}=J_{5}Z_{5};}

−Z2I4+(Z2+Z3+Z5)I5−Z3I6=J5Z5;{\displaystyle -Z_{2}I_{4}+(Z_{2}+Z_{3}+Z_{5})I_{5}-Z_{3}I_{6}=J_{5}Z_{5};}

Для третьего контура (I₆):

I1Z1+I3Z3+I6Z6=E6;{\displaystyle I_{1}Z_{1}+I_{3}Z_{3}+I_{6}Z_{6}=E_{6};}

(I6−I4)Z1+(I6−I5)Z3+I6Z6=E6;{\displaystyle (I_{6}-I_{4})Z_{1}+(I_{6}-I_{5})Z_{3}+I_{6}Z_{6}=E_{6};}

−Z1I4+−Z3I5+(Z1+Z3+Z6)I6=E6;{\displaystyle -Z_{1}I_{4}+-Z_{3}I_{5}+(Z_{1}+Z_{3}+Z_{6})I_{6}=E_{6};}

Окончательно получаем систему уравнений

{(Z1+Z2+Z4)⋅I4−Z2⋅I5−Z1⋅I6=E4−Z2⋅I4+(Z2+Z3+Z5)⋅I5−Z3⋅I6=Z5J5−Z1⋅I4−Z3⋅I5+(Z1+Z3+Z6)⋅I6=E6.{\displaystyle {\begin{cases}(Z_{1}+Z_{2}+Z_{4})\cdot I_{4}-Z_{2}\cdot I_{5}-Z_{1}\cdot I_{6}=E_{4}\\-Z_{2}\cdot I_{4}+(Z_{2}+Z_{3}+Z_{5})\cdot I_{5}-Z_{3}\cdot I_{6}=Z_{5}J_{5}\\-Z_{1}\cdot I_{4}-Z_{3}\cdot I_{5}+(Z_{1}+Z_{3}+Z_{6})\cdot I_{6}=E_{6}\end{cases}}.}

Оптимизированная процедура составления системы[править | править код]

Как видно из вышесказанного, процедуру составления системы можно упростить следующим образом:

• В левой части К-го уравнения записываем произведение контурного тока на сумму сопротивлений всех звеньев, входящих в контур:

IK(ZK1+ZK2+…)+…,{\displaystyle I_{K}(Z_{K1}+Z_{K2}+…)+…,}

где  IK{\displaystyle \ I_{K}} — ток контура, для которого записывается уравнение;

 ZK1…ZKn{\displaystyle \ Z_{K1}…Z_{Kn}} — сопротивления звеньев, входящих в этот контур.

• От левой части уравнения отнимаем остальные контурные токи, умноженные на суммы сопротивлений звеньев, по которым контур К пересекается с этими контурами:

…−IA(ZKA1+ZKA2+…)−IB(ZKB1+ZKB2+…)−…{\displaystyle …-I_{A}(Z_{KA1}+Z_{KA2}+…)-I_{B}(Z_{KB1}+Z_{KB2}+…)-…}

где  IA,IB,…{\displaystyle \ I_{A},I_{B},…} — токи контуров, пересекающихся с контуром К;

 ZKA1,ZKA2,…{\displaystyle \ Z_{KA1},Z_{KA2},…} — сопротивления звеньев, входящих одновременно в контура К и A.

• В правой части уравнения записываем сумму источников ЭДС с учётом знаков («плюс» — если направления ЭДС и обхода контура совпадают, «минус» — в противном случае):

…=±EK1±EK2…{\displaystyle …=\pm E_{K1}\pm E_{K2}…}

• К правой части уравнения прибавляем величины источников тока, умноженные на сопротивление соответствующего звена с учётом знаков («плюс» — если направления источника тока и обхода контура совпадают, «минус» — в противном случае):

…±JK1ZK1±JK2ZK2…{\displaystyle …\pm J_{K1}Z_{K1}\pm J_{K2}Z_{K2}…}

Составив уравнения для всех независимых контуров, получаем совместную систему P–У+1 уравнений относительно P–У+1 неизвестных контурных токов.

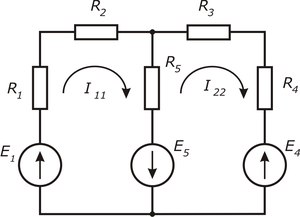Рис. 2. Метод контурных токов

Положим, что в левом контуре по часовой стрелке течет контурный ток I₁₁, а в правом (также по часовой стрелке) — контурный ток I₂₂. Для каждого из контуров составим уравнения по второму закону Кирхгофа. При этом учтем, что по смежной ветви (с сопротивлением R₅) течет сверху вниз ток I₁₁–I₂₂. Направления обхода контуров примем также по часовой стрелке.

{(R1+R2+R5)I11+(−R5)I22=E1+E5(−R5)I11+(R3+R4+R5)I22=−E5−E4{\displaystyle {\begin{cases}(R_{1}+R_{2}+R_{5})I_{11}+(-R_{5})I_{22}=E_{1}+E_{5}\\(-R_{5})I_{11}+(R_{3}+R_{4}+R_{5})I_{22}=-E_{5}-E_{4}\\\end{cases}}}

Перепишем эти уравнения следующим образом:

{R11I11+R12I22=E11R21I11+R22I22=E22,{\displaystyle {\begin{cases}R_{11}I_{11}+R_{12}I_{22}=E_{11}\\R_{21}I_{11}+R_{22}I_{22}=E_{22}\\\end{cases}},}

где

R11=R1+R2+R5{\displaystyle R_{11}=R_{1}+R_{2}+R_{5}} — полное сопротивление первого контура;

R22=R3+R4+R5{\displaystyle R_{22}=R_{3}+R_{4}+R_{5}} — полное сопротивление второго контура;

R12=R21=−R5{\displaystyle R_{12}=R_{21}=-R_{5}} — сопротивления смежной ветви между первым и вторым контурами, взятые со знаком минус;

E11=E1+E5{\displaystyle E_{11}=E_{1}+E_{5}} — контурная ЭДС первого контура;

E22=−E4−E5{\displaystyle E_{22}=-E_{4}-E_{5}} — контурная ЭДС второго контура.

В матричном виде система уравнений для метода контурных токов выглядит следующим образом^[1]:

CZCtI2=C(E+ZJ),{\displaystyle \mathbf {CZC^{t}I_{2}=C(E+ZJ)} ,}

где

C{\displaystyle \mathbf {C} } — матрица контуров размера n × p (где n — количество независимых контуров, р — количество звеньев) , в которой i–я строка соответствует независимому контуру i, а j–й столбец соответствует звену j, причём элемент C_ij равен

• 0, если ребро j не входит в контур i;
• 1, если ребро входит в контур, и направление ребра соответствует направлению обхода контура;
• –1, если ребро входит в контур, и направление ребра противоположно направлению обхода контура.

Для каждого ребра задаётся направление, которое обычно ассоциируется с направлением тока в этом ребре;

Z{\displaystyle \mathbf {Z} } — диагональная матрица сопротивлений размера p × p, в которой диагональный элемент Z_ii равен сопротивлению i–го ребра, а недиагональные элементы равны нулю;

Ct{\displaystyle \mathbf {C} ^{t}} — транспонированная матрица контуров;

I2{\displaystyle \mathbf {I} _{2}} — матрица-столбец контурных токов размером n × 1.

J{\displaystyle \mathbf {J} } — матрица-столбец источников тока размером p × 1, где каждый элемент равен току источника в соответствующем ребре, причём эта величина нулевая, если в данном ребре источник тока отсутствует; положительная, если направление тока источника совпадает с направлением тока в ребре; и отрицательная в противном случае;

E{\displaystyle \mathbf {E} } — матрица-столбец источников ЭДС размером p × 1, где каждый элемент равен ЭДС источника в соответствующем ребре, причём эта величина нулевая, если в данном ребре источник ЭДС отсутствует; положительная, если направление ЭДС источника совпадает с направлением тока в ребре; и отрицательная в противном случае.

Пример системы уравнений[править | править код]

Для схемы, представленной в предыдущем разделе (см. «Построение системы уравнений», рис. 1), матрицы имеют вид:

C=(−1−1010001−1010101001);I2=(I4I5I6){\displaystyle \mathbf {C} ={\begin{pmatrix}-1&-1&0&1&0&0\\0&1&-1&0&1&0\\1&0&1&0&0&1\end{pmatrix}};\quad \mathbf {I} _{2}={\begin{pmatrix}I_{4}\\I_{5}\\I_{6}\end{pmatrix}}}

Ct=(−101−1100−11100010001);Z=(Z1000000Z2000000Z3000000Z4000000Z5000000Z6);J=(0000J50);E=(000E40E6){\displaystyle \mathbf {C} ^{t}={\begin{pmatrix}-1&0&1\\-1&1&0\\0&-1&1\\1&0&0\\0&1&0\\0&0&1\\\end{pmatrix}};\quad \mathbf {Z} ={\begin{pmatrix}Z_{1}&0&0&0&0&0\\0&Z_{2}&0&0&0&0\\0&0&Z_{3}&0&0&0\\0&0&0&Z_{4}&0&0\\0&0&0&0&Z_{5}&0\\0&0&0&0&0&Z_{6}\\\end{pmatrix}};\quad \mathbf {J} ={\begin{pmatrix}0\\0\\0\\0\\J_{5}\\0\end{pmatrix}};\quad \mathbf {E} ={\begin{pmatrix}0\\0\\0\\E_{4}\\0\\E_{6}\end{pmatrix}}}

Перемножаем матрицы в соответствии с матричным уравнением:

CZ=(−Z1−Z20Z4000Z2−Z30Z50Z10Z300Z6);{\displaystyle \mathbf {CZ} ={\begin{pmatrix}-Z_{1}&-Z_{2}&0&Z_{4}&0&0\\0&Z_{2}&-Z_{3}&0&Z_{5}&0\\Z_{1}&0&Z_{3}&0&0&Z_{6}\end{pmatrix}};}

CZCt=(Z1+Z2+Z4−Z2−Z1−Z2Z2+Z3+Z5−Z3−Z1−Z3Z1+Z3+Z6);{\displaystyle \mathbf {CZC^{t}} ={\begin{pmatrix}Z_{1}+Z_{2}+Z_{4}&-Z_{2}&-Z_{1}\\-Z_{2}&Z_{2}+Z_{3}+Z_{5}&-Z_{3}\\-Z_{1}&-Z_{3}&Z_{1}+Z_{3}+Z_{6}\end{pmatrix}};}

CZCtI2=((Z1+Z2+Z4)⋅I4−Z2⋅I5−Z1⋅I6−Z2⋅I4+(Z2+Z3+Z5)⋅I5−Z3⋅I6−Z1⋅I4−Z3⋅I5+(Z1+Z3+Z6)⋅I6);{\displaystyle \mathbf {CZC^{t}I_{2}} ={\begin{pmatrix}(Z_{1}+Z_{2}+Z_{4})\cdot I_{4}-Z_{2}\cdot I_{5}-Z_{1}\cdot I_{6}\\-Z_{2}\cdot I_{4}+(Z_{2}+Z_{3}+Z_{5})\cdot I_{5}-Z_{3}\cdot I_{6}\\-Z_{1}\cdot I_{4}-Z_{3}\cdot I_{5}+(Z_{1}+Z_{3}+Z_{6})\cdot I_{6}\end{pmatrix}};}

E+ZJ=(000E4Z5J

Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в технической литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи.

Решения систем линейных уравнений, составленных на основе правил Кирхгофа, позволяют найти все токи и напряжения в электрических цепях постоянного, переменного и квазистационарного тока^[1].

Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей.

Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений и, соответственно, при решении этой системы найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Определения[править | править код]

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило[править | править код]

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑j=1nIj=0.{\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило[править | править код]

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑k=1nEk=∑k=1mUk=∑k=1mRkIk;{\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑k=1nek=∑k=1muk=∑k=1mRkik+∑k=1muLk+∑k=1muCk.{\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений[править | править код]

Если цепь содержит p{\displaystyle p} узлов, то она описывается p−1{\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m{\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве mi{\displaystyle m_{i}}, то она описывается m−mi−(p−1){\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p−1{\displaystyle p-1} узлов или m−(p−1){\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

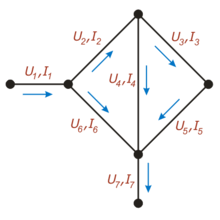На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p−1=2{\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m−mi−(p−1)=2{\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{I1−I2−I6=0I2−I4−I3=0{\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{U2+U4−U6=0U3+U5−U4=0{\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Первое правило Кирхгофа может быть сформулировано в матричном виде. Именно, пусть электрическая цепь состоит из n{\displaystyle n} узлов. Составим матрицу A={aij}i,j=1n{\displaystyle A=\{a_{ij}\}_{i,j=1}^{n}}, где aij{\displaystyle a_{ij}} при i≠j{\displaystyle i\neq j} есть проводимость ветви, соединяющеей узлы с номерами i{\displaystyle i} и j{\displaystyle j} (если они не соединены, можно мысленно соединить их ветвью нулевой проводимости). Величины aii{\displaystyle a_{ii}} положим равными ∑i=1, i≠jn(−aij){\displaystyle \sum _{i=1,~i\neq j}^{n}(-a_{ij})}. Пусть U{\displaystyle U} — потенциал, который мы рассматриваем как функцию, определённую на множестве узлов (или, что то же самое, вектор u=(U1,U2,…,Un){\displaystyle \mathbf {u} =(U_{1},U_{2},\dots ,U_{n})} в n{\displaystyle n}-мерном пространстве Rn{\displaystyle \mathbb {R} ^{n}}). Тогда по определению проводимости имеем Iij=aij(Uj−Ui){\displaystyle I_{ij}=a_{ij}(U_{j}-U_{i})}, где Iij{\displaystyle I_{ij}} — ток в ветви, идущей из вершины i{\displaystyle i} в вершину j{\displaystyle j}. Стало быть, первое правило Кирхгофа для j{\displaystyle j}-того узла можно записать как ∑i=1, i≠jnIij=∑i=1, i≠jnaij(Uj−Ui)=0{\displaystyle \sum _{i=1,~i\neq j}^{n}I_{ij}=\sum _{i=1,~i\neq j}^{n}a_{ij}(U_{j}-U_{i})=0}, или же ∑i=1, i≠jnaijUj+(∑i=1, i≠jn(−aij))Ui=0{\displaystyle \sum _{i=1,~i\neq j}^{n}a_{ij}U_{j}+\left(\sum _{i=1,~i\neq j}^{n}(-a_{ij})\right)U_{i}=0}, или же, учитывая определение диагональных элементов матрицы, как ∑i=1naijUj=0{\displaystyle \sum _{i=1}^{n}a_{ij}U_{j}=0}. В левой части равенства легко узнать координату произведения матрицы A{\displaystyle A} на вектор-столбец u{\displaystyle \mathbf {u} }. Итак, первое правило Кирхгофа в матричном виде гласит: Au=0{\displaystyle A\mathbf {u} =0}.

В таком виде оно допускает обобщение на проводящие поверхности. У криволинейной поверхности проводимость зависит не только от точки, но и от направления. Иными словами, проводимость является функцией на касательных векторах к поверхности. Если считать, что на касательных пространствах она хорошо приближается положительно определённой квадратичной формой, можно говорить о ней как о римановой метрике g{\displaystyle g} (отличающейся от расстояния на поверхности как геометрической форме, учитывающей неизотропность её электрических свойств). Каждая точка поверхности может служить узлом, и потому потенциал будет уже не вектором, а функцией u{\displaystyle u} на поверхности. Аналогом же матрицы проводимостей будет оператор Лапласа — Бельтрами Δg{\displaystyle \Delta _{g}} метрики-проводимости, который действует на пространстве гладких функций. Первое правило Кирхгофа для поверхности гласит ровно то же: Δgu=0{\displaystyle \Delta _{g}u=0}. Иначе говоря, потенциал есть гармоническая функция.

В связи с этим матрицу A{\displaystyle A}, сопоставляемую произвольному взвешенному графу, за исключением диагонали равную матрице смежности, иногда называют дискретным лапласианом. Аналоги теорем о гармонических функциях, такие как существование гармонической функции в области с краем при заданных значениях на крае, получающейся свёрткой с некоторым ядром, имеют место и для дискретных гармонических функций. Обратно, проводящая поверхность может быть приближена сеткой сопротивлений, и дискретные гармонические функции на этой сетке приближают гармонические функции на соответствующей поверхности. На этом обстоятельстве основан интегратор Гершгорина, аналоговая вычислительая машина, использовавшаяся для решения уравнения Лапласа в 30-х — 70-х годах XX века.

В случае проводящей поверхности вместо разности потенциалов имеет смысл говорить об 1-форме du{\displaystyle du}. Связанное с ней при помощи метрики-проводимости векторное поле gradg(u){\displaystyle \mathrm {grad} _{g}(u)} — и есть электрический ток на этой поверхности. Согласно первому правилу Кирхгофа, эта 1-форма тоже гармонична (то есть лежит в ядре ходжева лапласиана, определённого на дифференциальных формах). Это даёт ключ к тому, как правильно формулировать закон Кирхгофа для случая, когда поле не потенциально: именно, 1-форма, получающаяся из тока, рассматриваемого как векторное поле, при помощи проводимости, рассматриваемой как риманова метрика, должна быть гармонична. Зная электродвижущую силу вокруг каждого топологически нетривиального контура на поверхности, можно восстановить силу и направление тока в каждой точке, притом единственным способом. В частности, размерность пространства всевозможных токов равна размерности пространства топологически нетривиальных контуров. Этот факт был одним из оснований для открытия двойственности Пуанкаре; то обстоятельство, что электродвижущие силы определяют однозначно ток (гармоническую 1-форму), является частным случаем теории Ходжа для 1-форм (теория Ходжа утверждает, что на римановом многообразии всякий класс когомологий де Рама представляется гармонической формой, притом только одной).

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Электрическая цепь — это… Что такое Электрическая цепь?

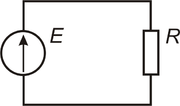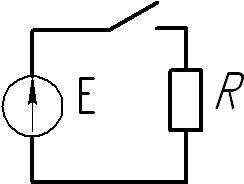
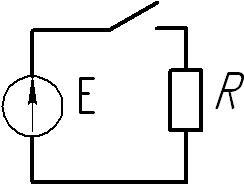
Рисунок 1 — Условное обозначение электрической цепи

Электри́ческая цепь  — совокупность устройств, элементов, предназначенных для протекания электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий сила тока и напряжение.

Изображение электрической цепи с помощью условных знаков называют электрической схемой (рисунок 1).

Классификация электрических цепей

Неразветвленные и разветвленные электрические цепи

Рисунок 2 — Разветвленная цепь

Электрические цепи подразделяют на неразветвленные и разветвленные. На рисунке 1 представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рисунке 2. В ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь узел есть точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рисунок 2), то в этом месте есть электрическое соединение двух линий, в противном случае его нет. Узел, в котором сходятся две ветви, одна из которых является продолжением другой, называют устранимым или вырожденным узлом

Линейные и нелинейные электрические цепи

Линейной электрической цепью называют такую цепь, все компоненты которой линейны. К линейным компонентам относятся зависимые и независимые идеализированные источники токов и напряжений, резисторы (подчиняющиеся закону Ома), и любые другие компоненты, описываемые линейными дифференциальными уравнениями, наиболее известны электрические конденсаторы и индуктивности. Если цепь содержит отличные от перечисленных компоненты, то она называется нелинейной.

Изображение электрической цепи с помощью условных обозначений называют электрической схемой. Функция зависимости тока, протекающего по двухполюсному компоненту от напряжения на этом компоненте называют вольт-амперной характеристикой (ВАХ). Часто ВАХ изображают графически в декартовых координатах. При этом по оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.

В частности, омические резисторы, ВАХ которых описывается линейной функцией и на графике ВАХ являются прямыми линиями, называют линейными.

Примерами линейных (как правило, в очень хорошем приближении) цепей являются цепи, содержащие только резисторы, конденсаторы и катушки индуктивности без ферромагнитных сердечников.

Некоторые нелинейные цепи можно приближенно описывать как линейные, если изменение приращений токов или напряжений на компоненте мало, при этом нелинейная ВАХ такого компонента заменяется линейной (касательной к ВАХ в рабочей точке). Этот подход называют «линеаризацией». При этом к цепи может быть прменён мощный математический аппарат анализа линейных цепей. Примерами таких нелинейных цепей, анализируемых как линейные относятся практически любые электронные устройства, работающие в линейном режиме и содержащие нелинейные активные и пассивные компоненты (усилители, генераторы и др.).

Законы, действующие в электрических цепях

См. также

Литература

• Электротехника: Учеб. для вузов/А. С. Касаткин, М. В. Немцов.— 7-е изд., стер.— М.: Высш. шк., 2003.— 542 с.: ил. ISBN 5-06-003595-6
• Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. — М.: Гардарики, 2002. — 638 с. — ISBN 5-8297-0026-3

Ссылки