4. Потери и падения напряжения в электрических сетях
Рассмотрим линию электропередачи, по которой протекает ток I и передается мощность S, а напряжения в начале (со стороны источника питания) и в конце (со стороны нагрузки) соответственно равны U1 и U2 (рис. 4.1).
Падением
напряжения называется
разность комплексов напряжений в начале
и в конце элемента сети (в данном случае
линии)  .
.
Потерей
напряжения называется
разность модулей напряжений в начале
и в конце элемента сети 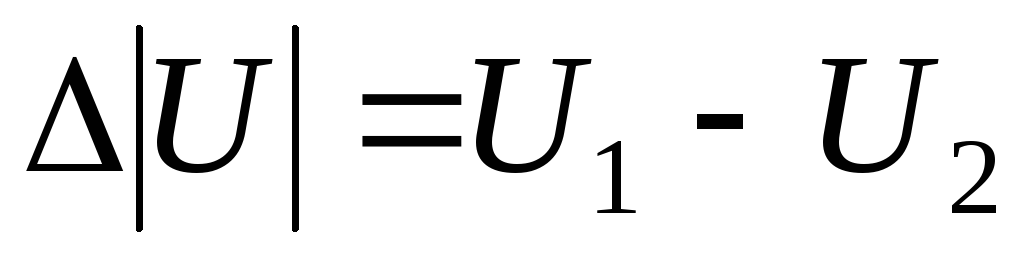 .
.
Падение напряжения – величина векторная, а потеря напряжения – скалярная.
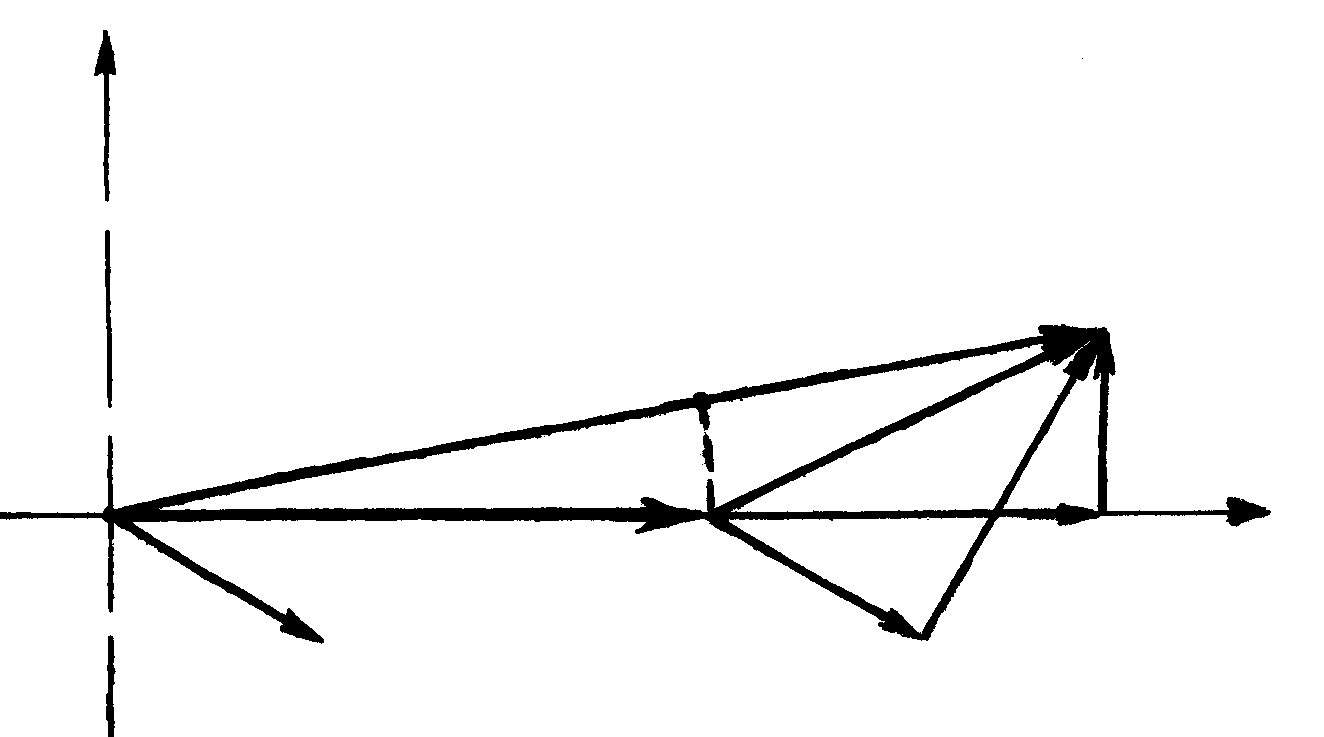
На рис. 4.2 изображена векторная диаграмма линии (емкостные токи не показаны). Напряжения на этой диаграмме по модулю равны линейным, а по фазе – фазным. Фактически это линейные напряжения, фазы которых изменены на 30°. Такие напряжения используются во всех дальнейших выкладках и расчетах.
Zл

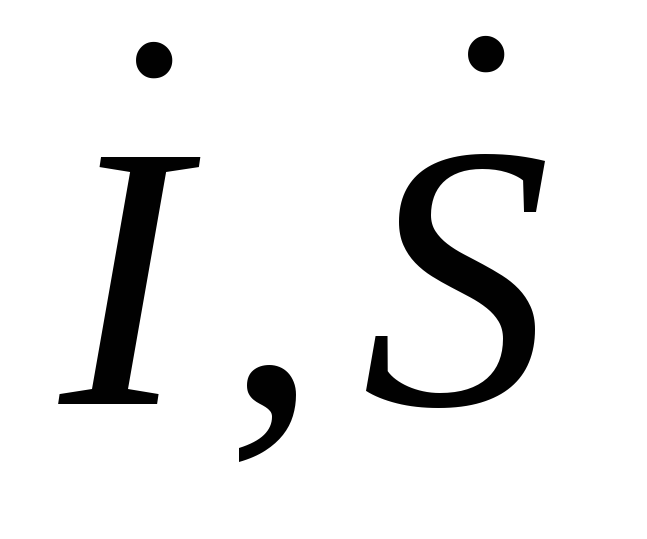
Р
Bл
Bл
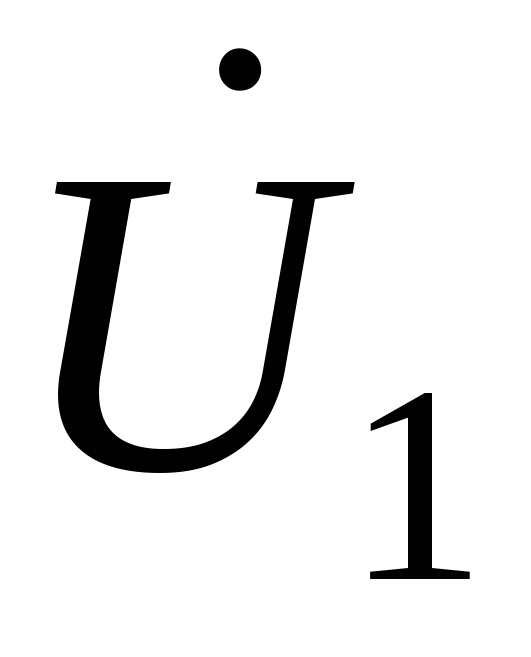

расчета падения и потери напряжения
+j
D
C


+1
A
B
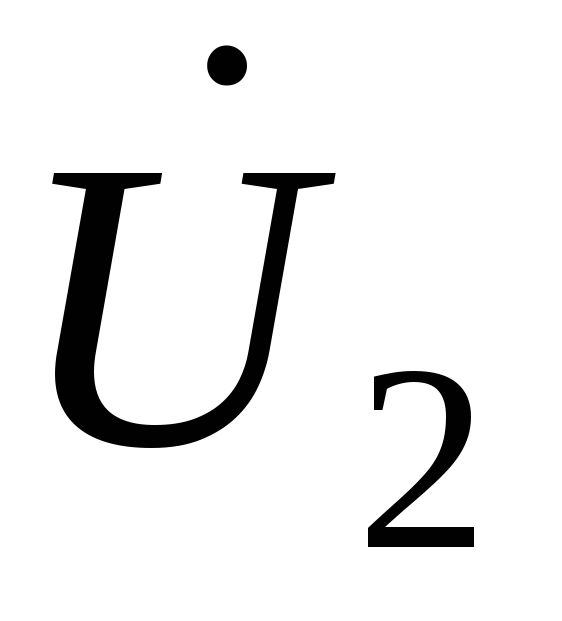
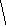
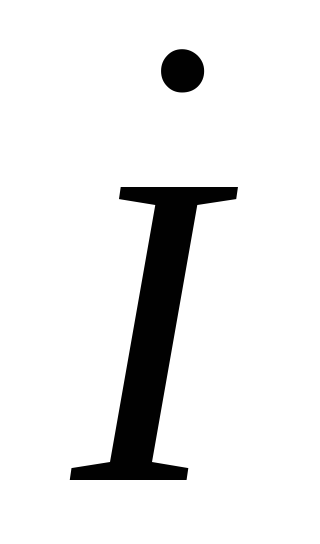
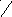

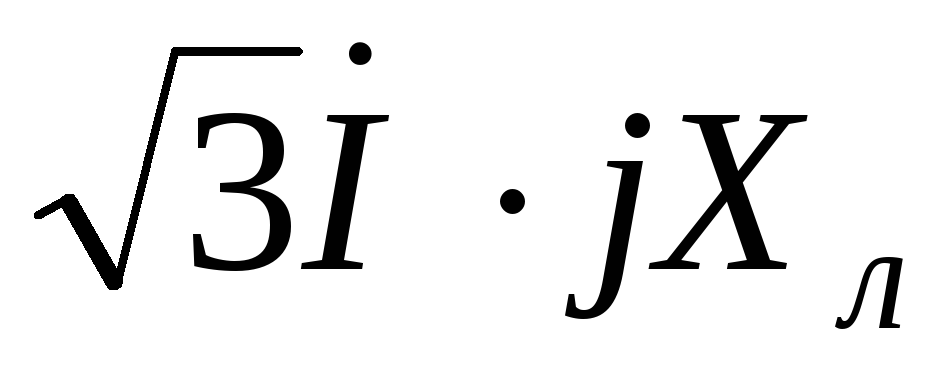
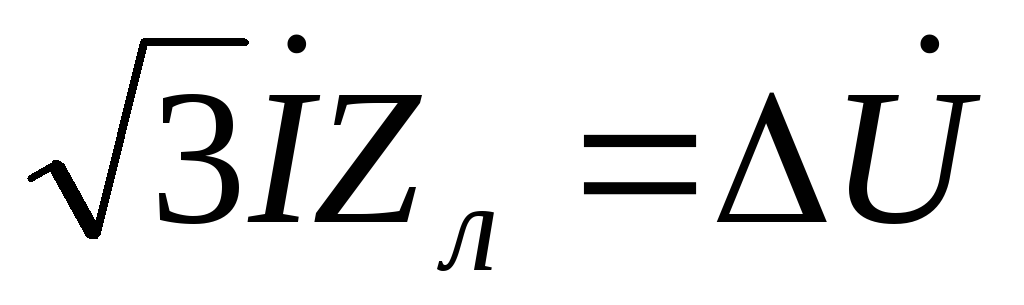
Рис. 4.2. Векторная диаграмма линии электропередачи
Построение
векторной диаграммы начинается с
векторов  и
и 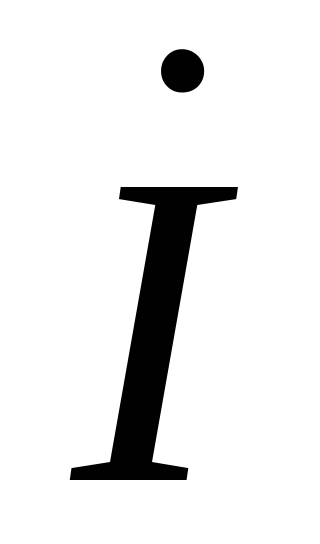 при условии,
что ток имеет активно-индуктивный
характер. Затем строятся падения
напряжения на активном, реактивном и
полном сопротивлении линии
при условии,
что ток имеет активно-индуктивный
характер. Затем строятся падения
напряжения на активном, реактивном и
полном сопротивлении линии 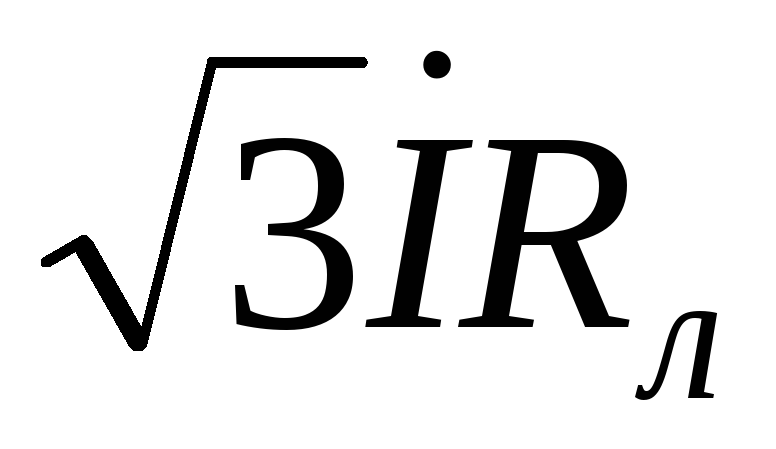
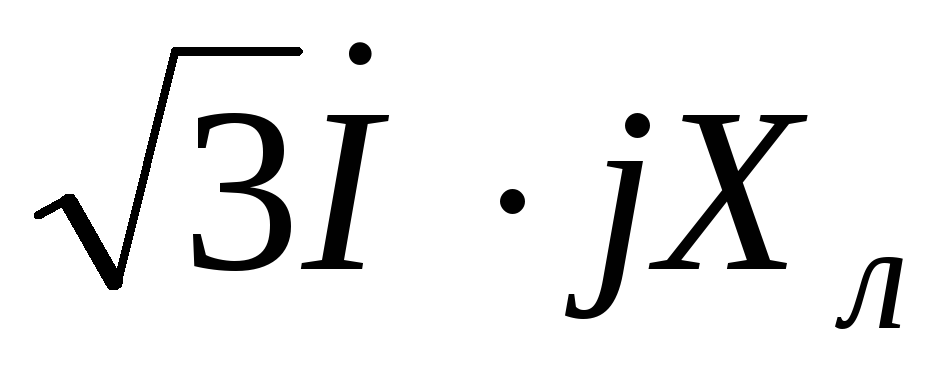 и
и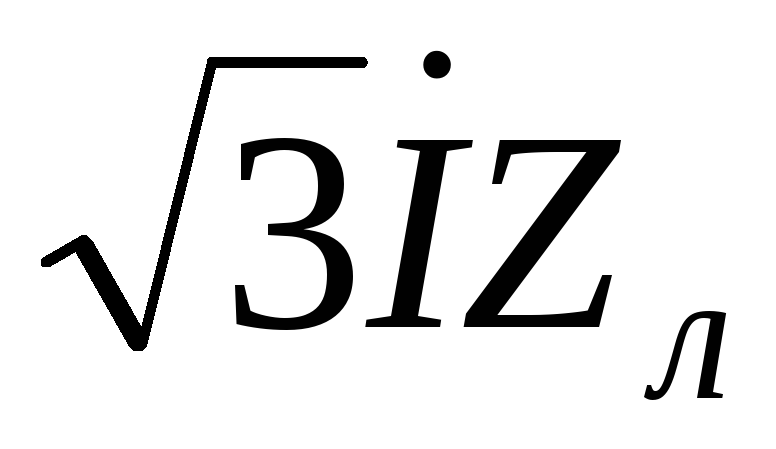 . Прибавив
последний вектор к
. Прибавив
последний вектор к 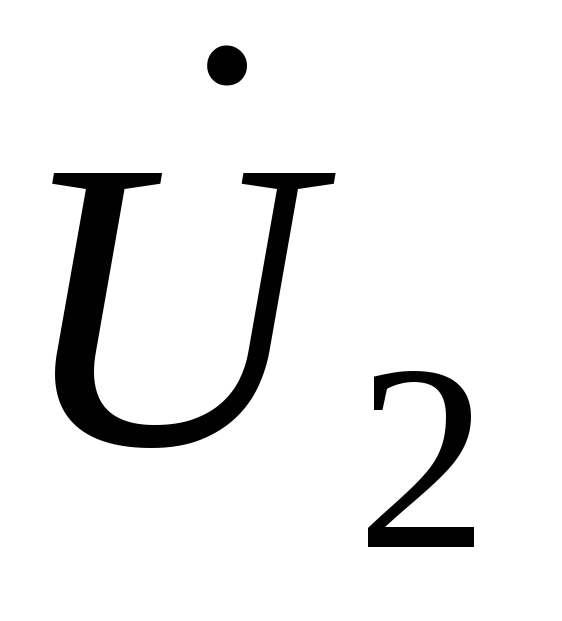 ,
получим напряжение в начале линии
,
получим напряжение в начале линии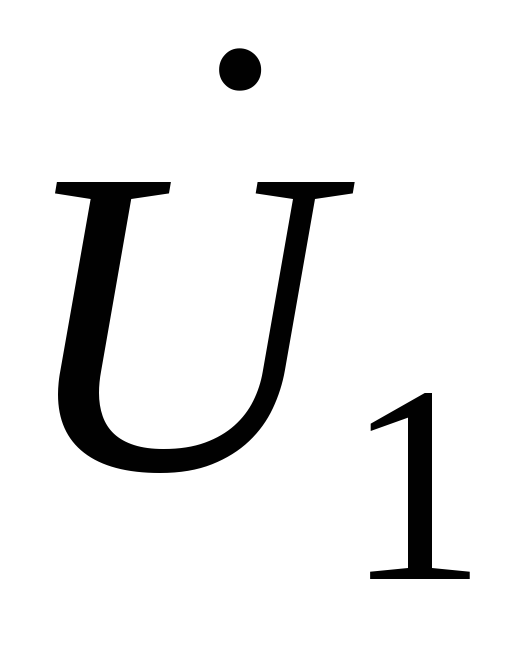 .
. Вектор 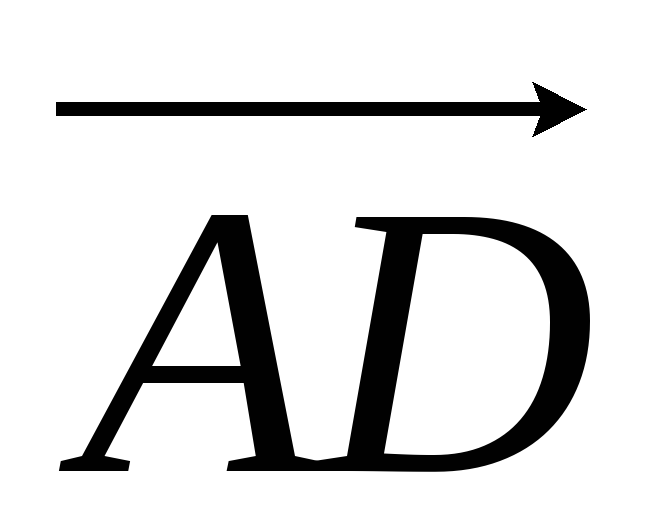 представляет собой падение напряжения
в линии
представляет собой падение напряжения
в линии  ,
а отрезокCD
– потерю напряжения
,
а отрезокCD
– потерю напряжения 
 до совмещения
с вектором
до совмещения
с вектором  .
.Выразим падение напряжения через передаваемую мощность, которая связана с током соотношением
 .
(4.1)
.
(4.1)
Верхний индекс «*» здесь и далее обозначает сопряженные комплексы.
Из (4.1) при нулевой фазе напряжения следует
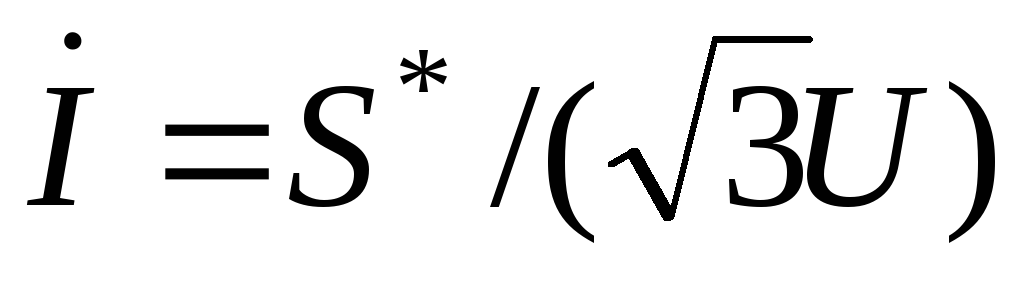 .
(4.2)
.
(4.2)
Тогда
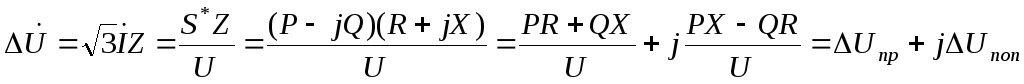
где U – напряжение, в качестве которого может быть принято напряжение либо в начале, либо в конце данного элемента сети (при приближенных расчетах может использоваться также номинальное напряжение).
Величина
ΔUnp называется
продольной составляющей падения
напряжения и представляет собой
действительную часть падения напряжения
(вектор 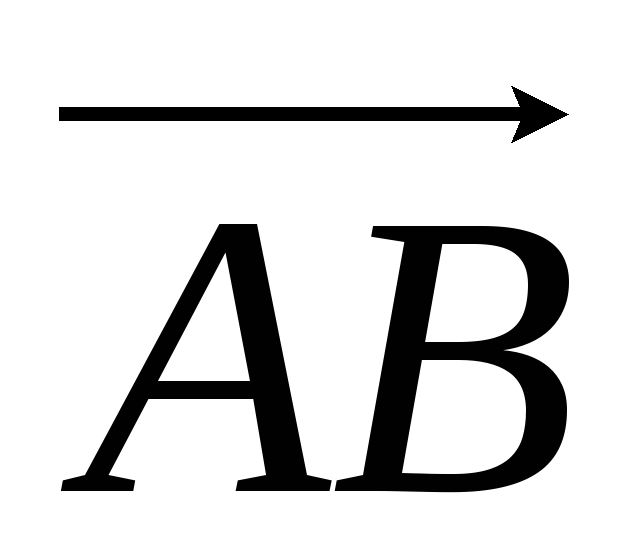 на рис. 4.2).
на рис. 4.2).
Величина
ΔUnon называется
поперечной составляющей падения
напряжения и представляет собой мнимую
часть падения напряжения (вектор 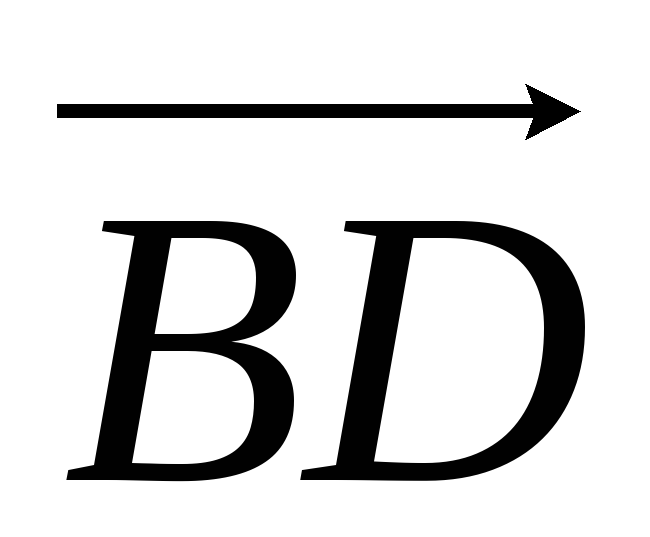 ).
).
Значения
продольной и поперечной составляющей
падения напряжения зависят от того,
через какое напряжение они рассчитаны.
В случае, рассмотренном на рис. 4.2, этим
напряжением является
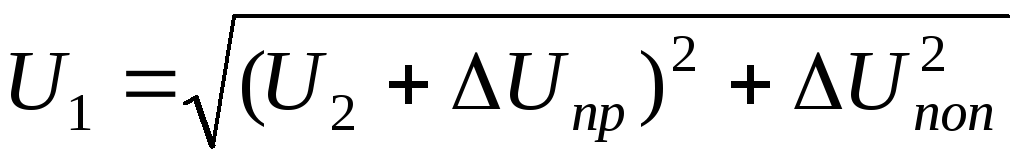 ,
(4.4)
,
(4.4)
 . (4.5)
. (4.5)
С практической точки зрения модуль напряжения более важен, чем его фаза. Поэтому в некоторых случаях поперечная составляющая падения напряжения может не учитываться, так как она изменяет главным образом только фазу. При таком допущении потеря и падение напряжения равны друг другу.
3.4. Падение и потеря напряжения в линии
На рис.
3.2, е приведена векторная диаграмма для
ли-
нейных
напряжений в начале и в конце линии  и
и  . Эта
диаграмма
аналогична диаграмме на рис.
3.2, в.
. Эта
диаграмма
аналогична диаграмме на рис.
3.2, в.
Падение
напряжения—геометрическая
(векторная)
разность
между комплексами напряжений начала и
конца
линии.
На рис.
3.2, е падение напряжения
— это
вектор  , т. е.
, т. е.
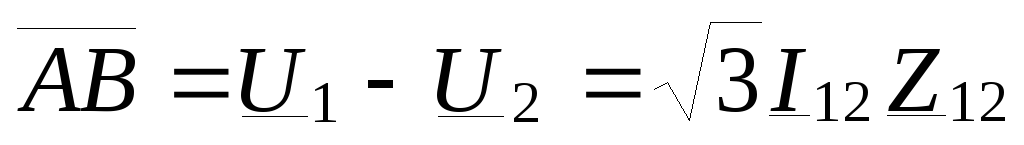 .
(3.26)
.
(3.26)
Продольной
составляющей падения напряжения называют
проекцию падения напряжения на
действитель-
ную
ось или на напряжение 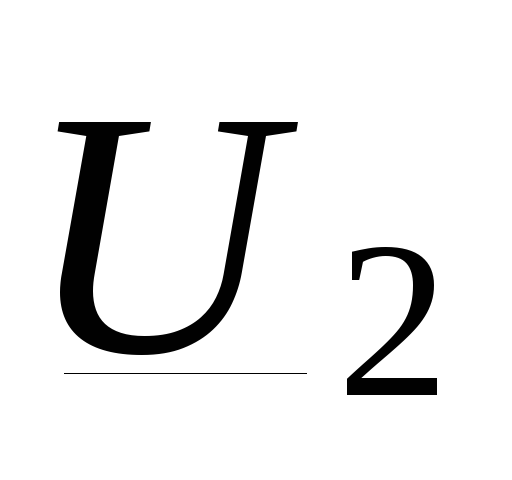
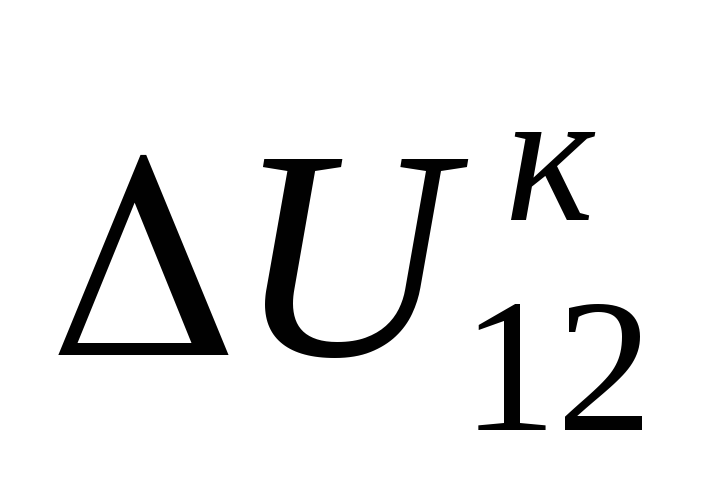 =АС
на рис.
3.2, е. Индекс
«к» означает, что
=АС
на рис.
3.2, е. Индекс
«к» означает, что  — проекция
на напряжение
конца
линии
— проекция
на напряжение
конца
линии 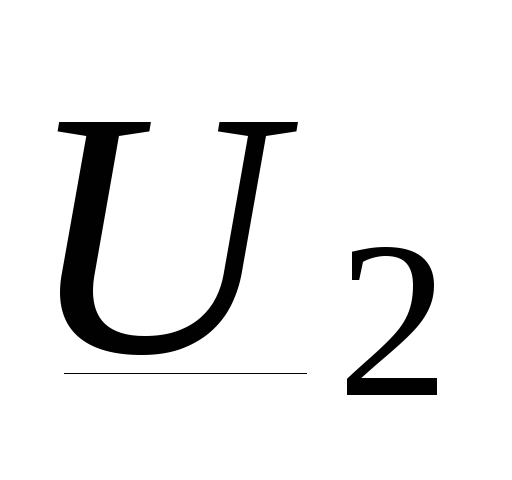 . Обычно
. Обычно 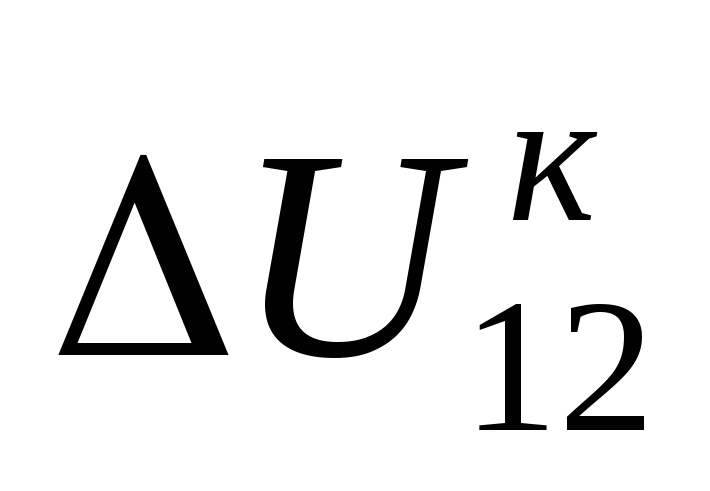 выражается через данные в конце
линии:
выражается через данные в конце
линии: 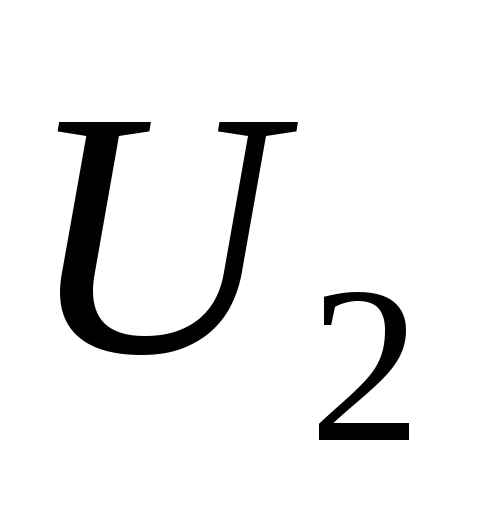 ,
,  ,
,  .
. Поперечная
составляющая падения напряжения 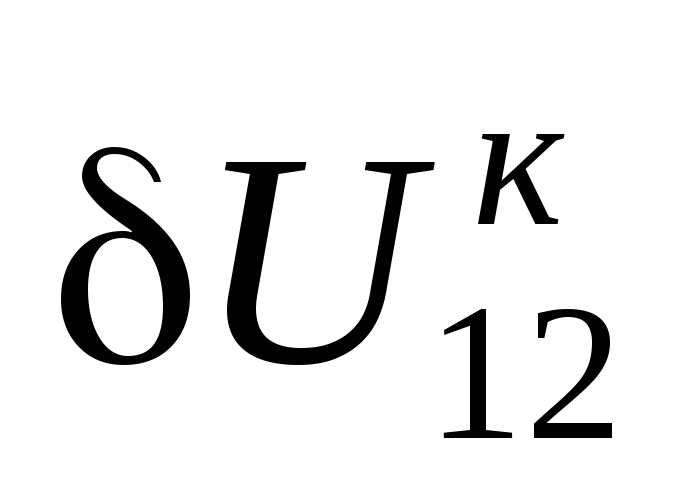
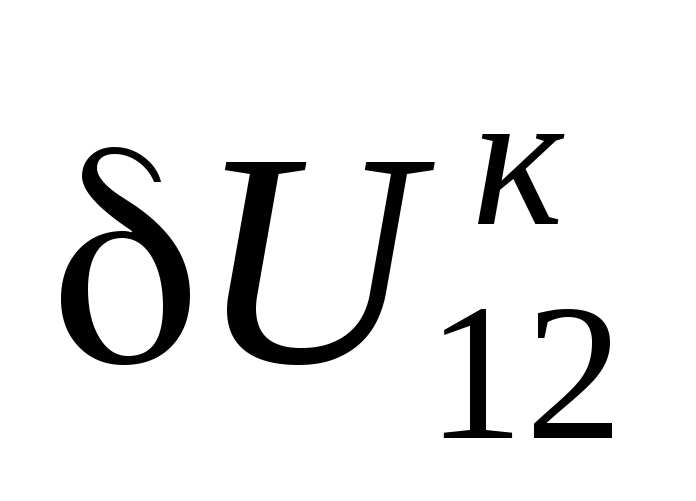 ==СВ на рис.
3.2, е. Таким образом,
==СВ на рис.
3.2, е. Таким образом, 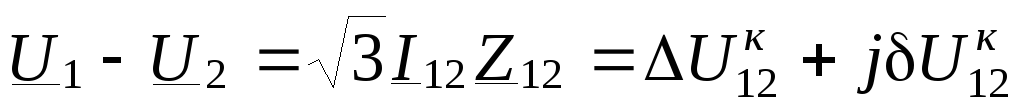 .
(3.27)
.
(3.27)
Часто используют
понятие потеря
напряжения — это
ал-
гебраическая
разность между модулями напряжений
на-
чала
и конца линии. На рис. 3.2,е 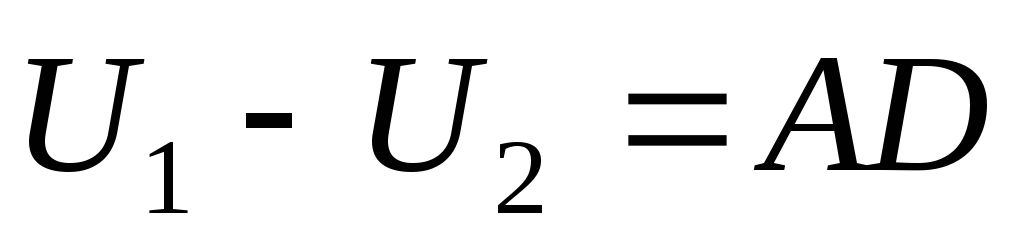 . Если попе-
речная
составляющая
. Если попе-
речная
составляющая 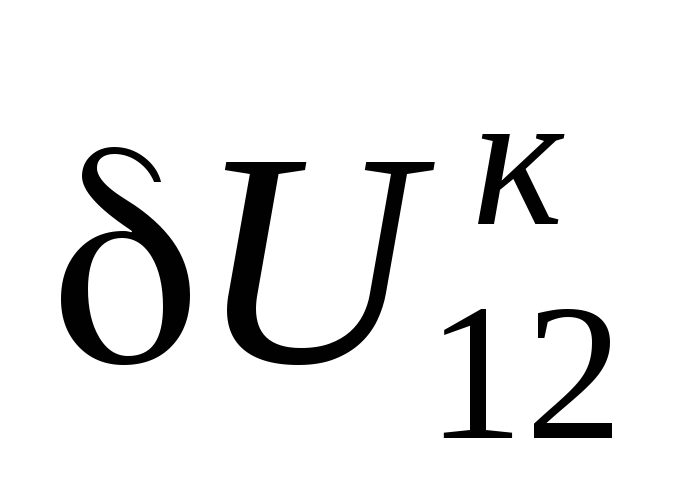 мала (например, в сетях
мала (например, в сетях 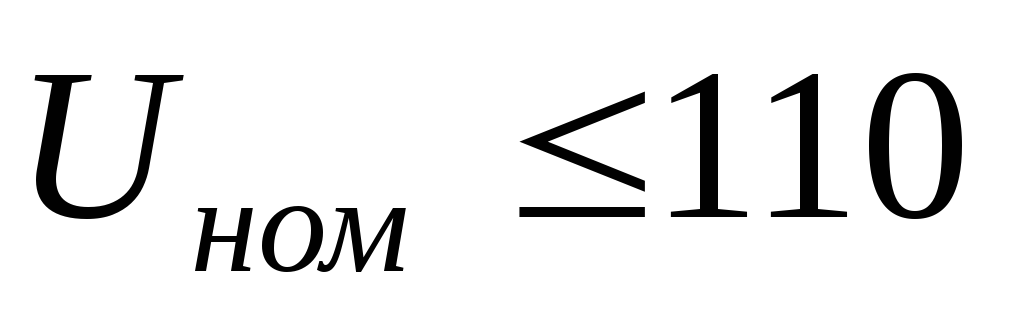 кВ), то можно приближенно считать, что
потеря
напряжения
равна продольной составляющей падения
на-
пряжения.
кВ), то можно приближенно считать, что
потеря
напряжения
равна продольной составляющей падения
на-
пряжения.
Расчет режимов электрических сетей ведется в мощно- стях, поэтому выразим падение напряжения и его состав- ляющие через потоки мощности в линии.
Известны
мощность и напряжение в конце линии (рас-
чет
напряжения в начале линии по данным
конца). Выра-
зим
ток в линии 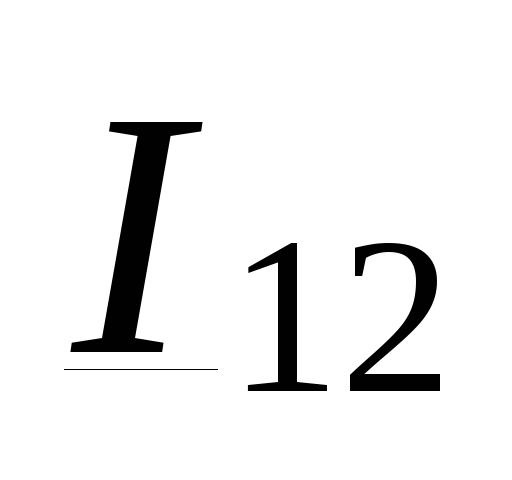 в
(3.27) через
мощность в конце про-
дольной
части линии
в
(3.27) через
мощность в конце про-
дольной
части линии  и напряжение
и напряжение 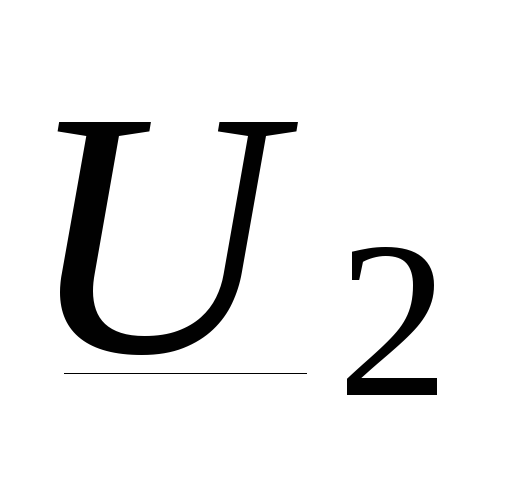 :
:
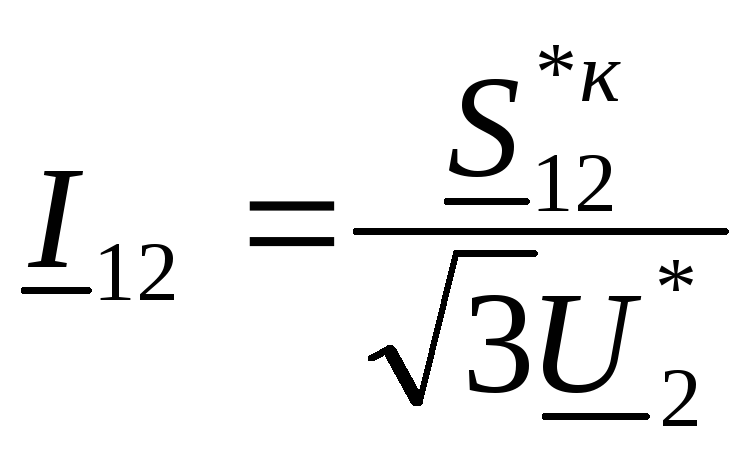 .
(3
28)
.
(3
28)
В результате получим
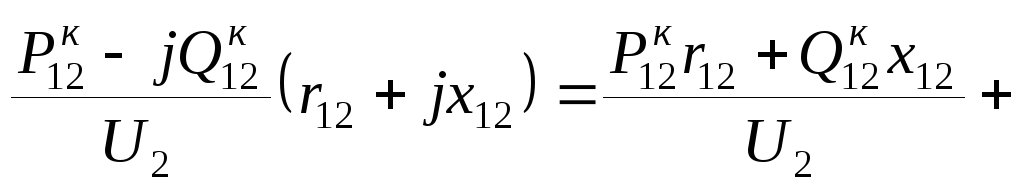
 .
(3.29)
.
(3.29)
Приравняв в (3.29) действительные и мнимые части, по- лучим выражения продольной и поперечной составляющих падения напряжения по данным конца:
 ;
(3.30)
;
(3.30)
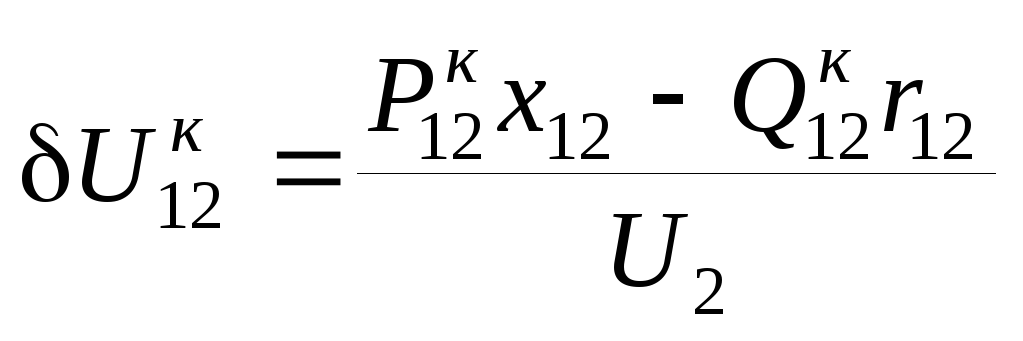 .
(3.31)
.
(3.31)
Напряжение в начале линии
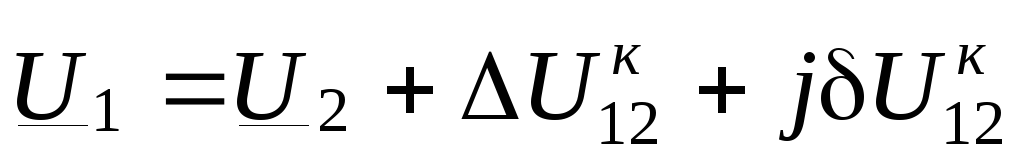 ,
(3.32)
,
(3.32)
где 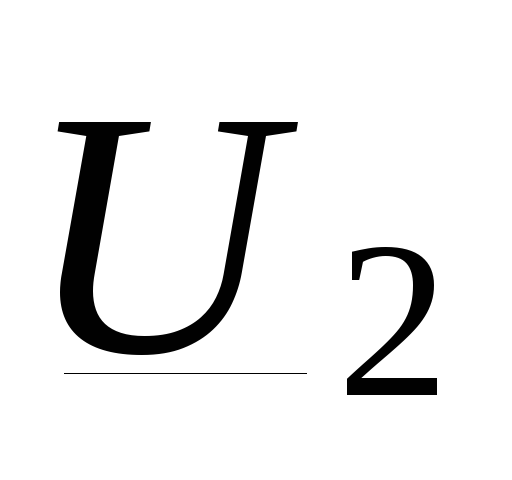 известно;
известно;  ,
, 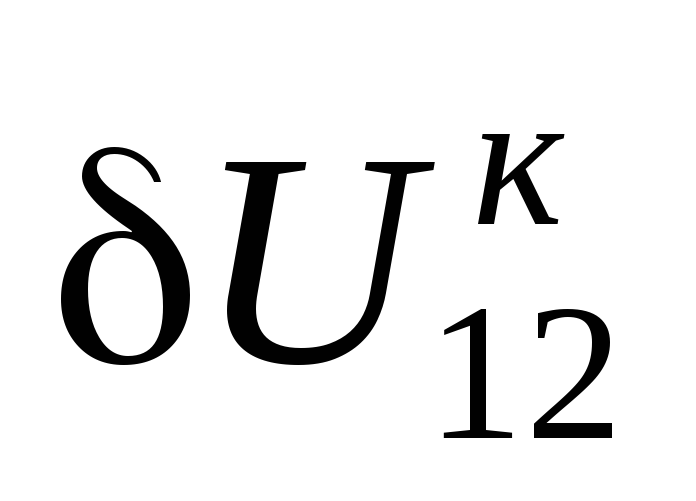 определяем из
(3.30) и
(3.31).
определяем из
(3.30) и
(3.31).
Соответственно модуль и фаза напряжения в начале ли- нии (см. рис. 3.2, е)
 ;
(3.33)
;
(3.33)
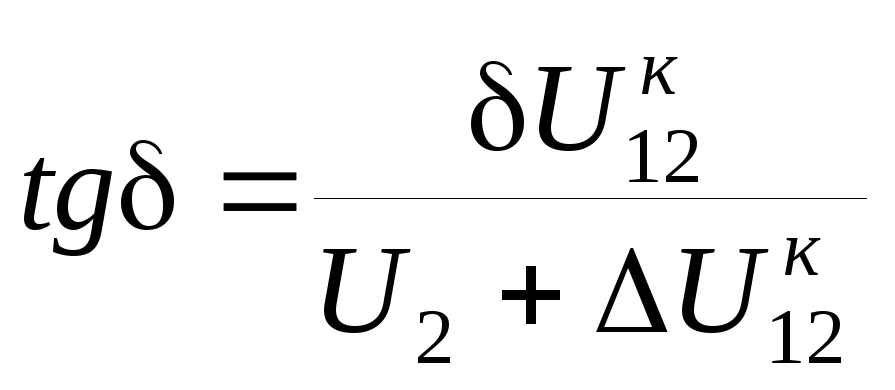 .
(3.34)
.
(3.34)
Определение напряжения в начале линии по данным конца по выражениям (3.32), а также (3.30), (3.31) экви- валентно использованию закона Ома.
Пример 3.2. Определим падение и потерю напряжения
в линии, рас-
смотренной
в примере
3.1, по
известным мощности нагрузки  =15+
+j10
МВА
и напряжению в конце линии
=15+
+j10
МВА
и напряжению в конце линии 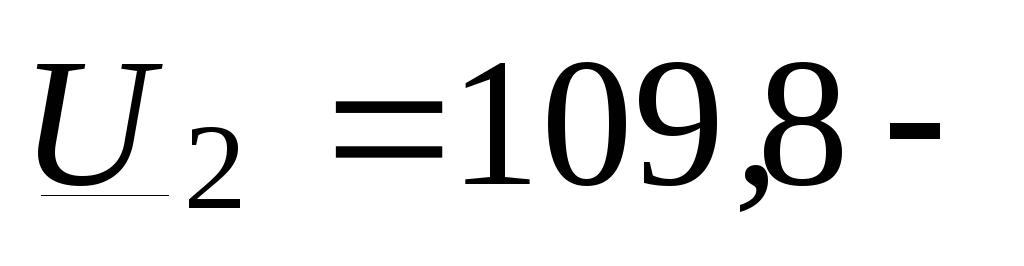 j2,65
кВ.
j2,65
кВ.
Используя параметры
линии, а также мощность в конце линии 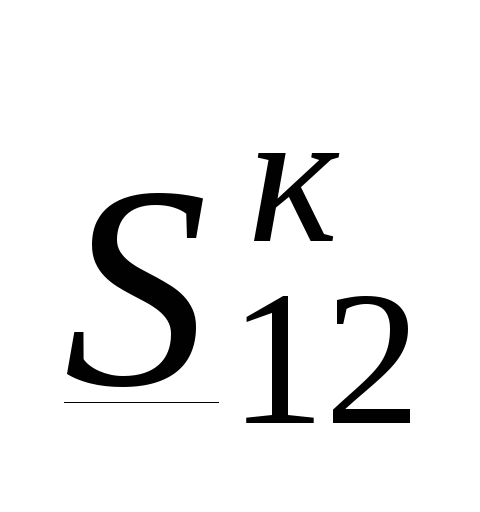 ,
приведенные в примере
3.1, по
(3.30), (3.31)
найдем продольную
и
поперечную составляющие падения
напряжения по данным конца:
,
приведенные в примере
3.1, по
(3.30), (3.31)
найдем продольную
и
поперечную составляющие падения
напряжения по данным конца:
 кВ
;
кВ
;
 кВ
.
кВ
.
Напряжения  и
и приведены на рис.
3.2, з.
В большем мас-
штабе
продольная и поперечная составляющие
падения напряжения
изображены
на рис
3.2, и.
приведены на рис.
3.2, з.
В большем мас-
штабе
продольная и поперечная составляющие
падения напряжения
изображены
на рис
3.2, и.
Напряжение в начале линии по (3.32) равно
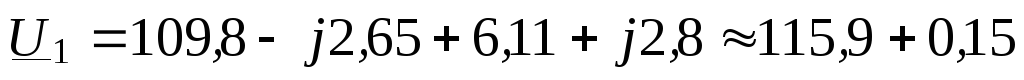 кВ.
кВ.
Модуль напряжения в начале линии
 кВ.
кВ.
Потеря напряжения
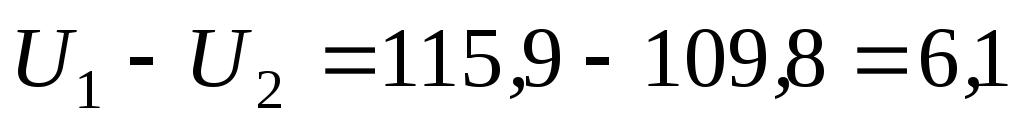 кВ.
кВ.
Известны
мощность и напряжение в начале линии (рас-
чет
напряжения в конце линии по данным
начала). Напра-
вим  по действительной оси, т.е.
примем, что
по действительной оси, т.е.
примем, что 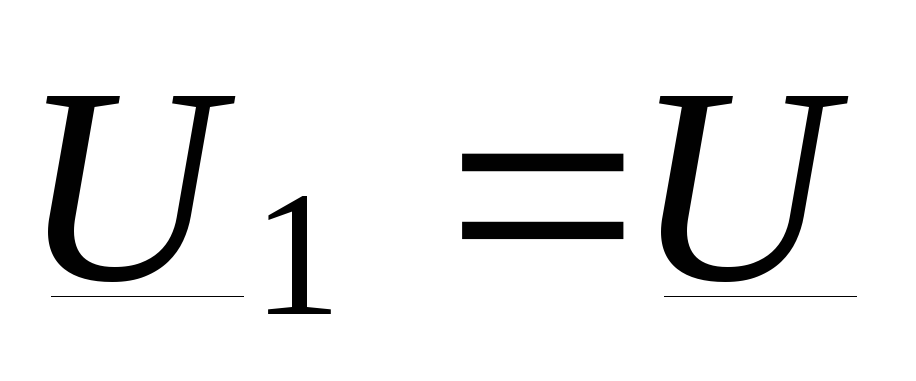 (рис.
3.2, ж).
На рис. 3.2, ж изменилось
положение осей
в
сравнении с рис.
3.2, е.
Продольная составляющая паде-
ния
напряжения
(рис.
3.2, ж).
На рис. 3.2, ж изменилось
положение осей
в
сравнении с рис.
3.2, е.
Продольная составляющая паде-
ния
напряжения  =ВС‘—это
проекция падения на-
пряжения
на действительную ось или на
=ВС‘—это
проекция падения на-
пряжения
на действительную ось или на 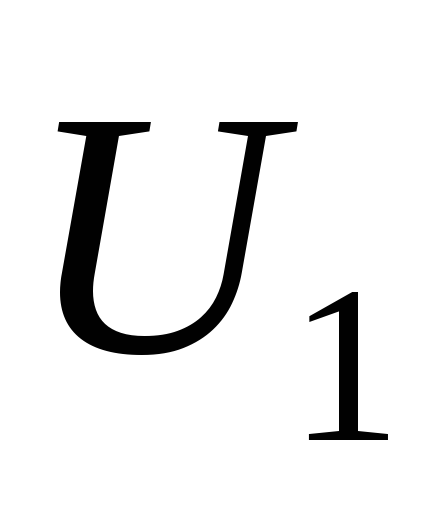 . Поперечная
составляющая
падения напряжения
. Поперечная
составляющая
падения напряжения  =АС’—это
про-
екция
падения напряжения на мнимую ось. Один
и тот же
вектор
падения напряжения
=АС’—это
про-
екция
падения напряжения на мнимую ось. Один
и тот же
вектор
падения напряжения  проектируется на различ-
ные
оси. Поэтому
проектируется на различ-
ные
оси. Поэтому
 ,
, .
.
Если выразить ток
в линии 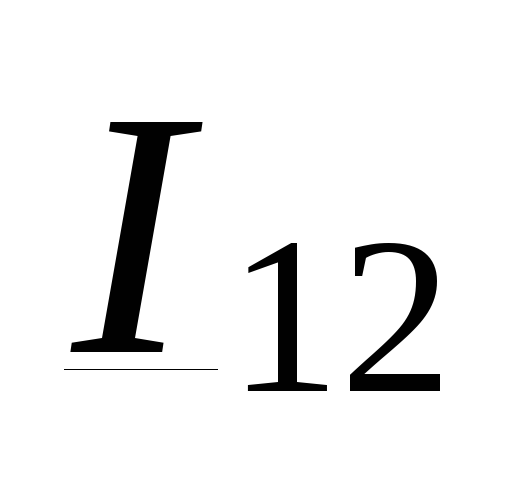 аналогично
(3.28) через известные
в данном случае мощность в начале
продольной
ветви
линии
аналогично
(3.28) через известные
в данном случае мощность в начале
продольной
ветви
линии 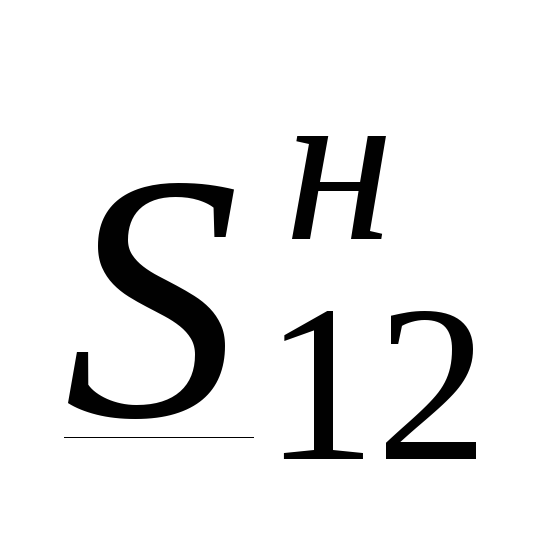 и
и 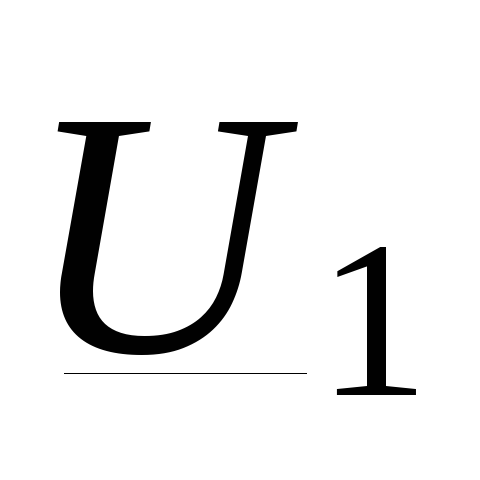 , то
получим
выражения, аналогичные
(3.30),
(3.31):
, то
получим
выражения, аналогичные
(3.30),
(3.31):
 ;
(3.35)
;
(3.35)
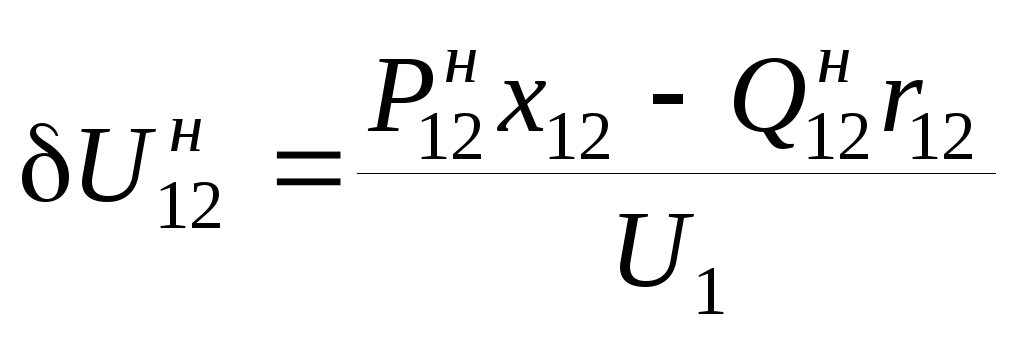 .
(3.36)
.
(3.36)
Напряжение в конце линии
 , (3.37)
, (3.37)
где  известно;
известно;  ,
,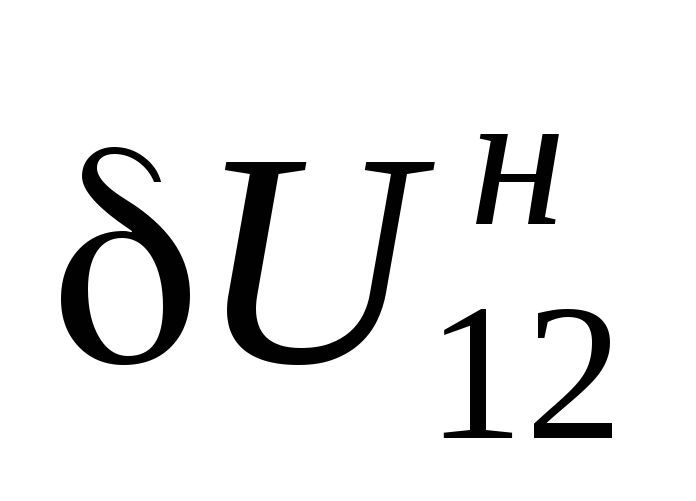 определяются
из(3.35),
(3.36).
Модуль
и фаза
определяются
из(3.35),
(3.36).
Модуль
и фаза 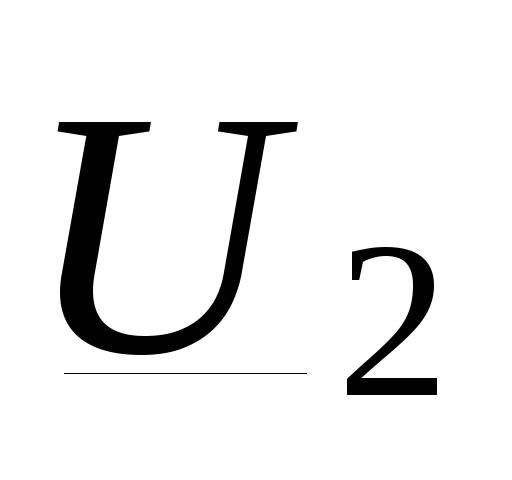 равны
равны
 ;
(3.38)
;
(3.38)
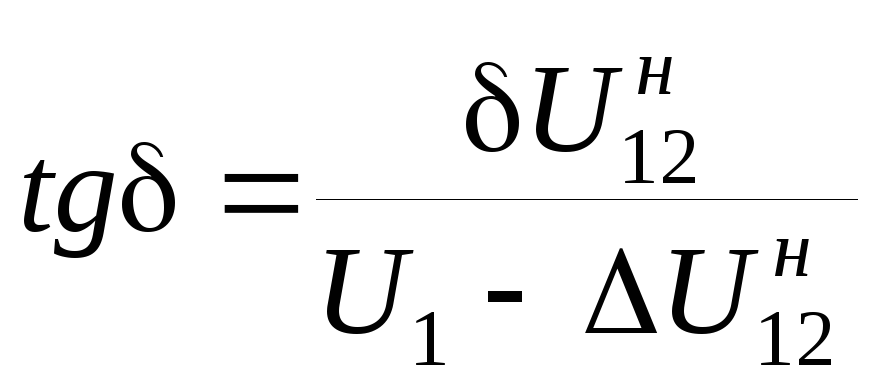 .
(3.39)
.
(3.39)
Определение напряжения в конце линии по данным на- чала по выражениям (3.37), а также (3.35), (3.36) эквива- лентно применению закона Ома в виде (3.25).
Пример 3.3. Определим падение и потерю напряжения
в линии, рассмотренной
в примере
3.1, по
известным мощности в начале линии  =15,61+j9,6
МВА
и напряжению в начале линии
=15,61+j9,6
МВА
и напряжению в начале линии 
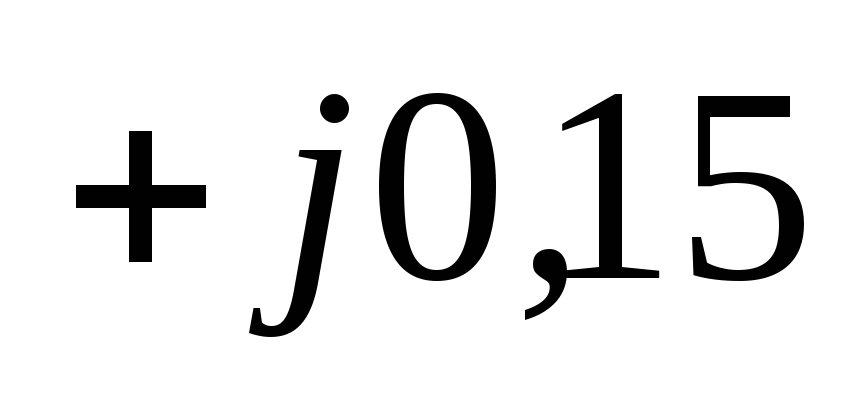 кВ;
кВ; 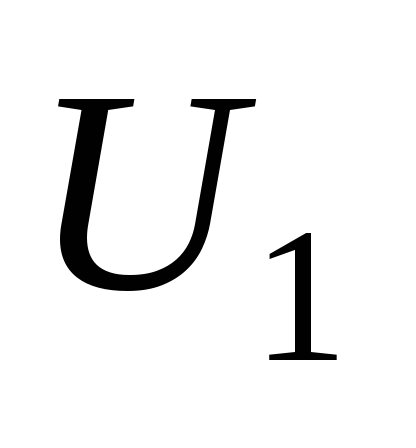 = 115,9 кВ.
= 115,9 кВ.
Используя параметры линии, приведенные в примере 3.1, по выра- жениям (3.35), (3.36) найдем продольную и поперечную составляющие падения напряжения по данным начала:
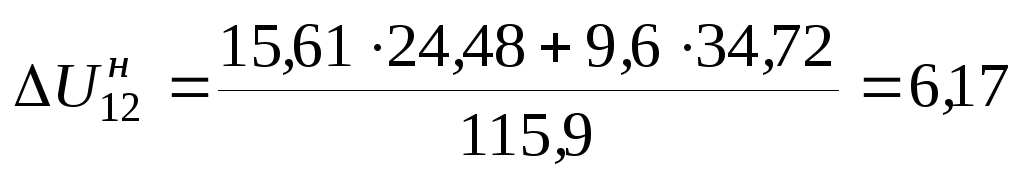 кВ:
кВ:
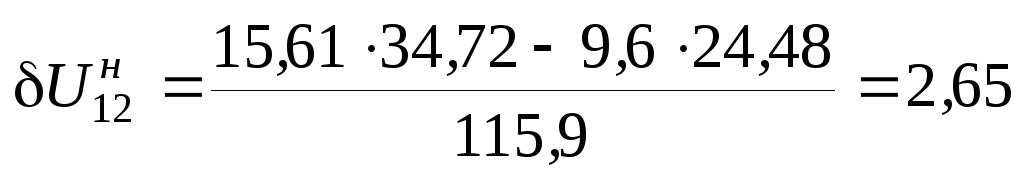 кВ.
кВ.
Напряжение в конце линии по (3.37)
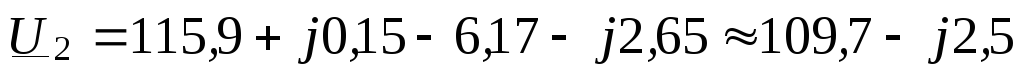 кВ.
кВ.
Модуль напряжения в конце линии
 кВ.
кВ.
Потеря напряжения  кВ.
кВ.
Результаты
определения напряжений в примерах
3.1, 3.2 и
3.3
раз-
личаются
на погрешность округления, в примере
3.1 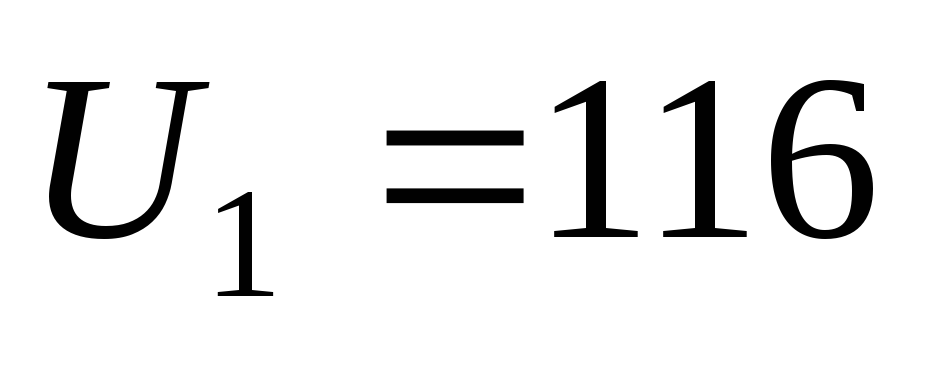 кВ, а в
примере
3.2
кВ, а в
примере
3.2 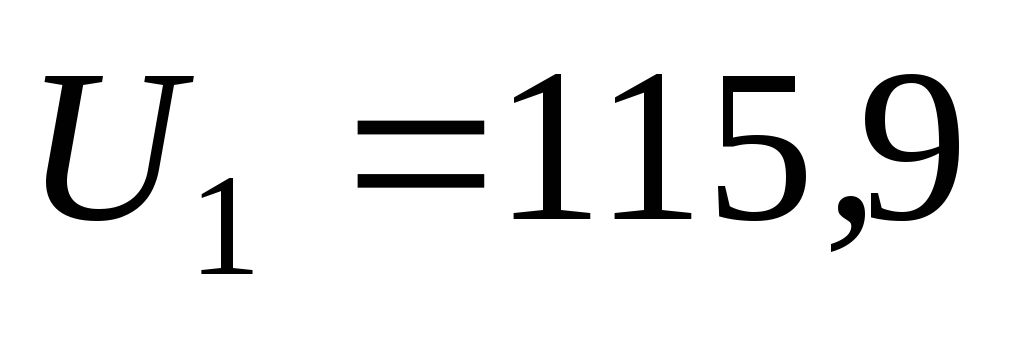 кВ. Соответственно в примерах
3.2, 3.3 потери напряжения
равны
6,1 и
6,2 кВ. При
проведении расчетов напряжений
с
четырьмя значащими цифрами погрешность
округления при опреде-
лении,
например,
кВ. Соответственно в примерах
3.2, 3.3 потери напряжения
равны
6,1 и
6,2 кВ. При
проведении расчетов напряжений
с
четырьмя значащими цифрами погрешность
округления при опреде-
лении,
например, 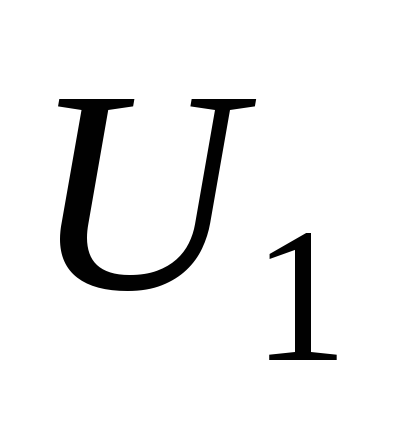 в данных примерах равна
116—115,9=0,1
кВ. Ес-
ли
проводить расчеты с восемью значащими
цифрами, то результаты
определения
в данных примерах равна
116—115,9=0,1
кВ. Ес-
ли
проводить расчеты с восемью значащими
цифрами, то результаты
определения 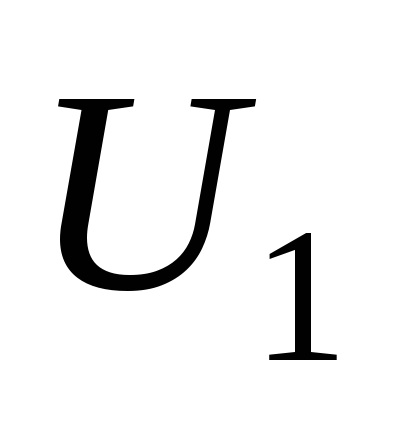 и
и  различаются
на
0,00094 кВ, т.
е.
погрешность ок-
ругления
равна
0,001 кВ.
различаются
на
0,00094 кВ, т.
е.
погрешность ок-
ругления
равна
0,001 кВ.
§12.4. Падение и потеря напряжения в линиях электроснабжения

ущерб (доменные цехи, котельные производственного пара, подъемные и вентиляционные установки шахт, аварийное освещение и др.). Они должны работать непрерывно. Для потребителей второй категории (самых многочисленных) допускаются перерывы в питании на ограниченное время. К потребителям третьей категории относятся вспомогательные цехи и другие объекты, для которых допускается перерыв в электроснабжении до одних суток.
Для повышения надежности энергоснабжения предусматривается питание потребителей от двух независимых сетей и автоматически включаемого резервного источника электроэнергии. Различают «горячий» и «холодный» резервные источники. «Горячий» резервный источник обеспечивает немедленное аварийное питание, его используют для безаварийной остановки потребителя.
Дальнейшее улучшение систем электроснабжения промышленных предприятий связано с повышением напряжения питания (с 220 до 380В, с 6 до 10кВ и т.д.) при максимально возможном приближении высокого напряжения к потребителям (глубокий ввод) и уменьшении числа ступеней трансформации.
Карточка № 12.3 (220).
Электроснабжение промышленных предприятий
Что составляет основу ЕЭС СССР? | ТЭС |
|
| 35 |
| ГЭС |
|
| 148 |
| АЭС |
|
| 69 |
| ЛЭП |
|
| 178 |
|
|
| ||
Какое свойство не относится к достоинствам ЕЭС? | Надежность питания потребителей | 94 | ||
| Возможность менять | направление | 13 | |
| потоков энергии в течение суток |
| ||
|
|
| ||
| Постоянство напряжения и частоты | 63 | ||
|
|
| ||
| Возможность получения высоких и | 243 | ||
| сверхвысоких напряжений |
| ||
|
|
|
|
|
Какое напряжение допустимо в особо опасных | 660В |
|
| 29 |
условиях? |
|
|
|
|
36В |
|
| 185 | |
| 12В |
|
| 27 |
| 380/220В |
|
| 219 |
К какой категории потребителей следует отнести | К первой категории |
| 59 | |
компрессорные установки шахт? |
|
|
| |
Ко второй категории |
| 188 | ||
| К третьей категории |
| 92 | |
Какое электропитание обеспечивает безаварийную | От | резервного | источника, | 222 |
остановку агрегата? | подготовленного к запуску |
| ||
|
|
|
|
|
| От | резервного | источника, | 213 |
| работающего вхолостую |
|
| |
|
|
|
|
|
В проводах возникает падение напряжения, пропорциональное току и сопротивлению линии. Напряжение на зажимах потребителя U меньше напряжения на зажимах источника U1. Разность DU=U1—U называют потерей напряжения.
Потерю напряжения часто выражают в процентах от номинального значения напряжения потребителя: DUU ×100
При заданном напряжении источника от потери напряжения зависит напряжение на зажимах потребителя, поэтому значение потери напряжения строго регламентируется. В линиях, по которым осуществляется питание силовой (электродвигатели, гальванические ванны и др.) нагрузки, допускается потеря напряжения, не превышающая 6% от номинального напряжения потребителя. В осветительных сетях допускается потеря напряжения не более 2,5%. В

зависимости от конкретных условий могут быть установлены и другие предельные значения потери напряжения.
Несоблюдение норм потери напряжения приводит к нарушению работы потребителей, уменьшению пусковых и вращающих моментов двигателей, изменению светового потока осветительных установок. Например, при уменьшении напряжения на 10% световой поток ламп накаливания уменьшается на 1/3. Незначительное превышение напряжения относительно номинального приводит к резкому сокращению срока службы ламп накаливания.
Нетрудно видеть, что в цепях постоянного тока понятия падения и потери напряжения совпадают: U=IRпр, где I — ток в линии; Rпр — сопротивление провода линии.
Несколько сложнее выглядят эти зависимости в цепях переменного тока.
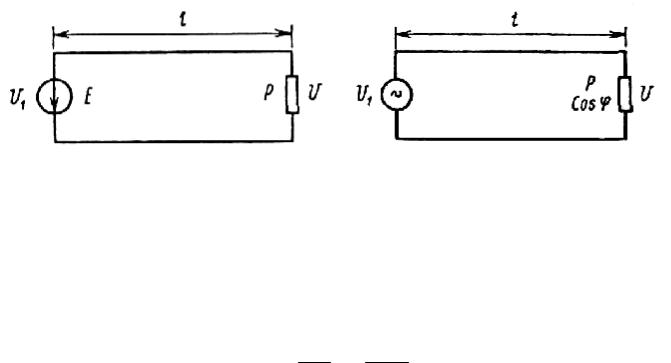
Рассмотрим векторную диаграмму токов и напряжений, изображенную на рис. 12.4. Проходящий по линии ток нагрузки I сдвинут по фазе относительно напряжения U на угол ϕ, определяемый коэффициентом мощности нагрузки. Падение напряжения на активном сопротивлении линии IR совпадает по фазе с током I, а падение напряжения на реактивном сопротивлении линии Iх опережает по фазе ток I на 90° (считаем, что емкостное сопротивление линии меньше ее индуктивного сопротивления). В этом случае падением напряжения считают
g g g
векторную разность напряжений в начале и конце линии: U =U1 −U = I Z , где Z — комплекс полного сопротивления линии.
Рис. 12.4. Связь векторов напряжений на входе и | Рис. 12.5. Приближенное выражение потери напряжения |
выходе линии | отрезком аб |
Для потребителя важно значение напряжения, поэтому целесообразно ввести понятие потери напряжения U как разности действующих значений напряжений U1 и U.
Потерю напряжения U можно выразить через модуль | g | |
вектора U . В практических | ||
расчетах принимают потерю напряжения (отрезок ас на рис. | 12.5) равной проекции вектора | |
g g | g |
|
падения напряжения U = I Z на вектор U (отрезок ab). |
| |
Рис. 12.6. Вид векторной диаграммы,если пренебречь реакт
При расчете сетей напряжением до 1000В считают, что реактивное сопротивление линии мало по сравнению с ее активным сопротивлением и им можно пренебречь. Векторная диаграмма токов и напряжений для этого случая представлена на рис. 12.6. Полагая ab≈ac, находим U≈ab=IRcosϕ, где U — потеря напряжения в линии; I — ток нагрузки, проходящий в проводах линии; R=Rпр — активное сопротивление проводов линии; cosϕ — коэффициент мощности
потребителя электроэнергии.
Карточка № 12.4 (183).
Падение и потеря напряжения в линиях электроснабжения
Напряжение на зажимах источника электроэнергии в сети | 1% |
|
| 193 | ||||
постоянного тока 26В. Напряжение на зажимах |
|
|
|
| ||||
2% |
|
| 21 | |||||
потребителя 25В. Определить потерю напряжения в |
|
|
|
| ||||
4% |
|
| 228 | |||||
процентах |
|
|
|
|
|
|
|
|
Сопротивление одного провода двухпроводной линии | 0,5В |
|
| 53 | ||||
постоянного тока 0,05Ом. Через нагрузку течет ток 10А. |
|
|
|
| ||||
1В |
|
| 200 | |||||
Рассчитать потерю напряжения |
|
|
|
|
|
| ||
|
| 2В |
|
| 88 | |||
|
|
|
|
|
|
| ||
|
|
|
|
| Для | решения | задачи | 234 |
|
|
|
|
| недостаточно данных |
|
| |
Напряжение источника | сети | переменного | тока 230В, | а) 10В; б) определить нельзя | 117 | |||
напряжение на зажимах потребителя 220В. Определить: а) |
|
|
|
| ||||
потерю напряжения; б) падение напряжения |
| а) Определить нельзя; |
| 206 | ||||
|
|
|
|
| б) 10В |
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
| а) 10В; б) 10В |
| 8 | |
Активное сопротивление одного провода двухпроводной | 0,5В |
|
| 240 | ||||
линии | переменного | тока | 0,05Ом. | Реактивным |
|
|
|
|
1В |
|
| 46 | |||||
сопротивлением пренебречь. Через нагрузку течет ток 10А. |
|
|
|
| ||||
2В |
|
| 122 | |||||
Найти потерю напряжения |
|
|
|
|
|
| ||
|
| Для | решения | задачи | 83 | |||
|
|
|
|
| ||||
|
|
|
|
| недостаточно данных |
|
| |
|
|
|
|
| ||||
В условиях предыдущей задачи сдвиг фаз между током и | 0,5В |
|
| 155 | ||||
напряжением равен 60°. Определить потерю напряжения |
|
|
|
| ||||
1В |
|
| 112 | |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2В |
|
| 128 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Для | решения | задачи | 2 |
|
|
|
|
| недостаточно данных |
|
| |
§12.5. Расчет проводов по допустимой потере напряжения в линиях постоянного, однофазного и трехфазного тока
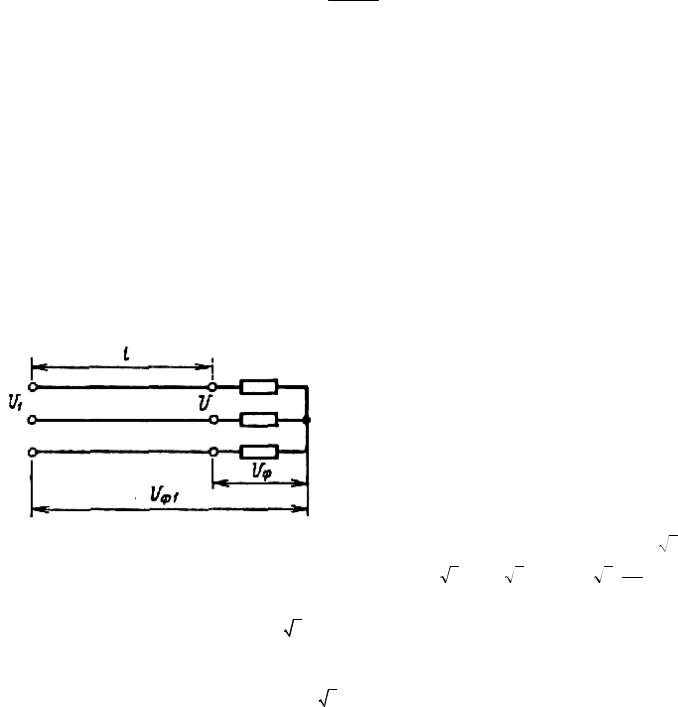
Схема цепи постоянного тока изображена на рис. 12.7. Выразим потерю напряжения через ток в линии и сопротивление проводов:
DU=Ul-U=IRnp.
Рис. 12.7. Схема сети постоянного тока | Рис. 12.8. Схема сети однофазного переменного тока |
Сопротивление проводов |
|
Rпр=2l/(δS), где l — длина линии, м; S — площадь поперечного сечения провода, мм2; δ — удельная электропроводность материала провода, м/(Ом×мм2).
Для меди δм=53м/(Ом×мм2), для алюминия δа=32м/(Ом×мм2). Поскольку линия двухпроводная, то в формулу введен коэффициент 2.
Таким образом,
DU=I2l/(δS), откуда S =I2l/(δΔU).
Для удобства расчетов последнюю формулу преобразуют, для чего числитель и знаменатель умножают на напряжение U:
S = 2Il U = 2lP δDU U δDUU
Здесь потеря напряжения DU выражена в вольтах. Кроме того, в формулу вводят процентную потерю напряжения. В результате получают
S = 200lP δDUU 2
где S — в мм; l — в м; Р — в Вт, U — в В; DU— в %.
На рис. 12.8 изображена электрическая цепь однофазного тока. Реактивное сопротивление линии не учитываем. Согласно § 12.4, DU=IRпpcosj.
Введем процентную потерю напряжения: |
|
|
|
|
|
| ||
| DUU | = | I 2l | cosϕ |
|
|
| |
| 100 |
|
|
|
| |||
Отсюда |
| δ S |
|
|
| |||
2Il cosϕ ×100 |
|
|
| |||||
S = |
|
|
| |||||
где DU — в %. | δDUU |
|
|
| ||||
|
|
|
| 200lUI cosϕ |
| 200lP | ||
Умножив числитель и знаменательна U, получим S = | = | |||||||
δDUU 2 | δDUU 2 | |||||||
|
|
|
|
|
| |||
где Р=UIcosj — активная мощность потребителя.
На рис. 12.9 изображена трехфазная цепь переменного тока с симметричной нагрузкой, для
которой DUф= Uф1-Uф=IR1cosj,
где I — линейный ток; R1=l/(δS) — сопротивление одного провода трехпроводной линии.
Рис. 12.9. Схемы трехфазной сети переменного тока
В справочных таблицах обычно указывается потеря линейного напряжения, которая в 
 3
3
раз больше потери фазного напряжения. Таким образом, DU = 
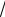 3DUф =
3DUф = 
 3IR1 cosϕ =
3IR1 cosϕ = 
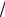 3I δlS cosϕ
3I δlS cosϕ
Следовательно,
| S = | 100l | 3 | I cosϕ , | где DU – в % |
| ||||
|
|
| DUδU |
| линейное напряжение U, | |||||
Умножив числитель и знаменатель последнего выражения на | ||||||||||
окончательно найдем S = | 100lP | , | где | P= |
| UI cosϕ | — активная | мощность, потребляемая | ||
3 | ||||||||||
| ||||||||||
| δDUU 2 |
|
|
|
|
|
|
| ||
симметричной трехфазной нагрузкой. |
|
|
|
|
|
| ||||
Потеря напряжения — это… Что такое Потеря напряжения?
- Потеря напряжения
- – величина, равная разности между установившимися значениями напряжения, измеренными в двух точках системы электроснабжения.
ГОСТ 23875—88.
Коммерческая электроэнергетика. Словарь-справочник. — М.: Энас. В.В. Красник. 2006.
- Потери электроэнергии в электрических сетях
- Потеря связи
Смотреть что такое «Потеря напряжения» в других словарях:
потеря напряжения — — [В.А.Семенов. Англо русский словарь по релейной защите] Тематики релейная защита EN loss of voltage … Справочник технического переводчика
потеря напряжения — įtampos išnykimas statusas T sritis radioelektronika atitikmenys: angl. voltage disappearance; voltage loss vok. Spannungsausfall, m rus. исчезновение напряжения, n; потеря напряжения, f pranc. disparition de tension, f … Radioelektronikos terminų žodynas
потеря напряжения — Разность модулей напряжения по концам элемента электрической системы … Политехнический терминологический толковый словарь
потеря напряжения в системе электроснабжения — Величина, равная разности между установившимися значениями действующего напряжения, измеренными в двух точках системы электроснабжения. [ГОСТ 23875 88] Тематики качество электрической энергииэлектромагнитная совместимость Синонимы потеря… … Справочник технического переводчика
потеря напряжения в линии — Разность между значениями напряжения, измеренными в двух точках электрической линии в данный момент времени. [ОСТ 45.55 99] Тематики электроснабжение в целом … Справочник технического переводчика
потеря напряжения в системе электроснабжения — 3.1.27 потеря напряжения в системе электроснабжения (потеря напряжения): Величина, равная разности между установившимися значениями действующего напряжения, измеренными в двух точках системы электроснабжения. [ГОСТ 23875 88, пункт 27] Источник:… … Словарь-справочник терминов нормативно-технической документации
потеря напряжения в системе электроснабжения UΔ — 44 потеря напряжения в системе электроснабжения UΔ Потеря напряжения: Разность напряжений в начальной и конечной точках электрической линии в данный момент времени de. Verlust der Spannung en. Voltage loss fr. Perte de tension dans le réseau… … Словарь-справочник терминов нормативно-технической документации
Потеря напряжения в системе электроснабжения (Потеря напряжения) — English: Voltage loss Величина, равная разности между установившимися значениями действующего напряжения, измеренными в двух точках системы электроснабжения (по ГОСТ 23875 88) Источник: Термины и определения в электроэнергетике. Справочник … Строительный словарь
наибольшая потеря напряжения электрической сети — Наибольшее из значений суммарной потери напряжения в данной электрической сети … Политехнический терминологический толковый словарь
суммарная потеря напряжения — Сумма потерь напряжения в последовательно включенных элементах электрической системы … Политехнический терминологический толковый словарь
Книги
- Нора Вебстер, Тойбин К.. 1960-е. Ирландия, городок Эннискорти — тот самый, откуда уехала в Америку Эйлиш, героиня предыдущего романа Колма Тойбина «Бруклин» . Тихая, размеренная, старомодная жизнь на фоне назревающей… Подробнее Купить за 417 руб
Потери напряжения в двухпроводной линии
Довольно часто на этапе проектирования возникает необходимость в определении потерь напряжения на линии. Особенно это актуально если линия имеет большую протяженность. В данной статье мы рассмотрим определение потерь напряжения для двухпроводных линий передачи электроэнергии.
Рассмотрим двухпроводную линию с тремя ответвлениями к электроприемникам:

Для определения потерь напряжения в двухпроводной линии постоянного тока достаточно определить потерю напряжения в одном проводе, а полученный результат удвоить.
Двухпроводную схему можно заменить однолинейной:

Где:

Потеря напряжения в двухпроводной линии будет равна разности абсолютных величин напряжения вначале и в конце линии.

Потерю напряжений можно выразить через токи в ответвлениях:

Соответственно:

Подставив выражения токов и длин участков линии в формулу (1) получим выражение для трех ответвлений:

Для случая с количеством ответвлений n:

При расчете электрических сетей определяются потери напряжения при заданном сечении проводов или, наоборот, определяются сечения проводов по допустимой величине потери напряжения. Предположив, что материал и сечение проводов вдоль всей линии одинаковы, получим формулы для определения потери напряжения и сечения проводов в двухпроводной сети постоянного тока:

Потеря напряжения на линии в процентах от номинального:

Где In – ток на n-ом участке , или:

Где In/ — ток в n-ом ответвлении.
Очень часто нагрузка линии задается мощностью электроприемников, подключенных к ней.
По заданным мощностям можно определить токи в ответвлениях, допуская, что напряжение вначале каждого ответвления равно номинальному:

В участках линии:

Потеря напряжения на линии:

Где: Р/ — мощность электроприемников каждого ответвления, Вт; Рn – общая мощность каждого участка линии, Вт; Uн – номинальное напряжение сети, В;
Из формул (5) – (8) по заданной допустимой потере напряжений определяется сечение проводов.
Формулы, полученные для определения потерь в двухпроводной сети постоянного тока, будут справедливы и для однофазных линий переменного тока, при условии, что нагрузка активная (например, только лампы накаливания), а индуктивное и емкостное сопротивление не учитывается.
Что такое потеря напряжения в кабеле и чем она опасна?
Во время передачи электроэнергии по проводам к электроприемникам ее небольшая часть расходуется на сопротивление самих проводов, т.е. на их нагрев. Чем выше протекаемый ток и больше сопротивление провода, тем больше на нем будет потеря напряжения. Величина тока зависит от подключенной нагрузки, а сопротивление провода тем больше, чем больше его длина. Логично? Поэтому нужно понимать, что провода большой длины могут быть не пригодны для подключения какой-либо нагрузки, которая, в свою очередь, хорошо будет работать при коротких проводах того же сечения.
В идеале все электроприборы будут работать в нормальном режиме, если к ним подается то напряжение, на которые они рассчитаны. Если провод рассчитан не правильно и в нем присутствуют большие потери, то на вводе в электрооборудование будет заниженное напряжение. Это очень актуально при электропитании постоянным током, так как тут напряжение очень низкое, например 12 В, и потеря в 1-2 В тут будет уже существенной.
Чем опасна потеря напряжения в электропроводке?
- Отказом работы электроприборов при очень низком напряжении на входе.
В выборе кабеля необходимо найти золотую середину. Его нужно подобрать так, чтобы сопротивление провода при нужной длине соответствовало конкретному току и исключить лишние денежные затраты. Конечно, можно купить кабель огромного сечения и не считать в нем потери напряжения, но тогда за него придется переплатить. А кто хочет отдавать свои деньги на ветер? Давайте ниже разберемся, как учесть потери напряжения в кабеле при его выборе.
Для того чтобы избежать потерь мощности нам нужно уменьшить сопротивление провода. Мы знаем что, чем больше сечение кабеля, тем меньше его сопротивление. Поэтому эта проблема в длинных линиях решается путем увеличения сечения жил кабеля.
Вспомним физику и перейдем к небольшим формулам и расчетам.
Напряжение на проводе мы можем узнать по следующей формуле, зная его сопротивление (R, Ом) и ток нагрузки (I, А).
U=RI
Сопротивление провода рассчитывается так:
R=рl/S, где
р — удельное сопротивление провода, Ом*мм2/м;
l — длина провода, м;
S — площадь поперечного сечения провода, мм2.
Удельное сопротивления это величина постоянная. Для меди она составляет р=0,0175 Ом*мм2/м, и для алюминия р=0,028 Ом*мм2/м. Значения других металлов нам не нужны, так как провода у нас только с медными или с алюминиевыми жилами.
Приведу небольшой пример расчета для медного провода. Для алюминиевого провода суть расчета будет аналогичной.
Например, мы хотим установить группу розеток в гараже и решили протянуть туда медный кабель от дома длинной 50 м сечением 1,5 мм2. Там будем подключаться нагрузка 3,3 кВт (I=15 А).
Учтите, что ток «бежит» по 2-х жильному кабелю туда и обратно, поэтому «пробегаемое» им расстояние будет в два раза больше длины кабеля (50*2=100 м).
Потеря напряжения в данной линии будет:
U=(рl)/s*I=0,0175*100/1,5*15=17,5 В
Что составляет практически 9% от номинального (входного) значения напряжения.
Значит в розетках будет уже напряжение: 220-17,5=202,5 В. Этого будет маловато для нормальной работы электрооборудования. Также свет может гореть тускло (в пол накала).
На нагрев провода будет выделяться мощность P=UI=17,5*15=262,5 Вт.
Также учтите, что здесь не учтены потери в местах соединения (скрутках), в вилке электроприбора, в контактах розетки. Поэтому реальные потери напряжения будут больше полученных значений.
Давайте повторим данный расчет, но уже для провода сечением 2,5 мм2.
U=(рl)/s*I=0,0175*100/2,5*15=10,5 В или 4,7%.
Теперь повторим данный расчет, но уже для провода сечением 4 мм2.
U=(рl)/s*I=0,0175*100/4*15=6,5 В или 2,9%.
Согласно ПУЭ, отклонения напряжения в линии должны составлять не более 5%.
Поэтому в нашем случае нужно выбирать кабель сечением 2,5 мм2 для нагрузки мощностью 3,3 кВт (15 А), а не 1,5 мм2.
Для постоянного тока такие сечения при указанных длинах использовать нельзя. Допусти, что необходимо запитать электроприбор током 15 А от источника постоянного тока 12 В (например, от аккумулятора или понижающего трансформатора). Используется кабель сечением 2,5 мм2 длинной 50 м.
Потери тут будут 10,5 В. Это значит, что на входе в электроприбор будет присутствовать напряжение 12-10,5=1,5 В. Это бред и ничего работать не будет. Даже кабель сечением 25 мм2 не спасет. Тут выход один — это нужно переносить источник питания ближе к потребителю.
Если ваша розетка находится очень далеко от щитка, то обязательно посчитайте потери напряжения в данной линии.
Не забываем улыбаться:
Звонок мужу в командировку:
— Дорогой, а почему в кране нет воды?
— Понимаешь, мы живем на 22 этаже и давления, которое создает насос возможно недостаточно…
— Милый, а почему газа нет?
— Понимаешь, сейчас зима и давление в магистральном газопроводе вследствие большого разбора несколько понижено…
— Родной, но почему же тогда нет электроэнергии?!
— Пойди заплати за коммуналку, дура!
Потеря напряжения в трехфазной линии с нагрузкой на конце
Рассмотрим трехфазную линию с учетом ее активной и индуктивной нагрузки, подключенной в конце линии, а также ее активно-индуктивного сопротивления.

В случае равномерного распределения нагрузки по фазам, а также при одинаковом сопротивлении проводов потерю напряжения могут определять для одной фазы. Для этого расчета используют фазные напряжения в начале и конце линии.
На рисунке выше приведена однолинейная схема для трехфазной линии электропередач с нагрузкой, сосредоточенной на конце. Обозначим:

Построим векторную диаграмму напряжений и токов для одной фазы данной линии:

Отложим некоторый отрезок Оа, который будет представлять в некотором масштабе вектор фазного напряжения Uф2 в конце линии. Под углом φ к нему отложим вектор тока нагрузки I, предполагая, что cos φ < 1. От точки а параллельно вектору тока I отложим отрезок ab, представляющий падение напряжения IR в активном сопротивлении одной фазы линии. От точки b перпендикулярно отрезку ab отложим отрезок bc, представляющий фазное падение напряжения Ix в индуктивном сопротивлении линии.
Из треугольника abc видно, что отрезок ac представляет собой геометрическую сумму падений напряжения в активном и индуктивном сопротивлениях одной фазы линии, то есть полное падение напряжения Iz, где:

Из диаграммы также видно, что вектор фазного напряжения Uф1 в начале линии определяется суммой Uф2 в конце линии и полного падения напряжения Iz в линии.
Геометрическую разность векторов напряжений в начале и конце линий называют падением напряжения:

Из диаграммы следует, что вектор напряжения в конце линии сдвинут относительно вектора напряжения в начале линии на угол:

Для электроприемников важна абсолютная величина напряжения на их зажимах, а не его фаза. Поэтому при расчете электрических сетей определяют потерю U в линии, которая представляет собой алгебраическую разность абсолютных величин напряжений в начале и в конце линии.
Величину потерь U можно определить как разность показаний вольтметров вначале и конце линии электропередач.
На диаграмме потеря напряжения U изображается как отрезок:

Для упрощения расчётов за величину потери ΔUф принимают отрезок af, который является проекцией вектора ΔUф на направление вектора Uф2. Ошибка, получающаяся при этом допущении, не превосходит 3%. Численную величину потерь U можно определить, сложив отрезки ad и af, выраженные в масштабе напряжений.
Графически это выглядит так:

Следовательно:

Зная, что линейная потеря напряжения составит:

Получим формулу для определения потери U в трехфазной линии с нагрузкой на конце:

Если нагрузка в конце линии задается не током, а мощностью, то получим:

Подставив это выражение в формулу потерь:

После незначительных преобразований:

Пример
Определить потерю напряжения в трехфазной воздушной линии с Uном = 6 кВ протяженностью 1,5 км питающей насосную станцию мощностью 100 кВт с cos φ = 0,8; tg φ = 0,75. Линия выполнена стальными многопроволочными проводами марки ПС-25.
Решение
Ток нагрузки будет равен:

Определяем сопротивления. r0 = 5,7 Ом/км и внутреннее индуктивное сопротивление x0 = 1,2 Ом/км.
Внешнее индуктивное сопротивление x0/ = 0,4 Ом/км.
Полное индуктивное сопротивление

Потеря напряжения:

